PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
|
|
|
- Alfonso Giménez Serrano
- hace 5 años
- Vistas:
Transcripción
1 I.E.S. CASTELAR BADAJOZ A. Menguiano PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE - 8 (RESUELTOS por Anonio Menguiano) MATEMÁTICAS II Tiempo máimo: horas minuos Se valorará la corrección la claridad en el lenguaje (maemáico o no maemáico) empleado por el alumno. Penalian los errores de cálculo. Los errores graves, especialmene, aquellos que lleven a resulados incoherenes o absurdos, serán penaliados con la aplicación del 5 % sobre la caliicación en cuesión. Se valorarán odas las pares que sean correcas, aunque el resulado inal no lo sea. Conesa de manera clara raonada una de las dos opciones propuesas. Cada cuesión se punúa sobre punos. La caliicación inal se obiene de dividir el oal enre. OPCIÓN A º) Deermina odas las marices de la orma que conmuen ( A A ) con la mari A. A A Las marices son de la orma R,
2 º) Deermina el puno A del plano más próimo al puno P(,, ). El ha de recas paralelas perpendiculares al plano ienen como vecor direcor al vecor normal del plano, que es,, n. De las ininias recas del ha anerior, la que pasa por P es r. La solución es el puno Q de inersección del plano con la reca r es:,, Q r
3 º) Se considera la unción a ) Calcular. b ) Calcular los eremos relaivos. c ) Hacer un dibujo de la unción.. Se pide: a ) In de. In de. b ) Para esudiar los eremos relaivos, derivamos: ( ) ( ) ( ) ( ) ( ) Para que una unción engo un máimo o un mínimo relaivo es condición necesaria que se anule la primera derivada: ( ). Para dierenciar los máimos de los mínimos recurrimos a la segunda derivada: si es negaiva para los valores que anulan la primera derivada se raa de un máimo, en caso conrario de un mínimo: ( ) ( ) ( ) ( ) ( ) ( ) ( )
4 [ ] [ ] 8 > para Mínimo, : P relaivo Mínimo 8 < para Máimo, : Q relaivo Máimo Observación: El máimo relaivo se podía haber obenido eniendo en cuena que la unción es simérica con respeco al origen por cumplir que () - (-). c ) Teniendo en cuena que el eje es asínoa de la unción, según se demuesra en el aparado a ), la represación gráica, aproimada, es la que aparece en el gráico adjuno. Y () O P Q
5 º) a ) Se considera la curva e, >. Escribe la ecuación de la unción A() que nos da el área de la región limiada por esa curva las recas,. b ) Hacer un dibujo de la siuación. c ) Calcula A( ). a ) La curva e iene odas sus ordenadas posiivas, por lo cual, el área en unción de viene epresada por la siguiene inegral deinida: e d e d [ e ] ( e e ) A d d e ( e ) A( ) b ) Teniendo en cuena que se raa de una unción eponencial de base posiiva es monóona creciene su recorrido es (, ), por ser e, siendo >, el eje de abscisas es asínoa horional de la curva. Cora al eje de ordenadas en el puno A(, ). La represenación gráica de la siuación es la de la igura: Y () e A O
6 c ) { } L Hopial er Ins e e A. de e e
7 OPCIÓN B º) Demuesra, para marices de dimensión, que el deerminane de un produco de marices es el deerminane del produco de las marices. Es ciero que el deerminane de una suma de marices es la suma de los deerminanes de las marices? Sean las marices a b A c d p. Su produco es: a b a b a bp A. c d p c d c dp El deerminane del produco es el siguiene: A a b c d a bp c dp ( a b)( c dp) ( a bp)( c d) ac adp bc bdp ac ad bcp bdp adp bc ad bcp A Los valores de los deerminanes de las marices son: a b A ad bc A p c d p El produco de los deerminanes es el siguiene: A ( ad bc)( p ) adp ad bcp bc A A B A como se pedía demosrar. Veamos si se cumple que A A : A a c b d a p c b d p A a c b d p ( a )( d p) ( b )( c ) ad ap d p bc b c A
8 a b A ad bc p A c d p A B A como se ha demosrado.
9 º) Deermina un puno de la reca r,,,,,, más próimo al puno P(,, ). El ha de planos perpendiculares a la reca r,,,,,, ienen como vecor normal al vecor direcor de r que es,, n. El ha de planos iene por ecuación general D α. De ls ininias planos del ha anerior, el que coniene al puno P(,, ) iene que saisacer su ecuación:,, D D P D α. La solución es el puno Q de core de la reca r el plano, que es el siguiene: La epresión de r por unas ecuaciones paraméricas es r.,, 7 9 Q r
10 º) Se considera la unción. Se pide: a ) Calcular ;. b ) Calcular los eremos relaivos. c ) Hacer un dibujo de la unción. a ) La unción carece de ie para. de. In de. In b ) Para esudiar los máimos mínimos relaivos calculamos sus derivadas primera segunda:
11 ( ) ( ) Para que eisan máimos o mínimos relaivos es condición necesaria que se anule la primera derivada: ( ) ( ) ( ) ( ) < Má. Má. O(, ) ( ) > Mín. Mín. P(, ) c ) Con objeo de aciliar el dibujo de la unción, vamos a deerminar sus asínoas, que son las siguienes: Horionales: son los valores inios que oma la unción cuando iende a valer ininio; son de la orma. Del primer aparado sabemos que, de donde se deduce que la unción no iene asínoas horionales. Vericales: son los valores de que anulan el denominador: Oblicuas: Para que una unción racional enga asínoas oblicuas es necesario que el grado del numerador sea una unidad maor que el grado del denominador; como en nuesro caso ocurre eso, iene asínoas oblicuas. m m n [ m] n Asínoa oblícua Con los daos aneriores, la represenación gráica de la unción es, aproimadamene, la siguiene:
12 Y () P O
13 º) Dibuja la región limiada por las curas sen, cos, las recas. Calculad el área del recino. Las gráicas de las unciones seno coseno se dierencian en que ienen un desase de (9º). (La palabra coseno se deriva de complemeno del seno) Se raa de dos unciones coninuas cuo dominio es R el recorrido de ambas es. [-, ]; el periodo de ambas es Teniendo en cuena que el coseno de un ángulo es igual al seno del ángulo complemenario, las gráicas de las unciones seno coseno son las que se indican a coninuación, epresadas en el inervalo de un giro. Como puede observarse, en el inervalo comprendido por las dos recas vericales, las ordenadas de la curva cos son maores que las de cos en el inervalo comprendido enre las recas vericales son maores las ordenadas de sen que las de cos, por lo cual el área pedida es la siguiene: ( cos sen ) d ( sen cos ) d [ sen cos ] [ cos sen ] S / / sen cos S ( sen cos ) ( cos sen ) cos sen / / / / - cos sen sen cos sen cos cos sen cos sen u S
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho
 IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO 2011 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
C cos x sen x 0 x sen x x cos x x sen x cos x x C 1 x 0. Calculamos la matriz adjunta de C: sen x 0 cox 0 cos x sen x. sen x x 1 x 1 sen x
 Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
EXAMEN DE MATEMÁTICAS I 8 de febrero de 2006
 EXAMEN DE MATEMÁTICAS I 8 de febrero de 006 MATEMÁTICAS I Eamen del º PARCIAL 8 de febrero de 006 Sólo una respuesa a cada cuesión es correca. Respuesa correca: 0. punos. Respuesa incorreca: -0. punos
EXAMEN DE MATEMÁTICAS I 8 de febrero de 006 MATEMÁTICAS I Eamen del º PARCIAL 8 de febrero de 006 Sólo una respuesa a cada cuesión es correca. Respuesa correca: 0. punos. Respuesa incorreca: -0. punos
El sistema es incompatible. b) El sistema es compatible determinado. Lo resolvemos por la regla de Cramer.
 Prueba de Acceso a la Universidad. JUNIO 0. Maemáicas II. El alumno debe responder a una de las dos opciones propuesas, A o B. En cada preguna se señala la punuación máima. OPCIÓN A a y z A. Sean a un
Prueba de Acceso a la Universidad. JUNIO 0. Maemáicas II. El alumno debe responder a una de las dos opciones propuesas, A o B. En cada preguna se señala la punuación máima. OPCIÓN A a y z A. Sean a un
Geometría del espacio
 Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
MATEMÁTICAS II. x x x d) ( ) b) Como el grado del numerador y del denominador son iguales, hay que empezar por hacer la división.
 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Ejercicio Calcula la siguienes inegrales a) d b) d c) 6 d d) 3 d e) d 9 e a) Haciendo el cambio de variable d d. d d d
Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Ejercicio Calcula la siguienes inegrales a) d b) d c) 6 d d) 3 d e) d 9 e a) Haciendo el cambio de variable d d. d d d
MATEMÁTICAS II TEMA 5 Ecuaciones de rectas y planos en el espacio. Posiciones relativas Problemas propuestos
 Geomería del espacio ecuaciones de recas planos; posiciones relaivas MATEMÁTICAS II TEMA Ecuaciones de recas planos en el espacio. Posiciones relaivas Problemas propuesos Ecuaciones de recas planos. Halla,
Geomería del espacio ecuaciones de recas planos; posiciones relaivas MATEMÁTICAS II TEMA Ecuaciones de recas planos en el espacio. Posiciones relaivas Problemas propuesos Ecuaciones de recas planos. Halla,
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO 2010 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 ES CSTELR DJOZ Menguiano PRUE DE CCESO (LOGSE) UNVERSDD DE LERES JUNO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTCS Tiepo áio: horas inuos Conese de anera clara raonada una de las dos opciones propuesas
ES CSTELR DJOZ Menguiano PRUE DE CCESO (LOGSE) UNVERSDD DE LERES JUNO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTCS Tiepo áio: horas inuos Conese de anera clara raonada una de las dos opciones propuesas
. Podemos afirmar: Dom f. c) f es creciente en un entorno de x 0. = y(t) 9.- Sean las ecuaciones paramétricas de una curva plana.
 1.- Sea una función coninua y = f() al que el dominio de f() =[a,b], enonces: a) El máimo absoluo de f() se alcanza en uno de los valores ales que f ()=0. b) No iene porque ener máimo absoluo. c) El máimo
1.- Sea una función coninua y = f() al que el dominio de f() =[a,b], enonces: a) El máimo absoluo de f() se alcanza en uno de los valores ales que f ()=0. b) No iene porque ener máimo absoluo. c) El máimo
OPCIÓN A MATEMÁTICAS 2º BACHILLERATO B
 MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN 2013
 GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
Opción A Ejercicio 1.-
 Soluciones modelo (Sepiembre de 009) Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f( ) -+. Deermina la asínoa de la gráfica Evidenemene, la función no iene asínoas vericales,
Soluciones modelo (Sepiembre de 009) Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f( ) -+. Deermina la asínoa de la gráfica Evidenemene, la función no iene asínoas vericales,
5. Planos y rectas en el espacio
 5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
45 EJERCICIOS de INTEGRAL DEFINIDA 2º BACH. ( )
 5 EJERCICIOS de INTEGRAL DEFINIDA º BACH. Inegral definida:. Enunciar la regla de Barrow. Calcular:. Calcular:. (S) Calcular: d (Soluc: ) a + b a ( ) a + b d Soluc : b d (Soluc: 5/). Calcular: 5. Calcular:
5 EJERCICIOS de INTEGRAL DEFINIDA º BACH. Inegral definida:. Enunciar la regla de Barrow. Calcular:. Calcular:. (S) Calcular: d (Soluc: ) a + b a ( ) a + b d Soluc : b d (Soluc: 5/). Calcular: 5. Calcular:
DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =
![DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función = DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =](/thumbs/52/30419199.jpg) DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 3: ESPACIO AFÍN Y EUCLÍDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 00 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 00 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
a) en [0, 2] ; b) en [-1, 1]
![a) en [0, 2] ; b) en [-1, 1] a) en [0, 2] ; b) en [-1, 1]](/thumbs/80/82443407.jpg) UNIVERSIDAD NACIONAL DE LA PATAGONIA SAN JUAN BOSCO FACULTAD DE CIENCIAS NATURALES CATEDRA: Maemáica I CURSO: 04 TRABAJO PRACTICO Nº -Tercera Pare Pare III. Aplicaciones de la derivada TEOREMA DE ROLLE
UNIVERSIDAD NACIONAL DE LA PATAGONIA SAN JUAN BOSCO FACULTAD DE CIENCIAS NATURALES CATEDRA: Maemáica I CURSO: 04 TRABAJO PRACTICO Nº -Tercera Pare Pare III. Aplicaciones de la derivada TEOREMA DE ROLLE
Examen de Matemáticas II 2º de Bachillerato
 º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
1 a 1 a 1. 0 a 1 a a 0. 0 a 1 a 1 a a 1 a 1 a 1 a 1 a a 1 a 1 a 1 a 1. a 1 a 1 a 1 a 1 0 a 1, a 1
 Pruebas de Apiud para el Acceso a la Universidad. JUNIO 1998. Maemáicas II. OPCIÓN A 1. Discuir el sisema a z solución del mismo cuando a = [1 puno] (a 1) y a z 1 (a 1) y (a 1) z según sea el valor del
Pruebas de Apiud para el Acceso a la Universidad. JUNIO 1998. Maemáicas II. OPCIÓN A 1. Discuir el sisema a z solución del mismo cuando a = [1 puno] (a 1) y a z 1 (a 1) y (a 1) z según sea el valor del
Opción A Ejercicio 1.-
 Colegio Lux Mundi (Cajar-Granada) Examen Sepiembre de 009 Javier Cosillo Iciarra Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f ( x ) x -x+x. Deermina la asínoa de la
Colegio Lux Mundi (Cajar-Granada) Examen Sepiembre de 009 Javier Cosillo Iciarra Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f ( x ) x -x+x. Deermina la asínoa de la
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 3: ESPACIO AFÍN Y EUCLÍDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
GUÍA DE EJERCICIOS II
 Faculad de Ingeniería UCV Álgebra ineal Geomería Analíica Ciclo Básico GUÍA DE Encuenre las ecuaciones de la reca que a) iene vecor direcor v (,, ) pasa por el puno P ( 4, 5, ) b) pasa por los punos A
Faculad de Ingeniería UCV Álgebra ineal Geomería Analíica Ciclo Básico GUÍA DE Encuenre las ecuaciones de la reca que a) iene vecor direcor v (,, ) pasa por el puno P ( 4, 5, ) b) pasa por los punos A
Tema 12. Problemas Métricos. Raúl González Medina. I.E. Juan Ramón Jiménez Tema 12
 Tema Problemas Méricos.- Inroducción..- Disancias...- Enre dos punos..- Enre puno y reca...- Enre puno y plano...- Enre dos recas..5.- Enre reca y plano..6.- Enre dos planos..- Ángulos..- Enre dos recas...-
Tema Problemas Méricos.- Inroducción..- Disancias...- Enre dos punos..- Enre puno y reca...- Enre puno y plano...- Enre dos recas..5.- Enre reca y plano..6.- Enre dos planos..- Ángulos..- Enre dos recas...-
EXAMEN DE MATEMÁTICAS I (Primer Parcial) 11 de febrero de 2009
 EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
(a-3)x+(a-2)y+2z=-1 (2a-6)x+(3a-6)y+5z=-1 (3-a)x+(a-2)z=a 2-4a+5. a-3. a 2-4a a 2-4a+3
 EXTRAORDINARIO DE 8. PROBLEMA A. Esudia el siguiene sisema de ecuaciones lineales dependiene del parámero real a y resuélvelo en los casos en que es compaible: Aplicamos el méodo de Gauss: a-3 (a-3) 3-a
EXTRAORDINARIO DE 8. PROBLEMA A. Esudia el siguiene sisema de ecuaciones lineales dependiene del parámero real a y resuélvelo en los casos en que es compaible: Aplicamos el méodo de Gauss: a-3 (a-3) 3-a
MODELO JUNIO 2005 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
 Modelo de eamen Junio MODELO JUNIO MTEMÁTICS PLICDS LS CIENCIS SOCILES II OPCIÓN. (Punuación máima: punos) Se dice que una mari cuadrada es orogonal si T I: Noa: La noación T significa mari ranspuesa de.
Modelo de eamen Junio MODELO JUNIO MTEMÁTICS PLICDS LS CIENCIS SOCILES II OPCIÓN. (Punuación máima: punos) Se dice que una mari cuadrada es orogonal si T I: Noa: La noación T significa mari ranspuesa de.
REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA
 Represenación de curvas planas dadas en forma paramérica REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA PLANTEAMIENTO DEL PROBLEMA Sean x e y dos funciones reales de variable real, de dominios
Represenación de curvas planas dadas en forma paramérica REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA PLANTEAMIENTO DEL PROBLEMA Sean x e y dos funciones reales de variable real, de dominios
Unidad 5 Geometría afín en el espacio
 Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2015
 GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
Actividades de recuperación
 Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE LAS PALMAS JUNIO 2012 (GENERAL) Tiempo máximo: 1 horas y 30 minutos
 ES STELR DJOZ PRUE DE ESO (LOGSE) UNVERSDD DE LS PLS JUNO (GENERL) TEÁTS Tiepo áio: horas inuos Elija una de las dos opciones, o, conese a las cuaro pregunas que coponen la opción elegida Si ecla pregunas
ES STELR DJOZ PRUE DE ESO (LOGSE) UNVERSDD DE LS PLS JUNO (GENERL) TEÁTS Tiepo áio: horas inuos Elija una de las dos opciones, o, conese a las cuaro pregunas que coponen la opción elegida Si ecla pregunas
GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA
 GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA Una curva C se dice definida paraméricamene por medio de un parámero, si las coordenadas afines de sus punos M se expresan en función de ese parámero, cuando varía
GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA Una curva C se dice definida paraméricamene por medio de un parámero, si las coordenadas afines de sus punos M se expresan en función de ese parámero, cuando varía
( ) ( 15 50) 0
 PRUE DE CCESO L UNIVERSIDD JUNIO 7 OPCION ) Deermina dos números reales posiivos sabiendo que su suma es y que el produco de sus cuadrados es máximo. Sean x e y los números reales que suman y P x y odos
PRUE DE CCESO L UNIVERSIDD JUNIO 7 OPCION ) Deermina dos números reales posiivos sabiendo que su suma es y que el produco de sus cuadrados es máximo. Sean x e y los números reales que suman y P x y odos
Unidad 9 Funciones exponenciales, logarítmicas y trigonométricas
 Unidad 9 Funciones eponenciales, logarímicas y rigonoméricas PÁGINA 177 SOLUCIONES 1. En cada uno de los res casos: a) Domf = Imf = Esricamene creciene en odo su dominio. No acoada. Simérica respeco al
Unidad 9 Funciones eponenciales, logarímicas y rigonoméricas PÁGINA 177 SOLUCIONES 1. En cada uno de los res casos: a) Domf = Imf = Esricamene creciene en odo su dominio. No acoada. Simérica respeco al
1. Derivadas de funciones de una variable. Recta tangente.
 1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 I.E.S. ASTELAR BADAJOZ A. enguiano PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO - 8 (RESUELTOS por Antonio enguiano) ATEÁTIAS II Tiepo áio: horas inutos Se valorará la corrección la claridad en
I.E.S. ASTELAR BADAJOZ A. enguiano PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO - 8 (RESUELTOS por Antonio enguiano) ATEÁTIAS II Tiepo áio: horas inutos Se valorará la corrección la claridad en
MATEMÁTICAS II. ANDALUCÍA Pruebas de acceso a la Universidad SOLUCIONES 1. (2001-1A-3) Tienen inversa las matrices A y D.
 MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
Propuesta A. 1. Dadas las matrices: C = B = A =
 Pruebas de Acceso a Enseñanzas Univerarias Oiciales de Grado 6 Maeria: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá conesar a una de las dos opciones propuesas A ób. Se podrá uilizar
Pruebas de Acceso a Enseñanzas Univerarias Oiciales de Grado 6 Maeria: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá conesar a una de las dos opciones propuesas A ób. Se podrá uilizar
TEMA 47. GENERACIÓN DE CURVAS POR ENVOLVENTES
 Tema 47. Generación de curvas por envolvenes. TEMA 47. GENERACIÓN DE CURVAS POR ENVOLVENTES. Inroducción. Una curva o supericie es envolvene de un conjuno de curvas o supericies si es angene en cada puno
Tema 47. Generación de curvas por envolvenes. TEMA 47. GENERACIÓN DE CURVAS POR ENVOLVENTES. Inroducción. Una curva o supericie es envolvene de un conjuno de curvas o supericies si es angene en cada puno
Cálculo Diferencial e Integral - Funciones trascendentales. Prof. Farith J. Briceño N.
 Cálculo Diferencial e Inegral - Funciones rascenenales. Prof. Farih J. Briceño N. Objeivos a cubrir Función logarimo y eponencial. Propieaes. Derivaa e inegración. Cóigo : MAT-CDI.5 Ejercicios resuelos
Cálculo Diferencial e Inegral - Funciones rascenenales. Prof. Farih J. Briceño N. Objeivos a cubrir Función logarimo y eponencial. Propieaes. Derivaa e inegración. Cóigo : MAT-CDI.5 Ejercicios resuelos
TRABAJO PRÁCTICO N 3: Derivadas - Diferencial
 TRABAJO PRÁCTICO N : Derivadas - Diferencial ) Definición de derivada en un puno: La derivada de la función f es aquella función, denoada por f ', al que su valor en un número del dominio de f esá dado
TRABAJO PRÁCTICO N : Derivadas - Diferencial ) Definición de derivada en un puno: La derivada de la función f es aquella función, denoada por f ', al que su valor en un número del dominio de f esá dado
ANDALUCÍA JUNIO 2004
 ANDALUCÍA JUNIO 004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Insrucciones: a) Duración: 1 hora y 0 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida.
ANDALUCÍA JUNIO 004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Insrucciones: a) Duración: 1 hora y 0 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida.
Examen Final de Ecuaciones Diferenciales Septiembre 2007
 Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
March 2, 2009 CAPÍTULO 3: DERIVADAS PARCIALES Y DIFERENCIACIÓN
 March 2, 2009 1. Derivadas Parciales y Funciones Diferenciables En ese capíulo, D denoa un subconjuno abiero de R n. Definición 1.1. Consideremos una función f : D R y sea p D, i = 1,, n. Definimos la
March 2, 2009 1. Derivadas Parciales y Funciones Diferenciables En ese capíulo, D denoa un subconjuno abiero de R n. Definición 1.1. Consideremos una función f : D R y sea p D, i = 1,, n. Definimos la
CAPITULO 7.FUNCIONES DE VARIAS VARIABLES Campo de definición de una función de varias variables.
 CAPITULO 7.FUNCIONES DE VARIAS VARIABLES Deinición Sean E F dos conjunos inios o ininios de cualquier nauralea. Una aplicaron del conjuno E en el conjuno F es una le o proceso mediane el cual se hace corresponder
CAPITULO 7.FUNCIONES DE VARIAS VARIABLES Deinición Sean E F dos conjunos inios o ininios de cualquier nauralea. Una aplicaron del conjuno E en el conjuno F es una le o proceso mediane el cual se hace corresponder
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-V--00-208 CURSO: Maemáica Inermedia CÓDIGO DEL CURSO: 07 SEMESTRE: Primer Semesre JORNADA: Vesperina
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-V--00-208 CURSO: Maemáica Inermedia CÓDIGO DEL CURSO: 07 SEMESTRE: Primer Semesre JORNADA: Vesperina
x t, x t, x dx dt sustituyendo e integrando, obtenemos: 3
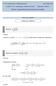 E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE)
 UNIVERSIDADES PÚBLICAS DE LA COUNIDAD DE ADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 8-9 (Sepiebre) ATERIA: ATEÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El aluno conesará a los
UNIVERSIDADES PÚBLICAS DE LA COUNIDAD DE ADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 8-9 (Sepiebre) ATERIA: ATEÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El aluno conesará a los
Modelo 2 OPCIÓN A. A y B AB se puede realizar porqueel n decolumnas de Aesigual al n de filas de B AB. t t t
 Insrucciones: a) Duración: 1 hora y 3 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida. c) En cada ejercicio, pare o aparado se indica la punuación máxima
Insrucciones: a) Duración: 1 hora y 3 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida. c) En cada ejercicio, pare o aparado se indica la punuación máxima
DESCRIPCIÓN MATEMÁTICA DE LAS ONDAS VIAJERAS
 DESCRIPCIÓN MAEMÁICA DE LAS ONDAS VIAJERAS Ecuación de onda de la orma Signo - = Espacio ( x ± v ) iempo El argumeno de la unción se denomina ase de la onda. Para que sea una onda viajera en la ase siempre
DESCRIPCIÓN MAEMÁICA DE LAS ONDAS VIAJERAS Ecuación de onda de la orma Signo - = Espacio ( x ± v ) iempo El argumeno de la unción se denomina ase de la onda. Para que sea una onda viajera en la ase siempre
{ } n 2 n n. n n n n. n n 3 n. a b c. A = = ; calcular el valor de 2, 2 t t. a Calcular el siguiente determinante de orden n:
 EJERCICIOS. PLICCIONES DE LOS DETERMINNTES.. Calcular el siguiene deerminane de orden n: n n n n n n n n n n n n n. Demosrar que si es una mariz al que n n, se verifica lo anerior? =, enonces. Y si es
EJERCICIOS. PLICCIONES DE LOS DETERMINNTES.. Calcular el siguiene deerminane de orden n: n n n n n n n n n n n n n. Demosrar que si es una mariz al que n n, se verifica lo anerior? =, enonces. Y si es
UNIVERSIDAD DE LA RIOJA PRUEBA DE ACCESO (LOGSE) MATEMÁTICAS II JUNIO 2011 (GENERAL) Solución
 IES CASTELAR BADAJOZ Junio de (General) Soluciones Antonio Mengiano Corbacho UNIVERSIDAD DE LA RIOJA PRUEBA DE ACCESO (LOGSE) MATEMÁTICAS II JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas minutos El
IES CASTELAR BADAJOZ Junio de (General) Soluciones Antonio Mengiano Corbacho UNIVERSIDAD DE LA RIOJA PRUEBA DE ACCESO (LOGSE) MATEMÁTICAS II JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas minutos El
Ecuaciones de primer orden
 Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE CANTABRIA SEPTIEMBRE (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR JOZ PRUE E CCESO (LOGSE) UNIVERSI E CNTRI SEPTIEMRE - 9 (RESUELTOS or nonio Menguiano) MTEMÁTICS II Tieo áio: horas inuos - ebe escogerse una sola de las ociones - ebe eonerse con claridad el
IES CSTELR JOZ PRUE E CCESO (LOGSE) UNIVERSI E CNTRI SEPTIEMRE - 9 (RESUELTOS or nonio Menguiano) MTEMÁTICS II Tieo áio: horas inuos - ebe escogerse una sola de las ociones - ebe eonerse con claridad el
{ 3} Nota. La raíz no impone condiciones al dominio por ser de índice impar.
 . Esudia el dominio de las siguienes unciones: a ( : Función Racional, el dominio son odos los números reales ecepo los que anulen el denominador. R / 0 : 0 : : ± [ ( ] { } R ± { } b ( : Función Racional,
. Esudia el dominio de las siguienes unciones: a ( : Función Racional, el dominio son odos los números reales ecepo los que anulen el denominador. R / 0 : 0 : : ± [ ( ] { } R ± { } b ( : Función Racional,
= A, entonces A = 0. Y si A es una matriz. y comprobar el resultado. ,, ;,, es el mismo que el generado
 EJERCICIOS. APLICACIONES DE LOS DETERMINANTES. 1. Calcular el siguiene deerminane de orden n: 1 n n n n n n n n n n n n n. Demosrar que si A es una mariz al que n n, se verifica lo anerior? A = A, enonces
EJERCICIOS. APLICACIONES DE LOS DETERMINANTES. 1. Calcular el siguiene deerminane de orden n: 1 n n n n n n n n n n n n n. Demosrar que si A es una mariz al que n n, se verifica lo anerior? A = A, enonces
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE)
 UNIVERSIDDES PÚLICS DE L COUNIDD DE DRID PRUET DE CCESO ESTUDIOS UNIVERSITRIOS (LOGSE) Curso 8-9 (Sepiebre) TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN El aluno conesará a los cuaro ejercicios de
UNIVERSIDDES PÚLICS DE L COUNIDD DE DRID PRUET DE CCESO ESTUDIOS UNIVERSITRIOS (LOGSE) Curso 8-9 (Sepiebre) TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN El aluno conesará a los cuaro ejercicios de
ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1
 ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1 A) Hallar la pendiene de la reca secane a la parábola y + 8,cuyas abscisas de los punos de inersección son 1 y 4 f ( ) f ( a) B) Dada la siguiene epresión
ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1 A) Hallar la pendiene de la reca secane a la parábola y + 8,cuyas abscisas de los punos de inersección son 1 y 4 f ( ) f ( a) B) Dada la siguiene epresión
Propuesta A. y B = 1 0
 Pruebas de cceso a Enseñanzas Univerarias Oiciales de Grado Maeria: MEMÁIS PLIDS LS IENIS SOILES II El alumno deberá conesar a una de las dos opciones propuesas o. Se podrá uilizar cualquier ipo de calculadora..
Pruebas de cceso a Enseñanzas Univerarias Oiciales de Grado Maeria: MEMÁIS PLIDS LS IENIS SOILES II El alumno deberá conesar a una de las dos opciones propuesas o. Se podrá uilizar cualquier ipo de calculadora..
EJERCICIOS PROPUESTOS
 8 Deerminanes. Ejercicio resuelo. EJERCICIOS PROPUESTOS. Calcula el valor de los siguienes deerminanes. 8 4 5 0 0 6 c) 4 5 4 8 6 4 8 4 5 0 6+ 0 0+ 5 00 5 6 0+ 000 0 48 0 6 ( ) ( ) ( ) ( ) ( ) 4 5 5 + 4
8 Deerminanes. Ejercicio resuelo. EJERCICIOS PROPUESTOS. Calcula el valor de los siguienes deerminanes. 8 4 5 0 0 6 c) 4 5 4 8 6 4 8 4 5 0 6+ 0 0+ 5 00 5 6 0+ 000 0 48 0 6 ( ) ( ) ( ) ( ) ( ) 4 5 5 + 4
MATEMÁTICAS II Examen del 28/05/2012 Solución Importante
 MATEMÁTICAS II Examen del 8/05/0 Solución Imporane Las calificaciones se harán públicas en el aula virual el 08/06/0. La revisión será el /06/0 y el /06/0 de -3 horas en la sala D-4-. MATEMÁTICAS II 8/05/0
MATEMÁTICAS II Examen del 8/05/0 Solución Imporane Las calificaciones se harán públicas en el aula virual el 08/06/0. La revisión será el /06/0 y el /06/0 de -3 horas en la sala D-4-. MATEMÁTICAS II 8/05/0
CAPÍTULO 1 LA FUNCIÓN DERIVADA
 CAPÍTULO LA FUNCIÓN DERIVADA. LA DERIVADA En el fascículo anerior uilizase el concepo de la razón de cambio a ravés de problemas o siuaciones de la vida real e ilusrase gráficamene 0 o, dando una inerpreación
CAPÍTULO LA FUNCIÓN DERIVADA. LA DERIVADA En el fascículo anerior uilizase el concepo de la razón de cambio a ravés de problemas o siuaciones de la vida real e ilusrase gráficamene 0 o, dando una inerpreación
Trabajo Práctico N 0: Curvas planas-ecuaciones paramétricas y Coordenadas polares
 Trabajo Prácico N 0: Curvas planas-ecuaciones paraméricas y Coordenadas polares Curvas planas y ecuaciones paraméricas Hasa ahora hemos represenado una gráfica por medio de una sola ecuación que coniene
Trabajo Prácico N 0: Curvas planas-ecuaciones paraméricas y Coordenadas polares Curvas planas y ecuaciones paraméricas Hasa ahora hemos represenado una gráfica por medio de una sola ecuación que coniene
Ondas y Rotaciones. Principios fundamentales II
 Ondas y Roaciones rincipios fundamenales II Jaime Feliciano Hernández Universidad Auónoma Meropoliana - Izapalapa México, D. F. 5 de agoso de 0 INTRODUCCIÓN. Generalmene el esudio del movimieno se realiza
Ondas y Roaciones rincipios fundamenales II Jaime Feliciano Hernández Universidad Auónoma Meropoliana - Izapalapa México, D. F. 5 de agoso de 0 INTRODUCCIÓN. Generalmene el esudio del movimieno se realiza
Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de varias variables. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C.
 Maemáicas 1 1 EJERCICIOS RESUELTOS: Funciones de varias variables Elena Álvarez Sáiz Dpo. Maemáica Aplicada C. Compuación Universidad de Canabria Ingeniería de Telecomunicación Ejercicios: Func. varias
Maemáicas 1 1 EJERCICIOS RESUELTOS: Funciones de varias variables Elena Álvarez Sáiz Dpo. Maemáica Aplicada C. Compuación Universidad de Canabria Ingeniería de Telecomunicación Ejercicios: Func. varias
a) Dar la definición de dominio y rango de una función. b) Explicar cada una de las siguientes funciones y dar tres ejemplos de cada una.
 UNIVERSIDAD DE LONDRES PREPARATORIA GUIA DE MATEMÁTICAS VI Áreas I-II Plan : 9 Clave maeria : 00 Clave UNAM : Unidad I. Funciones Objeivos Que el alumno idenifique disinos ipos de funciones, esablezca
UNIVERSIDAD DE LONDRES PREPARATORIA GUIA DE MATEMÁTICAS VI Áreas I-II Plan : 9 Clave maeria : 00 Clave UNAM : Unidad I. Funciones Objeivos Que el alumno idenifique disinos ipos de funciones, esablezca
Autoevaluación Cálculo Integral. sen(x) dx (i) cos(x)
 Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES 2.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS
 CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS Hasa ahora conocemos la represenación de una grafica mediane una ecuación con dos variables. En ese
CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS Hasa ahora conocemos la represenación de una grafica mediane una ecuación con dos variables. En ese
Representación gráfica de curvas en forma paramétrica x a(t sent) 1.- Representar la curva dada por
 Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
prepara TU SElECTIVIDAD
 prepara TU SElECTIVIDAD Se considera la función f ( ) = ( + a) e a siendo a un parámero real. a) Razone a qué es igual el dominio de f ( ). b) Deermine el valor de a para que la gráfica de f() pase por
prepara TU SElECTIVIDAD Se considera la función f ( ) = ( + a) e a siendo a un parámero real. a) Razone a qué es igual el dominio de f ( ). b) Deermine el valor de a para que la gráfica de f() pase por
1 Física General I Paralelos 05 y 22. Profesor RodrigoVergara R 0102) Movimiento Rectilíneo Horizontal
 Física General I Paralelos 5 y. Profesor Rodrigoergara R ) Movimieno Recilíneo Horizonal ) Concepos basicos Definir disancia recorrida, posición y cambio de posición. Definir vecores posicion, velocidad
Física General I Paralelos 5 y. Profesor Rodrigoergara R ) Movimieno Recilíneo Horizonal ) Concepos basicos Definir disancia recorrida, posición y cambio de posición. Definir vecores posicion, velocidad
Soluciones a los ejercicios propuestos Unidad 3. Ecuaciones, inecuaciones y sistemas Matemáticas aplicadas a las Ciencias Sociales
 Soluciones a los ejercicios propuesos Unidad cuaciones inecuaciones sisemas Maemáicas aplicadas a las Ciencias Sociales CUACIONS D SGUNDO GRADO Resuelve e inerprea gráficamene las soluciones de las ecuaciones:
Soluciones a los ejercicios propuesos Unidad cuaciones inecuaciones sisemas Maemáicas aplicadas a las Ciencias Sociales CUACIONS D SGUNDO GRADO Resuelve e inerprea gráficamene las soluciones de las ecuaciones:
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2008 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva,
CAPITULO 2: Movimiento en una dirección [S.Z.F.Y. 2]
![CAPITULO 2: Movimiento en una dirección [S.Z.F.Y. 2] CAPITULO 2: Movimiento en una dirección [S.Z.F.Y. 2]](/thumbs/87/96684426.jpg) UNIVERSIDAD TECNOLÓGICA NACIONAL Faculad Regional Rosario UDB Física Cáedra FÍSICA I CAPITULO : Movimieno en una dirección [S.Z.F.Y. ] Cinemáica: La Cinemáica se ocupa de describir los movimienos de los
UNIVERSIDAD TECNOLÓGICA NACIONAL Faculad Regional Rosario UDB Física Cáedra FÍSICA I CAPITULO : Movimieno en una dirección [S.Z.F.Y. ] Cinemáica: La Cinemáica se ocupa de describir los movimienos de los
SEGUNDO EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
By C 10. SEGMENTARIA GEOMETRÍA-ECUACIÓN DE LA RECTA Y POSICIONES. Esta forma se obtiene a partir de la forma general. Ejemplo:
 GEOMETRÍA-ECUACIÓN DE LA RECTA Y POSICIONES Prof: F. Lópe- D. Legal: M-0006/009 0. SEGMENTARIA Esa forma se obiene a parir de la forma general. 0 B C Y A C C B C A C B A C B A Ejemplo: 0 Los denominadores
GEOMETRÍA-ECUACIÓN DE LA RECTA Y POSICIONES Prof: F. Lópe- D. Legal: M-0006/009 0. SEGMENTARIA Esa forma se obiene a parir de la forma general. 0 B C Y A C C B C A C B A C B A Ejemplo: 0 Los denominadores
ÁLGEBRA (Selectividad 2014) 1 ALGUNOS PROBLEMAS DE ÁLGEBRA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2014
 ÁLGEBR (Selecividad 04) LGUNOS PROBLEMS DE ÁLGEBR PROPUESTOS EN LS PRUEBS DE SELECTIVIDD DE 04 Casilla y León, junio 4 a a+ a+ Sea la mariz = a a+ 3 a+ 4 a a+ 5 a+ 6 a) Discuir su rango en función de los
ÁLGEBR (Selecividad 04) LGUNOS PROBLEMS DE ÁLGEBR PROPUESTOS EN LS PRUEBS DE SELECTIVIDD DE 04 Casilla y León, junio 4 a a+ a+ Sea la mariz = a a+ 3 a+ 4 a a+ 5 a+ 6 a) Discuir su rango en función de los
PROBLEMA 3. a) Determina el valor de a para que la siguiente función sea continua en x = 1:
 EXAMEN COMPLETO Baremo: Se elegirá el o el EJERCICIO B, del que SOLO se harán TRES de los cuaro problemas. LOS TRES PROBLEMAS PUNTÚAN POR IGUAL. Cada esudiane podrá disponer de una calculadora cienífica
EXAMEN COMPLETO Baremo: Se elegirá el o el EJERCICIO B, del que SOLO se harán TRES de los cuaro problemas. LOS TRES PROBLEMAS PUNTÚAN POR IGUAL. Cada esudiane podrá disponer de una calculadora cienífica
SOLUCIONARIO GUÍA ESTÁNDAR ANUAL Energía I: trabajo y potencia mecánica
 SOLUCIONARIO GUÍA ESTÁNDAR ANUAL Energía I: rabajo y poencia mecánica SGUICES020CB32-A16V1 Solucionario guía Energía I: rabajo y poencia mecánica Íem Alernaiva Habilidad 1 D Comprensión 2 C Aplicación
SOLUCIONARIO GUÍA ESTÁNDAR ANUAL Energía I: rabajo y poencia mecánica SGUICES020CB32-A16V1 Solucionario guía Energía I: rabajo y poencia mecánica Íem Alernaiva Habilidad 1 D Comprensión 2 C Aplicación
ÁLGEBRA MANUEL HERVÁS CURSO SOLUCIONES ESPACIO EUCLÍDEO. los escalares 1, 2, 0 respectivamente. Solución x
 ÁLGEBRA MANUEL HERVÁS CURSO - Enunciado Se considera el espacio vecorial SOLUCIONES ESPACIO EUCLÍDEO referido a la base B e, e, e coordenadas en la base dual B* f, f, f. Hallar las de la forma lineal que
ÁLGEBRA MANUEL HERVÁS CURSO - Enunciado Se considera el espacio vecorial SOLUCIONES ESPACIO EUCLÍDEO referido a la base B e, e, e coordenadas en la base dual B* f, f, f. Hallar las de la forma lineal que
Gráficas de curvas trigonométricas
 Capíulo 4 Gráficas de curvas rigonoméricas La definición de las razones rigonoméricas, como funciones del ángulo, lleva implicado el esudio de las funciones rigonoméricas desde el puno de visa de las funciones
Capíulo 4 Gráficas de curvas rigonoméricas La definición de las razones rigonoméricas, como funciones del ángulo, lleva implicado el esudio de las funciones rigonoméricas desde el puno de visa de las funciones
TEMA 2: CINETICA DE LA TRASLACIÓN
 TEMA 2: CINETICA DE LA TRASLACIÓN 1.1. Inroducción. Para ener caracerizado un movimieno mecánico cualquiera, hay que esablecer primero respeco a que cuerpo (s) se va a considerar dicho movimieno. Ese cuerpo
TEMA 2: CINETICA DE LA TRASLACIÓN 1.1. Inroducción. Para ener caracerizado un movimieno mecánico cualquiera, hay que esablecer primero respeco a que cuerpo (s) se va a considerar dicho movimieno. Ese cuerpo
Función es una relación entre dos variables a las que, en general, se les llama x e y. Viene representado por: y f (x)
 TEMA 9: :.- CONCEPTO DE FUNCIÓN: Función es una relación entre dos variables a las que, en general, se les llama e y. Viene representado por: y (, donde es la variable independiente e y es la variable
TEMA 9: :.- CONCEPTO DE FUNCIÓN: Función es una relación entre dos variables a las que, en general, se les llama e y. Viene representado por: y (, donde es la variable independiente e y es la variable
IES Fco Ayala de Granada Suplente Junio de 2017 (Modelo 4) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Suplene Junio de 07 (Modelo 4) Germán-Jesús Rubio Luna Opción A Ejercicio opción A, Suplene Junio 07 (modelo 4) x+ si x < 0 Se sabe que la función f : R R dada por f(x) = x + acos(x)
IES Fco Ayala de Granada Suplene Junio de 07 (Modelo 4) Germán-Jesús Rubio Luna Opción A Ejercicio opción A, Suplene Junio 07 (modelo 4) x+ si x < 0 Se sabe que la función f : R R dada por f(x) = x + acos(x)
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 .E.S. CSTELR DJOZ. Menguiano PRUE DE CCESO (LOGSE) UNVERSDD DE LERES SEPTEMRE - (RESUELTOS por ntonio Menguiano) MTEMÁTCS Tiepo áio: horas inutos Contesta de anera clara raonada una de las dos opciones
.E.S. CSTELR DJOZ. Menguiano PRUE DE CCESO (LOGSE) UNVERSDD DE LERES SEPTEMRE - (RESUELTOS por ntonio Menguiano) MTEMÁTCS Tiepo áio: horas inutos Contesta de anera clara raonada una de las dos opciones
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2001 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
MOVIMIENTO RECTILÍNEO
 Transparencia Nº 1. CINEMÁTICA. MOVIMIENTO QUÉ ES EL MOVIMIENTO? Cambio de posición de un móvil con el iempo. TIPOS DE MOVIMIENTO Según su rayecoria Todo movimieno es RELATIVO Lo rápido del cambio lo indoca
Transparencia Nº 1. CINEMÁTICA. MOVIMIENTO QUÉ ES EL MOVIMIENTO? Cambio de posición de un móvil con el iempo. TIPOS DE MOVIMIENTO Según su rayecoria Todo movimieno es RELATIVO Lo rápido del cambio lo indoca
Calcular el área del paralelogramo si las diagonales son los vectores 2U V
 x + y z 3 1. Hallar la disancia d de la reca L: = = al plano π que coniene al riángulo de vérices A(, 1, 4), 1 1 4 (1,, -8) y C(, -3, 4) Ax + y + Cz + D Aplicando la disancia de un puno a un plano: d =
x + y z 3 1. Hallar la disancia d de la reca L: = = al plano π que coniene al riángulo de vérices A(, 1, 4), 1 1 4 (1,, -8) y C(, -3, 4) Ax + y + Cz + D Aplicando la disancia de un puno a un plano: d =
Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica Guía para el ETS de Cálculo Vectorial IE ICA ISISA
 Funciones Vecoriales Insiuo Poliécnico Nacional 1. Para cada función vecorial, calcule r' ( r ''( 1.1 r( (sin cos i cos j sink (Res r' ( cosi sin j cosk 1. r( (cos i e j (1/ k (Res. r'( sin i e j (1/ k.
Funciones Vecoriales Insiuo Poliécnico Nacional 1. Para cada función vecorial, calcule r' ( r ''( 1.1 r( (sin cos i cos j sink (Res r' ( cosi sin j cosk 1. r( (cos i e j (1/ k (Res. r'( sin i e j (1/ k.
Solución 3.- OPERACIONES CON MATRICES y 1 1 0
 .- CONCEPTO DE MATRIZ 3 7 Escriba la mariz 2 x 3 en la que a ij = 5i 4j Solución : 6 2 2 2 Calcule, si es posible, los valores de a y b para que sean iguales las marices 3a b 9 b a 7 2b a 7 A= B= a+ b
.- CONCEPTO DE MATRIZ 3 7 Escriba la mariz 2 x 3 en la que a ij = 5i 4j Solución : 6 2 2 2 Calcule, si es posible, los valores de a y b para que sean iguales las marices 3a b 9 b a 7 2b a 7 A= B= a+ b
XA + A B = A, siendo 0 0 1
 MATEMÁTICAS II PROBLEMAS DE ÁLGEBRA PAU ANDALUCÍA Ejercicio. (Examen Junio 202 Específico Opción A) 2 0 [2'5 punos] Considera las marices AA = 0 2, BB = 0 2 0 y CC = 0 2. 2 Deermina, si exise, la mariz
MATEMÁTICAS II PROBLEMAS DE ÁLGEBRA PAU ANDALUCÍA Ejercicio. (Examen Junio 202 Específico Opción A) 2 0 [2'5 punos] Considera las marices AA = 0 2, BB = 0 2 0 y CC = 0 2. 2 Deermina, si exise, la mariz
PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE Apellidos Nombre. DNI / NIE Centro de examen
 CALIFICACIÓN: Consejería de Educación, Ciencia y Culura PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE 011 Resolución de 9 de marzo de 011 (DOCM de 5 de abril)
CALIFICACIÓN: Consejería de Educación, Ciencia y Culura PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE 011 Resolución de 9 de marzo de 011 (DOCM de 5 de abril)
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 OPCIÓN A 0 1 0 0 1 1 Sean las marices C = 1 0 1 y D = 1 0 1. 0 1 0 1 1 0 a) (1.5 punos) Resuelva la ecuación maricial 2 X C D = ( I 3 + D) C. b) (1 puno) Si las marices C y D son las marices de adyacencia
OPCIÓN A 0 1 0 0 1 1 Sean las marices C = 1 0 1 y D = 1 0 1. 0 1 0 1 1 0 a) (1.5 punos) Resuelva la ecuación maricial 2 X C D = ( I 3 + D) C. b) (1 puno) Si las marices C y D son las marices de adyacencia
10Soluciones a los ejercicios y problemas PÁGINA 217
 PÁGIN 217 Pág 1 P RCTIC 1 a) Represena en papel cuadriculado la figura H 1 obenida a parir de H mediane la raslación del vecor 1 (3, 2) b) Dibuja la figura H 2 ransformada de H 1 mediane la raslación 2
PÁGIN 217 Pág 1 P RCTIC 1 a) Represena en papel cuadriculado la figura H 1 obenida a parir de H mediane la raslación del vecor 1 (3, 2) b) Dibuja la figura H 2 ransformada de H 1 mediane la raslación 2
