INTRODUCCIÓN. Cada tema se divide en tres partes: Teoría Problemas resueltos Problemas propuestos
|
|
|
- Sofia Quintana Muñoz
- hace 8 años
- Vistas:
Transcripción
1
2 INTRODUCCIÓN Al trbjr en el ul con lumnos sordos nos dmos cuent de que su grn problem es l dificultd que estos lumnos tienen en l comunicción tnto orl como escrit. L que l myorí de ls persons sords considern su lengu nturl, l Lengu de Signos, es un lengu con un estructur distint l de l lengu cstelln, y el signo o los signos usdos por ests persons pr denotr un objeto o un concepto son distintos l sucesión de símbolos que se emplen en l lengu escrit pr denotr dicho objeto o concepto. Por est rzón, pr estos lumnos, el enfrentrse culquier libro de texto implic un doble dificultd: l dificultd propi de l mteri trtd por el libro y l dificultd de l lengu en l que están escritos dichos libros. En este libro presentmos cinco tems dptdos este tipo de lumndo con l doble intención de hcerles llegr de un mner sencill estos cinco tems y de umentr su comprensión lector. L dptción que relizmos no consiste en eliminr de su curriculum prtes de un tem o conceptos complicdos sino que es un dptción metodológic en l que intentmos enseñr lo mismo pero usndo un serie de recursos más visules y más cercnos su lengu. Los tems desrrolldos en este libro son: Los números nturles. Los números enteros. Los números rcionles. Los números irrcionles. Los números reles. que no se corresponden con el curricilum de ningún curso pero que sí formn un bloque importnte que se estudi desde los primeros cursos de primri hst primero de bchillerto. Así, el primer tem es borddo por lumnos oyentes en l etp de primri, pero pr un person sord l resolución de problems con texto result muy complicd y se pospone su estudio hst l etp de secundri. Los tems y se estudin de form cíclic lo lrgo de tod l secundri. Los tems y se desrrolln sobre todo en º de E. S. O. en Mtemátics opción B y en º de Bchillerto. Cd tem se divide en tres prtes: Teorí Problems resueltos Problems propuestos El prtdo de teorí se reliz siempre doble págin: Texto dptdo Texto norml
3 En ls págins derechs se encuentr l teorí correspondiente l tem trtdo en lengu cstelln, tl y como prece en culquier libro de mtemátics. En ls págins izquierds se dpt el texto de l págin derech utilizndo distintos recursos: frses corts y dptds un estructur más cercn l de l Lengu de Signos, dibujos, esquems, color,... Además en ests págins izquierds se us el mrgen pr clrr expresiones o plbrs del texto que los lumnos sordos nos hn indicdo que no conocen. En este cso l plbr o expresión no conocid se pone en cursiv en el texto, y se clr l mrgen con un dibujo ilustrtivo o un signo o un sinónimo,... Además se us tmbién el mrgen pr recordrles conceptos y pr indicrles cómo se leen determinds expresiones mtemátics o cómo se leen lgunos números, como por ejemplo lguns frcciones, ríces,... El motivo por el que se escribió l teorí doble págin er pr que los lumnos fuesen cpces de entenderl en ls págins izquierds y pudiern comprr con ls págins derechs y de est form, en un futuro, sen cpces de entender otros libros de mtemátics. El formto de los dos prtdos siguientes, problems resueltos y problems propuestos, es diferente l de l teorí y que en mbos prtdos no hy distinción entre págins derechs e izquierds. En mbos csos los enuncidos precen tl y como pueden precer en culquier exmen o libro de texto, y sólo llevn clrdo l mrgen, con un signo, un dibujo, un explicción o usndo sinónimos, tods quells plbrs o expresiones que los lumnos sordos de nuestro centro nos hn indicdo que desconocen, en este cso dichs plbrs o expresiones precen en cursiv en el texto. Ls soluciones los problems resueltos tienen un estructur diferente l que podemos encontrr en otros libros. Aquí sustituimos explicciones lrgs y con mucho vocbulrio por esquems, dibujos, color y frses corts con un estructur dptd pr que resulte más cercn l estructur de l Lengu de Signos, unque intentndo que est estructur se correct en Lengu Cstelln. En el cso de los problems propuestos sólo prece l solución finl. Al usr estos libros el lumno se costumbr intentr entender el texto, solicitndo pr quells plbrs o expresiones que él desconoce y que no están clrds l mrgen lgun explicción que él mismo ñdirá. Normlmente, trs l explicción del profesor, el lumno entiende por sí solo los problems resueltos que le sirven de put pr relizr los problems propuestos. Tmbién usrá estos libros como mteril de consult en cursos posteriores pr recordr conceptos olviddos, pues su mnejo les result no demsido complicdo. Mª Trinidd Cámr Meseguer Coordindor del proyecto I.E.S. Jun Crlos I Murci
4 TEMA I: LOS NÚMEROS NATURALES Autors: Mª José Fernández Hurtdo Mª Belén Rmírez Hellín
5 TEXTO ADAPTADO LOS NÚMEROS NATURALES Nosotros podemos usr muchos números, el conjunto más pequeño de esos números es el conjunto de los números nturles. Su signo es l letr N y los números nturles son 0,,,... N {0,,,,...} Estos números se empezron usr hce mucho tiempo, y se usn mucho pr contr coss, unque nosotros tmbién ls usmos pr otrs coss: contr Ejemplo: Cuántos ños tienes? Cuántos hermnos sois? Cuánto tiempo dur l clse de mtemátics? 0 minutos En l histori hy muchs forms de escribir los números nturles, nosotros hor usmos un form que se llm sistem de numerción deciml. En este sistem usmos diez símbolos: 0,,,,,,, 7, 8, 9. Un símbolo quiere decir un cntidd u otr cntidd, depende el lugr dónde esté. En los siguientes ejemplos el número está en distintos lugres y en cd lugr signific un cntidd distint. se dice cinco 0 se dice cincuent 00 se dice quinientos Número Quiere decir cntidd uniddes ( ) 0 decens (cinco veces ) 00 centens (cinco veces ) 9 se dice nueve se dice cutro Recuerd que:. Un número de un cifr tiene uniddes. Por ejemplo 9 9 uniddes uniddes. Un número de dos cifrs tiene decens y uniddes. decens uniddes se dice treint y uno Por ejemplo decens uniddes decens y unidd veces diez y unidd 0 + se dice quinientos curent y tres. Un número de tres cifrs tiene centens, decens y uniddes. centens decens uniddes Por ejemplo centens decens uniddes centens, decens y uniddes veces cien, veces diez y uniddes
6 LOS NÚMEROS NATURALES Los números nturles son el conjunto más pequeño de números que podemos usr, se representn por N y son 0,,,,,... N {0,,,,,...} Estos números se comenzron utilizr hce mucho tiempo y sirven sobre todo pr contr objetos unque nosotros los utilizmos en numeross plicciones. Cuántos ños tienes? Cuántos hermnos sois? Cuánto dur l clse de mtemátics? 0 minutos A lo lrgo de l histori hn existido muchs forms de escribir los números nturles, l que nosotros usmos ctulmente se llm sistem de numerción deciml. En este sistem utilizmos diez símbolos: 0,,,,,,, 7, 8, y 9. Dependiendo de l posición que ocupen estos símbolos significrán un u otr cntidd. Así, en los siguientes csos el número ocup distints posiciones y signific distints cntiddes: Número Cntidd que represent uniddes 0 decens, es decir, cinco veces diez 00 centens, es decir, cinco veces cien Recuerd que:. Un número de un cifr está formdo por uniddes. Por ejemplo 9 9 uniddes uniddes. Un número de dos cifrs está formdo por decens y uniddes. decens uniddes Por ejemplo decens uniddes decens y unidd veces diez y unidd 0 +. Un número de tres cifrs está formdo por centens, decens y uniddes. centens decens uniddes Por ejemplo centens decens uniddes centens, decens y uniddes veces cien, veces diez y uniddes
7 TEXTO ADAPTADO. Si hy más cifrs se hce igul, por ejemplo, un número de cifrs tiene decens de millr, uniddes de millr, centens, decens y uniddes..0 se dice cincuent y cutro mil trescientos uno. decens de millr uniddes de millr centens decens uniddes Por ejemplo.0 decens de millr uniddes de millr centens decens uniddes 0 decens de millr, uniddes de millr, centens, 0 decens y unidd veces diez mil, veces mil, veces cien, 0 veces diez y unidd REPRESENTACIÓN DE NÚMEROS NATURALES Los números nturles se pueden representr (dibujr) en un rect. Primero dibujmos en l rect un punto, que vle 0 y cogemos un medid (por ejemplo cm.) pr hcer los psos. Pr dibujr culquier número, por ejemplo el, cogemos el 0 y dmos psos l derech, igul que el dibujo: 0 el 8: 0 8 Si por ejemplo el número es muy grnde cogemos un unidd más pequeñ (pso más corto). Por ejemplo pr dibujr el número : 0 ORDENACIÓN DE NÚMEROS NATURALES Notción mtemátic: < quiere decir menor > quiere decir myor quiere decir igul igul quiere decir menor o quiere decir myor o igul < 7 < se dice dos menor que siete menor que once Pr ordenr números nturles hy dos forms:. Dibujmos todos los números en un rect como hemos explicdo ntes. Ahor leemos los números desde l izquierd hst l derech ( ) y y están ordendos de menor (más pequeño) myor (más grnde). Por ejemplo pr ordenr los números 7, y primero los dibujmos: 0 7 Ahor leemos de izquierd derech: después 7 después entonces < 7 < Est form vle cundo los números son pequeños.
8 . Así con culquier cntidd de cifrs, por ejemplo, si tiene cifrs está formdo por decens de millr, uniddes de millr, centens, decens y uniddes. decens de millr uniddes de millr centens decens uniddes Por ejemplo 0 decens de millr uniddes de millr centens decens uniddes 0 decens de millr, uniddes de millr, centens, 0 decens y unidd veces diez mil, veces mil, veces cien, 0 veces diez y unidd REPRESENTACIÓN DE NÚMEROS NATURALES Podemos representr los números nturles sobre un rect. Pr ello, tomremos en est rect un punto como el vlor 0 y un medid como longitud, por ejemplo un centímetro. A prtir de hí pr dibujr culquier vlor, por ejemplo el, mediremos l derech del 0 tres uniddes de longitud como muestr l figur: 0 el 8: 0 8 Si el número es muy grnde cogeremos un unidd de medid menor. Por ejemplo pr representr el número podrímos: 0 ORDENACIÓN DE NÚMEROS NATURALES Pr ordenr números nturles podemos hcerlo de dos forms: Cso I: Dibujmos los números sobre un rect como hemos explicdo en el cso nterior. Si leemos los números dibujdos de izquierd derech estremos ordenndo los números de menor myor. Por ejemplo pr ordenr los números 7, y los dibujmos sobre l rect: 0 7 Y hor leemos de izquierd derech: después 7 después luego < 7 < Notción mtemátic: < signific menor > signific myor signific igul signific menor o igul signific myor o igul Este método se us si los números son pequeños.
9 TEXTO ADAPTADO. Si por ejemplo los números son grndes, hcer el dibujo es difícil, entonces podemos ordenrlos con yud de uns norms: se dice dos 0 se dice ciento diez se dice once 78 se dice cutro mil trescientos setent y ocho. Si un número tiene menos cifrs y otro número tiene más cifrs, el número con menos cifrs es el número más pequeño. Ejemplo: Ordenr, 0, y 78, 0,, 7 8 () () () () cifrs El número más pequeño es el ( cifr) después el ( cifrs) después el 0 ( cifrs) y último el 78 ( cifrs) < < 0 < 78 7 se dice trescientos veintisiete se dice trescientos cincuent y uno se dice quinientos treint y cinco se dice quinientos treint y uno 7 se dice veintisiete se dice curent y uno se dice doscientos treint y uno 7 se dice doscientos treint y siete. Si los números tienen ls misms cifrs, por ejemplo cifrs los dos, primero mirmos ls centens, si ls centens son igules mirmos ls decens. Si ls decens son igules mirmos ls uniddes. Ejemplos: Ordenr los números 7 y. 7 centens igules decens < entonces 7 < Ordenr los números y. centens igules uniddes < entonces < decens igules Ordenr los números 7,,, y 7. Hy números de dos cifrs: 7, y y otros números con tres cifrs: y 7. Primero ordenmos los números de dos cifrs: 7 < < entonces < 7 < Segundo ordenmos los de cifrs: 7 centens igules uniddes < 7 entonces < 7 decens igules Los números de dos cifrs son más pequeños, entonces el orden es: < 7 < < < 7
10 Cso II: Si los números son grndes hcer el dibujo es complicdo, en este cso, podemos ordenrlos siguiendo ls siguientes norms:. Si dos número tienen distints cifrs, el número menor es el que menos cifrs tiene. Ejemplo: Ordenr, 0, y 78 cifr (el ) 0 cifrs (el, el y el 0) cifrs (el y el ) 78 cifrs (el, el, el 7 y el 8) Entonces el es el más pequeño ( cifr) después el ( cifrs) después el 0 ( cifrs) y después el 78 ( cifrs) < < 0 < 78. Si tienen ls misms cifrs, por ejemplo cifrs, comprmos primero ls centens, si son igules, comprmos ls decens, si son igules, comprmos ls uniddes. Ejemplos: Ordenr los números 7 y. 7 centens igules decens < entonces 7 < Ordenr los números y. centens igules uniddes < entonces < decens igules Ordenr los números 7,,, y 7. Aquí hy números de dos cifrs: 7, y y números de tres cifrs: y 7. Ordenmos primero los números de dos cifrs: 7 < < entonces < 7 < ordenmos hor los números de tres cifrs: 7 centens igules uniddes < 7 entonces < 7 decens igules Como los números de dos cifrs son menores que los de tres cifrs, entonces el orden es: < 7 < < < 7 7
11 TEXTO ADAPTADO OPERACIONES CON NÚMEROS NATURALES UNIR SUMAR Recuerd que pr solucionr problem debes seguir los siguientes psos:. Leer despcio.. Ver qué dice el problem dtos del problem.. El problem... qué pregunt?... qué me pide?. Qué operción (sum, rest,...) debo utilizr? JUNTAR SUMAR Con los números nturles podemos hcer lguns operciones (cálculos): Sum Cundo en un problem (ejercicio) tú quieres UNIR vrios conjuntos de coss, utiliz l SUMA. Ejemplos:. En º A hy lumnos, en º B hy 9 lumnos y en º C hy 7 lumnos. En totl, cuántos lumnos hy?. Ayer me compré vris coss: un vestido que vlí, unos pntlones por 0 y un jersey de. En totl, yo gsté... cuánto? Pr solucionr estos problems, hcemos los psos que hy en el mrgen. Ejemplo :. leer despcio: En º A hy lumnos, en º B hy 9 lumnos y en º C hy 7 lumnos. En totl, cuántos lumnos hy?. Dtos del problem: º A lumnos º B 9 lumnos º C 7 lumnos. El Problem... qué pregunt?... qué me pide? En totl, cuántos lumnos hy?. Qué operción debo utilizr? sum?, rest?, multiplicción?,... Yo quiero UNIR los lumnos de º A, º B y º C quiere decir que debo SUMAR, 9 y lumnos hy en totl. Ejemplo :. leer despcio: Ayer me compré vris coss: un vestido que vlí, unos pntlones por 0 y un jersey de. En totl, yo gsté... cuánto?. Dtos: Vestido Pntlón 0 Jersey. El Problem... qué pregunt?... qué me pide? Yo gsté... Cuánto dinero?. sum?, rest?, multiplicción?,... Pr sber cuánto dinero he gstdo en el vestido, el pntlón y el jersey JUNTOS tengo que SUMAR el precio del vestido más el precio del pntlón más el jersey Los números dentro de l sum tienen un nombre especil, se llmn sumndos y el resultdo se llm sum. Ejemplo: 0 sumndos + 8 sum 8
12 OPERACIONES CON NÚMEROS NATURALES Con los números nturles podemos relizr ls siguientes operciones: Sum Se sumn números en quellos problems en los que queremos UNIR vrios conjuntos de coss. Ejemplos:. En l clse de º A hy lumnos, en º B hy 9 lumnos y en º C hy 7 lumnos. Cuántos lumnos hy en los tres cursos?. Ayer compré un vestido que me costó, unos pntlones que me costron 0 y un jersey que me costó Cuánto dinero me gsté? Pr resolver estos ejemplos seguiremos los psos indicdos en el mrgen. Así en el ejemplo tenemos:. leer despcio: En l clse de º A hy lumnos, en º B hy 9 lumnos y en º C hy 7 lumnos. Cuántos lumnos hy en los tres cursos?. Dtos del problem: Alumnos de º A Alumnos de º B 9 Alumnos de º C 7. Qué me pide el problem? Cuántos lumnos hy en los tres cursos?. Qué operción debo hcer? Debo UNIR los lumnos de º A, º B y º C, es decir, debo SUMAR, 9 y lumnos hy en los tres cursos. Vmos resolver hor el ejemplo :. leer despcio: Ayer compré un vestido que me costó, unos pntlones que me costron 0 y un jersey que me costó Cuánto dinero me gsté?. Dtos del problem: Precio del vestido Precio del pntlón 0 Precio del jersey. Qué me pide el problem? Cuánto dinero me gsté?. Qué operción debo hcer? Quiero sber lo que me hn costdo el vestido, el pntlón y el jersey JUNTOS, es decir, SUMAR el precio del vestido, el pntlón y el jersey UNIR SUMAR Recuerd que pr resolver culquier problem debes seguir los siguientes psos:. Leerlo despcio.. Ver qué informción nos dn dtos del problem.. Ver qué me pide el problem.. Qué operción (sum, rest,...) debo hcer? JUNTAR SUMAR Los números que intervienen en un sum tienen un nombre especil, se llmn sumndos y el resultdo se llm sum. Ejemplo: 0 sumndos + 8 sum 9
13 TEXTO ADAPTADO DIFERENCIA RESTAR En l sum el orden (de los sumndos) NO import: d igul 8 Rest: Se restn números pr qué? Pr sber l DIFERENCIA entre esos dos números. Ejemplos:. En el instituto de Molin hy 700 lumnos y en el instituto Jun Crlos I hy.7 lumnos. ) Dónde hy más lumnos? b) Qué diferenci de lumnos hy entre los dos institutos?. Es mi cumpleños y he comprdo un trt que vle 9. Yo tení, cuánto dinero sobr? Ejemplo. Leemos despcio y vemos: Dtos: Instituto Molin 700 lumnos Instituto Jun Crlos I.7 lumnos qué preguntn? Me preguntn dos coss ) y b): ) Dónde hy más lumnos? Tengo que mirr los números y mirr cuál es más grnde 7 0 0, 7 () () SOBRA RESTAR cifrs Entonces.7 es más grnde (porque tiene más cifrs) y entonces el instituto Jun Crlos I tiene más lumnos. b) Qué diferenci de lumnos hy entre los dos institutos? Tú sbes que DIFERENCIA RESTA, Entonces tengo que restr los lumnos de los dos institutos: lumnos hy de diferenci. Ejemplo : Dtos: L trt vle 9 Yo tengo Nos preguntn: cuánto dinero sobr? SOBRA RESTA Dinero que tení dinero que gsto dinero que sobr 9 sobrn. En l rest los números tmbién tienen un nombre especil: 7 minuendo 7-0 sustrendo - 78 rest 89 Cundo termines l rest puedes comprobr si está bien, cómo? con un fórmul: rest + sustrendo minuendo Ejemplo: l rest está bien l rest está bien. En l rest el orden de los números es muy importnte, NO se puede cmbir. 0
14 En un sum no import el orden de los sumndos: 7 cmbimos el orden de los sumndos d el mismo resultdo 8 Rest: Se restn dos números cundo queremos sber l DIFERENCIA entre esos dos números. Ejemplos:. En el instituto de Molin hy 700 lumnos y en el instituto Jun Crlos I hy.7 lumnos. ) En qué instituto hy más lumnos? b) Cuál es l diferenci de lumnos entre los dos institutos?. He comprdo un trt pr mi cumpleños que me h costdo 9. Si llevb, cuánto dinero me h sobrdo? DIFERENCIA RESTAR Vmos resolver estos ejemplos. Si leemos despcio el ejemplo vemos que los dtos son: Dtos del problem: Instituto de Molin 700 lumnos Instituto Jun Crlos I.7 lumnos Nos piden dos coss: ) En qué instituto hy más lumnos? Es decir, debo comprr dos números (700 y 7) y ver cuál es myor. Como 700 tiene cifrs y.7 tiene cifrs es myor.7, es decir, el instituto Jun Crlos I tiene más lumnos. b) Cuál es l diferenci de lumnos entre los dos institutos? Sbemos que DIFERENCIA RESTAR, luego debo restr el número de lumnos de los dos institutos: lumnos hy de diferenci. En el segundo ejemplo los dtos son: L trt vle 9 Yo tengo Y lo que nos piden es: cuánto dinero me h sobrdo? Pr sber el dinero que me SOBRA necesito hllr l DIFERENCIA entre el dinero que tengo y el que debo de dr por l trt, es decir, RESTAR el dinero que tengo menos el que vle l trt: 9 me sobrn. SOBRA RESTAR Tmbién en l rest los números que intervienen tienen un nombre especil: 7 minuendo 7-0 sustrendo - 78 rest 89 Siempre que hces un rest puedes comprobr si el resultdo está bien o no usndo l siguiente fórmul: rest + sustrendo minuendo Por ejemplo: luego l primer rest está bien luego l segund rest tmbién está bien. En l rest es importnte el orden de los números y NO podemos cmbirlo.
15 TEXTO ADAPTADO Producto Multiplicción Multiplicción: Cundo queremos SUMAR MUCHAS VECES EL MISMO NÚMERO hcemos l multiplicción. Ejemplo: Un lápiz cuest 0 céntimos, lápices cuestn... cuánto? Dtos del problem: lápiz vle 0 céntimos Me preguntn lápices cuestn... cuánto? Yo debo hcer... qué operción? sum?, rest?,... Yo tengo que JUNTAR el dinero del primer lápiz, más el dinero del segundo lápiz, más el precio del tercer lápiz más el precio del curto lápiz. Quiere decir SUMAR SUMAR VARIAS VECES EL MISMO NÚMERO es igul que MUL- TIPLICAR ese número por ls veces. Aquí (veces) 80 céntimos cuestn lápices. En el producto, los números tmbién tienen un nombre especil, se llmn fctores y el resultdo se llm producto. x 8 fctores 0 producto El orden de los fctores d igul: d igul 0 División Cociente División: Se utiliz cundo queremos REPARTIR un cos EN PARTES IGUALES. Ejemplo: Melis tiene crmelos y quiere reprtirlos entre sus tres migs. Entonces, cuántos crmelos drá cd mig? Dtos: Melis tiene crmelos Melis tiene migs Preguntn: Cuántos crmelos d cd mig? Qué hcemos? sum?, rest?,... Quiero REPARTIR los crmelos entre ls migs DIVIDIR : crmelos pr cd mig. Los números de l división tmbién tienen un nombre especil: Dividendo Divisor Resto Cociente Cundo termines l división, tú puedes comprobr si está bien o ml. Se llm l prueb de l división: Divisor x Cociente + Resto Dividendo x + El orden de los números NO se puede cmbir.
16 Multiplicción: Relizremos est operción cundo quermos SUMAR MUCHAS VECES EL MISMO NÚMERO. Ejemplo: Si un lápiz cuest 0 céntimos, cuánto nos costrán lápices? Los dtos de este problem son: lápiz vle 0 céntimos Y nos piden cuánto nos costrán lápices? L operción que debo hcer es: JUNTAR lo que vle el primer lápiz, lo que vle el segundo lápiz, lo que vle el tercer lápiz y lo que vle el curto lápiz, es decir, SUMAR Pero SUMAR VARIAS VECES EL MISMO NÚMERO es igul que MULTIPLICAR el número que sumo por ls veces que lo sumo. Aquí MULTIPLICAR 0 80 céntimos cuestn lápices. En el producto los números que intervienen tmbién tienen un nombre especil, se llmn fctores y el resultdo se llm producto. x 8 fctores 0 producto El orden en que pongmos los fctores d igul: cmbimos el orden de los fctores d el mismo resultdo 0 División: Usremos est operción cundo quermos REPARTIR lgo EN PARTES IGUALES. Ejemplo: Melis tiene crmelos que quiere reprtir entre sus tres migs. Cuántos crmelos drá cd mig? Los dtos del problem son: Melis tiene crmelos Melis tiene migs Qué pide el problem Cuántos crmelos drá cd mig? Qué operción debo hcer? Debo REPARTIR los crmelos entre ls migs, es decir DIVIDIR entre : crmelos pr cd mig. Producto Multiplicción División Cociente Los números que precen en un división tmbién tienen nombre propio: Dividendo Divisor Resto Cociente Siempre que hgs un división puedes comprobr si está bien relizndo l prueb de l división: Divisor x Cociente + Resto Dividendo x + El orden de los números que intervienen en un división no se puede cmbir.
17 TEXTO ADAPTADO JERARQUÍA DE OPERACIONES A veces tienes que hcer un operción (cálculo) con sums, rests, productos y divisiones. Recuerd que hy orden pr hcerlo: º multiplicciones y divisiones por orden de izquierd derech ( ). º sums y rests por orden de izquierd derech ( ). Este orden se puede cmbir con préntesis ( ) o corchetes [ ]. Si hy ( ) o [ ], se hce primero lo que hy dentro. Si hy vrios préntesis o corchetes primero se hce el préntesis o corchete que hy más dentro. Ejemplos:. Clcul + Hy sum y producto primero se hce el producto: + + Ahor hcemos l sum: + 7. Clcul 7 : Hy producto y división. Los dos vlen igul, entonces hcemos por orden. Primero hy producto: 7 : 8 : Ahor hcemos l división: 8 :. Clcul 8 : Hy división y producto. Los dos vlen igul, entonces hcemos por orden. Primero hy división: 8 : Ahor hcemos el producto: 0. Clcul ( + ) Hy préntesis Primero se hce el préntesis siempre:: ( + ) Ahor hcemos el producto:
18 JERARQUÍA DE OPERACIONES Si tienes que relizr un operción en l que precen sums, rests, productos y divisiones recuerd que el orden pr hcerls es el siguiente: º multiplicciones y divisiones en el orden que precen. º sums y rests en el orden que precen. Este orden se puede modificr usndo préntesis y corchetes que tienen l máxim preferenci cundo vys hcer ls operciones. Si hy vrios préntesis o corchetes tendrán preferenci los más internos. Ejemplos:. Clcul + Aquí hy sums y productos, primero debemos hcer el producto: + + Y hor hcemos l sum: + 7. Clcul 7 : Aquí hy productos y divisiones, tienen l mism prioridd, debemos hcer primero lo primero que me encuentro, es decir, el producto: 7 : 8 : Y hor hcemos l división: 8 :. Clcul 8 : Aquí hy divisiones y productos, tienen l mism prioridd, debemos hcer primero lo primero que me encuentro, es decir, l división: 8 : Y hor hcemos el producto: 0. Clcul ( + ) Aquí hy un préntesis que tiene preferenci sobre culquier operción: ( + )
19 PROBLEMAS RESUELTOS
20 . Escribe los siguientes números: ) Mil cutrocientos novent y dos. b) Dos mil uno. c) Seis millones ochent y cinco mil. d) Un millón mil uno. e) Ciento veintisiete mil cutro. ) Unidd de millr centens Decens Uniddes mil cutrocientos novent Dos 9 Mil cutrocientos novent y dos 9 b) Unidd de millr centens Decens Uniddes Dos mil Uno 0 0 Dos mil uno 00 c) d) Unidd de millón Centens de millr Decens de millr Unidd de millr Centens Decens Uniddes Seis Ochent Cinco millones mil Unidd de millón Seis millones ochent y cinco mil Centens de millr Decens de millr Unidd de millr Centens Decens Uniddes Un millón Mil Uno Un millón mil uno e) Centens de millr Decens de millr Unidd de millr Centens Decens Uniddes ciento veinti siete mil cutro Ciento veintisiete mil cutro
21 . Cómo se dicen los siguientes números: ) 0 00 b) 7 08 c) 0 00 ) Centens de millr Decens de millr Unidd de millr Centens Decens Uniddes Ciento Un mil Tres 0 00 ciento un mil tres. b) Decens de millr Unidd de millr Centens Decen s Uniddes Setent Cinco mil Ochent Uno 7 08 setent y cinco mil ochent y uno. c) Unidd de millón Centens de mills Decens de millr Unidd de millr Centens Decens Uniddes Dos millones Cutrocien tos Seis mil Cutrocien tos Represent dibuj 0 00 dos millones cutrocientos seis mil cutrocientos.. Represent sobre un rect los números:,, 9, y ordénlos de menor myor. Dibujmos un rect y ponemos un punto 0 0 y ponemos el número (donde tú quiers) 0 Ahor psos l derech cuántos? número mnd:,, 9 y 0 9 Orden números cuál? después después después 9 < < < 9 8
22 . Orden los siguientes números: 7, 7, 8,,, 7. º Cuánts cifrs tiene cd número? 7 cifrs (el y el 7) 7 cifrs (el, el 7 y el ) 8 cifrs (el, el y el 8) cifrs (el, el y el ) cifrs (el y el ) 7 cifrs (el, el y el ) Entonces: más pequeños números con cifrs: 7 y después números con tres cifrs:, 8,, 7 Ahor vmos ordenr los números de cifrs: 7 y. 7 7 cifrs cifrs decens igules uniddes < 7 entonces < 7 Después ordenmos los números de cifrs:, 8,, 7. Mirmos ls centens: 8 7 < entonces 8 y 7 son más pequeños, 7 y son más grndes Vmos ordenr 8 y 7 mirndo ls decens: 8 7 centens igules uniddes 7 < 8 entonces 7 < 8 decens igules Ahor ordenmos 7 y : Mirmos ls decens: 7 centens igules decens < 7 entonces < 7 Si juntmos todo tenemos: < 7 < 7 < 8 < < 7. Reliz ls siguientes operciones: ) e) b) 07 f) c) 09 : g) 78 : 7 d) h) ) b) c) 09 : 9 resto 0 d) e) f) g) 78 : 7 0 resto 7 h)
23 . En mi instituto hy dos intérpretes de lengu de signos. Pepi tiene ños y Belén cutro ños más, cuántos ños tiene Belén? Pepi ños Belén ños más Belén ños? Dtos Pregunt Operción JUNTAR ños de Pepi y ños más SUMAR ños de Pepi y más + 7 ños tiene Belén. 7º se dice siete grdos 7. Si el termómetro ls 9 de l mñn en l Plz de Rome mrcb 7º y ls hors hbí umentdo º C. Cuál será l tempertur es hor? Qué quieren decir hors? Debes prender que hy dos forms de reloj. RELOJ ANALÓGICO termómetro umentdo más RELOJ DIGITAL El reloj nlógico mrc l, ls,... hst ls y después por l trde otr vez l, ls,... hst ls. El reloj digitl mrc desde ls 0 hors hst ls. Desde ls 0 hst ls igul que el reloj nlógico. Si son números myores que (,,...), entonces restmos y es l hor por l trde. Y sbemos los relojes, hor empezmos el problem. Dtos A ls 9 hors 7º A ls hors ( - de l trde) ument º. Pregunt A ls hors de l trde tempertur? Operción A ls hors l tempertur AUMENTA AUMENTAR quiere decir que l tempertur es MAYOR (MÁS clor) MÁS SUMAR Entonces l tempertur ls de l trde tempertur ls 9 de l mñn + AUMENTO 7 + 9º C 0
24 8. Ayer fuimos de Murci Archen que están seprds Km. Después de comer llí subimos hst Ricote recorriendo Km. más, desde llí regresmos Murci por el mismo cmino. Cuántos kilómetros recorrimos en totl? Archen Km seprds distnci entre dos lugres regresmos volver recorrimos en totl ir y venir Km volver Ricote Murci Murci hst Archen Km. Archen hst Ricote Km. Ir y venir Km.? Dtos Pregunt Operción JUNTAR Km. pr ir y Km. pr venir SUMAR Km. pr ir y Km. pr venir. Km. pr ir JUNTAR Km. desde Murci hst Archen y Km. desde Archen hst Ricote SUMAR Km. desde Murci hst Archen + Km. desde Archen hst Ricote + 7 Km. pr venir Km. pr ir (l mism crreter) 7 Km en totl JUNTAR Km. pr ir y Km. pr venir Km 9. Esmerld llev hors de pseo con sus migs. Si slieron ls de l trde, qué hor es? Dtos Esmerld hors de pseo Esmerld slió ls de l trde Pregunt Ahor hor? Operción Esmerld sle ls de l trde hor psendo 7 de l hor psendo 8 de l trde trde... SUMAR hor de slid y hors psendo + 0 hors.
25 0. Mi crter llen de libros pes 00 grmos. Si los libros pesn 000 grmos, cuánto pes l crter? Dtos L Crter y los libros pesn.00 gr. Los libros pesn.000 gr. Pregunt L crter pes gr.? Operción El peso de l crter DIFERENCIA entre el peso de l crter y los libros (juntos) menos el peso de los libros RESTAR el peso de l crter y los libros (juntos) menos el peso de los libros grmos pes l crter. lrededor. Cundo l Tierr h ddo 00 vuelts lrededor del Sol. Cuánts le fltn pr dr 000 vuelts? FALTAR RESTAR Debe dr.000 vuelts H ddo y.00 vuelts fltn vuelts? Dtos Pregunt Operción Vuelts que FALTAN DIFERENCIA entre ls vuelts que tiene que hcer y ls vuelts que y h hecho RESTAR ls vuelts que tiene que hcer y ls vuelts que y h hecho vuelts fltn. Este ño en mi clse, empezremos el curso veinticinco lumnos. Si sólo hy nueve chicos, cuánts chics hy? Dtos lumnos (chicos y chics juntos) chicos 9 Pregunt chics cuánts?
26 Operción chics DIFERENCIA entre todos los lumnos (chics y chicos juntos) menos ls chics RESTAR todos los lumnos (chics y chicos juntos) menos ls chics - 9 chics. Quiero comprr un libro que cuest y sólo llevo 8. Cuántos euros me fltn? Recuerd: Normlmente: El libro vle yo tengo 8 Fltn? Dtos Pregunt Operción FALTAR RESTAR Yo necesito Yo tengo 8 8 < entonces FALTAN Los que FALTAN DIFERENCIA entre lo que necesito menos lo que tengo 8 me fltn. Pr comprr un reglo que cuest tenemos 8, cuántos euros sobrn? SOBRAR RESTAR El reglo vle Tenemos 8 Sobrn? Dtos Pregunt Operción Necesitmos Tenemos 8 8 > entonces SOBRAN Los que SOBRAN DIFERENCIA entre lo que tenemos y lo que necesitmos 8 me sobrn. Hll el doble de: ) 0 b) c) 7 Debes prender que DOBLE ) 0 0 b) 70 c) 7
27 . Hll el triple de: ) b) 7 c) 8 Debes prender que TRIPLE ) 9 b) 7 8 c) 8 7. Hll l mitd de: ) 8 b) 8 c) Debes prender que MITAD : : ) 8 : b) 8 : c) 8 8. El sábdo psdo un grupo de migos fuimos cenr y después l cine. En l cen estuvimos seis migos pero l cine fuimos el doble. Cuántos migos fuimos l cine? A cenr vn migos Al cine vn el doble Al cine, cuántos migos vn? Dtos Pregunt Operción Al cine vn el DOBLE migos vn l cine. 9. Cuántos minutos tienen tres hors? Dtos No hy pero sbemos que hor 0 minutos Pregunt hors minutos? Operción Sbemos que hor0 minutos. Pr sber los minutos de hors JUNTAMOS los minutos de l ª hor, l ª hor y l ª horsumar VECES 0MULTIPLICAR por minutos tienen hors.
28 0. Se clcul que por término medio visitn l torre Eiffel cd dí de Semn Snt 000 persons. Cuánts persons visitron l torre Eiffel en dich semn? Dtos dí de Semn Snt visitn l torre Eiffel 000 persons Pregunt En Semn Snt vn l torre Eiffel persons? Operción JUNTAR ls persons que vn l torre Eiffel el lunes, el mrtes, el miércoles,... SUMAR 7 VECES.000 MULTIPLICAR 7 por persons visitron l torre Eiffel en Semn Snt.. Mrí coleccion sellos. En un álbum de 0 págins, cuántos sellos podemos poner si en cd págin cben sellos? torre Eiffel torre fmos en Prís Álbum 0 págins págin sellos En todo el álbum sellos? Dtos Pregunt Operción álbum de sellos álbum dentro pones sellos JUNTAR sellos de l ª págin, de l ª págin, de l ª págin,... SUMAR 0 (0 págins) VECES MULTIPLICAR 0 por 0 0 sellos.. Quiero un equipo de músic que cuest 0 y lo quiero pgr en 0 meses. Cuántos euros debo pgr cd mes? Equipo de músic vle 0 Pgo en 0 meses mes? Dtos Pregunt Operción equipo de músic REPARTIR lo que vle entre los meses DIVIDIR 0 entre No sobr nd Pg cd mes
29 . Tengo 0 y quiero comprr vrios C. D. de músic. Si cd C. D. cuest 8 Cuántos C. D. puedo comprr? Cuántos euros me sobrn? Tengo 0 C. D. vle 8 Compr C. D. cuántos? Sobr cuánto? Dtos Pregunt Operción Debo REPARTIR 0 en grupos de 8 (cd grupo compro C. D.) DIVIDIR 0 entre colocr poner estnterís Sobrn Puedo comprr C. D. Recuerd: el resto de l división lo que sobr de reprtir en prtes igules.. Este curso me he comprdo ctorce libros. De otros ños tení gurddos libros. Si quiero colocr estos libros en un estnterí y sé que en cd lej puedo poner once libros, cuánts lejs necesitré pr colocr todos estos libros? Dtos Este ño libros. Otros ños libros lej cben libros Pregunt JUNTAMOS los libros y los ponemos en lejs. Cuánts lejs necesito? lej Operción º JUNTAR libros SUMAR libros de este ño + libros de otros ños + 7 libros tengo º REPARTIR los 7 libros en lejs DIVIDIR los 7 libros en grupos de libros ( libros en lej) 7 Sobrn libros Necesito lejs complets TOTAL: lejs: dónde los ponemos? Otr lej lejs complets lej con libros
30 . A un excursión orgnizd por el instituto vn 7 lumnos y profesores. Si en cd utobús cben 0 persons. Cuántos utobuses hy que contrtr? Cuánts plzs sobrn? Dtos A l excursión vn 7 lumnos profesores utobús 0 plzs Pregunt Cuántos utobuses? Cuánts plzs sobrn? Operción º JUNTAR lumnos y profesores (pr sber persons en totl) SUMAR 7 y persons vn de excursión. º REPARTIR 9 persons en grupos de 0 (persons en el mismo utobús) DIVIDIR 9 entre Sobrn 9 persons grupos de 0 persons utobuses Necesitmos otro utobús TOTAL: 7 utobuses un utobús con 9 persons y utobuses completos En el utobús de 9 persons hy sientos libres Cuántos? DIFERENCIA entre sientos que hy y sientos ocupdos 0 9 sientos libres.. El utobús que hce el recorrido de Murci Mdrid slió de l estción con treint y dos psjeros. En Albcete bjron ocho psjeros y subieron veinte. Al llegr Mot del Cuervo subieron cutro psjeros más. Si no hubo otr prd, cuánts persons llegron Mdrid? psjeros persons dentro del utobús Subir Dtos En Murci psjeros En Albcete bjn 8 psjeros suben 0 psjeros Bjr 7
31 En Mot del Cuervo suben psjeros Pregunt En Mdrid psjeros? Operción Debes sber: Si SUBEN psjeros hy MÁS psjeros SUMAR Si BAJAN psjeros hy MENOS psjeros RESTAR En Murci psjeros En Albcete: bjn 8 persons en el utobús hor - 8 psjeros suben 0 persons en el utobús hor + 0 psjeros En Mot del Cuervo: suben persons en el utobús hor + 8 psjeros No hy más prds entonces en Mdrid bjron 8 persons. 7. En cierto supermercdo sbemos que el kilo de ptts cuest, el kilo de plátnos cuest y el kilo de queso cuest 9. Si comprmos kilos de ptts, kilos de plátnos y kilo de queso, cuánto nos cobrron? Si tenemos 0, cuánto nos sobrrá? kilo de ptts vle kilo de plátnos vle kilo de queso vle 9 Dtos Compro Kg. de ptts Compro Kg. de plátnos Compro Kg. de queso Yo tengo 0 Todo JUNTO vle? Sobr? Pregunt Operción JUNTAR lo que vlen Kg. de ptts, Kilos de plátnos y Kg. de queso Kg. de ptts vlen VECES lo que vle Kg. de ptts Kilos de plátnos vlen VECES lo que vle Kg. de plátnos Kg. de queso 9 TODO JUNTO vle SUMAR lo que vlen Kg. de ptts, Kilos de plátnos y Kg. de queso Yo tengo 0 > entonces SOBRA SOBRA DIFERENCIA del dinero que tengo menos el dinero que pgo 0 sobrn 8
32 PROBLEMAS PROPUESTOS 9
33 . Escribe como se dicen los siguientes números: ) 7 e) 0 i) 0000 b) f) 7 j) 897 c) 8 g) 00 k) 899 d) 89 h) 7 l) Escribe los siguientes números: ) Seiscientos curent y tres mil veinticinco b) Un millón cutrocientos veintisiete mil seis c) Ciento veinticinco d) Dos millones quinientos veintitrés e) Novecientos sesent y ocho mil nueve Represent dibuj. Represent sobre un rect los números:,, 7,,,. Qué orden tienen estos números?. Coloc entre cd pr de números los signos de desiguldd (> o <): ) y < b) y c) 0 y 7 d) 7 y 8 e) 7 y 8 f) 0 y 0 cifrs en este ejemplo l sum de ls tres cifrs es + +. Complet: ) 7 centens, decens y 7 uniddes b) c) 77 d) e) f) 0000 g) 0. ) Orden los siguientes números de menor myor: 7,, 8,,,,.0. b) Orden los siguientes números de myor menor:,,, 7, 8,. 7. Escribe cinco números de tres cifrs pr que l sum de ests cifrs se quince. 8. Escribe cinco números de tres cifrs pr que l sum de ls uniddes y ls decens se doce. 9. Escribe cinco números de cutro cifrs pr que ls uniddes de millr y ls decens sumen trece. 0
34 0. Efectú ls siguientes operciones: Reliz ls siguientes operciones: ) 7 09 b) c) 0 8 d) 9 9 e) En unos grndes lmcenes observmos los siguientes precios: un cmis 0, un pr de zptos 8, un bolso, un toll, un reloj y uns gfs de sol 0. Indic cuánto me he gstdo en cd uno de los csos siguientes: ) Si compro un cmis y un bolso. b) Si compro un toll, un reloj y uns gfs de sol. c) Si compro un pr de zptos, un cmis y un bolso. grndes lmcenes tiend grnde. Quiero hcer el siguiente vije: Primer dí: De Murci Vlenci (70 Km.) Segundo dí: De Vlenci Mdrid (00 Km.) Trs psr en Mdrid vrios dís regreso de Mdrid Murci (0 Km.) Cuántos Km. he recorrido en este vije?. En el ño.978 comenzó construirse un instituto, ños después se cbó. En qué ño se terminó el instituto? oso prdo. An tiene y su mdre le d en el fin de semn. Cuántos tiene hor An?. En un piscin hy.000 litros de gu y ñdimos.00 litros. Cuántos litros hy hor en l piscin? oso polr 7. En un zoo hy osos prdos, osos polres y osos pnd Cuántos osos hy en el zoo? 8. Crolin h gstdo en el utobús, en comer y en el cine. Cuánto dinero h gstdo Crolin? 9. En un bosque hy pinos. Plntn pinos más, cuántos pinos hy hor? 0. L mdre de Luis tiene un docen de huevos y utiliz huevos pr hcer un tortill, cuántos le quedn?. Mri Trini tiene ños y Melis 9. Quién es myor? qué diferenci de edd hy? oso pnd un docen de huevos huevos
35 . Mrí pes kilos y Loli 0 kilos, quién pes más? Cuál es l diferenci de peso?. Hce ños que compré un cs. Si estmos en el ño.00 en qué ño compré l cs?. Alici tiene 0. Yo tengo menos que Alici, Cuántos euros tengo yo? álbum de fotos álbum dentro fotos. Angel tiene un álbum con fotos. En el álbum cben 00 fotos y Angel tiene y 8, cuánts le fltn pr completr el álbum?. En el ul de ºC hy 0 mess. Hoy hy mess vcís, cuántos lumnos hy en clse? rrncr quitr 7. En un bosque de 0 pinos rrncn, cuántos pinos quedn? 8. En un prque quieren poner sientos. Se hn colocdo y 9 sientos, cuántos fltn por poner? 9. En un excursión que los lumnos de º E hn hecho l ply se hn bñdo 8 lumnos. Si l excursión hn ido 7 lumnos, cuántos lumnos no se hn bñdo? 0. Jun compr dulces, por el cmino se come, cuántos dulces le quedn? tbleros. Tenemos un tblero de 0 cm. de lrgo y 0 cm. de ncho, cuánto debo cortrle de lrgo y de ncho pr conseguir un tblero de 0 cm. de lrgo y 0 de ncho?. Clcul el doble de: ) b) c)7. Clcul el triple de: ) b)7 c)0 hombre cortndo un tblero. Clcul l mitd de: ) b) c)90. Mrí tiene 0 ños y su mdre tiene el triple, cuántos ños tiene su mdre?. Lucí tiene 0 y le d l mitd su mrido, cuánto dinero le d? 7. Jun tiene 0 juegos de ordendor y Mrí tiene el doble de juegos, cuántos juegos tiene Mrí? 8. Si un litro de vino cuest, cuánto me costrán litros de vino?
36 9. Tengo montones de moneds y en cd montón tengo 0 moneds, cuánts moneds tengo? 0. En un huerto hy 0 fils de nrnjos y en cd fil hy 7 nrnjos, cuántos nrnjos hy en el huerto?. Un estnterí tiene lejs. Cd lej tiene libros, Cuántos libros hy en l estnterí?. Tengo botells de gu. Cd botell es de litros, cuántos litros de gu tengo? montón de moneds. En un edificio hy plnts, en cd plnt hy pisos, cuántos pisos hy en dicho edificio?. Si cd cj de cerills tiene 00 cerills y tengo 8 cjs de cerills, Cuánts cerills tengo? cj de cerills. Abrhm tiene cjs de lápices con 0 lápices cd cj. Cuántos lápices tiene Abrhm?. Cuántos dís son semns? 7. ) Cuánts pts tienen cbllos? b) Cuánts pts tienen pollos y 0 cerdos? 8. persons quieren ir l ply en coche. Si en cd coche cben persons, cuántos coches necesitremos? 9. Mrí tiene crmelos que quiere reprtir prtes igules entre sus 7 migs. Cuántos crmelos d cd mig?, cuántos le sobrn? 0. migos slen l cine y cenr. En totl se gstn, cuántos euros h gstdo cd uno?. L profesor de mtemátics nos h puesto 0 problems pr hcerlos en dís, cuántos problems debo hcer cd dí?. Un álbum de fotos tiene 0 págins. Si tengo fotos y en cd págin cben fotos, Me cben tods ls fotos en este álbum? Cuánts págins ocupré?. En un hotel hy limpidors y 0 hbitciones. Cuánts hbitciones tiene que limpir cd limpidor? limpidors mujer que trbj limpimdo. En un clle de 0 metros de lrg queremos prcr coches. Si cd coche necesit metros: ) Cuántos coches puedo prcr? b) Cuántos metros me sobrn?
37 . Un grupo de 9 migos deciden coger en l ply uns brcs. En cd brc cben persons. ) Cuánts brcs deben lquilr? b) Si el precio del lquiler de cd brc es de, cuánto le costrá cd uno de los migos?. Cuántos dís son 7 semns y dís? cnics 7. En un prtid con cnics, Jun empezó con 7 cnics. En l primer prtid perdió cnics, en l segund gnó cnics, en l tercer gnó y en l curt prtid ni gnó ni perdió. Con cuántos cnics cbó Jun ls prtids? 8. Jun tiene tres hermnos y yo tengo el doble de hermnos que Jun. Cuántos hermnos tengo yo? 9. Complet l siguiente fctur: rmrio de mder pts mes de comedor de 0.90 x pts Recuerd: hor tiene 0 minutos minuto tiene 0 segundos. sills de comedor de mder.000 pts./unidd... TOTAL A PAGAR Cuántos segundos tiene un dí?. L sum de tres números es.7; los dos primeros sumn 7.0 y el segundo es.9. Qué números son?. Un cmión trnsport 9 scos de trigo de 8 kilos cd uno y 7 scos de rroz de kilos cd uno. Cuánto peso llev? sco de trigo. 9 Kg. de cfé me hn costdo 7. Cuánto dinero costrán kilos de cfé?
38 SOLUCIONES. ) veintisiete b) treint y uno c) ciento veintiocho d) ochocientos novent y cutro e) mil veintitrés f) cinco mil cutrocientos setent y uno g) seis mil seis h) setent y tres mil cutrocientos veinticinco i) ciento cincuent mil j) cutrocientos cincuent y ocho mil novecientos setent y cinco k) dos millones ochocientos curent y nueve mil cutrocientos novent y cinco l) cutro millones quinientos sesent y siete mil ochocientos novent.. ) 0 b) 7 00 c) d) 000 e) < < < < < ) y < b) y > c) 0 y 7 0 < 7 d) 7 y 8 7 > 8 e) 7 y 8 7 < 8 f) 0 y 0 0 < 0. ) 7 centens, decens y 7 uniddes b) uniddes de millr, centens, decens y un unidd c) 77 7 uniddes de millr, centens, 7 decens y uniddes d) unidd de millr, centens, decens y uniddes e) centen, decens y uniddes f) unidd de millón, centens de millr y uniddes g) 0 unidd de millr, decens y uniddes. ) < 7 < < 8 < < <.0. b) 8 > > 7 > > >. 7. 9, 9, 8,,. 8., 7, 8,, , 70, 8, 900, ) 7 09 b) c) d) e) ) b) 0 c) Km.. El instituto se terminó en litros osos pinos huevos.. Es myor Mri Trini. L diferenci es de ños.. Pes más Mrí. L diferenci es de kilos.. En fotos.. lumnos pinos. 8. sientos lumnos no se hn bñdo dulces.. Hy que cortr 0 cm. de lrgo y 0 cm. de ncho.
39 . ) 8 b).8 c) 9. ) 8 b) 0 c) 80. ) 7 b) 8 c). 0 ños juegos moneds nrnjos.. litros.. 80 litros.. pisos cerills.. 0 lápices.. 8 dís. 7. ) pts b) 90 pts. 8. coches. 9. D 7 crmelos cd mig y le sobrn crmelos gst cd uno.. problems cd dí.. Sí cben tods ls fotos, necesitré págins.. hbitciones cd limpidor.. ) 7 coches b) metros.. ) brcos b) pg cd person.. dís 7. 8 cnics. 8. Seis hermnos. 9. rmrio de mder de pino pts. mes de comedor de 0.90 x pts. sills de comedor de pino.000 pts./unidd pts. TOTAL A PAGAR pts segundos. El primer número es y el tercero es kilos...
40 TEMA II: LOS NÚMEROS ENTEROS Autores: José Luis Cmcho Nvs Mª Belén Rmírez Hellín 7
41 TEXTO ADAPTADO sótno pisos bjo tierr. Ejemplo: grje de coches en El Corte Inglés 0º LOS NÚMEROS ENTEROS Los números nturles no vlen pr tods ls situciones de l vid. Por ejemplo seguro tú hs visto un scensor. El scensor tiene números negtivos (-), por ejemplo -, -, - que quiere decir sótnos de un edificio; l tempertur tmbién puede ser negtiv, ejemplo -0º, -º, -º, que quiere decir "menos de 0". Los números nturles no vlen pr eso, necesitmos otros números: los números enteros. El conjunto de números enteros se llm Z y son los números 0,, -,, -,, -... Z {..., -, -, -, -, 0,,,,,...} Los números como y - o y - o 7 y -7 son igules pero tienen distinto signo: se dice que son opuestos. los números -, -, -,... se llmn números negtivos y los números,,,... se llmn números positivos. Los números negtivos se leen: - menos uno - menos dos... En el tem nterior y hemos dibujdo los números nturles en un rect. Ahor podemos hcer igul con los números enteros. Los números negtivos quiere decir psos l izquierd del 0 y positivos quiere decir psos l derech del 0. Ejemplo: pr dibujr número, hcemos psos l derech del 0 0 y pr dibujr número, contr psos l izquierd del 0. psos - 0 Grcis l dibujo, podemos ordenr los números, igul que ntes con los números nturles. Pr ordenr números -7, -,, - y : primero dibujr en un rect y hor leer de izquierd derech ( ): < se dice menor que > se dice myor que se dice - 7 después - después - después después - 7 < - < - < < - 7 menor que - menor que - menor que menor que 8
42 LOS NÚMEROS ENTEROS Con los números nturles no podemos describir tods ls situciones que se presentn en l vid diri. Así, por ejemplo, puede que en un scensor vemos los números -, -, - pr indicr los sótnos de un edificio o que l decir l tempertur de un determindo lugr nos dign que hy -0º. Pr resolver situciones como ésts se utilizn los números enteros que se representn por Z y son 0,, -,, -,, -,... A los números -, -, -,... se les llm números negtivos y los números,,,... se les llm números positivos. Z {..., -, -, -, -, 0,,,,,...} Los números como y - o y - o 7 y -7 que son igules pero con distinto signo se dice que son opuestos. Igul que representmos sobre un rect los números nturles, tmbién podemos representr sobre un rect los números enteros. El proceso será el mismo pero si el número es negtivo contremos desde cero hci l izquierd y si es positivo de cero hci l derech. Por ejemplo, pr representr el número mediremos tres uniddes l derech del cero 0 y pr representr el número - mediremos tres uniddes de longitud l izquierd del cero. - 0 A prtir de est representción podemos ordenr un serie de números igul que lo hcímos en los números nturles. Así, pr ordenr los números -7, -,, - y los representremos sobre un rect y hor leemos de izquierd derech: - 7 después - después - después después - 7 < - < - < < que se lee - 7 menor que - menor que menor que menor que 9
43 TEXTO ADAPTADO Recuerd que: número sin signo número positivo ejemplo: + OPERACIONES CON NÚMEROS ENTEROS SUMA: Pr sumr dos números enteros primero mir el signo. Cundo los dos números tienen el mismo signo, (+ + ó - -) primero sumr los números y después copir el signo. Ejemplos: + positivo positivo se sumn (+) y se pone el signo + (-) + (-) - negtivo negtivo se sumn (+) y se pone el signo - Cundo los dos números tienen signo distinto (+ -), primero se restn los números (número grnde número pequeño) y después poner el signo del número grnde. Ejemplos: () + (-) - positivo negtivo se restn (- ) signo? mismo del número grnde - (negtivo) () + (-) - (-) + negtivo positivo se restn (-) signo? mismo del número grnde + (positivo) (-) + + Otros ejemplos: + (-) ; (-7) + 9 ; 7 + (-0) - Pr sumr vrios números, se sumn seprdos en grupos; se hce un grupo con números positivos y un grupo con números negtivos. Después restr grupo grnde menos (-) grupo pequeño, signo? el mismo del grupo grnde. Ejemplo: + (-) + + (-) (-8) Grupo positivos:,, y l sum es Grupo negtivos: (-), (-) y (-8) su sum es (-) Ahor restr los dos grupos - y signo el mismo del grupo grnde: + + (-) + + (-) (-8) + (-) + Vmos clculr hor (-) + (-7) + + (-8) (-) (-) + (-7) + + (-8) (-) + (-) -8 0
44 OPERACIONES CON NÚMEROS ENTEROS SUMA: Pr sumr dos números enteros nos fijremos primero en su signo. Si los dos números tienen igul signo, sumremos los números sin tener en cuent el signo y copiremos el signo. Ejemplos: ) + los números sumr son y que son mbos positivos, entonces los sumremos y pondremos l resultdo el signo positivo. b) (-) + (-) - los números sumr son (-) y (-) que son mbos negtivos, entonces los sumremos y pondremos l resultdo el signo negtivo. Si los dos números tienen distinto signo, restremos los números sin tener en cuent el signo (el myor menos el menor) y pondremos el signo del myor. Ejemplos: ) () + (-) - los números sumr son y (-) que tienen distinto signo, es positivo y (-) es negtivo por tnto, restremos sin considerr los signos. Si no considermos los signos, es myor que luego restmos menos que d. Como el myor (sin signo) es que viene de quitr el signo (-) que es negtivo el resultdo será negtivo. b) (-) + los números sumr son (-) y que tienen distinto signo, (-) es negtivo y es positivo por tnto, restremos sin considerr los signos. Si no considermos los signos, es myor que luego restmos menos que d. Como el myor (sin signo) es que viene de que es positivo el resultdo será positivo. Otros ejemplos: + (-) ; (-7) + 9 ; 7 + (-0) - Si lo que queremos es sumr vrios números, sumremos por un prte todos los positivos y por otr todos los negtivos. Después restremos estos dos resultdos poniendo el signo del myor. Ejemplos: ) + (-) + + (-) (-8) los números positivos son,, y y su sum es los números negtivos son (-), (-) y (-8) y su sum es (-) Ahor restmos los dos resultdos sin signo - ponemos el signo del myor que es positivo. + (-) + + (-) (-8) + (-) b) Vmos clculr hor (-) + (-7) + + (-8) (-) (-) + (-7) + + (-8) (-) + (-) -8
45 TEXTO ADAPTADO Recuerd que: número opuesto cmbir signo Ejemplos: opuesto - opuesto +... RESTA: Restr dos números enteros Cómo se hce?: Primer número + opuesto del segundo número Ejemplos: ) opuesto (-), entonces: + (-) - b) - (-) (-) opuesto, entonces: - (-) + Otros ejemplos: (-) - (-) (-) + (-) - 8 (-) + (-8) - Cundo hy vris sums y rests, primero cmbir todo sums y después hcer igul que el ejemplo de rrib. Ejemplos: ) Pr hcer (-) ( -) + (-) - (-9) + cmbir rests sums: (-) - 8 -(-) + (-) -(-9) + (-) +(-8) +() + (-) + (9) + hcer l sum (-) + (-8) + () + (-) + (9) + y hor sumr cd grupo, los positivos en un grupo y los negtivos en otro grupo: (-) + (-8) + () + (-) + (9) + + (-) b) Ahor vmos clculr: (-) PRODUCTO MULTIPLICA- CIÓN (-) + (-) + + (-8) (-0) + () + (-) + + (-8) (-0) + () + (-) - PRODUCTO: Pr multiplicr dos números enteros, primero multiplicr los números sin signo y después multiplicr signos. Cómo? Hy ests regls: Regl L regl quiere decir Ejemplo Positivo x positivo positivo (+) (+ ) (+) negtivo x negtivo positivo (-) (- ) (+) positivo x negtivo negtivo (+) (- ) (-) negtivo x positivo negtivo (-) (+ ) (-) Otros ejemplos: (-) (-8) (+); (-) (-0) prte seprdo, en otro sitio Pr multiplicr vrios números, multiplicr primero todos los números y prte multiplicr los signos. Ejemplo: Multiplicr (-) (-) (-): primero el producto de números, sin signo: 0 y después multiplicr signos: Entonces l solución de (-) (-) (-) - 0
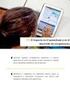
Los números enteros y racionales
 Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Desarrollos para planteamientos de ecuaciones de primer grado
 1) Hllr un número tl que su triple menos 5 se igul su doble más 2. 5= 2 + 2 2= 2+ 5 = 7 2) El triple de un número es igul l quíntuplo del mismo menos 20. Cuál es este número? = 5 20 20 = 5 20 = 2 = 10
1) Hllr un número tl que su triple menos 5 se igul su doble más 2. 5= 2 + 2 2= 2+ 5 = 7 2) El triple de un número es igul l quíntuplo del mismo menos 20. Cuál es este número? = 5 20 20 = 5 20 = 2 = 10
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN
 http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
 Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
TEMA 1. LOS NÚMEROS REALES
 TEMA. LOS NÚMEROS REALES. Operciones con números nturles. Los números nturles son los que se utilizn pr contr 0,,,,,, Con los números nturles podemos relizr diferentes operciones, como - Sum + = 8 - Rest
TEMA. LOS NÚMEROS REALES. Operciones con números nturles. Los números nturles son los que se utilizn pr contr 0,,,,,, Con los números nturles podemos relizr diferentes operciones, como - Sum + = 8 - Rest
MATRICES DE NÚMEROS REALES
 MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
Máximo común divisor. 2. Descomposición en primos Ejemplo. Encontrar mcd 504,300 Se descomponen ambos números en primos 504 2 252 2 126 2 63 3 21 3
 Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
1. Cuales son los números naturales?
 Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Curso ON LINE Tema 5. x + y + z = 5 1200x + 600y = 2000 + m z 1200x = 3 m z
 Curso ON LINE Tem 5 Un gente inmobilirio puede relir tipos de operciones: vent de un piso nuevo, vent de un piso usdo lquiler. Por l vent de cd piso nuevo recibe un prim de. Si l operción es l vent de
Curso ON LINE Tem 5 Un gente inmobilirio puede relir tipos de operciones: vent de un piso nuevo, vent de un piso usdo lquiler. Por l vent de cd piso nuevo recibe un prim de. Si l operción es l vent de
a n =b Si a es múltiplo de b, entonces b es divisor de a. Números primos: son números cuyos únicos divisores son ellos mismos y el 1.
 1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
7Soluciones a los ejercicios y problemas PÁGINA 161
 7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
a) Decimales finitos: Corresponden a los cuocientes exactos entre el numerador y el denominador. Ejemplo: : 8 = (b)
 Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
IES CINCO VILLAS TEMA 8 ALGEBRA Página 1
 SOLUCIONES MÍNIMOS CURSO º ESO TEMA 8 ALGEBRA Ejercicio nº.- Epres de form lgeric los siguientes enuncidos mtemáticos: ) El triple de sumr siete un número, n. El número siguiente l número nturl. c) El
SOLUCIONES MÍNIMOS CURSO º ESO TEMA 8 ALGEBRA Ejercicio nº.- Epres de form lgeric los siguientes enuncidos mtemáticos: ) El triple de sumr siete un número, n. El número siguiente l número nturl. c) El
En general, si. son números racionales, la suma es un número racional.
 ... SUMA DE FRACCIONES. Al relizr sums con números rcionles encontrmos csos muy específicos, como son los siguientes: Sum de números rcionles con el mismo denomindor. Pr resolver este tipo de ejercicios
... SUMA DE FRACCIONES. Al relizr sums con números rcionles encontrmos csos muy específicos, como son los siguientes: Sum de números rcionles con el mismo denomindor. Pr resolver este tipo de ejercicios
Unidad 2. Fracciones y decimales
 Mtemátics Múltiplo.º ESO / Resumen Unidd Unidd. Frcciones y decimles FRACCIONES NÚMEROS DECIMALES EXPRESIÓN, 8, 9 SIGNIFICADO FRACCIONES EQUIVALENTES 0 30 0 0 Prte de un unidd Prte de un cntidd ORDENACIÓN
Mtemátics Múltiplo.º ESO / Resumen Unidd Unidd. Frcciones y decimles FRACCIONES NÚMEROS DECIMALES EXPRESIÓN, 8, 9 SIGNIFICADO FRACCIONES EQUIVALENTES 0 30 0 0 Prte de un unidd Prte de un cntidd ORDENACIÓN
Cálculo del valor decimal de una fracción Para obtener el valor de una fracción se divide el numerador entre el denominador. 2 5
 LECCIÓN : FRACCIONES.- QUÉ ES UNA FRACCIÓN? UNA FRACCIÓN ES...... L epresión un prte un cntidd enter. Términos un frcción: DENOMINADOR: Es el número que se coloc bjo l r frcción e indic el número totl
LECCIÓN : FRACCIONES.- QUÉ ES UNA FRACCIÓN? UNA FRACCIÓN ES...... L epresión un prte un cntidd enter. Términos un frcción: DENOMINADOR: Es el número que se coloc bjo l r frcción e indic el número totl
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA
 EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
4 FRACCIONES INTRODUCCIÓN A LAS FRACCIOES. FRACCIONES EQUIVALENTES COMPARACIÓN DE FRACCIONES. REDUCCIÓN A COMÚN DENOMINADOR
 FRACCIONES..- INTRODUCCIÓN A LAS FRACCIOES. FRACCIONES EQUIVALENTES...- COMPARACIÓN DE FRACCIONES. REDUCCIÓN A COMÚN DENOMINADOR..- OPERACIONES CON FRACCIONES (I)..- OPERACIONES CON FRACCIONES (II)..-
FRACCIONES..- INTRODUCCIÓN A LAS FRACCIOES. FRACCIONES EQUIVALENTES...- COMPARACIÓN DE FRACCIONES. REDUCCIÓN A COMÚN DENOMINADOR..- OPERACIONES CON FRACCIONES (I)..- OPERACIONES CON FRACCIONES (II)..-
Sistemas de ecuaciones lineales
 Sistems de ecuciones lineles º) L sum de ls tres cifrs de un número es 8, siendo l cifr de ls decens igul l medi de ls otrs dos. Si se cmbi l cifr de ls uniddes por l de ls centens, el número ument en
Sistems de ecuciones lineles º) L sum de ls tres cifrs de un número es 8, siendo l cifr de ls decens igul l medi de ls otrs dos. Si se cmbi l cifr de ls uniddes por l de ls centens, el número ument en
TEMA 1: FUNCIONES. LÍMITES Y CONTINUIDAD
 Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
INFORME DE LA PRÁCTICA nº 2: LA RUEDA DE MAXWELL. Fernando Hueso González. Carlos Huertas Barra. (1º Fís.), L1, 21-XI-07 - 0 -
 INFORME DE LA PRÁCTICA nº : LA RUEDA DE MAXWELL Fernndo Hueso González. Crlos Huerts Brr. (1º Fís.), L1, 1-XI-7 - - RESUMEN L práctic de l rued de Mxwell consiste en medir el tiempo que trd en descender
INFORME DE LA PRÁCTICA nº : LA RUEDA DE MAXWELL Fernndo Hueso González. Crlos Huerts Brr. (1º Fís.), L1, 1-XI-7 - - RESUMEN L práctic de l rued de Mxwell consiste en medir el tiempo que trd en descender
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Módulo 12 La División
 Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
1. Definición. Formas de definir una sucesión.
 . Definición. Forms de definir un sucesión. Un sucesión es un plicción que nos relcion los números nturles con un conjunto, de form que orden los elementos de tl conjunto. Ejemplos:. : selección espñol
. Definición. Forms de definir un sucesión. Un sucesión es un plicción que nos relcion los números nturles con un conjunto, de form que orden los elementos de tl conjunto. Ejemplos:. : selección espñol
PROBLEMAS DE OPTIMIZACIÓN
 PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
1 Completa los huecos con el artículo el o con el pronombre personal él, según sea el caso.
 1 Complet los huecos con el rtículo el o con el pronombre personl él, según se el cso. me dijo que compró libro yer. b coche de Fernndo er de un color que sólo le gustb. c rte de Pblo Picsso es un de ls
1 Complet los huecos con el rtículo el o con el pronombre personl él, según se el cso. me dijo que compró libro yer. b coche de Fernndo er de un color que sólo le gustb. c rte de Pblo Picsso es un de ls
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
1Soluciones a los ejercicios y problemas
 Soluciones los ejercicios y problems ) 8 : 8 ) 8 8 : ) 8 8 : Pág PÁGINA 8 Clcul y comprueb con l clculdor ) ) : : ) ) ) 8 [ 0 )] ) ) : ) [ 0 ] : : 0 88 8 ) ) ) 8 [ ) 0) : ) ] : ) 8 8 Reduce un frcción
Soluciones los ejercicios y problems ) 8 : 8 ) 8 8 : ) 8 8 : Pág PÁGINA 8 Clcul y comprueb con l clculdor ) ) : : ) ) ) 8 [ 0 )] ) ) : ) [ 0 ] : : 0 88 8 ) ) ) 8 [ ) 0) : ) ] : ) 8 8 Reduce un frcción
NÚMEROS RACIONALES. Los números racionales son todos aquellos números de la forma b
 NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
Ecuaciones de 1 er y 2º grado
 Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 3 1. NÚMEROS RACIONALES UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números
C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 3 1. NÚMEROS RACIONALES UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números
CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS
 CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS ACTIVIDAD ACADEMICA: LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD
CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS ACTIVIDAD ACADEMICA: LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD
Tema9. Sucesiones. Tema 9. Sucesiones.
 Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
RESUMEN 01 NÚMEROS. Nombre : Curso. Profesor :
 RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
Guía de Trabajo n 1 Octavo año básico Refuerzo Contenido y Aprendizaje N. Cero (restitución de aprendizajes) Números
 Colegio Antil Mwid Deprtmento de Mtemátic Profesor: Nthlie Sepúlved Guí de Trjo n Octvo ño ásico Refuerzo Contenido y Aprendizje N Fech Tiempo 2 Hors Nomre del/l lumno/ Unidd Nº Núcleos temáticos de l
Colegio Antil Mwid Deprtmento de Mtemátic Profesor: Nthlie Sepúlved Guí de Trjo n Octvo ño ásico Refuerzo Contenido y Aprendizje N Fech Tiempo 2 Hors Nomre del/l lumno/ Unidd Nº Núcleos temáticos de l
NÚMEROS RACIONALES Y DECIMALES
 NÚMEROS RACIONALES Y DECIMALES Unidad didáctica. Números racionales y decimales CONTENIDOS Fracciones Fracciones equivalentes Amplificar fracciones Simplificar fracciones Representación en la recta numérica.
NÚMEROS RACIONALES Y DECIMALES Unidad didáctica. Números racionales y decimales CONTENIDOS Fracciones Fracciones equivalentes Amplificar fracciones Simplificar fracciones Representación en la recta numérica.
DIVERSIFICACIÓN CURRICULAR
 ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
2 cuando a y b toman los valores 2 y -1,
 COLEGIO PEDAGÓGICO DE LOS ANDES TALLER DE NIVELACIÓN DE MATEMÁTICAS SEGUNDO PERIODO GRADO OCTAVO ALGEBRA...- - LLeenngguuj jjee l llggee ri r iiccoo El lenguje numérico sirve pr epresr operciones en ls
COLEGIO PEDAGÓGICO DE LOS ANDES TALLER DE NIVELACIÓN DE MATEMÁTICAS SEGUNDO PERIODO GRADO OCTAVO ALGEBRA...- - LLeenngguuj jjee l llggee ri r iiccoo El lenguje numérico sirve pr epresr operciones en ls
Unidad 1 números enteros 2º ESO
 Unidad 1 números enteros 2º ESO 1 2 Conceptos 1. Concepto de número entero: diferenciación entre número entero, natural y fraccionario. 2. Representación gráfica y ordenación. 3. Valor absoluto de un número
Unidad 1 números enteros 2º ESO 1 2 Conceptos 1. Concepto de número entero: diferenciación entre número entero, natural y fraccionario. 2. Representación gráfica y ordenación. 3. Valor absoluto de un número
Sistemes d equacions (Gauss)
 Sistemes d equcions (Guss) Ejercicio nº.- Dos kilos de nrnjs, más un kilo de plátnos, más dos kilos de mngos, vlen, euros. Dos kilos de nrnjs, más dos kilos de plátnos, más de mngos, vlen euros. Tres kilos
Sistemes d equcions (Guss) Ejercicio nº.- Dos kilos de nrnjs, más un kilo de plátnos, más dos kilos de mngos, vlen, euros. Dos kilos de nrnjs, más dos kilos de plátnos, más de mngos, vlen euros. Tres kilos
C.A.R.E.I. Centro Aragonés de Recursos para la Educación Intercultural Documento facilitado por Grupo de Trabajo de CPR Huesca 1.
 1.º PRIMARIA AREA DE MATEMÁTICAS Concepto de número. Cálculo mental El evaluador, lee el problema y anota la respuesta. El niño lo debe resolver mentalmente, contando o no con los dedos se anotará si lo
1.º PRIMARIA AREA DE MATEMÁTICAS Concepto de número. Cálculo mental El evaluador, lee el problema y anota la respuesta. El niño lo debe resolver mentalmente, contando o no con los dedos se anotará si lo
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES
 TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Ejercicios. Números enteros, fraccionarios e irracionales.
 CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
CONSIDERACIONES SOBRE LAS COMPUERTAS
 Abril de 006 CONSDERACONES SOBRE LAS COMPUERTAS Cátedr de Mecánic de los Fluidos Escuel de ngenierí Mecánic Autores: ngeniero Edgr Blbstro ngeniero Gstón Bourges e-mil: gbourges@fcei.unr.edu.r 1 Abril
Abril de 006 CONSDERACONES SOBRE LAS COMPUERTAS Cátedr de Mecánic de los Fluidos Escuel de ngenierí Mecánic Autores: ngeniero Edgr Blbstro ngeniero Gstón Bourges e-mil: gbourges@fcei.unr.edu.r 1 Abril
Introducción. Objetivos de aprendizaje. Determinar las propiedades de las operaciones de números racionales
 L rect numéric, un cmino l estudio de los números reles Deducción de propieddes en ls operciones de números rcionles Introducción 0,1 1/ / 0,0 Multiplic por Rest 0, 1/ /7 1/ Figur 1. Rulet Objetivos de
L rect numéric, un cmino l estudio de los números reles Deducción de propieddes en ls operciones de números rcionles Introducción 0,1 1/ / 0,0 Multiplic por Rest 0, 1/ /7 1/ Figur 1. Rulet Objetivos de
TEMA 1: ACTIVIDADES Y AUTOEVALUACIONES RESUELTAS
 MÓDULO - Ámbito Científico-Tecnológico TEMA : ACTIVIDADES Y AUTOEVALUACIONES RESUELTAS Actividd p.: Clcul el vlor numérico de ls siguientes epresiones lgebrics pr los vlores de ls letrs que se indicn:
MÓDULO - Ámbito Científico-Tecnológico TEMA : ACTIVIDADES Y AUTOEVALUACIONES RESUELTAS Actividd p.: Clcul el vlor numérico de ls siguientes epresiones lgebrics pr los vlores de ls letrs que se indicn:
Conjuntos numéricos. Intervalos. Operaciones en el conjunto de números reales.
 Fich Técnic Conjuntos numéricos Intervlos Operciones en el conjunto de números reles Índice de tems: Conjuntos numéricos Intervlos Operciones y propieddes Módulo o vlor bsoluto de un número rel Conjuntos
Fich Técnic Conjuntos numéricos Intervlos Operciones en el conjunto de números reles Índice de tems: Conjuntos numéricos Intervlos Operciones y propieddes Módulo o vlor bsoluto de un número rel Conjuntos
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS
 TABLA DE DISTRIBUCIÓN DE FRECUENCIAS L.C. y Mtro. Frncisco Jvier Cruz Ariz L.C. y Mtro. Frncisco Jvier Cruz Ariz TABLA DE DISTRIBUCIÓN DE FRECUENCIAS Un mner de simplificr los dtos es usr un tbl de frecuenci
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS L.C. y Mtro. Frncisco Jvier Cruz Ariz L.C. y Mtro. Frncisco Jvier Cruz Ariz TABLA DE DISTRIBUCIÓN DE FRECUENCIAS Un mner de simplificr los dtos es usr un tbl de frecuenci
UNIDAD 8.- Determinantes (tema 2 del libro)
 UNIDD 8.- Determinntes (tem del libro). DETERMINNTES DE ORDEN Y Definición: Pr un mtriz cudrd de orden, por det( ) ó, l siguiente nº rel: det( ) Definición: Pr un mtriz cudrd de orden, not por det( ) ó,
UNIDD 8.- Determinntes (tem del libro). DETERMINNTES DE ORDEN Y Definición: Pr un mtriz cudrd de orden, por det( ) ó, l siguiente nº rel: det( ) Definición: Pr un mtriz cudrd de orden, not por det( ) ó,
Universidad Central de Venezuela Facultad de Farmacia Matemática - Física Prof. J. R. Morales
 Universidd Centrl de Venezuel Fcultd de Frmci Mtemátic - Físic Prof J R Morles Guí de Vectores (Resumen de l Teorí) 1 En físic distinguiremos dos tipos de cntiddes: vectoriles esclres Ls cntiddes vectoriles
Universidd Centrl de Venezuel Fcultd de Frmci Mtemátic - Físic Prof J R Morles Guí de Vectores (Resumen de l Teorí) 1 En físic distinguiremos dos tipos de cntiddes: vectoriles esclres Ls cntiddes vectoriles
OBJETIVOS: - Construir números utilizando correctamente los conceptos de unidad, decena y centena. - Establecer relaciones de orden y cantidad entre
 1 OBJETIVOS: - Construir números utilizando correctamente los conceptos de unidad, decena y centena. - Establecer relaciones de orden y cantidad entre los números. - Identificar los términos de la suma
1 OBJETIVOS: - Construir números utilizando correctamente los conceptos de unidad, decena y centena. - Establecer relaciones de orden y cantidad entre los números. - Identificar los términos de la suma
NÚMEROS Y OPERACIONES
 NÚMEROS Y OPERACIONES NUESTRO SISTEMA DE NUMERACIÓN Para escribir un número usamos sólo diez cifras, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 El número 2 1 403.745 está formado por siete órdenes de unidades.
NÚMEROS Y OPERACIONES NUESTRO SISTEMA DE NUMERACIÓN Para escribir un número usamos sólo diez cifras, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 El número 2 1 403.745 está formado por siete órdenes de unidades.
Apoyo compartido. Matemática Período 1 CUADERNO DE TRABAJO BÁSICO
 Apoyo comprtido Mtemátic Período CUADERNO DE TRABAJO 3º BÁSICO DOB MIT Cuderno de trbjo Mtemátic 3º Básico, Período NIVEL DE EDUCACIÓN BÁSICA División de Educción Generl Ministerio de Educción Repúblic
Apoyo comprtido Mtemátic Período CUADERNO DE TRABAJO 3º BÁSICO DOB MIT Cuderno de trbjo Mtemátic 3º Básico, Período NIVEL DE EDUCACIÓN BÁSICA División de Educción Generl Ministerio de Educción Repúblic
TEMA 0: CONCEPTOS BÁSICOS.
 TEMA : CONCEPTOS BÁSICOS.. Intervlos:. Intervlos. 2. Propieddes de ls potencis.. Propieddes de los rdicles. Operciones con rdicles. Rcionlizción. 4. Conceptos de un polinomio. Fctorizción de polinomios..
TEMA : CONCEPTOS BÁSICOS.. Intervlos:. Intervlos. 2. Propieddes de ls potencis.. Propieddes de los rdicles. Operciones con rdicles. Rcionlizción. 4. Conceptos de un polinomio. Fctorizción de polinomios..
Números y operaciones
 1 Números y operaciones Rosa y Julián tienen en su granja ciento veinte vacas, ochenta de leche y el resto de engorde. Además, crían tres cerdos, cuatro pavos y el triple de gallinas que de pavos. También,
1 Números y operaciones Rosa y Julián tienen en su granja ciento veinte vacas, ochenta de leche y el resto de engorde. Además, crían tres cerdos, cuatro pavos y el triple de gallinas que de pavos. También,
HOJA 5 SUCESIONES Y PROGRESIONES
 HOJA 5 SUCESIONES Y PROGRESIONES Sucesión: Término general 1.- Calcula el término general de las sucesiones: a) -1, 2, 5, 8, 11, b) 3, 3/2, ¾, 3/8, c) 1, 4, 9, 16, 25, 2.- Halla el término general de cada
HOJA 5 SUCESIONES Y PROGRESIONES Sucesión: Término general 1.- Calcula el término general de las sucesiones: a) -1, 2, 5, 8, 11, b) 3, 3/2, ¾, 3/8, c) 1, 4, 9, 16, 25, 2.- Halla el término general de cada
Ordena estos ordinales de mayor a menor y escribe su nombre:
 Ordena estos ordinales de mayor a menor y escribe su nombre: 2º - 7º- 5º - 10º - 1º - 3º - 6º - 4º - 9º - 8º. 1º 2º.. 3º. 4º 5º.. 6º.. 7º. 8º.. 9º 10º Descomponer estos números en sumas. Pon su nombre.
Ordena estos ordinales de mayor a menor y escribe su nombre: 2º - 7º- 5º - 10º - 1º - 3º - 6º - 4º - 9º - 8º. 1º 2º.. 3º. 4º 5º.. 6º.. 7º. 8º.. 9º 10º Descomponer estos números en sumas. Pon su nombre.
Números. Subclases dentro de los reales. Lectura sugerida
 Lectur sugerid Selección 1: Subclses dentro de los reles. Nturles. Enteros. Rcionles. Irrcionles. Operciones. Un comentrio y vris clrciones. Vlor bsoluto y signo. Enteros. Sum de enteros. Producto de enteros.
Lectur sugerid Selección 1: Subclses dentro de los reles. Nturles. Enteros. Rcionles. Irrcionles. Operciones. Un comentrio y vris clrciones. Vlor bsoluto y signo. Enteros. Sum de enteros. Producto de enteros.
1.. VALOR POSICIONAL DE CADA CIFRA EN UN NÚMERO DECIMAL.
 1.. VALOR POSICIONAL DE CADA CIFRA EN UN NÚMERO DECIMAL. Un número decimal tiene dos partes: una parte entera, a la izquierda de la coma y una parte decimal a la derecha de la coma. Lectura y escritura.
1.. VALOR POSICIONAL DE CADA CIFRA EN UN NÚMERO DECIMAL. Un número decimal tiene dos partes: una parte entera, a la izquierda de la coma y una parte decimal a la derecha de la coma. Lectura y escritura.
Resolución de circuitos complejos de corriente continua: Leyes de Kirchhoff.
 Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
EJERCICIOS PROPUESTOS. a) 9 500 b) 3 c) 2 d) 20 e) 25
 2 NÚMEROS ENTEROS EJERCICIOS PROPUESTOS 2.1 Expresa con un número entero las siguientes informaciones. a) El avión está volando a 9 500 metros de altura. b) La temperatura mínima de ayer fue de 3 C bajo
2 NÚMEROS ENTEROS EJERCICIOS PROPUESTOS 2.1 Expresa con un número entero las siguientes informaciones. a) El avión está volando a 9 500 metros de altura. b) La temperatura mínima de ayer fue de 3 C bajo
PENDIENTE MATEMÁTICAS DE 2º ESO CUADERNILLO I
 PENDIENTE MATEMÁTICAS DE º ESO CUADERNILLO I Fech de entreg de enero Fech del primer emen de enero NOMBRE CURSO Bloques temáticos Criterios de evlución Ejercicios.- Números enteros. I, II Del l.- Sistem
PENDIENTE MATEMÁTICAS DE º ESO CUADERNILLO I Fech de entreg de enero Fech del primer emen de enero NOMBRE CURSO Bloques temáticos Criterios de evlución Ejercicios.- Números enteros. I, II Del l.- Sistem
LOS CONJUNTOS NUMÉRICOS
 Pontifici Universidd Ctólic de Chile Fcultd de Educción Nivelción de Estudios pr Adultos CREA Educción Mtemátic Nivel 2 Profesor Jun Núñez Fernández LOS CONJUNTOS NUMÉRICOS Como se mencionó en l clse nterior,
Pontifici Universidd Ctólic de Chile Fcultd de Educción Nivelción de Estudios pr Adultos CREA Educción Mtemátic Nivel 2 Profesor Jun Núñez Fernández LOS CONJUNTOS NUMÉRICOS Como se mencionó en l clse nterior,
2. REPRESENTACIÓN ANALÍTICA Y GRÁFICA DE UN VECTOR
 1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid
1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid
Colegio Diocesano Sagrado Corazón de Jesús EJERCICIOS MATEMÁTICAS 3º ESO VERANO 2015
 Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS
 UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS Unidad 6: Polinomios con coeficientes enteros. Al final deberás haber aprendido... Expresar algebraicamente enunciados sencillos. Extraer enunciados razonables
UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS Unidad 6: Polinomios con coeficientes enteros. Al final deberás haber aprendido... Expresar algebraicamente enunciados sencillos. Extraer enunciados razonables
DESIGUALDADES < d < En el campo de los números reales tenemos una. Un momento de reflexión muestra que una
 DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
RECUPERACIÓN DE MATEMÁTICAS 1ª EVALUACIÓN. 4º DE ESO
 RECUPERACIÓN DE MATEMÁTICAS ª EVALUACIÓN. 4º DE ESO TEMA ª.- Nos dicen que l medid de un cmpo de form rectngulr es de 4,6 m de lrgo por 8,4 m de ncho. Sin embrgo, no estmos seguros de que ls cifrs decimles
RECUPERACIÓN DE MATEMÁTICAS ª EVALUACIÓN. 4º DE ESO TEMA ª.- Nos dicen que l medid de un cmpo de form rectngulr es de 4,6 m de lrgo por 8,4 m de ncho. Sin embrgo, no estmos seguros de que ls cifrs decimles
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS
 TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
2Unidad. Expresiones algebraicas. fraccionarias EN ESTA UNIDAD APRENDERÁS A: 68 Unidad 2
 Epresiones lgebrics Unidd frccionris EN ESTA UNIDAD APRENDERÁS A: Interpretr ls epresiones lgebrics frccionris como un generlizción de l opertori con frcciones numérics. Reconocer pr qué vlores un epresión
Epresiones lgebrics Unidd frccionris EN ESTA UNIDAD APRENDERÁS A: Interpretr ls epresiones lgebrics frccionris como un generlizción de l opertori con frcciones numérics. Reconocer pr qué vlores un epresión
Lección 24: Lenguaje algebraico y sustituciones
 LECCIÓN Lección : Lenguaje algebraico y sustituciones En lecciones anteriores usted ya trabajó con ecuaciones. Las ecuaciones expresan una igualdad entre ciertas relaciones numéricas en las que se desconoce
LECCIÓN Lección : Lenguaje algebraico y sustituciones En lecciones anteriores usted ya trabajó con ecuaciones. Las ecuaciones expresan una igualdad entre ciertas relaciones numéricas en las que se desconoce
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 9 EJERCICIOS Ls relciones de proporcionlidd 1 Indic, entre los siguientes pres de mgnitudes, los que son directmente proporcionles, los que son inversmente proporcionles y los que no gurdn
Pág. 1 PÁGINA 9 EJERCICIOS Ls relciones de proporcionlidd 1 Indic, entre los siguientes pres de mgnitudes, los que son directmente proporcionles, los que son inversmente proporcionles y los que no gurdn
PROPORCIONALIDAD - teoría
 PROPORCIONALIDAD RAZÓN: razón de dos números es el cociente indicado de ambos. Es decir, la razón de los dos números a y b es a:b, o lo que es lo mismo, la fracción b a. PROPORCIÓN: es la igualdad de dos
PROPORCIONALIDAD RAZÓN: razón de dos números es el cociente indicado de ambos. Es decir, la razón de los dos números a y b es a:b, o lo que es lo mismo, la fracción b a. PROPORCIÓN: es la igualdad de dos
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
OPERACIONES CON FRACIONES
 LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
Nombre: 40 X 5= 55+ 22= Escribe en letras los siguientes números 81.424 37.609 49.005 24.098 56.704 64.322
 Escribe en letras los siguientes números 81.424 37.609 49.005 24.098 56.704 64.322 Escribe todos los números de 4 cifras que tienen 3 millares, 5 decenas y 9 unidades 40 X 5= 55+ 22= Observa los precios
Escribe en letras los siguientes números 81.424 37.609 49.005 24.098 56.704 64.322 Escribe todos los números de 4 cifras que tienen 3 millares, 5 decenas y 9 unidades 40 X 5= 55+ 22= Observa los precios
1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20
 ACTIVIDADES DE REPASO MATEMÁTICAS 1º ESO NOMBRE: GRUPO:. Actividades a realizar: 1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20 2) Calcula: a) 4 6 + 3 + 9-2 3 = b) 6 (3 + 7) -
ACTIVIDADES DE REPASO MATEMÁTICAS 1º ESO NOMBRE: GRUPO:. Actividades a realizar: 1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20 2) Calcula: a) 4 6 + 3 + 9-2 3 = b) 6 (3 + 7) -
- 1 - PLANO INCLINADO
 - 1 - PLNO INCLINDO DESCOMPOSICIÓN DE L FUERZ PESO Suponé que tengo un cuerpo que está poydo en un plno que está inclindo un ángulo. L fuerz peso punt pr bjo de est ner: UN CUERPO POYDO EN UN PLNO INCLINDO.
- 1 - PLNO INCLINDO DESCOMPOSICIÓN DE L FUERZ PESO Suponé que tengo un cuerpo que está poydo en un plno que está inclindo un ángulo. L fuerz peso punt pr bjo de est ner: UN CUERPO POYDO EN UN PLNO INCLINDO.
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
DETERMINANTES. Determinante es la expresión numérica de una matriz. Según el orden de la matriz el determinante se resuelve de distintas formas:
 ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
73 ESO. E = m c 2. «El que pregunta lo que no sabe es ignorante un. día. El que no lo pregunta será ignorante toda la vida»
 73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
INTEGRACIÓN. CÁLCULO DE
 Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
UNIDAD N 3: EXPRESIONES ALGEBRAICAS POLINOMIOS
 Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Regla de Sarrus: Para recordar con mayor facilidad el desarrollo del determinante de orden 3, podemos usar esta regla:
 UNIDD 8: Determinntes. DETERMINNTES DE ORDEN Y Definición: Pr un mtriz cudrd de orden, por det( ) ó, l siguiente nº rel: det( ) = = = Definición: Pr un mtriz cudrd de orden, not por det( ) ó, l siguiente
UNIDD 8: Determinntes. DETERMINNTES DE ORDEN Y Definición: Pr un mtriz cudrd de orden, por det( ) ó, l siguiente nº rel: det( ) = = = Definición: Pr un mtriz cudrd de orden, not por det( ) ó, l siguiente
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
