LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Límite de una función en un punto
|
|
|
- Cristóbal Murillo Contreras
- hace 7 años
- Vistas:
Transcripción
1 LÍMITES, CONTINUIDAD, ASÍNTOTAS. LÍMITE DE UNA FUNCIÓN.. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límit d una función n un punto f ) = l S l: El it cuando tind a c d f) s l c Significa: l s l valor al qu s aproima f) cuando s aproima a c Notas: - Qu s aproima a c gnifica qu toma valors muy crca d c S pud acrcar por la izquirda o por la drch. - l pud sr + ó - y ntoncs = c s una asíntota vrtical. Límits latrals d una función n un punto Límit por la drcha: f ) = l S l: El it cuando tind a c por la drcha d f) s l c + Significa: l s l valor al qu s aproima f) cuando s aproima a c por la drcha. Límit por la izquirda: f ) = l S l: El it cuando tind a c por la izquirda d f) s l c Significa: l s l valor al qu s aproima f) cuando s aproima a c por la izquirda. Eistn dl it Para qu ista l it d una función n un punto s ncsario qu istan los dos its latrals y san iguals.
2 .. LÍMITES EN EL INFINITO f ) + f ) + = + = S l: El it cuando tind a más infinito d f) s más infinito Significa: la función toma valors grands potivos cuando la toma valors grands potivos. º cuadrant) S l: El it cuando tind a más infinito d f) s mnos infinito. Significa: la función toma valors grands ngativos cuando la toma valors grands potivos. º cuadrant) f ) = l S l: El it cuando tind a más infinito d f) s l + Significa: l s l valor al qu s aproima f) cuando toma valors muy grands potivos: y = l s una asíntota vrtical. f ) f ) = + = S l: El it cuando tind a mnos infinito d f) s más infinito Significa: la función toma valors grands potivos cuando la toma valors grands ngativos. º cuadrant) S l: El it cuando tind a mnos infinito d f) s mnos infinito. Significa: la función toma valors grands ngativos cuando la toma valors grands ngativos. º cuadrant) f ) = l S l: El it cuando tind a mnos infinito d f) s l Significa: l s l valor al qu s aproima f) cuando toma valors muy grands ngativos: y = l s una asíntota vrtical.
3 .. CÁLCULO DE LÍMITES S sustituy la por l valor al qu tind b) d) sn + ) ) log π g) j) + + m) Indtrminacions:, h) + 7 c) 7 f) i) k) + l) + n) ñ) + k Hallar its latrals b) d) ) Factorizar y mplificar + + b) ) c) c) f) ) ± a b Si grado dl numrador > grado dl dnominado r El gno dpnd coficint s + + c) Si grado dl numrador d la d mayor grado dl numrador y dl dnominado r) = grado dl dnominado r a y b son los coficint s d la d mayor grado dl numrador y dl dnominado r) Si grado dl numrador < grado dl dnominado r b) + + d) - S hacn opracions. Cuando aparcn radicals, multiplicamos y dividimos por la prón conjugada. b) + d los
4 f ) : Tipo númro : Aplicar : = a + f) f ) a g) = ó g).[f ) ] a - En funcions dfinidas a trozos, n los puntos dond sté dfinida d distinta forma m aproimo por valors más pquños, qu por valors más grands, habrá qu hacr its latrals. Dada la función f) = <. ASÍNTOTAS Y RAMAS INFINITAS - Asíntotas vrticals: = c y Cálculo: Puntos qu anulan l dnominador Puntos qu anulan lo qu stá dntro dl logaritmo Por abajo Aproimación: Calcular los its latrals + Por arriba Calcular su it n los puntos,, 7 - Asíntotas horizontals: y = b Grado numrador Grado dnominador) Cálculo: f ) = b Aproimación: f± ) Asíntota < > Por dbajo Por ncima - Asíntotas oblicuas: y = m + n Grado Numrador Grado dnominador = ) Cálculo: m = f ) Aproimación: f± ) Asíntota± ) ; n = f ) m) < > Por dbajo Por ncima RAMAS INFINITAS Grado Numrador Grado dnominador ) Cálculo: f ) = ± ± y = d) y = b) y = ) y = + + c) y = f) y = + +
5 . - CONTINUIDAD La ida d función continua s la d qu pud sr construida con un solo trazo. Una función f) s continua n l punto = a f) f a = Todas las funcions dfinidas por prons analíticas lmntals s dcir, todas las qu conocmos hasta ahora, cptuando las funcions a trozos), son continuas n todos los puntos d su dominio. Las funcions a trozos habrá qu studiarlas n los trmos d sus trozos qu prtnzcan al dominio. Tipos d discontinuidads - Discontinua invitabl d salto infinito: Si alguno d los its latrals s infinito o no ist. - Discontinua invitabl d salto finito: Si los dos its latrals son finitos pro distintos. El salto s la difrncia, n valor absoluto, d los its latrals. - Discontinua vitabl: Si los dos its latrals son finitos iguals, pro su valor no coincid con f o no ist f y = + b) y = c) y = d) log < ) y = + f) y = g) y = + = + h) Calcular l valor d n para qu la función f) = sa + n > continua n todo R. + k i) Calcular k para qu y = sa continua n R 7 =
6 CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : Y X f b) f c) f d) f ) f f b) f c) f d) f ) f EJERCICIO : A partir d la gráfica d f), calcula: 8 Y 8 8 X f b) f c) d) f f ) f f b) f c) f d) f ) f EJERCICIO : Rprsnta gráficamnt los guints rsultados: b) f b) g EJERCICIO : Rprsnta los guints its: f f EJERCICIO : Rprsnta n cada caso los guints rsultados: f b) g b) o bin
7 EJERCICIO : Rprsnta gráficamnt: f b) g b) Por jmplo: o bin Rprsnta gráficamnt stos dos its. EJERCICIO 7 : Para la función f, sabmos qu : y CÁLCULO DE LÍMITES INMEDIATOS EJERCICIO 8 : Calcula los guints its: b) 9 c) cos d) ) b) c) cos cos d) ) 7 9 EJERCICIO 9 : Calcula l it d la función f n y n. 7 EJERCICIO : Calcula los guints its y rprsnta los rsultados qu obtngas: b) c) b) c) Hallmos los its latrals: ;
8 EJERCICIO : Rsulv los guints its y rprsnta gráficamnt los rsultados obtnidos: b) c) b) 8 c) 8 Hallamos los its latrals: ; EJERCICIO : Halla los its guints y rprsnta gráficamnt la información qu obtngas: b) c) 9 b) c) Hallamos los its latrals: ; EJERCICIO : Halla los guints its y rprsnta los rsultados qu obtngas: b) c) 7 9 b) c) Hallamos los its latrals: ; EJERCICIO : Calcula los its guints y rprsnta gráficamnt los rsultados qu obtngas: b) c)
9 b) c) Hallamos los its latrals: ; CÁLCULO DE LÍMITES EJERCICIO : Calcula los guints its y rprsnta los rsultados qu obtngas: b) c) d) ) f) g) h) i) j) k) b) c) d) Hallamos los its latrals: ) f) g) h)
10 i) j) k) EJERCICIO : Halla l it cuando d las guints funcions y rprsnta gráficamnt la información qu obtngas: f b) f b) EJERCICIO 7 : Calcula l it cuando y rprsnta la información qu obtngas: f y cuando dla guint función EJERCICIO 8 : Halla los guints its y rprsnta gráficamnt los rsultados obtnidos: b) b) EJERCICIO 9 : Calcula los guints its y rprsnta l rsultado qu obtngas: b) b)
11 CÁLCULO DE LÍMITES EJERCICIO : Calcula: b) log ) f) log i) log j) c) 9 d) g) ln h) Porqu una ponncial d bas mayor qu s un infinito d ordn suprior a una potncia. b) log log Porqu una potncia s un infinito d ordn suprior a un logaritmo. 9 9 c) d) ) log Porqu las potncias son infinitos d ordn suprior a los logaritmos. f) g) Porqu una ponncial d bas mayor qu s un infinito d ordn suprior a una potncia. ln ln h) Porqu las potncias son infinitos d ordn suprior a los logaritmos. i) log Porqu las potncias son infinitos d ordn suprior a los logaritmos. j) EJERCICIO : Halla los its: b) c) ) f) g) i) j) d) h)
12 7 9 b) c) ) ) ) ) ) d) ) f) g) h) ) ) ) ) i) j) EJERCICIO : Calcula: 7 8 b) c) d) 9 ) 7 8 b) ) ) ) ) ) ) ) ) ) )
13 8 ) ) ) c) ) Hallamos los its latrals: ; No ist d) 9 ) 8 Hallamos los its latrals: ; No ist ) ) 9 Hallamos los its latrals: ; No ist EJERCICIO : Calcula los its: b) c) d) ) ) ) ) ) ) ) ) ) ) b) ) ) ) ) ) ) ) ) ) c) 8 d) )
14 9 EJERCICIO : Calcula stos its: b) c) d) ) f) g) 9 7 h) i) j) b) 8 c) d) ) f) g) h) i) j) EJERCICIO : Halla los its: 9 b) c) d) ) f) g) h) i) j)
15 ) ) ) ) ) 9 b) Hallamos los its latrals: ) ) ; ) ) Como son distintos No ist l it ) ) c) Hallamos los its latrals: ; Como son distintos No ist l it d) ) f) ) Hallamos los its latrals: ; No ist l it ) ) ) ) g). h) i) ) ) j)
16 CONTINUIDAD EJERCICIO : La guint gráfica corrspond a la función f : Y X Di s continua o no n y n. Si n alguno d los puntos no s continua, indica cuál s la causa d la discontinuidad. En no s continua porqu prsnta un salto n s punto. Obsrvamos qu f f En sí s continua. EJERCICIO 7 : A partir d la gráfica d f ) sñala s continua o no n y n. En l caso d no sr continua, indica la causa d la discontinuidad.. Y X En =, sí s continua. En = s discontinua porqu no stá dfinida, ni tin it finito. Tin una rama infinita n s punto una asíntota vrtical). EJERCICIO 8 : Dada la gráfica d f : Y X Es continua n? b) Y n? Si no s continua n alguno d los puntos, indica cuál s la razón d la discontinuidad. Sí s continua n. b) No, n s discontinua porqu no stá dfinida n s punto. Como sí tin it n s punto, s una discontinuidad vitabl. EJERCICIO 9 : Avrigua la guint función s continua n : f f f Es continua n porqu f f. f
17 EJERCICIO : Compruba la guint función s continua n. f f Es continua n f porqu f f. EJERCICIO : Halla l valor d k para qu f sa continua n : f f f. En : f k k = f ). f continua n = k = f k EJERCICIO : Estudia la continuidad d las guints funcions y rprséntalas gráficamnt: f b) f c) f d) f ) f f) f g) f h) f i) f j) f Continuidad: f continua n R {} f f. En : f f discontinua invitabl d salto finito) n = f ) Rprsntación: f Si, s un trozod parábola. V = ) Si, s un trozo d rcta. X Y Y X
18 b) Continuidad f continua n R {} f f. En : f f continua n = f ). f continua n todo R. Rprsntación Si, s un trozod parábola. V = ) Si, s un trozo d rcta. Y 8 X Y X c) Continuidad f continua n R {-} f f. En -: f f continua n = - f ) f continua n todo R. Rprsntación: Si, s un trozod rcta. Si, s un trozo d parábola. V = ) Y X Y X d) Continuidad f continua n R {} f f. En : f f continua n = f ) f continua n todo R Rprsntación: Si, s un trozod rcta horizontal. Si, s un trozo d parábola. V = ) Y X Y - - X
19 ) Continuidad: f continua n R {} f f. En : f f discontinua invitabl d salto finito) n = f ) Rprsntación: Y Si, s un trozod parábola. V = ) 8 Si, s un trozo d rcta. f) Continuidad: f continua n R {} f f. En : f f continua n = f ) f continua n todo R. Rprsntación: Si, s un trozo d parábola. V = ) Si >, s un trozo d rcta horizontal. X Y X g) Continuidad f continua n R {} f f. En : f f continua n = f ) f continua n todo R. Rprsntación: Si, s un trozo d parábola. V = ) Si >, s un trozo d rcta. X Y + / + h) Continuidad f continua n R {} f f. En : f f discontinua invitabl d salto finito) n = f )
20 Rprsntación: Si, s un trozo d parábola.v = ) Si >, s un trozo d rcta horizontal. X Y - - i) Continuidad f continua n R {-} f f. En -: f f discontinua invitabl d salto finito) n f ). ) =- Rprsntación Si s un trozo d rcta. Si > s un trozo d parábola. V = ) X Y j) Continuidad f continua n R {} f f. En : f f continua n = f ) f continua n todo R Rprsntación: Si, s un trozo d parábola.v = ) Si >, s un trozo d rcta. X Y ASÍNTOTAS EJERCICIO : Calcula l it d la guint función n l punto y studia su comportaminto por la izquirda y por la drcha: f Calculamos los its latrals:
21 EJERCICIO : Calcula l guint it y studia l comportaminto d la función a la izquirda y a la drcha d : 9 9 Calculamos los its latrals: 9 9 EJERCICIO : Calcula l guint it y studia l comportaminto d la función por la izquirda y por la drcha d : Calculamos los its latrals: EJERCICIO : Calcula l guint it y studia l comportaminto d la función por la izquirda y por la drcha d : EJERCICIO 7 : Dada la función f la información qu obtngas., calcula l it d f ) n. Rprsnta Calculamos los its latrals: EJERCICIO 8 : Halla las asíntotas vrticals d las guints funcions y túa las curvas rspcto a llas: f b) f ;. Las asíntotas vrticals son y. Poción d la curva rspcto a llas:
22 7 b) Solo tin una asíntota vrtical: Poción d la curva rspcto a la asíntota: EJERCICIO 9 : Halla las ramas infinitas d las guints funcions y rprsnta los rsultados obtnidos: f b) f c) f d) f b) c) d) EJERCICIO : Halla las ramas infinitas, cuando, d las guints funcions la información qu obtngas: f b) f y rprsnta b) EJERCICIO : Halla las ramas infinitas, cuando, d las guints funcions y rprsnta los rsultados qu obtngas: f b) f b)
23 8 EJERCICIO : Calcular las asíntotas horizontals d stas funcions y rprsnta los rsultados qu obtngas: f b) f f ) A.V.y f ) b) f ) A.V.y f ) EJERCICIO : Las guints funcions tinn una asíntota oblicua. Hállala y túa las curvas rspcto a llas: f b) f y = m + n f ) m y n f ) m. Asíntota oblicua : f ) A n t) y f ) A n t ) y= + b) f ) m n f ) m. y Asíntota oblicua: y f ) A n t) f ) A n t ) y=
24 EJERCICIO : Halla las asíntotas d las guints funcions y túa las curvas rspcto a llas: f b) f Asíntotas vrticals: Puntos qu anulan l dnominador: = = ; ; = = Asíntota horizontal: Rprsntación: f ) y = f ) 9 b) Asíntota vrtical: Puntos qu anulan l dnominador = f ) Asíntota horizontal: y = f ) Rprsntación:
25 LÍMITES Cálculo y rprsntación ) ASÍNTOTAS Y RAMAS INFINITAS Cálculo y rprsntación. y = - +. y = + +. y = + +. y = + +. y =
26
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS
 Tma Límits, continuidad y asíntotas Matmáticas I º Bachillrato TEMA LÍMITES, CONTINUIDAD ASÍNTOTAS CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : 8 8 8 f f c) f f ) f f f c) f f )
Tma Límits, continuidad y asíntotas Matmáticas I º Bachillrato TEMA LÍMITES, CONTINUIDAD ASÍNTOTAS CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : 8 8 8 f f c) f f ) f f f c) f f )
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8. LÍMITE DE UNA FUNCIÓN 8.. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límit d una función n un punto f () = l S l: El it cuando tind a c d f() s l c Significa:
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8. LÍMITE DE UNA FUNCIÓN 8.. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límit d una función n un punto f () = l S l: El it cuando tind a c d f() s l c Significa:
ASÍNTOTAS Y RAMAS INFINITAS Cálculo y representación
 LÍMITES Cálculo y rprsntación...... 7. 8. - + + - - + + - + - ( + ) - + + - - + + 9. + - +. + - + - 9. + -. + + + - +. + + +. + + + -. +. + - ASÍNTOTAS Y RAMAS INFINITAS Cálculo y rprsntación. y = - +.
LÍMITES Cálculo y rprsntación...... 7. 8. - + + - - + + - + - ( + ) - + + - - + + 9. + - +. + - + - 9. + -. + + + - +. + + +. + + + -. +. + - ASÍNTOTAS Y RAMAS INFINITAS Cálculo y rprsntación. y = - +.
LÍMITES DE FUNCIONES. CONTINUDAD
 LÍMITES DE FUNCIONES. CONTINUDAD Signiicado dl it Ejrcicio nº.- Rprsnta gráicamnt y plica l gniicado d la prón: Ejrcicio nº.- Eplica l gniicado d la guint prón y rprséntalo gráicamnt: 9 Ejrcicio nº.- Escrib
LÍMITES DE FUNCIONES. CONTINUDAD Signiicado dl it Ejrcicio nº.- Rprsnta gráicamnt y plica l gniicado d la prón: Ejrcicio nº.- Eplica l gniicado d la guint prón y rprséntalo gráicamnt: 9 Ejrcicio nº.- Escrib
LÍMITES DE FUNCIONES.
 LÍMITES DE FUNCIONES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Sa y una unción ral d variabl ral. D una manra intuitiva y oco rcisa, dirmos qu l it d s L, cuando s aroima a, si ocurr qu cuanto más róimo sté
LÍMITES DE FUNCIONES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Sa y una unción ral d variabl ral. D una manra intuitiva y oco rcisa, dirmos qu l it d s L, cuando s aroima a, si ocurr qu cuanto más róimo sté
EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL
 EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
REPRESENTACION GRAFICA.
 REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
2º Bachillerato: ejercicios modelo para el examen de las lecciones 11, 12 y 13
 º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
RESUMEN DE FUNCIONES. LIMITE Y CONTINUIDAD
 RESUMEN DE FUNCIONES. LIMITE Y CONTINUIDAD DEFINICIÓN DE FUNCIÓN REAL DE VARIABLE REAL Una unción ral d variabl ral s una aplicación d un subconjunto D d los númros rals n un subconjunto I d los númros
RESUMEN DE FUNCIONES. LIMITE Y CONTINUIDAD DEFINICIÓN DE FUNCIÓN REAL DE VARIABLE REAL Una unción ral d variabl ral s una aplicación d un subconjunto D d los númros rals n un subconjunto I d los númros
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
REPRESENTACIÓN DE FUNCIONES
 Matmáticas º Bachillrato. Prosora: María José Sánchz Quvdo REPRESENTACIÓN DE FUNCIONES Para l studio y rprsntación d una unción s sigun los siguints pasos:. Dominio d dinición y d continuidad.. Corts con
Matmáticas º Bachillrato. Prosora: María José Sánchz Quvdo REPRESENTACIÓN DE FUNCIONES Para l studio y rprsntación d una unción s sigun los siguints pasos:. Dominio d dinición y d continuidad.. Corts con
PROBLEMAS RESUELTOS DE RECTAS TANGENTES Y NORMALES
 PROBLEMAS RESUELTOS DE RECTAS TANGENTES Y NORMALES ) (Part d un problma d Slctividad d Cincias y Tcnología 007) Sa f: R R la función dfinida por f() =. Dtrmina la cuación d la rcta tangnt a la gráfica
PROBLEMAS RESUELTOS DE RECTAS TANGENTES Y NORMALES ) (Part d un problma d Slctividad d Cincias y Tcnología 007) Sa f: R R la función dfinida por f() =. Dtrmina la cuación d la rcta tangnt a la gráfica
I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN PARCIAL. PRIMERA EVALUACIÓN. ANÁLISIS
 Eamn Parcial. Análisis. Matmáticas II. Curso 010-011 I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN PARCIAL. PRIMERA EVALUACIÓN. ANÁLISIS Curso 010-011 19-XI-010 MATERIA: MATEMÁTICAS II INSTRUCCIONES
Eamn Parcial. Análisis. Matmáticas II. Curso 010-011 I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN PARCIAL. PRIMERA EVALUACIÓN. ANÁLISIS Curso 010-011 19-XI-010 MATERIA: MATEMÁTICAS II INSTRUCCIONES
12 Representación de funciones
 Rprsntación d funcions ACTIVIDADES INICIALES.I. Factorizando prviamnt las prsions, rsulv las siguints cuacions: a) 6 7 5 0 6 c) 0 7 b) 6 d) 0 a) 6 7 5 0 ( )(6 5) 0 5 6 5 0, b) 7 6 ( )( ) 6 6 ( ) 7 ( )
Rprsntación d funcions ACTIVIDADES INICIALES.I. Factorizando prviamnt las prsions, rsulv las siguints cuacions: a) 6 7 5 0 6 c) 0 7 b) 6 d) 0 a) 6 7 5 0 ( )(6 5) 0 5 6 5 0, b) 7 6 ( )( ) 6 6 ( ) 7 ( )
Matemáticas II TEMA 8 Derivadas. Teorema. Regla de L Hôpital Problemas Propuestos
 Matmáticas II TEMA 8 Drivadas Torma Rgla d L Hôpital Problmas Propustos Drivada d una función n un punto Utilizando la dfinición, calcula la drivada d f ( ) n l punto = Utilizando la dfinición, halla la
Matmáticas II TEMA 8 Drivadas Torma Rgla d L Hôpital Problmas Propustos Drivada d una función n un punto Utilizando la dfinición, calcula la drivada d f ( ) n l punto = Utilizando la dfinición, halla la
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES.
 TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bach. TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. Tasa d variación mdia. Cálculo y signiicado EJERCICIO : Considramos la unción:. Halla la tasa
TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bach. TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. Tasa d variación mdia. Cálculo y signiicado EJERCICIO : Considramos la unción:. Halla la tasa
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1
 TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1 TEMA 11 LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN 11.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función en un
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1 TEMA 11 LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN 11.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función en un
Soluciones a los ejercicios propuestos Unidad 1. El conjunto de los números reales Matemáticas aplicadas a las Ciencias Sociales I
 Solucions a los jrcicios propustos Unidad. El conjunto d los númros rals Matmáticas aplicadas a las Cincias Socials I NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES. Dtrmina si los siguints númros son o no
Solucions a los jrcicios propustos Unidad. El conjunto d los númros rals Matmáticas aplicadas a las Cincias Socials I NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES. Dtrmina si los siguints númros son o no
Convocatoria de Febrero 26 de Enero de 2007. Nombre y Apellidos:
 Univrsidad d Vigo Dpartamnto d Matmática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria d Fbrro 6 d Enro d 007 Nombr y Apllidos: DNI: (4.5 p.) ) S considra la función f(x) = x ln(x). (0.5 p.) (a) Calcular
Univrsidad d Vigo Dpartamnto d Matmática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria d Fbrro 6 d Enro d 007 Nombr y Apllidos: DNI: (4.5 p.) ) S considra la función f(x) = x ln(x). (0.5 p.) (a) Calcular
Para que exista límite de una f(x) en un punto han de coincidir los límites laterales en dicho punto.
 REPASO LÍMITES º BACH. RECORDAR: Para qu ista límit d una f() n un punto han d coincidir los límits latrals n dicho punto. A fctos dl f() no tnmos n cunta lo qu ocurr actamnt n a, sino n las a proimidads.
REPASO LÍMITES º BACH. RECORDAR: Para qu ista límit d una f() n un punto han d coincidir los límits latrals n dicho punto. A fctos dl f() no tnmos n cunta lo qu ocurr actamnt n a, sino n las a proimidads.
ANÁLISIS. Junio 94. cosx si x Dada la función. f(x) a 2x si 0 x 1. b si x 1 x
 ANÁLISIS Junio 9.. Dada la función cos si 0 b si f() a si 0 a) [ punto] Calcular los valors d a y b para qu la función f() sa continua n b) [ punto] Es drivabl la función obtnida n = 0?. En =?. Razona
ANÁLISIS Junio 9.. Dada la función cos si 0 b si f() a si 0 a) [ punto] Calcular los valors d a y b para qu la función f() sa continua n b) [ punto] Es drivabl la función obtnida n = 0?. En =?. Razona
Matemáticas II (Bachillerato de Ciencias). Soluciones de los problemas propuestos. Tema 8
 Matmáticas II (Bacillrato d Cincias) Solucions d los problmas propustos Tma 8 7 TEMA 8 Drivadas Tormas Rgla d L Hôpital Problmas Rsultos Drivada d una función n un punto Utilizando la dfinición, calcula
Matmáticas II (Bacillrato d Cincias) Solucions d los problmas propustos Tma 8 7 TEMA 8 Drivadas Tormas Rgla d L Hôpital Problmas Rsultos Drivada d una función n un punto Utilizando la dfinición, calcula
Tema 8 Límites Matemáticas II 2º Bachillerato 1. EJERCICIO 1 : Da una definición para estas expresiones y represéntalas gráficamente: c) 2.
 Tm Límits Mtmátics II º Bchillrto TEMA LIMITES CÁLCULO DE LÍMITES EJERCICIO : D un dinición pr sts prons y rprséntls gráicmnt: ) ) 9 6 c) ) ) Cundo s proim, l unción s hc muy grnd ) Cundo s proim, l unción
Tm Límits Mtmátics II º Bchillrto TEMA LIMITES CÁLCULO DE LÍMITES EJERCICIO : D un dinición pr sts prons y rprséntls gráicmnt: ) ) 9 6 c) ) ) Cundo s proim, l unción s hc muy grnd ) Cundo s proim, l unción
ANÁLISIS. a) Derivabilidad de la función en los puntos x = -1, x = 1, x = 2. Calcular la derivada en cada uno de los puntos
 Matmáticas II Prubas d Accso a la Univrsidad ANÁLISIS Junio 9.. Dada la función cos f () a b si si si a) Calcular los valors d a y b para qu la función f() sa continua n [ punto] b) Es drivabl la función
Matmáticas II Prubas d Accso a la Univrsidad ANÁLISIS Junio 9.. Dada la función cos f () a b si si si a) Calcular los valors d a y b para qu la función f() sa continua n [ punto] b) Es drivabl la función
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
 III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
Tema 2 La oferta, la demanda y el mercado
 Ejrcicios rsultos d ntroducción a la Toría Económica Carmn olors Álvarz Alblo Migul Bcrra omínguz Rosa María Cácrs Alvarado María dl Pilar Osorno dl Rosal Olga María Rodríguz Rodríguz Tma 2 La ofrta, la
Ejrcicios rsultos d ntroducción a la Toría Económica Carmn olors Álvarz Alblo Migul Bcrra omínguz Rosa María Cácrs Alvarado María dl Pilar Osorno dl Rosal Olga María Rodríguz Rodríguz Tma 2 La ofrta, la
Aproximación intuitiva al concepto de límite de una función en un punto
 Aproimación intuitiva al concepto de límite de una función en un punto ) Consideremos el siguiente gráfico Cuando los valores de se aproiman a 8 por la derecha, las imágenes de se acercan a 4 Cuando los
Aproimación intuitiva al concepto de límite de una función en un punto ) Consideremos el siguiente gráfico Cuando los valores de se aproiman a 8 por la derecha, las imágenes de se acercan a 4 Cuando los
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas y x 12x 2 y log 2 x ln x e e y ln 1 x
 . Drivar las siguints funcions simplificar l rsultado n la mdida d lo posibl. ) 4) 7) ) 4 5 5 5 7 5) 8) ) 5 6) 5 9) 4 5 0) ) 7 ) ) 4) 4 5) 6) 7) 8) 9) ) 5) 0) 4 ln ) ln log 6) ln 8) ln ) 9) ) 5) 4) 7)
. Drivar las siguints funcions simplificar l rsultado n la mdida d lo posibl. ) 4) 7) ) 4 5 5 5 7 5) 8) ) 5 6) 5 9) 4 5 0) ) 7 ) ) 4) 4 5) 6) 7) 8) 9) ) 5) 0) 4 ln ) ln log 6) ln 8) ln ) 9) ) 5) 4) 7)
TEOREMAS DEL VALOR MEDIO., entonces existe algún punto c (a, b) tal que f ( c)
 TEOREMAS DEL VALOR MEDIO Torma d Roll Si f () s continua n [a, b] y drivabl n (a, b), y si f (, ntoncs ist algún punto c (a, b) tal qu Intrprtación gométrica: ist un punto al mnos d s intrvalo, n l qu
TEOREMAS DEL VALOR MEDIO Torma d Roll Si f () s continua n [a, b] y drivabl n (a, b), y si f (, ntoncs ist algún punto c (a, b) tal qu Intrprtación gométrica: ist un punto al mnos d s intrvalo, n l qu
Análisis. b) Calcular razonadamente b y c para que sea derivable y calcular su función derivada.
 MATEMÁTICAS º BACHILLERATO B 6-3- Análisis OPCIÓN A.- Dada la función + b + c f = Ln( + ) > a) Calcular sus asínoas b) Calcular razonadamn b y c para qu sa drivabl y calcular su función drivada. a) El
MATEMÁTICAS º BACHILLERATO B 6-3- Análisis OPCIÓN A.- Dada la función + b + c f = Ln( + ) > a) Calcular sus asínoas b) Calcular razonadamn b y c para qu sa drivabl y calcular su función drivada. a) El
( ) 2. 1. Calcula las siguientes integrales. Soluciones. 1 x. arctan. x 4x + 13. sen x dx. x 2. 11arctan. x dx + 2. e x. e arctan e. e dx.
 Albrto Entro Cond Mait Gonzálz Juarrro Intgral indfinida Cálculo d primitivas Calcula las siguints intgrals Solucions A d A d + + + ln( + + ) A d arctan + A sn sn d A d ln ( ) 6A d cos tan + arctan + ln(
Albrto Entro Cond Mait Gonzálz Juarrro Intgral indfinida Cálculo d primitivas Calcula las siguints intgrals Solucions A d A d + + + ln( + + ) A d arctan + A sn sn d A d ln ( ) 6A d cos tan + arctan + ln(
TEMA 4. APLICACIONES DE LA DERIVADA.
 7 Unidad 4. Funcions. Aplicacions d la drivada TEMA 4. APICACIONES DE A DERIVADA.. Monotonía. Crciminto y dcrciminto d una función. Etrmos rlativos 3. Optimización 4. Curvatura 5. Punto d Inflión 6. Propidads
7 Unidad 4. Funcions. Aplicacions d la drivada TEMA 4. APICACIONES DE A DERIVADA.. Monotonía. Crciminto y dcrciminto d una función. Etrmos rlativos 3. Optimización 4. Curvatura 5. Punto d Inflión 6. Propidads
COMPUTACIÓN. Práctica nº 2
 Matmáticas Computación COMPUTACIÓN Práctica nº NÚMEROS REALES Eistn algunos númros irracionals prdfinidos n Maima como son l númro π l númro qu s corrspondn con los símbolos %pi % rspctivamnt. Otros númros
Matmáticas Computación COMPUTACIÓN Práctica nº NÚMEROS REALES Eistn algunos númros irracionals prdfinidos n Maima como son l númro π l númro qu s corrspondn con los símbolos %pi % rspctivamnt. Otros númros
Opción A Ejercicio 1 opción A, modelo Septiembre 2011
 IES Fco Ayala d Granada Sptimbr d 0 (Modlo ) Grmán-Jsús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 0-0 MATEMÁTICAS II Opción A Ejrcicio opción A, modlo Sptimbr 0 k si
IES Fco Ayala d Granada Sptimbr d 0 (Modlo ) Grmán-Jsús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 0-0 MATEMÁTICAS II Opción A Ejrcicio opción A, modlo Sptimbr 0 k si
ANÁLISIS (Selectividad 2014) 1
 ANÁLISIS (Slctividad 4) ALGUNOS PROBLEMAS DE ANÁLISIS PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD EN 4 ( Obsrvación: La slcción s ha hcho dando prioridad a las custions más tóricas) Andalucía, junio 4 San
ANÁLISIS (Slctividad 4) ALGUNOS PROBLEMAS DE ANÁLISIS PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD EN 4 ( Obsrvación: La slcción s ha hcho dando prioridad a las custions más tóricas) Andalucía, junio 4 San
I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL. PRIMERA EVALUACIÓN. ANÁLISIS
 Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
= 1. x = 3: Lím = Asíntota vertical en x = 3: = 0 ; No se anula nunca. Punto de corte con OY es (0, 3) 3 x
 Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
CARACTERÍSTICAS EXTERNAS y REGULACIÓN de TRANSFORMADORES
 CARACTERÍSTCAS EXTERNAS y REGLACÓN d TRANSFORMADORES Norbrto A. Lmozy 1 CARACTERÍSTCAS EXTERNAS S dnomina variabl ntr a una magnitud qu stá dtrminada ntr dos puntos, tal como una difrncia d potncial o
CARACTERÍSTCAS EXTERNAS y REGLACÓN d TRANSFORMADORES Norbrto A. Lmozy 1 CARACTERÍSTCAS EXTERNAS S dnomina variabl ntr a una magnitud qu stá dtrminada ntr dos puntos, tal como una difrncia d potncial o
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
 LÍMITES DE FUNCIONES. CONTINUIDAD RAMAS INFINITAS Página 7 REFLEIONA RESUELVE Aproimaciones sucesivas Comprueba que: f () =,5; f (,9) =,95; f (,99) =,995 Calcula f (,999); f (,9999); f (,99999); A la vista
LÍMITES DE FUNCIONES. CONTINUIDAD RAMAS INFINITAS Página 7 REFLEIONA RESUELVE Aproimaciones sucesivas Comprueba que: f () =,5; f (,9) =,95; f (,99) =,995 Calcula f (,999); f (,9999); f (,99999); A la vista
PRÁCTICA 8 ESTUDIO DE ENGRANAJES 3º INGENIERÍA INDUSTRIAL
 PRÁCTICA 8 ESTUDIO DE ENGRANAJES 3º INGENIERÍA INDUSTRIAL 1.- INTRODUCCIÓN. La prsnt práctica tin por objto introduir al alumno n l cálculo d trns d ngranajs, tanto simpls d js parallos, compustos y trns
PRÁCTICA 8 ESTUDIO DE ENGRANAJES 3º INGENIERÍA INDUSTRIAL 1.- INTRODUCCIÓN. La prsnt práctica tin por objto introduir al alumno n l cálculo d trns d ngranajs, tanto simpls d js parallos, compustos y trns
TEMA 8: LÍMITES DE FUNCIONES. CONTINUIDAD
 TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
La variable independiente x es aquella cuyo valor se fija previamente. La variable dependiente y es aquella cuyo valor se deduce a partir de x.
 Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
Bloque II. Actividades de síntesis: Análisis. Solucionario OPCIÓN A
 Bloque II Actividades de síntes: Anális Solucionario OPCIÓN A A.. a) Escribe la función f(x) x 4 x como una función a trozos y dibuja su gráfica. b) Para cuántos valores de x es f(x) 0? c) Para qué números
Bloque II Actividades de síntes: Anális Solucionario OPCIÓN A A.. a) Escribe la función f(x) x 4 x como una función a trozos y dibuja su gráfica. b) Para cuántos valores de x es f(x) 0? c) Para qué números
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL
 APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL 74 Cuando un problma gométrico stá nunciado n términos d la rcta
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL 74 Cuando un problma gométrico stá nunciado n términos d la rcta
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
 LÍMITES DE FUNCIONES. CONTINUIDAD RAMAS INFINITAS Página 7 REFLEIONA RESUELVE Aproimaciones sucesivas Comprueba que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
LÍMITES DE FUNCIONES. CONTINUIDAD RAMAS INFINITAS Página 7 REFLEIONA RESUELVE Aproimaciones sucesivas Comprueba que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
Método de los Elementos Finitos para Análisis Estructural. Alisado de tensiones
 Método d los Elmntos Finitos para Análisis Estructural Alisado d tnsions Campo d tnsions Tnsions n cualquir punto dl lmnto, sgún l MEF: = Dε= DBδ Matriz B contin las drivadas d las N: no son continuas
Método d los Elmntos Finitos para Análisis Estructural Alisado d tnsions Campo d tnsions Tnsions n cualquir punto dl lmnto, sgún l MEF: = Dε= DBδ Matriz B contin las drivadas d las N: no son continuas
LIMITES DE FUNCIONES EN 1D
 LIMITES DE FUNCIONES EN D Límits d funcions n D Autor: Patrici Molinàs Mata (pmolinas@uoc.du), José Francisco Martínz Boscá (jmartinzbos@uoc.du) ESQUEMA DE CONTENIDOS Dfinición Límits latrals LÍMITE DE
LIMITES DE FUNCIONES EN D Límits d funcions n D Autor: Patrici Molinàs Mata (pmolinas@uoc.du), José Francisco Martínz Boscá (jmartinzbos@uoc.du) ESQUEMA DE CONTENIDOS Dfinición Límits latrals LÍMITE DE
Problemas de limites, continuidad y derivabilidad. Calcula los siguientes límites de funciones racionales, irracionales y exponenciales
 Problemas de limites, continuidad y derivabilidad Calcula los siguientes límites de funciones racionales, irracionales y eponenciales - ) = [ = = = = = = = . ) = [0. ] = = = = = = = = = 0 = [ = p=
Problemas de limites, continuidad y derivabilidad Calcula los siguientes límites de funciones racionales, irracionales y eponenciales - ) = [ = = = = = = = . ) = [0. ] = = = = = = = = = 0 = [ = p=
ALGUNOS PROBLEMAS DE ANÁLISIS PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2015
 ANÁLISIS (Slctividad 5) ALGUNOS PROBLEMAS DE ANÁLISIS PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 5 Andalucía, junio 5 Sa f la función dfinida por f( ) para a) [ punto] Estudia y calcula las asíntotas
ANÁLISIS (Slctividad 5) ALGUNOS PROBLEMAS DE ANÁLISIS PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 5 Andalucía, junio 5 Sa f la función dfinida por f( ) para a) [ punto] Estudia y calcula las asíntotas
Estas pruebas permiten verificar que la población de la cual proviene una muestra tiene una distribución especificada o supuesta.
 PRUEBAS DE BONDAD DE AJUSTE Estas prubas prmitn vrificar qu la población d la cual provin una mustra tin una distribución spcificada o supusta. Sa X: variabl alatoria poblacional f 0 (x) la distribución
PRUEBAS DE BONDAD DE AJUSTE Estas prubas prmitn vrificar qu la población d la cual provin una mustra tin una distribución spcificada o supusta. Sa X: variabl alatoria poblacional f 0 (x) la distribución
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS
 CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS 14-1 Los tipos d intrés nominals y rals Slid 14.2 Los tipos d intrés xprsados n unidads d la monda nacional s dnominan tipos d intrés nominals. Los
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS 14-1 Los tipos d intrés nominals y rals Slid 14.2 Los tipos d intrés xprsados n unidads d la monda nacional s dnominan tipos d intrés nominals. Los
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO. Análisis Matemático
 Análisis Matemático Unidad 4 - Límite de una función en un punto Límite de una función en un punto El límite de una función para un valor de x es el valor al que la función tiende en los alrededores de
Análisis Matemático Unidad 4 - Límite de una función en un punto Límite de una función en un punto El límite de una función para un valor de x es el valor al que la función tiende en los alrededores de
5. Convergencia de integrales impropias. Las funciones Γ y Β de Euler.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lcción. Intgals y aplicacions. 5. Convgncia d intgals impopias. Las funcions Γ y Β d Eul. La foma haitual d calcula una intgal impopia, po jmplo dl intgando, aplica
GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lcción. Intgals y aplicacions. 5. Convgncia d intgals impopias. Las funcions Γ y Β d Eul. La foma haitual d calcula una intgal impopia, po jmplo dl intgando, aplica
Colegio Portocarrero. Curso Departamento de matemáticas. Limites, asíntotas y continuidad
 Limites, asíntotas y continuidad Problema 1: Sea la función. Determina las asíntotas si existen. Problema 2: Dada la función a) Representa gráficamente f(x) b) Estudia su continuidad. Problema 3: Un inversor
Limites, asíntotas y continuidad Problema 1: Sea la función. Determina las asíntotas si existen. Problema 2: Dada la función a) Representa gráficamente f(x) b) Estudia su continuidad. Problema 3: Un inversor
INSTITUTO TECNOLÓGICO DE COSTA RICA ESCUELA DE INGENIERÍA ELECTRÓNICA CURSO: MODELOS DE SISTEMAS CÁLCULO DE RESIDUOS Y SUS APLICACIONES
 INSTITUTO TENOLÓGIO DE OSTA RIA ESUELA DE INGENIERÍA ELETRÓNIA URSO: MODELOS DE SISTEMAS ÁLULO DE RESIDUOS Y SUS APLIAIONES ING. FAUSTINO MONTES DE OA FEBRERO DE álculo d Rsiduos y sus Aplicacions INDIE
INSTITUTO TENOLÓGIO DE OSTA RIA ESUELA DE INGENIERÍA ELETRÓNIA URSO: MODELOS DE SISTEMAS ÁLULO DE RESIDUOS Y SUS APLIAIONES ING. FAUSTINO MONTES DE OA FEBRERO DE álculo d Rsiduos y sus Aplicacions INDIE
Gráficas de funciones
 Apuntes Tema 1 Gráficas de funciones 1.1 Gráficas de funciones a) Función constante: f(x) = k b) Recta vertical: x = k c) Función lineal: f(x) = mx Todas pasan por el origen O(0, 0). 2 d) Función afín:
Apuntes Tema 1 Gráficas de funciones 1.1 Gráficas de funciones a) Función constante: f(x) = k b) Recta vertical: x = k c) Función lineal: f(x) = mx Todas pasan por el origen O(0, 0). 2 d) Función afín:
INSTITUTO POLITECNICO NACIONAL PROBLEMARIO DE CALCULO DIFERENCIAL E INTEGRAL
 INSTITUTO POLITECNICO NACIONAL UNIDAD PROFESIONAL INTERDISCIPLINARIA DE BIOTECNOLOGIA PROBLEMARIO DE CALCULO DIFERENCIAL E INTEGRAL ELABORO: PROF. MARIO CERVANTES CONTRERAS DICIEMBRE DE 7 EJERCICIOS DE
INSTITUTO POLITECNICO NACIONAL UNIDAD PROFESIONAL INTERDISCIPLINARIA DE BIOTECNOLOGIA PROBLEMARIO DE CALCULO DIFERENCIAL E INTEGRAL ELABORO: PROF. MARIO CERVANTES CONTRERAS DICIEMBRE DE 7 EJERCICIOS DE
Capítulo V CONDICIONES DE FRONTERA Y MODELAMIENTO NUMÉRICO EN ECUACIONES DIFERENCIALES
 Marclo Romo Proaño Escula Politécnica dl Ejército - Ecuador Capítulo V CONDICIONES DE FRONTERA Y MODELAMIENTO NUMÉRICO EN ECUACIONES DIFERENCIALES 5. CONDICIONES DE FRONTERA: Dbido a qu muchos problmas
Marclo Romo Proaño Escula Politécnica dl Ejército - Ecuador Capítulo V CONDICIONES DE FRONTERA Y MODELAMIENTO NUMÉRICO EN ECUACIONES DIFERENCIALES 5. CONDICIONES DE FRONTERA: Dbido a qu muchos problmas
Ejemplo: Resolvemos Sin solución. O siempre es positiva o siempre es negativa. Damos un valor cualquiera Siempre + D(f) =
 T1 Dominios, Límites, Asíntotas, Derivadas y Representación Gráfica. 1.1 Dominios de funciones: Polinómicas: D( = La X puede tomar cualquier valor entre Ejemplos: D( = Función racional: es el cociente
T1 Dominios, Límites, Asíntotas, Derivadas y Representación Gráfica. 1.1 Dominios de funciones: Polinómicas: D( = La X puede tomar cualquier valor entre Ejemplos: D( = Función racional: es el cociente
Continuidad y ramas infinitas. El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A = 2. lm í
 Unidad. Límites de funciones. Continuidad y ramas infinitas Resuelve Página 7 A través de una lupa AUMENTO DISTANCIA (dm) El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A
Unidad. Límites de funciones. Continuidad y ramas infinitas Resuelve Página 7 A través de una lupa AUMENTO DISTANCIA (dm) El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A
Continuidad, límites y asíntotas
 9 Continuidad, ites y asíntotas. Funciones especiales Piensa y calcula Completa la siguiente tabla: Parte entera de Parte decimal de Valor absoluto de 0,3 0,3,8,8 2,4 2,4 3,9 Ent () Dec () 3,9 0,3 0,3,8,8
9 Continuidad, ites y asíntotas. Funciones especiales Piensa y calcula Completa la siguiente tabla: Parte entera de Parte decimal de Valor absoluto de 0,3 0,3,8,8 2,4 2,4 3,9 Ent () Dec () 3,9 0,3 0,3,8,8
FUNCIONES EXPONENCIAL, LOGARÍTMICA Y SUS DERIVADAS.
 Prof., Enriqu Matus Nivs Doctorano n Eucación Matmática. FUNCIONES EXPONENCIAL, LOGARÍTMICA Y SUS DERIVADAS. Una función ponncial s aqulla n la qu la variabl stá n l ponnt. Algunos - - -5 jmplos funcions
Prof., Enriqu Matus Nivs Doctorano n Eucación Matmática. FUNCIONES EXPONENCIAL, LOGARÍTMICA Y SUS DERIVADAS. Una función ponncial s aqulla n la qu la variabl stá n l ponnt. Algunos - - -5 jmplos funcions
Límite y continuidad de una función
 UNIDAD Límite y continuidad de una función E n esta Unidad, de forma descriptiva, sin usar un aparato matemático ecesivamente riguroso, aunque manejando la notación habitual, se introduce el cálculo infinitesimal:
UNIDAD Límite y continuidad de una función E n esta Unidad, de forma descriptiva, sin usar un aparato matemático ecesivamente riguroso, aunque manejando la notación habitual, se introduce el cálculo infinitesimal:
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
Problemas de Asíntotas de funciones
 www.vaasoftware.com/gp 1) Determinar las asíntotas verticales de la siguiente función y estudiar la posición de la 1 + 5 ) Determinar las asíntotas verticales de la siguiente función y estudiar la posición
www.vaasoftware.com/gp 1) Determinar las asíntotas verticales de la siguiente función y estudiar la posición de la 1 + 5 ) Determinar las asíntotas verticales de la siguiente función y estudiar la posición
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
CAPITULO 5. ECUACIONES DIFERENCIALES DE ORDEN N 2. 5.1. Introducción. 5.2. Reducción de orden
 APITULO 5. EUAIONES DIFERENIALES DE ORDEN N 5.. Introducción Una cuación difrncial d sgundo ordn s una prsión matmática n la qu s rlaciona una función con sus drivadas primra sgunda. Es dcir, una prsión
APITULO 5. EUAIONES DIFERENIALES DE ORDEN N 5.. Introducción Una cuación difrncial d sgundo ordn s una prsión matmática n la qu s rlaciona una función con sus drivadas primra sgunda. Es dcir, una prsión
MATEMÁTICAS II PRUEBAS DE ACCESO A LA UNIVERSIDAD DE OVIEDO
 MTEMÁTICS II PRUEBS DE CCESO L UNIVERSIDD DE OVIEDO.- NÁLISIS ª PRTE.- Cálclo Intgral.- MODELO DE PRUEB Dada la parábola, s corta por la rcta d cación ; n los pntos d intrscción s trazan las tangnts a
MTEMÁTICS II PRUEBS DE CCESO L UNIVERSIDD DE OVIEDO.- NÁLISIS ª PRTE.- Cálclo Intgral.- MODELO DE PRUEB Dada la parábola, s corta por la rcta d cación ; n los pntos d intrscción s trazan las tangnts a
Tema 3 La elasticidad y sus aplicaciones
 Ejrcicios rsultos d Introducción a la Toría Económica Carmn olors Álvarz Alblo Migul Bcrra omínguz Rosa María Cácrs Alvarado María dl Pilar Osorno dl Rosal Olga María Rodríguz Rodríguz Tma 3 La lasticidad
Ejrcicios rsultos d Introducción a la Toría Económica Carmn olors Álvarz Alblo Migul Bcrra omínguz Rosa María Cácrs Alvarado María dl Pilar Osorno dl Rosal Olga María Rodríguz Rodríguz Tma 3 La lasticidad
Límites y continuidad de funciones reales de variable real
 Límites y continuidad de funciones reales de variable real Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 10 2.1. Funciones
Límites y continuidad de funciones reales de variable real Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 10 2.1. Funciones
Tema 8. Limite de funciones. Continuidad
 . Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
UNIDAD 1: LÍMITES DE FUNCIONES. CONTINUIDAD
 UNIDAD : LÍMITES Y CONTINUIDAD UNIDAD : LÍMITES DE FUNCIONES CONTINUIDAD ÍNDICE DE LA UNIDAD - INTRODUCCIÓN - LÍMITE DE UNA FUNCIÓN EN UN PUNTO LÍMITES LATERALES - LÍMITES EN EL INFINITO 5 4- ÁLGEBRA DE
UNIDAD : LÍMITES Y CONTINUIDAD UNIDAD : LÍMITES DE FUNCIONES CONTINUIDAD ÍNDICE DE LA UNIDAD - INTRODUCCIÓN - LÍMITE DE UNA FUNCIÓN EN UN PUNTO LÍMITES LATERALES - LÍMITES EN EL INFINITO 5 4- ÁLGEBRA DE
9 TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO
 9 TRSLINES, GIRS SIMETRÍS EN EL PLN EJERIIS PRPUESTS 9. ibuja un parallogramo y razona qué pars d vctors dtrminados por los vértics son quipolnts. Son quipolnts los qu son parallos y dl mismo sntido, y
9 TRSLINES, GIRS SIMETRÍS EN EL PLN EJERIIS PRPUESTS 9. ibuja un parallogramo y razona qué pars d vctors dtrminados por los vértics son quipolnts. Son quipolnts los qu son parallos y dl mismo sntido, y
Límites y continuidad
 Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
Ejercicios de representación de funciones
 Ejercicios de representación de funciones 1.- Representar las siguientes funciones, estudiando su: Dominio. Simetría. Puntos de corte con los ejes. Asíntotas y ramas parabólicas. Crecimiento y decrecimiento.
Ejercicios de representación de funciones 1.- Representar las siguientes funciones, estudiando su: Dominio. Simetría. Puntos de corte con los ejes. Asíntotas y ramas parabólicas. Crecimiento y decrecimiento.
Estudio Gráfico de Funciones
 Esquema 1 2 Esquema 1 2 Definición es una correspondencia entre dos conjuntos A B tal que a cada elemento del conjunto A le corresponde un único valor solo uno del conjunto B. La gráfica de la función
Esquema 1 2 Esquema 1 2 Definición es una correspondencia entre dos conjuntos A B tal que a cada elemento del conjunto A le corresponde un único valor solo uno del conjunto B. La gráfica de la función
Límite de una función
 Límite de una función Idea intuitiva de límite El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
Límite de una función Idea intuitiva de límite El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
DERIVADAS LECCIÓN 22. Índice: Representación gráfica de funciones. Problemas. 1.- Representación gráfica de funciones
 DERIVADAS LECCIÓN Índice: Representación gráfica de funciones. Problemas.. Representación gráfica de funciones Antes de la representación de la gráfica de una función se realiza el siguiente estudio: º)
DERIVADAS LECCIÓN Índice: Representación gráfica de funciones. Problemas.. Representación gráfica de funciones Antes de la representación de la gráfica de una función se realiza el siguiente estudio: º)
Energía. Reactivos. Productos. Coordenada de reacción
 CINÉTICA QUÍMICA 1 - Razon: a) Si pud dducirs, a partir d las figuras corrspondints, si las raccions rprsntadas n (I) y (II) son d igual vlocidad y si, prvisiblmnt, srán spontánas. b) En la figura (III)
CINÉTICA QUÍMICA 1 - Razon: a) Si pud dducirs, a partir d las figuras corrspondints, si las raccions rprsntadas n (I) y (II) son d igual vlocidad y si, prvisiblmnt, srán spontánas. b) En la figura (III)
Solución. - Verticales: En los puntos excluidos del dominio donde el límite quede de la forma k. 3( ) = Asíntota vertical. = + x 2.
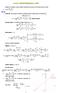 Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
ANÁLISIS DEL AMPLIFICADOR EN EMISOR COMÚN
 ANÁLISIS DL AMPLIFIADO N MISO OMÚN Jsús Pizarro Pláz. INTODUIÓN... 2. ANÁLISIS N ONTINUA... 2 3. TA D AGA N ALTNA... 3 4. IUITO QUIALNT D ALTNA... 4 5. FUNIONAMINTO... 7 NOTAS... 8. INTODUIÓN l amplificador
ANÁLISIS DL AMPLIFIADO N MISO OMÚN Jsús Pizarro Pláz. INTODUIÓN... 2. ANÁLISIS N ONTINUA... 2 3. TA D AGA N ALTNA... 3 4. IUITO QUIALNT D ALTNA... 4 5. FUNIONAMINTO... 7 NOTAS... 8. INTODUIÓN l amplificador
http://www.cepamarm.es ACFGS - Matemáticas ESG - 05/2013 Pág. 1 de 17
 http://www.cepamarm.es ACFGS - Matemáticas ESG - 05/2013 Pág. 1 de 17 1 CONCEPTOS BÁSICOS 1.1 DEFINICIONES Una función liga dos variables numéricas a las que, habitualmente, se les llama x e y. x es la
http://www.cepamarm.es ACFGS - Matemáticas ESG - 05/2013 Pág. 1 de 17 1 CONCEPTOS BÁSICOS 1.1 DEFINICIONES Una función liga dos variables numéricas a las que, habitualmente, se les llama x e y. x es la
Ejercicios de Funciones, límites y continuidad.
 Matemáticas 1ºBach CNyT. Ejercicios Funciones. Pág 1/12 Ejercicios de Funciones, límites y continuidad. 1. Estudia el dominio de las siguientes funciones 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
Matemáticas 1ºBach CNyT. Ejercicios Funciones. Pág 1/12 Ejercicios de Funciones, límites y continuidad. 1. Estudia el dominio de las siguientes funciones 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
PROBLEMAS DE INTEGRALES INDEFINIDAS
 PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
Sistemas de control: Elementos componentes, variables, función de transferencia y diagrama funcional.
 Sistmas d control: Elmntos componnts, variabls, función d transfrncia y diagrama funcional. Introducción Los sistmas d control automático han jugado un papl vital n l avanc d la cincia y d la ingniría.
Sistmas d control: Elmntos componnts, variabls, función d transfrncia y diagrama funcional. Introducción Los sistmas d control automático han jugado un papl vital n l avanc d la cincia y d la ingniría.
Matemáticas 1º Bachillerato ASÍNTOTAS Colegio La Presentación
 ASÍNTOTA Es una recta imaginaria que nosotros calculamos y representamos con una línea discontinua. Esta recta tiene la propiedad de que en el infinito no puede ser traspasada por la gráfica de la función,
ASÍNTOTA Es una recta imaginaria que nosotros calculamos y representamos con una línea discontinua. Esta recta tiene la propiedad de que en el infinito no puede ser traspasada por la gráfica de la función,
TAMAÑO DE LA MUESTRA
 Rv. Epidm. Md. Prv. (003), : 8-4 TAMAÑO DE LA MUESTRA Enric Matu, Jordi Casal CRSA. Cntr d Rcrca n Sanitat Animal / Dp. Sanitat i Anatomia Animals, Univrsitat Autònoma d Barclona, 0893-Bllatrra, Barclona
Rv. Epidm. Md. Prv. (003), : 8-4 TAMAÑO DE LA MUESTRA Enric Matu, Jordi Casal CRSA. Cntr d Rcrca n Sanitat Animal / Dp. Sanitat i Anatomia Animals, Univrsitat Autònoma d Barclona, 0893-Bllatrra, Barclona
FUNCIONES Y GRÁFICAS.
 FUNCIONES Y GRÁFICAS. CONTENIDOS: Concepto de función. Gráfica de una función. Estudio cualitativo de funciones dadas por sus gráficas Idea intuitiva de continuidad de una función. Repaso de funciones
FUNCIONES Y GRÁFICAS. CONTENIDOS: Concepto de función. Gráfica de una función. Estudio cualitativo de funciones dadas por sus gráficas Idea intuitiva de continuidad de una función. Repaso de funciones
Tema 7. Límites y continuidad de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Aplicaciones de la integral definida al cálculo de áreas
 Aplicaciones de la integral definida al cálculo de áreas 1º) Interpreta geométricamente el área que define la integral y obtenla. Geométricamente, la integral representa el área de la región del plano
Aplicaciones de la integral definida al cálculo de áreas 1º) Interpreta geométricamente el área que define la integral y obtenla. Geométricamente, la integral representa el área de la región del plano
ASÍNTOTAS DE LA GRÁFICA DE UNA FUNCIÓN
 ASÍNTOTAS DE LA GRÁFICA DE UNA FUNCIÓN La gráfica de una función elemental puede presentar ninguna una o varias asíntotas verticales y además puede presentar a lo sumo una asíntota horizontal o una asíntota
ASÍNTOTAS DE LA GRÁFICA DE UNA FUNCIÓN La gráfica de una función elemental puede presentar ninguna una o varias asíntotas verticales y además puede presentar a lo sumo una asíntota horizontal o una asíntota
Análisis de funciones y representación de curvas
 12 Análisis de funciones y representación de curvas 1. Análisis gráfico de una función Aplica la teoría 1. Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario
12 Análisis de funciones y representación de curvas 1. Análisis gráfico de una función Aplica la teoría 1. Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario
ANÁLISIS DE FUNCIONES, LÍMITES Y CONTINUIDAD. RESUMEN
 ANÁLISIS DE FUNCIONES, LÍMITES Y CONTINUIDAD. RESUMEN Problema Datos Procedimiento Ejemplo Dominio de una La ecuación de Casos en los que en dominio no es IR: función la función Irracionales (ecluir valores
ANÁLISIS DE FUNCIONES, LÍMITES Y CONTINUIDAD. RESUMEN Problema Datos Procedimiento Ejemplo Dominio de una La ecuación de Casos en los que en dominio no es IR: función la función Irracionales (ecluir valores
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
UNA INVITACIÓN AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES ORDINARIAS. Maritza de Franco
 UNA INVITACIÓN AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES ORDINARIAS. Marita d Franco A Francisco José, Shrl, Marión, Paola, Constanc, Luis Migul Migul. AGRADECIMIENTOS Al Ing. Pdro Rangl por su comprnsión,
UNA INVITACIÓN AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES ORDINARIAS. Marita d Franco A Francisco José, Shrl, Marión, Paola, Constanc, Luis Migul Migul. AGRADECIMIENTOS Al Ing. Pdro Rangl por su comprnsión,
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
Áreas entre curvas. Ejercicios resueltos
 Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
