Juan José Font Ferrandis. Salvador Hernández Muñoz. Sergio Macario Vives
|
|
|
- Francisco Sandoval Villalba
- hace 7 años
- Vistas:
Transcripción
1 CÁLCULO Jua José Fot Ferradis Salvador Herádez Muñoz Sergio Macario Vives
2 Ídice geeral. Campos Numéricos.. El úmero real Desigualdades Valor absoluto de u úmero real El úmero complejo Aritmética de los úmeros complejos Módulo y argumeto de u úmero complejo Raíces eteras de u úmero complejo Expoecial compleja y Logaritmo complejo Problemas adicioales Sucesioes Numéricas Sucesioes reales. Subsucesioes Sucesioes moótoas Sucesioes acotadas Sucesioes covergetes i
3 2.5. Cálculo de límites Ifiitésimos Ifiitos Problemas adicioales Series Numéricas Series reales Criterios de covergecia Series de térmios positivos Series alteradas Covergecia absoluta y codicioal Sumació de series Problemas adicioales Series de Potecias Radio de covergecia Propiedades Desarrollo de fucioes e serie de potecias Desarrollos de Taylor Otros desarrollos Problemas adicioales Fucioes de varias variables Represetació de fucioes ii
4 5.2. Fucioes vectoriales Límites y cotiuidad Límites Fucioes cotiuas Problemas adicioales Fucioes difereciables Derivadas parciales La diferecial Plaos tagetes Matriz Jacobiaa Derivadas direccioales Derivadas parciales de orde superior Regla de la cadea Problemas adicioales Teoremas del cálculo diferecial Teorema del valor medio Teorema de Taylor Teorema de la Fució Iversa Teorema de la Fució Implícita Problemas adicioales Extremos 66 iii
5 8.. Extremos libres Extremos codicioados Método de reducció de variables Método de multiplicadores de Lagrage Máximos y míimos absolutos Problemas adicioales Itegració Defiicioes básicas Itegral superior e iferior de Darboux Teorema de caracterizació Propiedades de la Itegral Reglas de itegració y Teorema del Valor Medio Fució itegral. Regla de Barrow Itegració por partes y sustitució Aplicacioes Problemas adicioales Itegrales dobles y triples Itegrales dobles sobre rectágulos Cálculo de itegrales dobles Itegrales dobles sobre recitos acotados Cálculo de áreas iv
6 0.2. Itegrales triples Itegració sobre recitos acotados Cambio de variable Problemas adicioales Tabla de primitivas 244 Bibliografía 248 v
7 Ídice de figuras.. Represetació cartesiaa de u úmero complejo Módulo y argumeto de u úmero complejo Represetació gráfica de ua sucesió Sucesió decreciete Sucesió creciete Sucesió acotada a M Sucesió covergete Sucesió divergete Aproximació a e x por su serie de potecias Secció trasversal co x fija Curvas de ivel de z = 4 x y Curvas de ivel de z = x 2 + y Superficies de ivel de x 2 + y 2 + z Superficies de ivel de z x 2 + y vi
8 5.6. Campo vectorial Gráfica de si( x ) Iterpretació geométrica de la derivada parcial El gradiete es perpedicular a las curvas de ivel Plao tagete Iterpretació geométrica de la derivada direccioal Tipos de extremos Gráfica de z = x 5 y + xy 5 + xy Gráfica de z = x 2 y Extremos de la fució restrigida Extremos e u recito triagular Sumas superior e iferior Suma para los putos medios Área etre dos curvas Área etre dos curvas que se corta Sólido de revolució geerado por ua cicloide Mallado para la aproximació del área Ua partició del rectágulo R = [a, b] [c, d] Sumas de Riema El teorema de Fubii vii
9 0.5. Recito acotado y fució característica Alguos domiios de tipo I Itegració sobre ua regió de tipo I Alguos domiios de tipo II Itegració sobre ua regió de tipo II U triágulo como regió de tipo I y II Área etre dos gráficas Área etre dos gráficas Disco uidad Volume de u tetraedro U aillo circular Itegració e coordeadas polares Volume de u cilidro circular Ua rosa de cuatro pétalos Disco uidad Coordeadas cilídricas Itegració sobre u semicoo Coordeadas esféricas viii
10 Prólogo El presete maual pretede proporcioar a los estudiates de primer curso de igeiería u texto de cosulta sobre ua parte de los fudametos matemáticos de cálculo diferecial e itegral. Destiado, e pricipio, a estudiates de las igeierías iformáticas, los coteidos se estructura e tres grades bloques: ua primera parte, Capítulos al 4, dedicada al estudio de la parte discreta del cálculo; es decir, las sucesioes y las series uméricas; ua parte cetral, Capítulos 5 al 9, co el estudio del cálculo diferecial de fucioes de varias variables reales y ua parte fial, Capítulos y 2, dedicada al estudio del cálculo itegral e ua y varias variables. Queda claro e estos coteidos que el cálculo diferecial de fucioes de ua variable real es prerrequisito imprescidible para abordar la lectura de este volume. Este coocimieto se supoe coocido de los cursos previos al acceso a la uiversidad. No obstate, e la bibliografía aparece varios textos dode el estudiate iteresado podría cosultar y repasar los resultados básicos del cálculo e ua variable, si ello fuere ecesario. Los capítulos que coforma el maual, sigue ua estructura de itroducció de coceptos teóricos co ejemplos resueltos de aplicació, dode el estudiate pueda y, seguramete, deba observar la metodología empleada e su resolució y cuestioarse el porqué de dicha metodología, como base para su apredizaje. Posteriormete, se preseta alguos ejercicios adicioales para que el alumo pueda practicar la metodología apredida y profudizar e el coocimieto de las ocioes desarrolladas. Tambié se icluye, al fial de cada capítulo, alguos ejercicios adicioales de dificultad variable destiados tato a reforzar lo apredido, como a estimular la búsqueda de solucioes alterativas. Pesado e gra medida como material de apoyo para las clases semipreseix
11 ciales, este maual cotribuye a dotar al estudiate de uos aputes de clase que, e igú caso, debería substituir el uso de otros textos mucho más elaborados y que se reseña al fial. La estructura de este texto está dirigida, pricipalmete, a que pueda servir al estudiate para su trabajo fuera del aula: eteder los ejemplos y la metodología de resolució y practicar co otros ejercicios de dificultad similar. E defiitiva, los autores cofiamos e que esta modesta cotribució ayude a uestros alumos a adquirir los coocimietos y las destrezas ecesarias para abordar la mayoría de los problemas del cálculo diferecial e itegral. Las figuras que acompaña el texto ha sido realizadas, salvo cotadas excepcioes, co el programa SAGE ( u proyecto de software matemático libre iiciado e la Uiversidad de Washigto. No obstate, se ha utilizado el programa Mathematica e alguas figuras y atiguos materiales de los autores. Tambié queremos agradecer la colaboració prestada por Óscar Muñoz e la trascripció y maquetado de este texto. x
12 Tema Campos Numéricos Se supoe al lector familiarizado co las propiedades usuales de los úmeros aturales N, los úmeros eteros Z y los úmeros racioales Q. Los úmeros aturales so los que utilizamos para cotar 0,, 2,.... Los úmeros eteros se obtiee al añadir a los ateriores los úmeros egativos, 2,... Los úmeros racioales so las fraccioes o proporcioes de úmeros eteros 2, 3 4, 2 5,.... Como cada úmero etero m puede ser escrito como la fracció m, se tiee las iclusioes N Z Q Los úmeros racioales además admite ua expresió decimal fiita o periódica. Pero ya desde muy atiguo es sabido que existe úmeros que o so así; por ejemplo, 2. A los úmeros que tiee ua represetació decimal ifiita y o periódica se les llama úmeros irracioales. Al cojuto de los úmeros racioales e irracioales se les llama úmeros reales R y sus propiedades va a jugar u papel primordial e todos los temas de este texto, puesto que vamos a estudiar fucioes cuyas variables va a ser, precisamete, úmeros reales debido a que represeta catidades que puede medirse. Si embargo, muchos feómeos físicos y químicos o puede formularse adecuadamete si coocer los úmeros complejos C. Auque u estudio pormeorizado de estos úmeros queda fuera del ámbito de este texto, sí que haremos ua pequeña itroducció a ellos e este tema para coocer alguas de sus propiedades.
13 .. El úmero real Todo y que la costrucció de los úmeros reales a partir de los úmeros racioales es iteresate por ella misma, queda fuera del ivel que se pretede coseguir e este maual. Por tato, os limitaremos a decir que los úmeros reales está formados por los úmeros racioales y los irracioales.... Desigualdades El cojuto de los úmeros reales, que deotaremos por R, tiee la estructura de cuerpo ordeado y la relació de orde la represetaremos por (la leeremos meor o igual que). Si dos úmeros reales, x, y verifica la relació x y pero x y etoces escribiremos x < y (y lo leeremos x meor que y). Eumeramos a cotiuació alguas de las propiedades relativas al comportamieto del orde frete a las operacioes aritméticas: x y x + z y + z z R x y z 0 zx zy x y z 0 zx zy 0 < x < y x > y Ejemplo. Prueba la desigualdad a 2 + b 2 2ab. Solució: Probamos e primer lugar que todo cuadrado es siempre o egativo; es decir, a 2 0 para todo a R. E efecto, si a = 0 es evidete que a 2 = 0 0; si a > 0 etoces a 2 = aa > a0 = 0 y, fialmete, si a < 0 etoces a 2 = aa > a0 = 0. Luego e cualquier caso a 2 0. Ahora, para probar la desigualdad del ejemplo, basta observar que debe ser (a b) 2 0 y, al desarrollar el cuadrado, (a b) 2 0 a 2 + b 2 2ab 0 a 2 + b 2 2ab 2
14 Las propiedades del orde permite resolver desigualdades de forma similar a como se resuelve las ecuacioes. La idea cosiste e aislar la variable x, co la diferecia de que la solució suele ser u itervalo o ua uió de itervalos. Ejemplo.2 Resuelve la desigualdad 4 < 2x 3 4. Solució: La iequació 4 < 2x 3 4 correspode e realidad a dos desigualdades 4 < 2x 3 y 2x 3 4; auque e este caso, podemos resolverlas cojutamete. La idea es aislar x, para ello empezamos sumado 3 a cada miembro de la desigualdad: 4 < 2x < 2x < 2x 7 Ahora dividiremos cada miembro por 2 y, siedo u úmero egativo, debemos cambiar el setido de las desigualdades: < 2x 7 2 > x que os da como solució el itervalo [ 7 2, 2 [ x < 2 Ejercicio. Resuelve la desigualdad 3x + > 2x + 2 y dibuja el cojuto solució e la recta real. (Sol.: ], + [. ) Ejercicio.2 Resuelve la desigualdad y dibuja el cojuto solució e la recta real: (a) x > x ; (b) x2 x (Sol.: (a) ], 0[ ], + [; (b) ] 3, [ ], + [. )..2. Valor absoluto de u úmero real Si x R, se defie el valor absoluto de x, y se deota por x, como x := x 2 Se puede comprobar que, etoces, tambié se cumple { x si x 0 x = x si x < 0 Alguas propiedades so 3
15 . x 0, x R 2. x = 0 x = 0 3. xy = x y, x, y R 4. x y = x, x, y R, y 0 y 5. x + y x + y, x R 6. x r r x r Ejemplo.3 Sea x, y úmeros reales. Prueba que máx{x, y} = x + y + y x 2 y mí{x, y} = x + y y x 2 Solució: Supoemos x y. Etoces, máx{x, y} = y. Por otra parte, x + y + y x 2 = x + y + (y x) 2 Además, mí{x, y} = x y, por otra parte, = 2y 2 = y. x + y y x 2 = x + y (y x) 2 = 2x 2 = x. La prueba e el otro caso, x > y, es totalmete aáloga. Ejemplo.4 Vamos a ecotrar el cojuto de putos de la recta real que verifica la desigualdad: 2x x 3 Solució: Aplicado la propiedad (6) aterior (tomado r = x 3 ) deducimos: 2x x 3 x 3 2x x 3 Distiguimos ahora dos posibilidades: x 3 (x 3) 2x x 3 3 x 2x 2x x 3 } 4
16 3 + 2x + x 2x x 3 } 4 3x x 2 } 4 3 x x 2 } No tiee solució. x < 3 ( (x 3)) 2x (x 3) x 3 2x 2x 3 x 3 2x x 2x + x 3 + } 2 x 3x 4 } x 2 x 4 3 } Es decir, x < 3 2 x 4 3 } 2 x 4 3 Así la solució es el itervalo [ 2, 4 3 ]. Ejercicio.3 Resuelve la desigualdad x 3 2x y expresa la solució como u itervalo. (Sol.: [ 2, 4 3 ] ) e el iter- Ejemplo.5 Vamos ahora a acotar la siguiete fució 2x + 3x valo ], 4[: Solució: Si x ], 4[ etoces < x < 4. A partir de esta desigualdad recostruimos la fució: < x < 4 2 < 2x < 8 3 < 2x + < 9 < x < 4 3 < 3x < 2 2 < 3x < 3 < 3x < 2 Así, 2 < 3x < 3 < 2x + < < 2x + 3x < 9 5
17 Ejercicio.4 Acota la fució f(x) = ex x e el itervalo < x < 4. (Sol.: f(x) < 27 y o acotada iferiormete ) Ejemplo.6 Prueba, por iducció fiita, que = ( + ). 2 Solució: Lo comprobamos para =, 2: = ( + ) 2(2 + ), + 2 = = Lo supoemos cierto para : = Lo probamos para + : ( + ) (+) = ( + ) ( + ) + 2( + ) ( + )( + 2) ++ = = Ejemplo.7 Prueba, por iducció fiita, que x = x, N. Solució: Lo comprobamos para =, 2: x = x, x 2 = xx = x x = x 2 Lo supoemos cierto para : x = x. Lo probamos para + : x + = x x = x x = x x = x + Ejercicio.5 Prueba, por iducció fiita, que 2 >, N. Ejercicio.6 Prueba, por iducció fiita, que = 7, para cada ; es decir, es de la forma 7k para u etero k (múltiplo de 7). 6
18 .2. El úmero complejo El cojuto de los úmero complejos, que deotaremos por C, tiee estructura de cuerpo y puede idetificarse co R 2, de tal forma que cualquier úmero complejo se puede escribir de la forma z = a + bi siedo a y b úmero reales y siedo i la uidad imagiaria (la cual viee defiida por la igualdad i 2 = ). Al úmero a se le llama parte real de z y se represeta por R(z); al úmero b se le llama parte imagiaria de z y se represeta por I(z). Todo úmero complejo se puede idetificar co u puto del plao cartesiao R 2 de coordeadas (a, b) (Fig.). A la expresió z = a + bi se le llama expresió biómica de z. Figura.: Represetació cartesiaa de u úmero complejo..2.. Aritmética de los úmeros complejos Vamos a defiir ahora la suma y el producto de úmeros complejos. Si z = a + bi y w = c + di etoces defiimos z + w := (a + c) + (b + d)i z w := (ac bd) + (ad + bc)i 7
19 Notad que e realidad la suma y el producto se hace como si se tratara de biomios, por ejemplo, z w = (a + bi)(c + di) = ac + adi + bci + bdi 2 = ac bd + (ad + bc)i Defiició. Si z = a + bi llamaremos cojugado de z a z = a bi Ejemplo.8 Veamos como desarrollar potecias y cocietes. ( 2i) 2 = 2 + (2i) 2 2 2i = 4 4i = 3 4i i ( i)( i) = + i ( + i)( i) = + i2 2i i 2 = 2i 2 = i Ejercicio.7 Expresa e forma biómica los complejos w = i y w 2 = ( i)2 i 2i. (Sol.: w = i y w 2 = i ) Ejercicio.8 Expresar el complejo ( i)4 + i e forma biómica. (Sol.: i ).2.2. Módulo y argumeto de u úmero complejo Si z = a+bi, llamaremos módulo de z, y lo deotaremos como z, al úmero real z = a 2 + b 2 Alguas propiedades del módulo so. z 0, z C 2. z = 0 z = 0 3. z w = z w, z, w C 8
20 4. z =, z z C, z 0 5. z + w z + w, z, w C 6. z z = z 2, z C 7. R(z) z, I(z) z, z C Si z = a + bi, existe u θ R de forma que cos(θ) = a z, si(θ) = b z A u tal θ se le llama u argumeto de z (de hecho, si θ es u argumeto, θ +2kπ, k Z tambié lo es). Si 0 θ < 2π, diremos que θ es el argumeto pricipal de z y lo represetaremos por Arg(z). A cotiuació veremos, gráficamete, la relació etre las partes real e imagiaria de u complejo y su módulo y argumeto, Fig.2. Figura.2: Módulo y argumeto de u úmero complejo. Dado que r = z, etoces cualquier úmero complejo z = a + bi verifica que a = z cos(θ) y b = z si(θ), por lo que se puede represetar tambié 9
21 de la forma z = z (cos(θ) + i si(θ)) represetació que recibe el ombre de expresió trigoométrica de z. La expresió cos(θ) + i si(θ) se suele represetar por e iθ y así el complejo z de módulo z y argumeto θ tambié se puede escribir como z = z e iθ la cual recibe el ombre de expresió polar de z. La vetaja de utilizar esta expresió es que las operacioes co complejos se puede realizar como si se tratara de expoeciales, lo que facilita las operacioes de productos, cocietes y potecias. Si z = r e iα y w = s e iβ, etoces. z w = ( r e iα) (s e iβ) = rs e i(α+β) 2. z = ( r e iα) = r e iα 3. z = z = r e iα 4. z = r e iα Ejemplo.9 Si z = i, etoces θ [0, 2π[ z = 2 + ( ) 2 = 2 / cos(θ) = 2 si(θ) = 2 θ = 7π 4 y etoces, z = ( 2 cos 3π 4 + i si 3π 4 ) = 2 e i 3π 4 Ejercicio.9 Expresa e forma polar los complejos w = y w 2 = i. (Sol.: w = e 0i = y w 2 = e i π 2 ) Ejercicio.0 Expresa e forma polar los úmeros complejos w = i y w = ( 3i). (Sol.: w = 2 e i π 4 y w 2 = 2 e i π 3 ) 0
22 Ejercicio. Expresa e forma polar el complejo w = 4( + i) 4. Ejercicio.2 Expresa e forma polar el complejo w = 2 + 2i. i Ejercicio.3 Calcula + z 2 + z 2, si z C y z =. (Sol.: w = 6 ) (Sol.: w = 2 2 e i π 4 ) (Sol.: 4 ).2.3. Raíces eteras de u úmero complejo Dado el úmero complejo z = r e iθ, o ulo, existe úmeros z k, k = 0,, 2,...,, que verifica (z k ) = z; es decir, existe, justamete, raíces -ésimas de z. Además, estos úmeros se expresa e forma polar como z k = r e i θ+2kπ, k = 0,, 2,..., Estas fórmulas implica que todas las raíces de u úmero complejo tiee el mismo módulo y sus argumetos se obtiee empezado e θ/ e icremetado, sucesivamete, 2π/ radiaes. Ejemplo.0 Calcula las raíces cúbicas de z = 8i. Solució: Observamos primero que z = 8 e 3πi 2. Por tato, segú las fórmulas ateriores, las tres raíces cúbicas de z so para k = 0,, 2. 3 z = 3 8 e i 3π/2+2kπ 3
23 .2.4. Expoecial compleja y Logaritmo complejo Dado u úmero complejo z = x + iy, la expoecial de z se defie Exp(z) = e x (cos(y) + i si(y)). Por otra parte, dado u úmero complejo z = r e iθ, u logaritmo de z es u úmero complejo w tal que e w = z. Se deotará w = log(z) y se verifica que log(z) = l(r) + i(θ + 2kπ); es decir, log(z) es u úmero complejo cuya parte real es el logaritmo eperiao real del módulo de z y cuya parte imagiaria es u argumeto de z. Ejemplo. Calcula log(3 + 3i). Solució: Notemos primero que, expresado el complejo e forma polar, 3 + 3i = 3 2 e i π 4 Por tato, log(3 + 3i) = l(3 2) + i( π 4 + 2kπ) Ejercicio.4 Comprueba que si la forma polar de z = e iθ co α R, etoces, se cumple que z = Exp(iθ)..3. Problemas adicioales Ejercicio.5 Ecuetra todos los valores x R que verifique las siguiete expresioes: (a) x + + x + 2 < 2; (b) x 2 7x + 2 > x 2 7x + 2; (c) x2 5x x + 2 (Sol.: (a) ] 2.5, 0.5[; (b) ]3, 4[; (c) ]0.29, 0.76[ ]5.23, 6.7[ ) 2
24 Ejercicio.6 Demuestra, por iducció, que si r R, r, se verifica para todo N. + r + r r = r+ r Ejercicio.7 Demuestra, por iducció, que para todo N = ( ) 2 Ejercicio.8 Calcula la parte real e imagiaria de los siguietes úmeros complejos: (a) (3 2i)(2 + 3i) ; (b) i 5787 ; (c) ( + 4i) 3. (3 4i) (Sol.: (a) 6/ i/25; (b) i; (c) 47 52i ) Ejercicio.9 Sea z y z 2 dos úmeros complejos distitos tales que r = (z + z 2 )i z z 2 Halla la relació que debe cumplir z y z 2 para que r sea u úmero real. (Sol.: z = z 2 ) Ejercicio.20 Expresa e forma polar los úmeros complejos z = 3 + 3i y z 2 = 4i. (Sol.: z = 3 2 e πi/4 y z 2 = 4 e πi/2. ) Ejercicio.2 Expresa e forma biómica el úmero complejo z = 2e 5πi/4. (Sol.: z = i ) Ejercicio.22 Halla la forma biómica de los siguietes úmeros complejos: 3
25 (a) (4 + 3i) 2 (b) 3+2i 3 2i (c) ( +i 2 ) 4 (d) Exp( i) (e) log( 2 + 2i) (Sol.: (a) i; (b)5/3 + 2i/3; (c) ; (d) i; (e) l(2 2) + (3π/4 + 2kπ)i ) Ejercicio.23 Halla los úmeros complejos z tales que z 6 9z = 0. (Sol.:, e 2πi 3, e 4πi 3, 2, 2 e 2πi 3, 2 e 4πi 3. ) Ejercicio.24 Determiar los úmeros complejos o ulos z tales que su cuadrado es igual a su cojugado. (Sol.:, 2 + i 3 2, 2 i 3 2. ) Ejercicio.25 Demuestra que si z + z de z es ula o z =. es real, etoces la parte imagiaria 4
26 Tema 2 Sucesioes Numéricas Imagiemos la cola de etrada a u espectáculo formada por persoas que ha sido umeradas de la forma habitual; el primero de la cola lleva el úmero, el segudo el úmero 2 y así sucesivamete; pero co la diferecia respecto del mudo real de que la fila es ifiita. Cómo podría saber u espectador que observa la cola que dicha fila es ifiita? Naturalmete, podría respoderse que porque o alcaza co la vista el fial de la cola (que por cierto o existe tal fial); pero podríamos objetar que tal vez es u problema de vista y o de ifiitud; acaso e ua cola de miles de milloes de persoas alcazaríamos a ver el fial? Ua respuesta más adecuada matemáticamete es que e esta fila toda persoa tiee siempre alguie detrás; es decir, siempre existe u sucesor a cualquier persoa que esté haciedo cola. Esto resulta del hecho de que para umerar la cola hemos empleado el cojuto de los úmeros aturales N y ésta es, precísamete, ua de sus características eseciales. Acabamos de formar ua sucesió (de persoas). Ituitivamete hablado, pues, ua sucesió es ua lista ifiita de objetos que está umerados (ordeados) siguiedo el orde de los úmeros aturales,, 2,.... Así al primer térmio de la sucesió le correspode el ídice (úmero e la cola) ; el siguiete lleva el ídice 2 y así sucesivamete. Cabe decir que, e ocasioes, será coveiete empezar co el ídice 0 e vez de co. E este tema, se tratará las sucesioes uméricas; es decir aquellas listas cuyos objetos umerados so, a su vez, úmeros. Auque el título hace 5
27 referecia a sucesioes uméricas e geeral; es decir, reales y complejas, os limitaremos a estudiar las sucesioes reales, ya que el estudio de las sucesioes complejas se reduce a áquel mediate el aálisis de las partes reales y complejas de los respectivos térmios. 2.. Sucesioes reales. Subsucesioes Defiició 2. Ua sucesió de úmeros reales es ua aplicació a : N R El rago de esta aplicació es el cojuto (ordeado) {a(0), a(), a(2), a(3),..., a(),...} y deotado a = a() lo podemos represetar abreviadamete como {a } + =0. Tambié se utiliza la otació {a } para represetar a ua sucesió, sobretodo si o os importa señalar desde que térmio empezamos. E geeral, las sucesioes puede empezar desde u atural 0 > 0, pero e las disquisicioes teóricas etedemos que empieza desde =. Por tato, ua forma de escribir ua sucesió es dado la fórmula del térmio geeral a. Ejemplo 2. {, 2, 3,...}; es decir, a =,. {,,,,,,...} es decir, a = ( ) +,. {, 2, 4, 8...}; es decir, a = 2, 0. Si embargo, e alguos casos la sucesió se defie o bie por compresió o bie por recurrecia; esta última sigifica que el térmio geeral a se defie e fució de uo o varios térmios ateriores. 6
28 Ejemplo 2.2 La sucesió formada por la uidad y los úmeros primos. No es posible escribir a e fució de : {, 3, 5, 7,, 3, 7, 9,...}. a 0 = ; a = ; a = a + a 2 para 2; que da la coocida sucesió de Fiboacci dode cada térmio es la suma de los dos ateriores: {,, 2, 3, 5, 8, 3...} Ua forma de represetar gráficamete las sucesioes reales es como fucioes, es decir, como pares ordeados (, a ), lo que puede ser útil e ocasioes para el estudio de sus propiedades. E el eje de abcisas se represeta los úmeros aturales y e el eje de ordeadas los valores reales a. Dado que la variable sólo admite valores aturales, la represetació gráfica se visualizará, etoces, como u cojuto de putos aislados, Fig 2. Figura 2.: Represetació gráfica de ua sucesió Defiició 2.2 Ua subsucesió de úmeros aturales es ua aplicació estrictamete creciete: N N j j es decir que se cumple < 2 < 3 <... < p < p+ <... 7
29 Esto permite defiir, dada ua sucesió {a } de úmeros reales, ua subsucesió de {a } como la aplicació N N j j a R a j Es decir, dode los uevos ídices j forma ua subsucesió de N. Por tato, la subsucesió, que deotaremos por {a j } + j=, puede etederse como u subcojuto ifiito (y ordeado) de {a }. Ejemplo 2.3 Dada ua sucesió cualquiera {a } so subsucesioes: {a 2 }, la subsucesió de los térmios de orde par; {a 2+ }, la subsucesió de los térmios de orde impar; {a 2 }, la subsucesió de los térmios de orde potecias de 2; {a +3 }, la subsucesió formada desechado los tres primeros térmios. Ejemplo 2.4 Cosidera la sucesió {, 2, 3,,...}. Etoces, 4 { 2, 4, 6,..., 2,...} es subsucesió, co = 2, 2 = 4, 3 = 6,... { 2, 4, 8,..., 2,...} es subsucesió, co = 2, 2 = 4, 3 = 8,.... { 3, 2, 5,,...} o es subsucesió. (No respeta el orde) 4 {0, 2, 4,...} o es subsucesió. (No es subcojuto) Sucesioes moótoas Al observar la sucesió { } cuyos térmios escribimos a cotiuació, 2, 3, 4, 5, 6, 7, 8,... 8
30 vemos como cada térmio es mayor que su sucesor; es decir que la sucesió decrece; Fig Figura 2.2: Sucesió decreciete Por el cotrario, la sucesió {}, 2, 3, 4, 5,... cumple que cada térmio es meor que su sucesor; es decir, la sucesió crece; Fig Figura 2.3: Sucesió creciete Formalizamos estos coceptos e la siguiete defiició. 9
31 Defiició 2.3 Diremos que {a } es : moótoa creciete si, y sólo si, a a +, moótoa decreciete si, y sólo si, a a +, N N moótoa cuado es creciete o decreciete. Cuado las desigualdades so estrictas se dirá que las sucesioes so estrictamete crecietes o estrictamete decrecietes, segú el caso. Ejemplo 2.5 Si cosideramos de uevo las sucesioes ateriores {} es creciete, porque +, para todo { } es decreciete, porque, para todo + E ocasioes el estudio de la mootoía o es ta evidete y requiere realizar alguas operacioes. Ejemplo 2.6 Determia si la sucesió { 2 } es moótoa. 2 Solució: Primero calculamos alguos de los primeros térmios para determiar si es moótoa y e qué setido. Para o complicar la otació asumimos que el primer térmio será deotado por a 2 (e vez de por a ): por lo que, a 2 = 4 7 ; a 3 = 2 26 ; a 4 = 9 63 a 2 > a 3 > a 4 lo cual parece idicar que es moótoa decreciete. Para probarlo, debemos verificar que a > a +. Si escribimos esta codició > ( + )2 + 3 ( + ) 3 20
32 y ahora, se trata de desarrollar esta expresió hasta llegar a ua codició que sea cierta. Empezamos por quitar deomiadores (ambos so positivos por lo que la desigualdad permaece) ( 2 + 3)(( + ) 3 ) > (( + ) 2 + 3)( 3 ) y, desarrollado los parétesis, ( ) > que equivale a > 0 lo cual es cierto para cualquier valor de al ser todos los sumados positivos. Queda así comprobado que a > a +, para todo, por lo que la sucesió resulta ser moótoa decreciete. Ejemplo 2.7 Determia si la sucesió { }! 2 es moótoa. Solució: Primero calculamos alguos de los primeros térmios para determiar si es moótoa y e qué setido: por lo que, a = 2 ; a 2 = 2 4 ; a 3 = 6 8 ; a 4 = 24 6 ; a a 2 < a 3 < a 4 y parece idicar que es moótoa creciete. Para probarlo, debemos verificar que a < a +, para todo. Dado que todos los térmios so positivos y que ivolucra factoriales y potecias vamos a probar que a + a > ( + )! =, para todo! 2 2 Queda así comprobado que a < a +, para todo, por lo que la sucesió resulta ser moótoa creciete. 2
33 Ejercicio 2. Estudia la mootoía de la sucesió a = ,. (Sol.: {a } es moótoa creciete ) Ejercicio 2.2 Estudia la mootoía de la sucesió a = ,. (Sol.: {a } es moótoa decreciete ) (2 )!! Ejercicio 2.3 Estudia la mootoía de la sucesió a =! 2, (H: (2 )!! = (2 ) (2 3) 3 ; es decir, es el producto de todos los impares meores o iguales a 2 ). (Sol.: {a } es moótoa decreciete ) 2.3. Sucesioes acotadas Defiició 2.4 Sea {a } ua sucesió real y M R. Si a M, N diremos que {a } está acotada superiormete. E este caso el úmero M se llama cota superior. Si a M, N diremos que {a } está acotada iferiormete. E este caso el úmero M se llama cota iferior. Diremos que {a } está acotada si lo está superior e iferiormete. Esto equivale a decir que a M, N Gráficamete, ua sucesió acotada es, pues, aquella cuyos térmios se ecuetra situados e ua bada horizotal de achura 2M, como puede observarse e la Fig
34 Figura 2.4: Sucesió acotada a M Ejemplo 2.8 Veamos alguos ejemplos de sucesioes acotadas. { } está acotada porque, N {( ) + } está acotada porque ( ) +, N {} o está acotada superiormete. {l ( ) } o está acotada iferiormete (se verá más adelate que lím l(/) = ). { 2 } + 3 Ejemplo 2.9 Determia si la sucesió 3 está acotada. 2 Solució: Puesto que los térmios de la sucesió siempre so positivos, queda claro que está acotada iferiormete por 0; es decir, , 2 Para acotarla superiormete, se utiliza u pequeño artificio: aumetar el grado del umerador para que coicida co el del deomiador y poder realizar la divisió = = 2 23
35 { } Ejercicio 2.4 Determia si la sucesió está acotada. + N (Sol.: 0 < + < ) Ejercicio 2.5 Determia si la sucesió (Sol.: { 4 } está acotada. 2 y o acotada superiormete ) 2.4. Sucesioes covergetes Observamos de uevo la sucesió { }+ =, escribiedo alguos de sus térmios:, 2, 3, 4, 5, 6, 7, 8,... Cuato más avazamos, más pequeño es el térmio correspodiete. Parece que la sucesió va acercádose a cero y, por tato, se dice que tiee límite cero. Por cotra e la sucesió {} pasa lo cotrario:, 2, 3, 4, 5,... cuato más avazamos más grade se hace el térmio correspodiete y, etoces, se dice que tiee límite +. Fialmete, si tomamos la sucesió:, 0,, 0,, 0,... se observa que por mucho que avacemos la sucesió siempre oscila etre 0 y y se dice que es oscilate. Estos coceptos se formaliza a cotiuació e las siguietes defiicioes. Defiició 2.5 Diremos que {a } es covergete y tiee límite λ R sii y lo escribiremos ɛ > 0 0 N / si 0 a λ < ɛ lím a = λ. Si ua sucesió o es covergete, etoces se dice que es divergete; pero distiguiremos alguos tipos de divergecia. 24
36 Diremos que {a } es divergete y tiee límite + sii y lo escribiremos K > 0 0 N / si 0 a > K lím a = +. Diremos que {a } es divergete y tiee límite sii y lo escribiremos K < 0 0 N / si 0 a < K lím a =. Diremos que {a } es divergete y tiee límite sii y lo escribiremos K > 0 0 N / si 0 a > K lím a =. Diremos que {a } es oscilate si o es covergete i divergete a ± o Nota: E realidad, ua sucesió {a } tiee límite si la sucesió de los valores absolutos { a } tiee límite +. Por eso, toda sucesió divergete a + o, tambié tiee límite, pero el recíproco o es cierto (véase el Ejemplo 2.0). Ejemplo 2.0 Veamos alguos ejemplos de sucesioes covergetes y divergetes.. { } es covergete y lím = 0 2. {} es divergete y lím = + 3. { } es divergete y lím ( ) = 4. {,, 2, 2,..., ( ) +,...} es divergete y lím ( ) + = 5. {, 2,, 2,, 2,, 2,...} es oscilate (y acotada) 6. {, 2,, 3,, 4,, 5,...} es oscilate (y o acotada) 7. {si } es oscilate (y acotada) 25
37 Gráficamete el cocepto de límite se iterpreta como que la cola de la sucesió se aproxima a ua recta horizotal de ecuació y = L, si lím a = L; Fig. 2.5, Figura 2.5: Sucesió covergete o por el cotrario, la cola supera cualquier cota K si lím a = + ; Fig Figura 2.6: Sucesió divergete E el siguiete teorema se resume alguas propiedades básicas de los límites. 26
38 Teorema 2.6 Sea {a } ua sucesió covergete. Etoces,. El límite es úico. 2. La sucesió es acotada. 3. Cualquier subsucesió es covergete y tiee el mismo límite. 4. lím a = λ lím(a λ) = 0 lím a λ = 0 Por otra parte, si la sucesió {a } es divergete a ± etoces cualquier subsucesió es divergete y tiee el mismo límite. La propiedad (2) aterior proporcioa u método para determiar si ua sucesió está acotada; es decir, las sucesioes co límite fiito está acotadas; auque el recíproco o es cierto, e geeral: la sucesió oscilate {, 0,, 0,...} está acotada pero o tiee límite. La propiedad (3) aterior permite elimiar u úmero fiito de térmios al calcular el límite de ua sucesió. E particular, el límite o depede de los primeros térmios sio de la cola de la sucesió; lo cual ya estaba implícito e la defiició de límite. Teorema 2.7 La relació de los límites co el orde de los úmeros reales es la siguiete:. Si a b, para todo 0 y existe lím a y lím b, etoces lím a lím b 2. Si lím a = λ < α, etoces existe 0 tal que a < α, para cada 0 3. Si lím a = λ > α, etoces existe 0 tal que a > α, para cada 0 E particular, si lím a 0, la sucesió {a } tiee el mismo sigo que su límite excepto, como mucho, e u úmero fiito de térmios. 27
39 Ya vimos que toda sucesió co límite fiito está acotada y que el recíproco o es cierto e geeral. Si añadimos ua codició de mootoía obteemos dicho recíproco Teorema 2.8 La relació etre la covergecia y la mootoía se resume e las siguietes propiedades.. Si {a } es creciete y acotada superiormete, etoces {a } es covergete. 2. Si {a } es decreciete y acotada iferiormete, etoces {a } es covergete. 3. Si {a } es creciete y o acotada superiormete, etoces {a } es divergete a Si {a } es decreciete y o acotada iferiormete, etoces {a } es divergete a. Teorema 2.9 (Aritmética de sucesioes covergetes) Sea {a } y {b } dos sucesioes covergetes. Etoces,. lím (a + b ) = lím a + lím b 2. lím (α a ) = α lím a 3. lím (a b ) = lím a lím b a lím a 4. lím = si lím b 0 b lím b 5. lím (a ) b = (lím a ) lím b si lím a > 0 Para coocer el valor del límite cuado ua o las dos sucesioes ateriores tiee límite ifiito, se aplica la llamada aritmética ifiita que se resume e la tabla siguiete. E lo que sigue debe etederse que a R represeta el límite de ua sucesió {a } y ± el de ua sucesió {b }. 28
40 Suma: (+ ) + (+ ) = + ( ) + ( ) = a + (+ ) = + a + ( ) = Producto: a(+ ) = { + si a > 0 si a < 0 a( ) = { si a > 0 + si a < 0 (+ )(+ ) = + ( )( ) = + (+ )( ) = Cociete: + a = + si a > 0 si a < 0 si a = 0 a = si a > 0 + si a < 0 si a = 0 a + = 0 a = 0 a =, si a 0 0 Potecias: a + = { + si a > 0 si 0 a < a = { 0 si a > + si 0 a < (+ ) + = + (+ ) = 0 (+ ) a = { + si a > 0 0 si a < 0 29
41 2.5. Cálculo de límites Co la aritmética ifiita, puede presetarse los siguietes tipos de idetermiacioes:, 0 0,, 0,, 0, 0 0 Veamos cómo resolver alguas de ellas: Ejemplo 2. Calcula el límite lím. + 2 Solució: E este caso, se tiee u cociete de poliomios y ambos tiede a + por lo que, e pricipio, estamos ate ua idetermiació del tipo. El procedimieto a seguir es dividir umerador y deomiador por la potecia de mayor grado; e este caso, 2. lím = lím = 0 = basta observar, e este último paso, que los cocietes y 2 a 0. tiede ambos Si se quiere determiar el sigo del, auque ello o es siempre posible, basta determiar el sigo de la sucesió cuado es grade. E este caso, para valores grades de la sucesió es siempre positiva, por lo que puede afirmarse que el límite es +. Ejemplo 2.2 Calcula el límite lím Solució: E este caso, se tiee u cociete dode umerador y deomiador tiede a, por lo que, e pricipio, estamos ate ua idetermiació del tipo. El procedimieto a seguir es dividir umerador y deomiador por la potecia de mayor grado; e este caso, (auque el umerador o 30
42 es u poliomio, se asimila a éste para el cálculo de límites, tomado como potecia de mayor grado 2 = ). lím = lím = 3 = Ejercicio 2.6 Calcula lím. + 2 (Sol.: ) Ejercicio 2.7 Calcula lím (Sol.: 2 ) Ejercicio 2.8 Calcula lím (Sol.: ) Ejercicio 2.9 Calcula lím (Sol.: 0 ) 2 k + 3 k Ejercicio 2.0 Calcula lím k + 3 k 2 (H: Divide umerador y deomiador por la mayor + 2k+3 potecia). Ejemplo 2.3 Calcula el límite lím ( ) (Sol.: 3 ) Solució: E este caso, se tiee ua diferecia de sucesioes dode ambas tiede a +, por lo que, e pricipio, estamos ate ua idetermiació del tipo. Dado que puede verse como ua diferecia de raíces cuadradas 3
43 ( = 2 ), el procedimieto a seguir es multiplicar y dividir por la expresió cojugada: lím ( ) 2 ( = lím )( ) = lím = lím = 2 2 = ya que e este último paso, volvemos a teer u cociete de poliomios que ya debemos saber resolver. Ejercicio 2. Calcula lím ( ) (Sol.: ) Ejercicio 2.2 Calcula lím (Sol.: 2 ) ( 4 Ejercicio 2.3 Calcula lím ) (H: Aplica dos veces la operació de multiplicar y dividir por el cojugado). (Sol.: 0 ) A cotiuació se expoe alguos métodos más para resolver éstas y otras idetermiacioes: (a) tipo ( ): se aplica la fórmula de Euler. } a = lím a b b lím b(a ) = e ( 2 ) + 3 Ejemplo 2.4 Calcula el límite lím
44 Solució: E este caso, se tiee ua potecia de sucesioes dode la base tiee límite (debería ser claro ya) y el expoete tiee límite, por lo que, estamos ate ua idetermiació del tipo. El procedimieto cosiste e aplicar la fórmula de Euler: ( ( 2 ) 2 ) + 3 lím 2 = e lím ( 2 = e lím ) = e lím = e ( 2 ) Ejercicio 2.4 Calcula lím ( 3 Ejercicio 2.5 Calcula lím 2 ) ( 2 ) Ejercicio 2.6 Calcula lím 2 2. Ejercicio 2.7 Calcula lím ( + ) +. (Sol.: e 7 ) (Sol.: e 2/3 ) (Sol.: 0 ) (Sol.: ) (b) tipo ( ): se aplica el criterio de Stolz. = b + (b ) creciete b > 0, lím a b = lím a + a b + b 33
45 Ejemplo 2.5 Calcula el límite lím Solució: E este caso, se observa que el umerador es ua sucesió formada por ua suma cuyo úmero de sumados varía co el valor de. Se aplica el criterio de Stolz, llamado a a la sucesió del umerador y b a la del deomiador: lím a b = lím a + a b + b = lím ( + ) ( ) ( + ) 2 2 = lím = 2 Ejercicio 2.8 Calcula lím (Sol.: ) Ejercicio 2.9 Calcula lím (Sol.: 9 2 ) Ejercicio 2.20 Calcula lím log(!) log (Sol.: ) a + 2a 2 + 3a a Ejercicio 2.2 Calcula lím 2, sabiedo que a es ua sucesió covergete co límite lím a = a. (Sol.: a 2 ) (c) tipos ( 0 ) y (0 0 ): se aplica el criterio de Stolz para la raíz. b + (b ) creciete = lím b a = lím b + b b > 0, a+ a 34
46 Ejemplo 2.6 Calcula el límite lím!. Solució: E este caso, se aplica el criterio de Stolz para la raíz. Llamado a a la sucesió del radicado y b a la del radical: lím a+ b b + ( + )!/( + ) a = lím + b = lím ( + ) a!/ ( + ) = lím ( + ) ( + ) = lím ( ) ( + ) ) = lím = e + Ejercicio 2.22 Calcula lím. (Sol.: ) Ejercicio 2.23 Calcula lím (Sol.: ) ( Ejercicio 2.24 Calcula lím + ). (Sol.: 0 ) Ejercicio 2.25 Calcula lím (Sol.: ) (d) tipos ( ) y ( 0 0 ): cambiamos a límite de fucioes para poder aplicarle la regla de L Hopital: Se busca dos fucioes reales f y g, cotiuas y derivables de forma que f() = a y g() = b ; etoces, a lím = + b f(x) lím x + g(x) = Ejemplo 2.7 Calcula el límite lím e. 35 lím f (x) x + g (x)
47 Solució: El límite propuesto es ua idetermiació del tipo. E este caso, puesto que ambas sucesioes o tiee relació, lo más secillo es tomar las fucioes f(x) = e x y g(x) = x y aplicar la regla de L Hopital: lím f(x) g(x) = lím f (x) g (x) = lím e x = + por lo que, lím e = +. Ejercicio 2.26 Calcula el límite lím l(). (Sol.: 0 ) 2.6. Ifiitésimos Defiició 2.0 Ua sucesió {a } se dice u ifiitésimo si lím a = 0 Dos ifiitésimos {a } y {b } se dice equivaletes si a lím = b Las propiedades más usuales de los ifiitésimos se resume e los dos resultados siguietes. Teorema 2. Si {a } es u ifiitésimo y {b } es ua sucesió acotada, etoces lím a b = 0 es decir, {a b } es u ifiitésimo. Teorema 2.2 Sea {a } y {b } dos ifiitésimos equivaletes y {c } ua sucesió cualquiera. Etoces,. lím a c = lím b c 36
48 c c 2. lím = lím a b Esta última propiedad os dice que e el cálculo de límites podemos substituir u ifiitésimo por u equivalete (siempre y cuado aparezca como productos o cocietes). Por tato, resulta coveiete coocer alguos ifiitésimos equivaletes. Los más usuales so: Ifiitésimos Equivaletes. Si {a } es u ifiitésimo, etoces {log( + a )} {a } {si(a )} {a } {ta(a )} {a } {arcta(a )} {a } { cos(a )} { a2 2 } {b a } {a log b} Ejemplo 2.8 Vamos a calcular lím log( ). Solució: Aplicamos que, segú la tabla aterior, { log ( + 2 )} { } y, etoces, el Teorema 2.2 os permite escribir lím log( ) = lím 2 2 = lím 2 = 0 arcta(log( 2 + Ejercicio 2.27 Calcula el límite lím )). ta( ) (Sol.: ) 37
49 Ejercicio 2.28 Calcula el límite lím ( a ), a > 0. Ejercicio 2.29 Calcula el límite lím ( (Sol.: l(a) ) ) a + b, a, b > 0. 2 Ejercicio 2.30 Calcula el límite lím ta(a + B) = ta(a) + ta(b) ta(a) ta(b) ). ta(a + b ) ta a (Sol.: ab ) (H: Recuerda que (Sol.: e 2b si(2a) ) 2.7. Ifiitos Defiició 2.3 Ua sucesió {a } se dice u ifiito si lím a = (± ) Dos ifiitos {a } y {b } se dice equivaletes si a lím = b Diremos que {a } es de mayor orde que {b } si a lím = + b Teorema 2.4 Si {a } es u ifiito y {b } es ua sucesió acotada, etoces lím (a + b ) = es decir, {a + b } es u ifiito. El cocepto de ifiito de mayor orde se utiliza a meudo e la resolució de límites idetermiados del tipo. Por otra parte, los ifiitos equivaletes se utiliza segú la propiedad siguiete. 38
50 Teorema 2.5 Sea {a } y {b } dos ifiitos equivaletes y {c } ua sucesió cualquiera. Etoces,. lím a c = lím b c c c 2. lím = lím a b Esta propiedad os dice que e el cálculo de límites podemos substituir u ifiito por u equivalete (siempre y cuado aparezca como productos o cocietes). Ifiitos Equivaletes! e 2π (Fórmula de Stirlig) Ejemplo 2.9 Calculad lím 3 3 (!) 3 (3 + )!. Teiedo e cueta la fórmula de Stirlig sabemos que por lo que tambié, y así, lím 3 3 (!) 3 (3 + )! = lím! e 2π (3 + )! (3 + ) 3+ e (3+) 2π(3 + ) 3 3 ( e 2π) 3 (3 + ) 3+ e (3+) 2π(3 + ) e 3 ( 2π) 3 = lím (3 + ) 3 (3 + ) e 3 e 2π(3 + ) ( ) 3 3 2π 2π = lím e 3 + (3 + ) 2π(3 + ) ( ) 3 3 y como, lím = e, 3 + = lím 2π 2π (3 + ) 2π(3 + ) = 2π
51 2.8. Problemas adicioales Ejercicio 2.3 (a) Demuestra que la suma de ua sucesió covergete y ua divergete es divergete (H: Supó que la suma fuera covergete y aplica la Propiedad 2.9 para llegar a ua cotradicció). (b) Aplica lo aterior para estudiar el carácter de la sucesió ( a = + ) ( + ( ) 3 ), =, 2,... (Sol.: (b) Divergete (oscilate). ) Ejercicio 2.32 Demuestra que la sucesió defiida por recurrecia a = es covergete y calcula su límite. a + = 2 + a, (H: Demuestra que la sucesió es moótoa creciete y acotada superiormete (Propiedad 2.8). Para el cálculo del valor del límite, toma límites e la relació de recurrecia) (Sol.: {a } es creciete y acotada superiormete; y lím a = 2. ) Ejercicio 2.33 Ídem co a = a + = 2a + 3, (Sol.: {a } es creciete y acotada superiormete; y lím a = 3. ) Ejercicio 2.34 Ecuetra la relació etre a y b para que se verifique lím ( + a + ) 2+3 = lím ( ) + 3 b (Sol.: b = 2(a ) ) 40
52 Ejercicio 2.35 Calcula los siguietes límites si 2 ( (a) lím 2 ) log( + ) ( + 2) 5 cos( π. 4 ) (b) lím ( + + ). (Sol.: (a) 2; (b) e ) Ejercicio 2.36 Calcula + 2! + 3 3! ! lím + 2. (Sol.: e /2 ) Ejercicio 2.37 Calcula el límite: lím ( ) (H: Calcula el logaritmo del límite) (Sol.: 2 ) Ejercicio 2.38 Calcula el límite de las siguietes sucesioes: (a) {a } = (b) {b } = { (log ) } α log (α > 0, β > 0) log β = { } = (Sol.: (a) α ; (b) 2. ) β Ejercicio 2.39 Calcula lím 2 2 (!) 2 (2 + )!. (Sol.: 0 ) 4
53 Ejercicio 2.40 Sea {a } = y {b } = dos sucesioes de úmeros reales a positivos de maera que lím =. b Explica razoadamete si las siguietes afirmacioes so ciertas o o: (a) (b) a 2 lím b 2 a lím b = = (c) log a lím = log b Si algua afirmació o es cierta basta dar u cotraejemplo. (Sol.: a) Cierta; (b) Falsa; (c) Falsa. ) 42
54 Tema 3 Series Numéricas Imagiemos que se va a celebrar ua carrera co las siguietes reglas:. El primer miuto debe recorrerse 00 metros. 2. El miuto siguiete debe recorrerse la mitad, 50 metros. 3. El miuto siguiete debe recorrerse la mitad del aterior, 25 metros. 4. El miuto siguiete dee recorrerse la mitad del aterior, 2,50 metros. y así sucesivamete. Por otra parte, al mismo tiempo empieza otra carrera, co las reglas ligeramete modificadas:. El primer miuto se recorre 00 metros. 2. El miuto siguiete se recorre la mitad de 00 metros, 50 metros. 3. El miuto siguiete se recorre la tercera parte de 00 metros, 33,3 metros. 4. El miuto siguiete se recorre la cuarta parte de 00 metros, 25 metros. y así sucesivamete. 43
55 Dos corredores empieza a la vez las carreras. Si la meta de la primera se ecuetra situada a 300 metros y la de la seguda a 000 metros, quié llega primero a la meta y cuáto tiempo tarda? Llamamos D = 00 metros la distacia recorrida e el primer miuto. La primera carrera va recorriedo las distacias: D + D 2 + D 4 + D La seguda carrera va recorriedo las distacias: D + D 2 + D 3 + D La preguta es cuál de estas sumas alcaza la distacia a la que está situada la meta respectiva. Al acabar este tema deberemos ser capaces de dar ua respuesta razoada. 3.. Series reales Del mismo modo que e el capítulo aterior, os limitaremos a tratar co series de úmeros reales, porque, de uevo, el estudio de las series complejas se reduce al estudio de las series determiadas por las partes reales e imagiarias. Cosideramos ua sucesió de úmeros reales {a, a 2, a 3,..., a,...} defiida de la si- A partir de ella formamos ua ueva sucesió {S } = guiete forma: S = a S 2 = a + a 2 S 3 = a + a 2 + a 3. S = a + a 2 + a a = La respuesta es que el primer corredor o cosigue llegar jamás a la meta mietras el segudo sí. 44 k= a k
56 La sucesió {S } así defiida se llama sucesió de las sumas parciales y a recibe el ombre de térmio geeral -ésimo. Llamaremos serie al par de sucesioes {(a ), (S )}. Defiició 3. Diremos que la serie {(a ), (S )} es covergete si existe lím S = S R. Al valor S se le llama suma de la serie y lo escribiremos S = lím a = a k= = Por abuso de otació represetaremos a la serie {(a ), (S )} por su suma, es decir, por = a ; auque es posible que dicha suma i siquiera exista. Notas: Alguas observacioes a teer e cueta: El ídice de sumació es ua variable muda, y puede sustituirse por cualquier otra letra. No es ecesario que ua serie empiece a sumar desde =. Puede empezar desde = 0 o = p (p > ); pero siempre se puede reescribir para que empiece e = mediate u cambio de variable (ver el Ejemplo 3.25). S siempre represeta la suma de los primeros térmios de la sucesió a y etoces se deberá teer cuidado al calcularla cuado la serie o empiece por =. Las defiicioes de covergecia y divergecia o depede del térmio a partir del cual empieza a sumar, auque si afecta al valor de la suma (véase el Teorema 3.3). Así, las propiedades que o ivolucre a la suma de la serie so ciertas idepedietemete del térmio e que empiece. Por este motivo, y por comodidad, euciaremos casi todas las propiedades para series que empiece e = e, icluso, a veces i ta siquiera especificaremos desde qué térmio empieza a sumar, escribiedo úicamete a. Auque hablemos de la suma de ua serie, o debemos olvidar que dicha suma es, e realidad, u límite de sumas y, etoces, puede o 45
57 ser ciertas las propiedades usuales de las sumas fiitas: por ejemplo, el orde de los sumados sí puede alterar la suma (cosultad la Secció 3.3); o tambié resulta ser falsa la propiedad asociativa (ver el Ejemplo 3.6). Ejemplo 3. Reescribe la serie empiece e =. =2 2 para que el ídice de sumació Solució: Se trata, simplemete, de realizar u pequeño cambio de variable. =2 2 = + = + 2 = 2 k= dode k = y, substituyedo = k +, = k= reombrado el cotador. + (k + ) 2 = ( + ) 2 = Observa que la serie o ha cambiado; sólo se ha modificado el cotador: =2 2 = = ( + ) 2 = Ejercicio 3. Reescribe la serie a sumar desde = : (Sol.: =3 para que empiece log() log [(log())] = ( + 2) log( + 2) log [(log( + 2))] ) 46
58 ) para que empiece a sumar des- Ejercicio 3.2 Reescribe la serie ( =p p de = : (Sol.: = ( + p p ) ) U ejemplo importate lo costituye las llamadas series geométricas. Ejemplo 3.2 Cosideremos la progresió geométrica, r, r 2, r 3,..., r,... de la cual obteemos la serie + r + r r +... = =0 r (r R ) Vamos a calcular S e fució de. Para ello, multiplicamos S por la razó r S = + r + r 2 + r r 2 + r rs = r + r 2 + r 3 + r r + r y restado las dos expresioes S rs = r S = r r si r Para calcular el límite de S distiguimos dos posibilidades, segú el valor de la razó r: r < lím r = 0 lím S = r r > lím r = lím S = Ahora, r = =0 S = S 2 = + = 2. S = lím S = 47
59 r = =0 ( ) S = S 2 = = 0 S 3 = + = S 4 = + = 0. S 2 = S 2 = 0 lím S E defiitiva, la serie geométrica caso, suma exactamete =0 =0 r es covergete sii r < y, e ese r = r Ejemplo 3.3 Calcula la suma de la serie =0 ( 2). Solució: Se trata de ua serie geométrica de razó r =. Etoces, por 2 lo visto e el ejemplo aterior, es covergete (porque r < ) y suma =0 ( 2) = ( 2) = 2 3 Ejercicio 3.3 Calcula la suma de la serie + 0, + 0,0 + 0, (Sol.: 0 9 ) Teorema 3.2 Si teemos dos series covergetes etoces, = a = S y = b = S. (a + b ) = a + = = = b = S + S 48
60 2. (λa ) = λ = = a = λs λ R Ejercicio 3.4 Ecuetra dos series divergetes a y b de maera que la serie suma (a + b ) sea covergete. (Sol.: a = y b = + ) Ejercicio 3.5 Demuestra que si a es covergete y b es divergete etoces (a + b ) es divergete. (H: Si (a + b ) fuera covergete tambié lo sería (a + b a ). Esta propiedad os permite ecotrar la fórmula de la suma de ua serie geométrica cuyo primer térmio o es ; es decir, que o empieza a sumar desde = 0. Ejemplo 3.4 Sea la serie Etoces, =p r = =p =p r = r p + r p+ + r p r p r p = r p r p = r p r k = =p k=0 rp r por lo que, =p r = rp r Ejemplo 3.5 Calcula la suma de la serie = = Solució: La serie puede descompoerse e suma de dos, de la siguiete forma: ( ) 2 (( ) 0 = ( ) ) 0 = = = = ( ) ( ) = = 49
61 puesto que cada ua de estas dos últimas series es covergete ya que se trata de series geométricas de razó r = 5 < y r = 2 <, respectivamete. Por el ejemplo aterior podemos calcular su suma: = por lo que, fialmete, ( ) = /5 5 /5 = + 4 y ( ) = /2 2 /2 = = = = 4 + = 5 4 Ejercicio 3.6 Calcula la suma de la serie =3 ( ) 2 Ejercicio 3.7 Calcula la suma de la serie Ejercicio 3.8 Calcula la suma de la serie (Sol.: 4 ) (Sol.: 32 ) (Sol.: 8 3 ) Teorema 3.3 La covergecia de ua serie o depede del térmio e el que se empiece a sumar; es decir; a = es covergete a =p es covergete Además, e este caso a = (a + a a p ) + = =p a (p > ) 50
62 Teorema 3.4 Si la serie a es covergete etoces tambié lo es dode = b = a + a a b 2 = a + + a a 2 b 3 = a a a 3... b Es decir, tambié es covergete la serie obteida por agrupació de térmios de la primera. La misma propiedad es cierta si cambiamos covergete por divergete a ±. = El recíproco de la propiedad aterior o es cierto como lo prueba el siguiete ejemplo: Ejemplo 3.6 Cosideremos la serie geométrica de razó r =, es decir, Hemos visto ates que esta serie o es covergete, o obstate esto, al agrupar térmios: ( ) + ( ) + ( ) +... = = 0 si resulta ua serie covergete. No obstate, puede probarse que el recíproco de la propiedad aterior sí es cierto si la serie es de térmios positivos Criterios de covergecia Las series geométricas so secillas de sumar. E geeral, calcular la suma exacta de ua serie o resulta tarea fácil. Ates de itetar ecotrar la suma de ua serie puede ser muy útil saber si la serie es o o es covergete. Este tipo de problemas se cooce como Problemas sobre el carácter de ua serie. E las siguietes seccioes estableceremos ua relació de criterios que os permitirá determiar el carácter de ua serie. El primero de todos os da ua codició ecesaria que debe cumplir toda serie covergete. 5
63 Teorema 3.5 (Codició ecesaria de covergecia) Si la serie es covergete lím a = 0 Ejemplo 3.7 La codició aterior o es suficiete, como lo prueba la llamada serie armóica + =. Esta serie verifica que lím = 0 y, o obstate, la serie es divergete. Vamos a probar esto último. Sea {S } la sucesió de las sumas parciales, es decir, = a Así, S = S 2 = S 2 S = térmios > térmios = 2 = 2 de dode lím (S 2 S ) 2 y etoces lím (S 2 S ) 0. Cocluimos, etoces, que la sucesió {S } o puede ser covergete; porque si lím S = S, etoces tambié lím S 2 = S (al ser S 2 ua subsucesió de S ); pero etoces lím (S 2 S ) = 0 y hemos probado ateriormete que o puede ser así. Por tato, la serie armóica es divergete. Ejemplo 3.8 La serie =0 + es divergete porque lím Ejercicio 3.9 Estudia el carácter de la serie = ( 2 + ). + = 0. (Sol.: Divergete. ) 52
64 Ejercicio 3.0 Estudia el carácter de la serie log (2 + 3 ) 2. Ejercicio 3. Estudia el carácter de la serie = = (Sol.: Divergete. ) ( ). + (Sol.: Divergete. ) Series de térmios positivos Ua serie = E este caso, como a dode cada a > 0 se dice ua serie de térmios positivos. S + = S + a + > S resulta que la sucesió de sumas parciales {S } es creciete. Etoces, la serie será covergete si, y sólo si, la sucesió {S } está acotada superiormete. Si o lo está, la serie será divergete a + (Teorema2.8). Ejemplo 3.9 Hemos visto ates que la serie armóica era divergete. Como es de térmios positivos podemos afirmar que su suma vale +. Si ua serie = a es de térmios egativos (i.e., a < 0 ) etoces el estudio de este tipo de series se puede reducir al de las series de térmios positivos, teiedo e cueta que = a = a y esta última ya es de térmios positivos y tiee el mismo carácter. Además, como el carácter de ua serie o se altera si elimiamos u úmero fiito de térmios, equipararemos a este tipo todas aquellas series que si bie o so de térmios positivos, sólo tiee u úmero fiito de térmios egativos. Vamos a ver alguos criterios para averiguar si ua serie de térmios positivos es covergete o divergete. 53 =
65 Teorema 3.6 (Criterio de la serie mayorate) Sea a y b dos series de térmios positivos. Si b es covergete y a b a es covergete Si a es divergete y a b b es divergete Ejemplo 3.0 Sea la serie =2 =2 log Solució: Como log <, 2, resulta <, 2 y como la log + serie es divergete cocluimos que es divergete. log =2 Ejercicio 3.2 Averigua el carácter de la serie Ejercicio 3.3 Sea a y = =2 2 cos(). (Sol.: Divergete. ) b dos series covergetes de térmios = positivos. Prueba que tambié lo es a b a + b 2 Ejercicio 3.4 Sea = y el criterio de la serie mayorate.) a y = a b. (H: Utiliza la desigualdad b dos series covergetes de térmios = positivos. Prueba que tambié lo es =2 a b a + b a y el criterio de la serie mayorate.) a b a + b. (H: Utiliza la desigualdad Como cosecuecia del criterio de la serie mayorate, se obtiee el siguiete criterio. 54
66 Teorema 3.7 (Criterio de comparació e el límite) Sea a y b dos series de térmios positivos y sea lím a b = λ. Etoces, Si 0 < λ < +, etoces a y b tiee el mismo carácter. Si λ = 0 y b es covergete, etoces a es covergete. Si λ = + y b es divergete, etoces a es divergete. Ejemplo 3. Cosidérese la serie Vamos a compararla co la serie, que sabemos es divergete (Ejem- log plo 3.0) =2 + lím log Este límite lo resolvemos por Stolz: lím log = = lím log log( + ) log = lím ( ) ( ) + log ( ) + + = lím = lím log + = log e = 0 Por tato, ambas series tiee el mismo carácter y, por tato, = es divergete. El icoveiete de este criterio reside e que ecesitamos otra serie coocida para poder compararla. Las más utilizadas para comparar so las llamadas series de Riema (ver el Ejemplo 3.5). 55
67 Para evitar este problema, veremos otros criterios e los que sólo se utiliza el térmio geeral a de la serie a ivestigar y, por tato, o se ecesita igua otra serie para comparar. Teorema 3.8 (Criterio de D Alambert) Sea a ua serie de térmios positivos y sea lím a + = λ. Etoces, a Si 0 λ <, etoces a es covergete. Si < λ +, etoces a es divergete. Este criterio se suele utilizar cuado el térmio geeral a costa de productos o cocietes. Notar que este criterio o determia el carácter de la serie cuado lím a + =. Cuado esto ocurre puede utilizarse el criterio siguiete. a Teorema 3.9 (Criterio de Raabe) Sea ( a ua serie de térmios positivos y sea lím a ) + = λ. Etoces, a Si λ <, etoces a es divergete. Si λ >, etoces a es covergete. Ejemplo 3.2 Sea la serie serie = a = 3! y aplicamos el criterio de D Alambert: 3. Idetificamos el térmio geeral de la! lím a + a = lím ( + ) 3 ( + )! 3! ( ) + 3 = lím + = 0 < y podemos cocluir que = 3! es covergete. 56
68 Ejemplo 3.3 Sea la serie geeral de la serie = a = y aplicamos el criterio de D Alambert: 3 5 (2 ). Idetificamos el térmio (2) 3 5 (2 ) (2) lím a + a = lím 3 5 (2 )(2 + ) (2)(2 + 2) 3 5 (2 ) (2) = lím = y o podemos cocluir ada. Aplicamos ahora el criterio de Raabe, utilizado que, segú el cálculo aterior, a + a = : ( lím a ) ( + = lím 2 + ) = lím a = lím = 2 < y etoces obteemos que = 3 5 (2 ) (2) es divergete. Ejercicio 3.5 Estudia el carácter de la series (a) = (!) 2 + (3)! y (b) (!) 2 (2)!. = (Sol.: (a) Covergete; (b) Covergete ) Ejercicio 3.6 Estudia el carácter de la serie + 2! =. Ejercicio 3.7 Estudia el carácter de la serie + (!) 2 =. 2 2 (Sol.: Covergete. ) (Sol.: Covergete. ) 57
69 Ejercicio 3.8 Estudia el carácter de la serie (3 + ) = (4 2). Ejercicio 3.9 Estudia el carácter de la serie + = (Sol.: Covergete. ) (!) 2 4. (2)! (Sol.: Divergete. ) El siguiete criterio es equivalete al criterio de D Alambert pero se utiliza e vez de éste cuado el térmio geeral a costa de potecias de expoete, 2, etc. Teorema 3.0 (Criterio de la raíz o de Cauchy) Sea a ua serie de térmios positivos y sea lím a = λ. Etoces, Si 0 λ <, etoces a es covergete. Si < λ +, etoces a es divergete. Ejemplo 3.4 Sea la serie = y aplicamos el criterio de la raíz: lím + si 3 a = lím = lím + si 3. Idetificamos el térmio geeral a = + si3 + si 3 = lím + si 3 Para calcular este límite, vamos a probar e primer lugar que + si 3 es ua sucesió acotada. E efecto, si si si etoces, aplicado el Teorema 2., y cocluimos que lím a = lím = + si 3 }{{} 0 + si 3 = 0 < }{{} acotada es covergete. 58
70 Ejercicio 3.20 Determia el carácter de la serie + = ( 2 3). (Sol.: Covergete. ) Ejercicio 3.2 Determia el carácter de la serie ( ) + =. 2 + Ejercicio 3.22 Determia el carácter de la serie + = (Sol.: Covergete. ) ( 2 + ) 2. (Sol.: Divergete. ) El criterio siguiete se suele utilizar cuado el térmio geeral a costa de potecias de expoete cualquiera. Teorema 3. (Criterio Logarítmico) Sea ( ) a ua serie de térmios log a positivos y sea lím = λ. Etoces, log Si λ <, etoces a es covergete. Si λ >, etoces a es divergete. Ejemplo 3.5 Vamos a estudiar la covergecia de ua familia de series, llamadas Series de Riema:, α R. Idetificamos el térmio geeral: α = a = α y aplicamos el criterio logarítmico: ( ) log a log α lím = lím log log = lím α log log = α Así, si α > la serie es covergete y si α < la serie es divergete. Si α = la serie queda = + α = 59 =
71 que es divergete. Resumiedo, =, (α R) α Covergete si α > Divergete si α Las series de Riema se utilizará a meudo e el criterio de comparació e el límite, sobre todo si el térmio geeral es u cociete de poliomios. E el ejemplo siguiete vemos su aplicació. Ejemplo 3.6 Determia el carácter de la serie = Solució: Vamos a compararla e el límite co la serie de térmio geeral d 3 = (que so los dos ifiitos de mayor orde que aparece e la serie 2 a estudiar). lím = lím = 5 por lo que la serie iicial tiee el mismo carácter que la serie y, siedo 2 ésta covergete, por ser ua serie de Riema de expoete α = 2 >, os permite cocluir que = es covergete. Ejercicio 3.23 Determia el carácter de la serie + = Ejercicio 3.24 Determia el carácter de la serie 3 + = 2 +. (Sol.: Covergete. ) (Sol.: Covergete. ) 60
72 Ejercicio 3.25 Determia el carácter de la serie + = 3 +. (Sol.: Covergete. ) Ejercicio 3.26 Determia el carácter de la serie + =2 [log(log())] log(). Ejercicio 3.27 Determia el carácter de la serie + = (Sol.: Covergete. ). log() (Sol.: Divergete. ) Teorema 3.2 (Criterio de Codesació) Sea a ua serie de térmios positivos, dode la sucesió {a } es decreciete, etoces las series tiee el mismo carácter. a y 2 k a 2 k Ejemplo 3.7 Determia el carácter de la serie k =2 log. Solució: Llamamos a =. Como { log } es ua sucesió creciete deducimos que {a } es decreciete. Así, podemos aplicar el criterio de log codesació y cocluir que log y + 2 k 2 k tiee el mismo log 2k =2 k= carácter. Estudiemos ahora esta última: k= 2 k 2 k log 2 k = + k= + log 2 k = k= k log 2 = log 2 k k= y resulta ser la serie armóica que es divergete. Cocluimos, pues, que es divergete. log =2 6
73 Ejercicio 3.28 Determia el carácter de la serie + =2 (log()) p, p N. (Sol.: Covergete si p >. ) Ejercicio 3.29 Determia el carácter de la serie + =3 log() log [(log())]. (Sol.: Divergete. ) Series alteradas Defiició 3.3 Ua serie = todo (i.e. sus térmios altera el sigo). a se dice alterada si a a + < 0, para Para series alteradas dispoemos del siguiete criterio: Teorema 3.4 (Criterio de Leibitz) Sea a co a + a < 0, para todo. Si la sucesió { a } es decreciete, etoces a es covergete lím a = 0 Notas: A ua serie alterada o se le puede aplicar iguo de los criterios vistos ateriormete para series de térmios positivos. Si la sucesió { a } es creciete etoces o puede teer límite 0 y así la serie será divergete, pero la sucesió { a } puede o ser i creciete i decreciete y, e este caso, o podremos aplicar el criterio de Leibitz. Toda serie alterada puede ser escrita de la forma forma = = ( ) a ó de la ( ) + a dode a > 0 (depediedo que sea egativos los térmios impares o pares, respectivamete). 62
74 Ejemplo 3.8 Determia el carácter de la serie ( ) +. Solució: Se trata de ua serie alterada. Veamos si cumple la hipótesis del criterio de Leibitz. Llamamos a = ( ) + ; por tato a =. Como {} es ua sucesió creciete, deducimos que {a } es decreciete. Por tato, podemos aplicar el criterio de Leibitz y al ser lím = 0 podemos cocluir que = ( ) + = es covergete. Ejemplo 3.9 Comprobar que la serie alterada diverge y explicar por qué o se cotradice el criterio de Leibitz. Solució: No se puede aplicar el criterio de Leibitz porque la sucesió de los valores absolutos de los térmios o es decreciete. No es covergete porque al agrupar los térmios de la forma: ( 2 ) + ( ) + ( ) +... obteemos la serie que es divergete y recuerda que si ua serie es covergete, cualquier reagrupació debe ser covergete (Teorema 3.4). Ejercicio 3.30 Determia el carácter de la serie + ( ) + = 2. (Sol.: Divergete. ) 63
75 Ejercicio 3.3 Determia el carácter de la serie + ( ) =. Ejercicio 3.32 Determia el carácter de la serie + ( ) = log(). (Sol.: Covergete. ) (Sol.: Covergete. ) Ejercicio 3.33 Determia el carácter de la serie ( ) + = ( )+ si. Ejercicio 3.34 Determia el carácter de la serie + = (Sol.: Covergete. ) + ( ). (Sol.: Divergete. ) 3.3. Covergecia absoluta y codicioal Defiició 3.5 Ua serie serie = a es covergete. = a se dice Absolutamete Covergete si la ( ) Ejemplo 3.20 La serie es covergete (Ejemplo 3.8) pero o = absolutamete covergete, ya que la serie de los valores absolutos o es covergete: ( ) + = divergete = = Ejercicio 3.35 Estudiar la covergecia y la covergecia absoluta de la serie: (Sol.: Covergete pero o absolutamete. ) 64
76 Nota: Está claro que para series de térmios positivos ( o de térmios egativos) los coceptos de covergecia y covergecia absoluta so equivaletes. Es más, si recordáis que el carácter de ua serie o depede del térmio e que empieza a sumar, podemos afirmar lo mismo para series co u úmero fiito de térmios egativos (o, respectivamete, de térmios positivos). E geeral la relació etre la covergecia y la covergecia absoluta viee dada por la siguiete propiedad: Teorema 3.6 Si a es absolutamete covergete, etoces a es covergete. Esta propiedad os da u uevo criterio para estudiar la covergecia de las series alteradas: Ejemplo 3.2 Cosideremos la serie: (2 ) 3 (2) Es ua serie alterada pero o podemos aplicarle el criterio de Leibitz porque los térmios, e valor absoluto, o forma ua sucesió decreciete. Estudiemos la covergecia absoluta: (2 ) 3 + (2) = + Si esta última la descompoemos e dos series: = = = ( (2 ) 3 + ) (2) 2 (2 ) 3 que es covergete, comparádola co 3 (2) 2 que es covergete, comparádola co 2 Etoces, como las dos so covergetes, cocluimos que la serie ( (2 ) 3 + ) (2) 2 = 65
77 es covergete, por lo que la serie primera resulta ser absolutamete covergete y, por tato, covergete. Defiició 3.7 Dadas dos series a y b, diremos que b es ua reordeació de a si la sucesió {b } se ha obteido a partir de {a } reordeado sus térmios. Defiició 3.8 Ua serie a se dice: Icodicioalmete covergete si la serie es covergete y cualquier reordeació de ella es covergete y suma lo mismo. Icodicioalmete divergete si la serie es divergete y cualquier reordeació de ella es divergete. Codicioalmete covergete si es covergete pero o icodicioalmete covergete. Codicioalmete divergete si es divergete pero o icodicioalmete divergete. El siguiete resultado simplifica el estudio de la covergecia codicioal: Teorema 3.9 La serie a es icodicioalmete covergete si, y sólo si, es absolutamete covergete. ( ) Ejemplo 3.22 La serie es codicioalmete covergete, ya que = es covergete (por el criterio de Leibitz) pero o absolutamete covergete (ver el Ejemplo 3.20). Si ua serie tiee u úmero fiito de térmios egativos (o de térmios positivos) sabemos que su covergecia implica covergecia absoluta. Por tato, para que ua serie sea codicioalmete covergete ha de teer ifiitos térmios positivos e ifiitos térmios egativos. Supoemos etoces ua serie a de maera que {a } tiee ifiitos térmios positivos {b } e ifiitos térmios egativos {c }. Etoces, 66
78 Teorema 3.20 Co la otació aterior se tiee las siguietes propiedades: b c } covergetes a icodicioalmete covergete. b c b c } ua es covergete a y la otra divergete icod. divergete. } divergetes a cod. covergete o cod. divergete. Además, e este último caso, si lím a = 0, podemos obteer ua reordeació o bie divergete o bie covergete. Ejemplo 3.23 Estudia la covergecia codicioal de la serie = a Solució: Cosideramos por separado los térmios positivos b y egativos c. b = = + c = = + = = (2 ) 2 covergete. 2 divergete. Etoces, la serie a es icodicioalmete divergete. Ejercicio 3.36 Estudia la covergecia y la covergecia absoluta de la serie (Sol.: Divergete. ) 67
79 Ejercicio 3.37 Estudia la covergecia y la covergecia absoluta de la serie! + 2 2! + 3 3! +... (Sol.: Icodicioalmete divergete. ) Ejercicio 3.38 Dada la serie de la cual sabemos que es covergete pero o absolutamete (Ejercicio 3.35); cosidera la siguiete reordeació ( + ) ( ) ( + + ) Qué podemos decir sobre su covergecia? Y sobre la covergecia absoluta? (Sol.: No absolutamete covergete y divergete. ) 3.4. Sumació de series Hasta ahora hemos visto métodos para determiar si ua serie es covergete o divergete. Cuado ua serie a es covergete sabemos que tiee ua suma fiita S. El objetivo de esta secció es calcular la suma de la serie. Este problema resulta más complicado de abordar que el estudio del carácter, dado que la suma es, e realidad, el límite de la sucesió de las sumas parciales y o siempre será factible poder calcularlo. Hemos estudiado ya la suma de ua serie geométrica y, co ua técica parecida, estableceremos la suma de alguos tipos más de series. (a) Series Aritmético-Geométricas So de la forma + = a b dode {a } es ua progresió aritmética (de distacia d) y {b } es ua progresió geométrica (de razó r). Etoces, a = a + d( ) =, 2,... b = b r =, 2,... 68
80 Se observa por simple sustitució que la serie o es covergete cuado r =. Vamos a calcular S e los otros casos: S = a b + a 2 b 2 + a 3 b a b + a b rs = a b 2 + a 2 b 3 + a 3 b a b + a b + de dode restado ambas expresioes resulta S ( r) = a b + [(a 2 a )b (a a )b ] a b + pero, como la diferecia etre dos térmios cosecutivos de ua progresió aritmética siempre es la distacia d, obteemos: S ( r) = a b + d [b 2 + b b ] a b + = a b + db [ r + r r ] a b + y ahora como r + r r = r r r obteemos y aislado S : S ( r) = a b + db r r r a b + S = a b r + db r r ( r) 2 a b + r Supoemos ahora que r <, etoces lím r = 0 lím a b + = lím(d( ) + a )b r = 0 lím S = a b r + drb ( r) 2 Por cotra si r > etoces lím r = y o existe lím S. Resumiedo, la serie aritmético-geométrica y e este caso suma exactamete = = a b es covergete sii r < a b = a b r + drb ( r) 2 (3.) 69
81 Ejercicio 3.39 Ecuetra la fórmula de la suma cuado la serie empieza a sumar desde = p. Ejemplo 3.24 Calcularemos la suma de la serie: = ( + 2) (2 + 2) Solució: Simplificado los térmios, se observa que correspode a ua serie aritmético-geométrica. = ( + 2) (2 + 2) = = = = por lo que aplicado la fórmu- de dode d =, r = 2, a = 3 y b = 2 3 la (3.), se obtiee = ( + 2) (2 + 2) ( 2 )2 = (b) Series Hipergeométricas So series de térmios positivos a + a = = α + β α + γ a que cumple la relació co α + β γ 0 Puede probarse que S = (α + γ)a + γa α + β γ 70
82 = Si supoemos ahora que la serie a es covergete, etoces ecesariamete debe ser lím a + = 0 y lím a + = 0 y así, S = lím S = = a = a γ γ α β (3.2) Nota: Para determiar los valores correctos de α, β y γ, la serie debe empezar a sumar desde =. Ejemplo 3.25 Sea la serie Solució: Como ( p ) = =p =p ( p )! p!( p)! resulta ( p ) = =p p!( p)!! Estudiemos primero su carácter mediate el criterio de D Alambert: llamado a = ( p ) obteemos p!( p)!! lím a + a = lím p!( + p)! ( + )! p!( p)!! = lím + p + Aplicamos ahora el criterio de Raabe ( lím a ) + = lím a = = lím p + = p ( + p ) + 7
83 Así si p > la serie es covergete. El caso p = lo estudiaremos más adelate. Además, la serie es hipergeométrica porque a + a = + p + Ahora bie, para determiar la suma y, más cocretamete, los valores correctos de α, β, γ la serie debe empezar a sumar desde =. Para coseguirlo haremos u cambio de variable: =p p!( p)!! = = +=p+ + p= p!( p)!! p!( p)!! k=+ p = k= p!(k )! (k + p )! Llamado ahora a k = p!(k )! (k + p )! k obteemos a k+ a k = p!k! (k + p)! p!(k )! (k + p )! = k k + p de dode α =, β = 0 y γ = p co α + β γ = p y, aplicado la fórmula (3.2), se obtiee =p p!( p)!! = k= p!(k )! (k + p )! = p p = p p (p > ) Fialmete, si p =, resulta que ( ) =, de dode =p p!( p)!! = = que es divergete. 72
84 (c) Series telescópicas Ua serie + = a se dice telescópica si el térmio geeral a puede descompoerse de la forma a = b b es decir, es la diferecia etre dos térmios cosecutivos de otra sucesió. E este caso, es posible hallar la suma parcial S y calcular su límite. Ejemplo 3.26 Calcula la suma de la serie = ( + ). Solució: La serie es telescópica puesto que, al descompoer fraccioes simples, resulta Etoces, para calcular S hacemos: ( + ) = + a = 2 a 2 = 2 3 a 3 = 3 4. a = a = + a + a a = + ( + ) e Ahora, al sumar estas igualdades, resulta que, e la parte de la derecha se cacela los térmios dos a dos (salvo el primero y el último) y e la izquierda queda a + a a = S, por lo que y, por tato, = ( + ) = lím S = + S = lím ( ) = + 73
85 Ejercicio 3.40 Calcula la suma de la serie + =2 2, descompoiédola previamete e fraccioes simples. (Sol.: 3 4 ) Ejercicio 3.4 Calcula la suma de la serie + =2 ( + )( + 2), descompoiédola previamete e fraccioes simples. Ejercicio 3.42 Calcula la suma de la serie =2 log ( ) 2. (Sol.: + ) (Sol.: log 2 ) 3.5. Problemas adicioales Ejercicio 3.43 Averigua el carácter de las series (a) log() 2 (d) (g) [log()] (j) si (π/) (b) 2( )+ e + e (c) cos(π) (e) (2)! 5 (f)! (h) 7! (i) cos() 2 (Sol.: So covergetes (a), (b), (g), (h), (i) y (j). ) Ejercicio 3.44 Averigua el carácter de la serie! (2 + )(2 + 2) (2 + ) (Sol.: Covergete ) 74
86 Ejercicio 3.45 Estudia el carácter de las series: (a) ( 2 + ) (b) 3 5 (c) ( 7) (d) log (2 + 3 ) 2 (e) ( log + ) (f) ( ) 3 ta (g) 5 3 ( 2 + ) (j) ( ) si (m) ( ( 2 + ) 2 ) π si 3 (h) ( + )2 (i) (k)! 3 (l) log() + () ( )! (Sol.: So covergetes: (b), (f), (g), (h), (m) y (). ) Ejercicio 3.46 Estudia la covergecia y la covergecia absoluta de la serie 2 log log log log (H: Utilizar la desigualdad ( + ) ( < e < + ) + para demostrar que los valores absolutos de los térmios de la serie forma ua sucesió decreciete) Ejercicio 3.47 Calcula la suma de la serie (Sol.: Codicioalmete covergete ) = ( 2 ) 3. (Sol.: 2 ) Ejercicio 3.48 Calcula la suma de la serie + 4 = ( + 2), descompoiédola previamete e fraccioes simples. (Sol.: 3 ) 75
87 Ejercicio 3.49 Calcula la suma de la serie + = (2 + )(2 + 3), descompoiédola previamete e fraccioes simples. Ejercicio 3.50 Calcula la suma de la serie ( ) + = log 2. = =2 (Sol.: 2 ) (4 ) 2, sabiedo que (Sol.: 4 log 2 ) 76
88 Tema 4 Series de Potecias Ua expresió de la forma a 0 + a (x c) + a 2 (x c) a (x c) +... = recibe el ombre de serie de potecias cetrada e c. =0 a (x c) Ua serie de potecias puede ser iterpretada como ua fució de x f(x) = =0 a (x c) cuyo domiio es el cojuto de los x R para los que la serie es covergete y el valor de f(x) es, precisamete, la suma de la serie e ese puto x. Las series de potecias, vistas como fucioes, tiee u comportamieto bueo, e el setido de que so fucioes cotiuas y derivables de cualquier orde. Más aú, su fució derivada es, otra vez, ua serie de potecias. Desde u puto de vista más práctico, las series de potecias aproxima a su fució suma. Es decir, la suma parcial de orde, que o es más que u poliomio de grado a lo sumo, represeta ua aproximació a la fució suma e su domiio de covergecia. E la siguiete figura, Fig. 4., puede verse la fució f(x) = e x juto co alguas aproximacioes mediate sumas parciales de su serie de potecias. 77
89 Figura 4.: Aproximació a e x por su serie de potecias 4.. Radio de covergecia Nuestro objetivo ahora será determiar el domiio de ua serie de potecias. Por ua parte está claro que el cetro c siempre está e el domiio ya que f(c) = =0 a (c c) = a 0 Puede ocurrir que la serie sólo sea covergete e x = c, pero, e geeral, 78
90 el campo de covergecia será u itervalo; como os idica el resultado siguiete. Teorema 4. Sea =0 tres afirmacioes siguietes:. La serie sólo coverge e x = c. a (x c). Etoces es cierta ua, y sólo ua, de las 2. Existe R > 0 de maera que la serie coverge (absolutamete) si x c < R y diverge si x c > R. 3. La serie coverge para todo x R. Al úmero R se le llama Radio de covergecia de la serie. Para uificar todos los casos, etedemos e el caso () que R = 0, y e el caso (3) que R = +. Por tato el domiio o campo de covergecia de ua serie de potecias es siempre u itervalo, ocasioalmete u puto, que llamaremos itervalo de covergecia. Notar que el teorema precedete o afirma ada respecto de la covergecia e los extremos del itervalo, c R y c + R. Veremos seguidamete ua fórmula para calcular el radio de covergecia: Teorema 4.2 (Cauchy-Hadamard) Sea Etoces, A = 0 R = + A = + R = 0 =0 a (x c) y sea A := lím a. 0 < A < + R = A Nota: El símbolo lím a represeta el límite superior de la sucesió {a } el cual viee defiido como el mayor de los límites de las subsucesioes covergetes de {a }. Obviamete, si la sucesió {a } es covergete, etoces lím a = lím a por lo que cocluimos que 79
91 Si existe lím a = A R = A Si existe lím a + a = A R = A La utilizació de u criterio u otro depederá de la forma que tega el térmio a. Ejemplo 4. Cosidera la serie de potecias + x + (2!)x 2 + (3!)x (!)x +... = E esta serie a =! de dode =0 (!)x A = lím a + a = lím ( + )!! = lím ( + ) = + R = 0 Así pues, la serie sólo coverge e x = 0. Ejemplo 4.2 Sea la serie de potecias = x. Para calcular su radio de covergecia llamamos a = y obteemos A = lím 2+ a = lím = lím 2+ = 0 R = Así pues, la serie es covergete para cualquier valor de x R. Luego el itervalo de covergecia es I = R =], + [. Ejemplo 4.3 Sea la serie de potecias = covergecia llamamos a = 3 4 y obteemos 3 4 x. Para calcular su radio de A = lím 3 a = lím 4 = lím 80 ( ) 3 4 = 4 R = 4
92 Así pues, la serie es (absolutamete) covergete si x < 4 y divergete si x > 4. Para averiguar la covergecia e los extremos del itervalo será ecesario hacer el estudio particular. x = 4 = = 3 = (divergete) x = 4 = 3 4 ( 4) = ( ) 3 = (divergete) Cocluimos, fialmete, que el itervalo de covergecia es I =] 4, 4[. Ejemplo 4.4 Sea la serie de potecias = covergecia llamamos a = y obteemos x. Para calcular su radio de A = lím a = lím = lím = R = Así pues, la serie es (absolutamete) covergete si x < y divergete si x >. Para averiguar la covergecia e los extremos del itervalo será ecesario realizar el estudio particular. x = = = + = (divergete) x = = ( ) (covergete) Cocluimos, fialmete, que el itervalo de covergecia es I = [, [. Ejercicio 4. Calcula el radio de covergecia de la serie = (2x) 2. (Sol.: R = 2 ) 8
93 Ejercicio 4.2 Calcula el itervalo de covergecia de la serie Ejercicio 4.3 Calcula el itervalo de covergecia de la serie icluyedo el estudio de la covergecia e los putos extremos. =0 x!. (Sol.: I = R ) =0 (3x) (2)!, (Sol.: I =], + [= R ) ( ) + x Ejercicio 4.4 Calcula el itervalo de covergecia de la serie, 4 = icluyedo el estudio de la covergecia e los putos extremos. (Sol.: I =], ] ) Ejercicio 4.5 Calcula el itervalo de covergecia de la serie icluyedo el estudio de la covergecia e los putos extremos. =!x (2)!, (Sol.: I =], + [= R ) Ejercicio 4.6 Calcula el itervalo de covergecia de la serie de potecias ( ) + (x 5) 5, icluyedo el estudio de la covergecia e los putos = extremos. (Sol.: I =]0, 0] ) Ejercicio 4.7 Calcula el itervalo de covergecia de la serie de potecias ( ) + (x c) c c R, icluyedo el estudio de la covergecia e los = putos extremos. (Sol.: I =]0, 2c] si c > 0, I = [2c, 0[ si c < 0 ) Cuado las potecias o so cosecutivas se utiliza u cambio de variable para calcular el radio de covergecia. 82
94 3 Ejemplo 4.5 Sea la serie de potecias 4 x2. Como las potecias o = so cosecutivas, o puede aplicarse directamete el criterio del teorema de Cauchy-Hadamard. Realizaremos, previamete, u cambio de variable. = x2 = 4 (x2 ) 3 = 4 t = = para esta última calculamos el radio de covergecia, llamado a = 3 4, y obteemos R = 4 (es justo el Ejemplo 4.3). Así, = por lo que, deshaciedo el cambio, es decir, = = 3 4 t es covergete para t < 4, 3 4 (x2 ) es covergete para x 2 < 4, 3 4 x2 es covergete para x < 2, y cocluimos que el radio de covergecia es R = 2. Faltaría estudiar el comportamieto de la serie e los extremos del itervalo, pero ésto se deja como ejercicio al lector. Ejercicio 4.8 Calcula el itervalo de covergecia de la serie de potecias + ( 2x). = (Sol.: I =] 2, 2 [ ) Ejercicio 4.9 Calcula el itervalo de covergecia de la serie =0 ( ) x 2.! (Sol.: I = R ) 83
95 4.2. Propiedades Hemos visto que ua serie de potecias defie ua fució e u itervalo. Veremos ahora qué propiedades cumple esta fució. Teorema 4.3 Sea f(x) la fució defiida como ua serie de potecias f(x) = =0 a (x c) co radio de covergecia R > 0. Etoces,. f es cotiua e todo puto iterior del itervalo de covergecia. 2. f es derivable e todo puto iterior del itervalo de covergecia y, además, f (x) = = a (x c) teiedo esta última serie radio de covergecia R (derivació térmio a térmio). 3. f es itegrable e el itervalo de covergecia y, además, f(x)dx = =0 (a (x c) )dx = =0 a + (x c)+ + C teiedo esta última serie radio de covergecia R (itegració térmio a térmio). Ejemplo 4.6 Cosideramos la fució f(x) = = x. Hemos visto e u ejemplo aterior que el itervalo de covergecia era [, [. Etoces la fució derivada puede calcularse derivado térmio a térmio: f (x) = = x = + = x Sabemos, por la propiedad aterior, que el radio de covergecia para esta ueva serie cotiúa siedo R =. Veamos qué ocurre e los extremos del itervalo: 84
96 x = x = = = = = que es divergete, ( ) que es divergete. Así pues, la serie derivada coverge e ], [. Veamos ahora qué ocurre co la itegració. De uevo, podemos itegrar térmio a térmio. x + f(x)dx = = x + ( + ) + C = De uevo sabemos que el radio de covergecia para esta ueva serie cotiúa siedo R =. Veamos qué ocurre e los extremos del itervalo: = x = = + + ( + ) = ( + ) = que es covergete; x = = ( ) + ( + ) que es covergete. Así pues, la serie itegral coverge e [, ]. Nota: Observa e el ejemplo aterior que al derivar hemos perdido u puto del itervalo de covergecia, mietras que al itegrar hemos gaado uo. E geeral, si embargo, el resultado correcto es Al derivar ua serie o se puede gaar extremos del itervalo de covergecia. Al itegrar ua serie o se puede perder extremos del itervalo de covergecia. Ejercicio 4.0 Siedo f(x) la fució defiida por las serie de potecias ( ) + (x 5) 5, calcula el itervalo de covergecia de f(x), f (x) y = 85
97 f(x) dx, icluyedo el estudio de los putos extremos. (Sol.: I =]0, 0] para f y f ; I = [0, 0] para f ) Ejercicio 4. Siedo f(x) la fució defiida por la serie de potecias ( ) ( + )( + 2) x, calcula el itervalo de covergecia de f(x), f (x) y =0 f(x) dx, icluyedo el estudio de los putos extremos. (Sol.: I = [, ] para f y f; I =], ] para f ) Ejercicio 4.2 Siedo f(x) la fució defiida por las serie de potecias ( ) + x 2, calcula el itervalo de covergecia de f(x), f (x) y 2 = f(x) dx, icluyedo el estudio de los putos extremos. (Sol.: I = [, ] para f y f; I =], [ para f ) Otras propiedades iteresates so las siguietes. Teorema 4.4 Sea f(x) = =0 e el mismo itervalo I. Etoces, a (x c) y g(x) = =0 b (x c) defiidas. f(x) + g(x) = =0 (a + b )(x c), x I 2. αf(x) = α a (x c) = =0 =0 αa (x c), x I E el caso de series de potecia cetradas e c = 0, se cumple además 86
98 Teorema 4.5 Sea f(x) = a x defiida e el itervalo I. Etoces, =0. f(αx) = 2. f(x N ) = a (αx) = =0 =0 a (x N ) = =0 =0 a α x, a x N, x / αx I x / x N I Ejemplo 4.7 Calcular ua primitiva de la fució f(x) = e x2. Solució: Sabemos que e x = aterior: Ahora, itegrado e x2 dx = e x2 = =0 =0 =0 x. Etoces aplicado la proposició! (x 2 )! = =0 x 2! x 2 +! dx = x 2+ (2 + )! + C =0 E particular, F (x) = =0 x 2+ (2 + )! es ua primitiva de ex Desarrollo de fucioes e serie de potecias Hemos visto que ua serie de potecias defie ua fució e u itervalo I. Se aborda ahora el problema cotrario. Dada ua fució f(x) se trata de ecotrar ua serie de potecias =0 a (x c) 87
99 de maera que f(x) = =0 para todo x del itervalo de covergecia. a (x c) Evidetemete, tales fucioes debe ser cotiuas e idefiidamete derivables e su itervalo de covergecia y esto permite deducir además como debe ser los térmios de ua serie de potecias cuya suma es ua determiada fució f: Teorema 4.6 Si f(x) = =0 a (x c), x ]c R, c + R[ etoces, a = f () (c)! A la serie =0 f () (c) (x c) la llamaremos serie de Taylor de f e c.! Desarrollos de Taylor Coviee recordar ahora el coocido teorema de Taylor que permite aproximar ua fució por u poliomio de grado. Teorema 4.7 (Taylor) Sea f ua fució cotiua y co derivada cotiua hasta el orde e u itervalo I = [c R, c + R] y derivable de orde + e ]c R, c + R[. Si x I, existe u puto ξ etre c y x tal que f(x) = f(c) + f (c)(x c) + f (c) (x c) f ( )(c) (x c) } 2! {{! } T (x) + f (+ )(ξ) ( + )! (x c)( + ) }{{} R (x) 88
100 Los térmios T (x) forma u poliomio de grado a lo sumo, llamado poliomio de Taylor, mietras que el último térmio R (x) se llama el resto de Lagrage. Este teorema permite aproximar el valor de ua fució mediate u poliomio. Ejemplo 4.8 Aproxima la fució f(x) = de grado 3. Utiliza dicho poliomio para aproximar error cometido. Solució: + x mediate u poliomio,2. Da ua cota del. Basta calcular las derivadas hasta el orde 4. Tomaremos como puto de cálculo el valor a = 0. f(x) = ( + x) /2 f(0) = f (x) = 2 ( + x) 3/2 f (0) = 2 f (x) = 3 4 ( + x) 5/2 f (0) = 3 4 Fialmete, f (x) = 5 8 ( + x) 7/2 f (0) = 5 8 f (4) (x) = 05 6 ( + x) 9/2 f (4) (ξ) = 05 ( + ξ) 9/2 6 f(x) T 3 (x) = f(0) + f (0)x + f (0) x 2 + f (0) x 3 2! 3! por lo que, 2. Como Por tato, f(x) x 2 + 3x2 8 5x3 48,2 = f(0,2) basta tomar x = 0,2 e el poliomio aterior. 89
101 0,2, (0,2)2 5(0,2) El error viee dado por el térmio ɛ = f 4 (ξ) x 4 4! siedo x = 0,2 y 0 < ξ < 0,2. Podemos escribir, pues, 0,925 ɛ = 05 (0,2)4 4! 6( + ξ) 9/2 = 05(0,2)4 384( + ξ) 9/2 Ahora hay que elimiar ξ de la fórmula aterior acotado la fució por su valor máximo (e este caso, se trata de escribir el deomiador más pequeño posible, teiedo e cueta que 0 < ξ < 0,2 ): ɛ = 05(0,2)4 05(0,2)4 < 384( + ξ) 9/2 384 La aproximació es regular (2 o 3 cifras exactas). 0, Ejercicio 4.3 Aproxima la fució f(x) = x si x mediate u poliomio de grado o mayor que 3. Utiliza dicho poliomio para aproximar ( ) 3 si 3 co dos decimales de exactitud. Justifica la exactitud obteida. (Sol.: f(x) x 2 ; 3 si ( 3) 0,; Error < 0,00257) ) Hemos visto que si ua fució admite desarrollo e serie de potecias, esta serie debe ser ecesariamete su correspodiete serie de Taylor. No obstate, la serie de Taylor de f e c o tiee porque teer de suma a la propia fució f. Para garatizarlo teemos el siguiete resultado. Teorema 4.8 Si f es ua fució idefiidamete derivable e u itervalo abierto cetrado e c y si R (x) represeta el resto de Lagrage de la fórmula de Taylor, etoces f(x) = =0 f () (c) (x c) lím R (x) = 0! 90
102 Co el siguiete corolario tedremos ua forma más fácil de aplicar la propiedad aterior: Corolario 4.9 Si existe ua costate K > 0 de forma que f () (x) K, x I, 0 etoces f(x) = =0 f () (c) (x c) x I! Ejemplo 4.9 Sea f(x) = si x. Ecuetra u desarrollo e serie de potecias. Solució: Como etoces, f () (x) = si ( π ) 2 + x, = 0,, 2,... { ( f () (0) = si π ) ( ) k si = 2k + ( impar) = 2 0 si = 2k ( par) y obteemos, pues, que la serie de Taylor de f e x = 0 es k=0 ( ) k x 2k+ (2k + )! Calculamos el radio de covergecia de esta serie. Como las potecias o so cosecutivas realizaremos u cambio de variable. =0 ( ) x 2+ (2 + )! = x = x = x =0 =0 =0 ( ) x 2 (2 + )! ( ) (x 2 ) (2 + )! ( ) t (2 + )! 9
103 Para esta última serie, llamado a = ( ) (2 + )! se tiee A = lím a + a = lím (2 + )! (2 + 3)! = lím (2 + 3)(2 + 2) = 0 R = + Es decir, la serie coverge t R. Etoces, deshaciedo el cambio, la serie origial es covergete x 2 R, o sea, x R. Falta demostrar que la serie suma exactamete si x, es decir, =0 ( ) x 2+ (2 + )! = si x xɛr Ahora bie, como f () (x), x R, = 0,,... basta aplicar el Corolario 4.9 para cocluir que si x = =0 ( ) x 2+, x R (2 + )! De forma similar se prueba que cos x = e x = =0 =0 ( + x) α = ( ) x 2, x R (2)! x!, x R =0 siedo α R y ( ) α := ; 0 ( ) α x, ( ) α := x < (serie biómica). factores α(α ) (α ( )), si! 92
104 Otros desarrollos E geeral, el método de calcular la serie de Taylor o resulta muy operativo, dada la dificultad de ecotrar la derivada ésima o, auque esto sea posible, la dificultad de demostrar que lím R (x) = 0. Veremos ahora otros procedimietos para ecotrar el desarrollo de ua fució e serie de potecias. Básicamete se trata de obteer por derivació, itegració o trasformacioes elemetales ua fució de la cual coozcamos su desarrollo. Ejemplo 4.0 Desarrollo e serie de potecias de la fució f(x) = + x. Solució: Recordemos que para ua serie geométrica: Por tato, =0 x = x, x < + x = + ( x) = ( x) = =0 =0 ( ) x, x < Este problema tambié se podría haber resuelto teiedo e cueta que = ( + x) + x que correspode a ua serie biómica de expoete α = y aplicado el desarrollo coocido (pág. 92) se llega a la misma coclusió si más que teer e cueta que ( ) = ( ). Ejemplo 4. Desarrollo de f(x) = log x Solució: Recordemos que la serie biómica de expoete α = verifica =0 ( ) x = + x, x < 93
105 Por tato, f (x) = x = + + (x ) = ( ) (x ), x < =0 Recuperamos la fució f itegrado: f(x) = Así, f (x)dx = log x = =0 =0 ( ) (x ) dx = =0 ( ) + (x )+ + C, x < ( ) + (x )+ +C, x < Para calcular C basta evaluar la expresió aterior e u valor de x. Por secillez, se elige el cetro de la serie, x =. Ates de substituir, desarrollamos el sumatorio: log x = =0 ( ) + (x )+ +C = (x )+ 2 (x )2 + 3 (x ) C por lo que al evaluar la serie e x =, obteemos log = 0 + C C = 0 y, fialmete, log x = =0 ( ) (x )+ + E el ejemplo aterior, hemos probado que log x = =0 ( ) + (x )+, x < Estudiemos ahora qué pasa co los extremos del itervalo: x = 0 =0 ( ) + ( )+ = + =0 94 que es divergete.
106 x = 2 =0 ( ) + (2 ( ) )+ = + =0 que es covergete. Pero, podemos afirmar que e x = 2 la serie suma exactamete log 2? E geeral, la respuesta es o. El teorema que veremos a cotiuació os dará ua codició suficiete para que podamos garatizarlo. Teorema 4.0 (Abel) Sea f(x) = =0 a (x c), x c < R. Si f es cotiua e c + R y la serie es covergete e x = c + R etoces se verifica que f(c + R) = =0 a (c + R c) = =0 a R Aálogamete para el extremo iferior: si f es cotiua e c R y la serie es covergete e x = c R etoces se verifica que f(c R) = =0 a (c R c) = =0 a ( R) Ejemplo 4.2 Volviedo al ejemplo aterior, habíamos visto que log x = =0 ( ) + (x )+, x < Ahora, la serie es covergete e x = 2 y la fució f(x) = log x es cotiua e x = 2, etoces aplicado el teorema de Abel resulta que log 2 = =0 ( ) + Ejercicio 4.4 Desarrolla e serie de potecias cetrada e c = 0 la fució 3 x (Sol.: 3 2 =0 ( 2) x x < 2 )
107 Ejercicio 4.5 Desarrolla e serie de potecias cetrada e c = 0 la fució ( + x) 2. (Sol.: = ( ) x x < ) Ejercicio 4.6 Desarrolla e serie de potecias cetrada e c = 0 la fució 2 ( + x) 3. (Sol.: =2 ( ) ( )x 2 x < ) Ejercicio 4.7 Desarrolla e serie de potecias cetrada e c = 0 la fució log(x + ). (Sol.: =0 ( ) + x+ x ], ] ) Ejercicio 4.8 Desarrolla e serie de potecias cetrada e c = 0 la fució 4x 2 +. (Sol.: =0 ( ) 4 x 2 x < 2 ) Ejercicio 4.9 Desarrolla e serie de potecias cetrada e c = 0 la fució cos x. (Sol.: =0 ( ) (2)! x2 ) 96
108 4.4. Problemas adicioales Ejercicio 4.20 Calcula el itervalo de covergecia de las series siguietes, icluyedo el estudio de los putos extremos: (a) ( x ( ) x k ) k R; (b) ; (c) (e) (g) =0 ( ) + x ; =0 =0 =0 = (d) = (2)!( x 2 ) ; =0 ( ) x ( + )( + 2) ; (f) =0 (x 2) ( + )3 + ; (h) =0 =0 ( ) (x 4) 3 ; ( ) + (x ) + ; + ( ) + x (i) ; (j) (2 + ) x2+. (k) =0 x 2+ (2 + )! ; (Sol.: (a) I =] k, k [, (b) I =], [, (c) I =], [, (d) I = {0}, (e) I = [, ], (f) I =], 7[, (g) I = [, 5[, (h) I =]0, 2], (i) I = [, ], (j) I =], [ y (k) I = R. ) Ejercicio 4.2 Siedo f(x) la fució defiida por la serie f(x) = = ( x 2 ), calcula el itervalo de covergecia de f(x), f (x) y f(x) dx, icluyedo el estudio de los putos extremos. Ejercicio 4.22 Cosidera la serie de potecias: (Sol.: I =] 2, 2[ para f y f ; I = [ 2, 2[ para f ) ( ) 7 ( + 6) (9 + 6) x =0 97
109 (a) Calcula el radio de covergecia de la serie. (b) Estudia la covergecia e x =, y e caso de ser covergete, calcula la suma. (c) Verifica, e x =, las hipótesis del criterio de Leibitz para series alteradas? (d) Es absolutamete covergete e x =? (Sol.: (a) R = ; (b) Covergete y suma Ejercicio 4.23 Dada la serie de potecias = ; (c) Si; (d) Si. ) ( + )( + 2) (2 + )! x. (a) Determia el radio de covergecia de la serie. (b) Estudia la covergecia de la serie e x = 4 y e x =. (c) Estudia la covergecia e x = 4. (Sol.: (a) R = 4 ; (b) Divergete e x = 4 y x = ; (c) Divergete. ) Ejercicio 4.24 Aproxima la fució f(x) = x l( + x) mediate u poliomio de grado 3. Utiliza dicho poliomio para aproximar 0,2 l(,2). Obté ua cota del error cometido. (Sol.: f(x) x 2 2 x3 ; 0,2 l(, 2) = 0,036 ± 0,00053 ) Ejercicio 4.25 Aproxima la fució f(x) = x 2 l x mediate u poliomio de grado 2, expresado e potecias de (x ). Utiliza dicho poliomio para aproximar 4 l ( 2) co dos decimales de exactitud. Justifica la exactitud obteida. (Sol.: f(x) x (x )2 ; 4 l ( 2) = 0,25 ± 0,083 ) Ejercicio 4.26 Se cosidera la fució f(x) = l( + x). (a) Aproxima la fució por u poliomio de grado 4. 98
110 (b) Utiliza el poliomio aterior para aproximar l( 0,95) y acota el error cometido. (Sol.: (a) x 2 x2 4 + x3 6 x4 8 ; (b) l( 0,95) 0, ± 4, ) Ejercicio 4.27 Se cosidera la fució f(x) = l( + x). (a) Desarrolla e serie de potecias la fució g(x) = + x. (b) Calcula la derivada de f(x). (c) Desarrolla e serie de potecias la fució f(x). (Sol.: (a) ( ) x ; x < ; (b) =0 2( + x) ; (c) 2 ( ) x + ; x < ) + Ejercicio 4.28 Desarrolla e serie de potecias la fució + x + x 2 idicado cuál es el radio de covergecia. (H: Expresa el radicado +x+x 2 e la forma a 2 + (x + b) 2 para aplicar la serie biómica) (Sol.: 3 4 ( ) /2 4 =0 3 ( x + 2) 2 si x < 2 ) Ejercicio ( 4.29 ) Aplica el ejercicio aterior para calcular la suma de la serie /2 =0. (H: Toma u valor adecuado de x e el desarrollo aterior) 3 (Sol.: 2 3 ) Ejercicio 4.30 Desarrolla e serie de potecias cetrada e c = 0 la fució f(x) = e x2 /2. (Sol.: =0 2! x2 x R ) Ejercicio 4.3 Desarrolla e serie de potecias cetrada e c = 0 la fució f(x) = 4x 7 2x 2. (H: Expresa la fracció como suma de fraccioes + 3x 2 simples, hallado las raíces del deomiador) 99
111 (Sol.: =0 ( ) 3( ) x x < 2 ) E los ejercicios siguietes se trata de, mediate derivació o itegració de la fució dada, relacioarla co ua fució de desarrollo coocido y, a partir de este, hallar el desarrollo de la fució origial. Ejercicio 4.32 Desarrolla e serie de potecias cetrada e c = 0 la fució f(x) = arcta 2x. (Sol.: 2 =0 ( ) x2+ x 2 ) Ejercicio 4.33 Desarrolla e serie de potecias cetrada e c = 0 la fució f(x) = arcsi x. (Sol.: =0 ( ) /2 ( ) 2 + x2+ x ) Ejercicio 4.34 Desarrolla e serie de potecias cetrada e c = 0 la fució f(x) = arcsi x (H: Utiliza el ejercicio aterior). x ( ) /2 ( ) (Sol.: 2 x2+ x ) Ejercicio 4.35 Desarrolla e serie de potecias cetrada e c = 0 la fució f(x) = si 2 x. (Sol.: =0 =0 ( ) 4 (2 + )!( + 2) x2+2 x R ) Ejercicio 4.36 Desarrolla e serie de potecias cetrada e c = 0 la fució f(x) = log(x 2 + ). (Sol.: =0 ( ) + x2+2 x [, ] ) 00
112 Tema 5 Fucioes de varias variables Supogamos que teemos ua placa rectagular R y determiamos la temperatura T e cada uo de sus putos. Fijado u sistema de referecia, T es ua fució que depede de las coordeadas (x, y) de cada uo de los putos de R. La fució que describe este feómeo T = f(x, y), (x, y) R es u ejemplo típico de ua fució de dos variables; e este caso, las coordeadas del puto dode evaluamos la temperatura. No es difícil ecotrar ejemplos de feómeos que a la hora de describirlos ecesitemos utilizar fucioes de tres, cuatro o más variables. La defiició formal de fució de varias variables es la siguiete: Defiició 5. Sea D u subcojuto de R. Ua fució f de D e R se llama u campo escalar o ua fució real de variables. La fució f asiga, pues, a cada vector x = (x, x 2,..., x ) D R u valor real f(x). Las fucioes de varias variables so eseciales e muchos problemas importates de la ciecia, la igeiería, la ecoomía, etc... De hecho, cualquier fórmula que proporcioe ua relació etre ua magitud a partir de los valores de otras magitudes es, e realidad, ua fució. Vamos a ver alguos ejemplos: 0
113 Ejemplo 5. La magitud de la fuerza gravitatoria ejercida por u cuerpo de masa M situado e el orige de coordeadas sobre u cuerpo de masa m situado e el puto (x, y, z) viee dada por F (x, y, z) = GmM x 2 + y 2 + z 2 La ley de los gases ideales dice que la presió P de u gas es ua fució del volume V y la temperatura T segú la ecuació dode c es ua costate. P = ct V La desviació S e el puto medio de ua viga rectagular cuado está sujeta por ambos extremos y soporta ua carga uiforme viee dada por S(L, w, h) = CL3 wh 3 dode L es la logitud, w la achura, h la altura y C ua costate. Nota: El domiio de u campo escalar f (deotado por Dom(f)) es el subcojuto de R dode está defiida la fució. E muchas ocasioes, ua fució viee dada por ua expresió algebraica y su domiio o viee dado explícitamete. Etedemos, e este caso, que el domiio es el cojuto de todos los putos para los que la defiició de f tiee setido. La image o recorrido de u campo escalar (deotado por Im(f)) es el subcojuto de R dado por todos los valores que toma la fució f; es decir, Im(f) := {f(x) : x Dom(f)} La gráfica de f es el subcojuto de R +, defiido como graf(f) := {(x, f(x)) : x Dom(f)} Evidetemete, sólo podemos represetar gráficamete las fucioes de ua variable (su gráfica está e R 2 ) y las fucioes de dos variables (su gráfica está e R 3 ). 02
114 5.. Represetació de fucioes Ua forma de obteer iformació sobre el feómeo descrito por ua fució de dos variables es estudiar su represetació gráfica. Ésta o es ua tarea secilla pero dispoemos de alguos métodos que permite haceros ua idea de su comportamieto. Se trata de cortar la gráfica de la fució co plaos paralelos a los plaos coordeados. Empezaremos co plaos verticales. Defiició 5.2 Para ua fució f(x, y), la fució que se obtiee al mateer la variable x fija y variado la variable y se llama secció trasversal de f co x fija. Aálogamete se defie ua secció trasversal de f co y fija. Ejemplo 5.2 Vamos a calcular la secció trasversal, para x = 2, de la fució f(x, y) = x 2 + y 2. Solució: Tal y como se observa e la Figura 5., la secció trasversal es la curva obteida al cortar la gráfica de f(x, y) co el plao vertical de ecuació x = 2. Figura 5.: Secció trasversal co x fija 03
115 La secció trasversal que hemos de ecotrar es, precisamete, f(2, y) = 4+y 2. Por tato es ua fució de y, digamos g, defiida como g(y) = 4+y 2. Se trata de ua parábola simétrica respecto del eje x. E geeral, obteemos las seccioes trasversales de f como fucioes de y haciedo x = c e f(x, y). Las seccioes so, por tato, g c (y) = c 2 + y 2, c R. Ejercicio 5. Calcular las seccioes trasversales, primero fijado la variable x y después la variable y, del campo escalar f(x, y) = x 2 y 2. (Sol.: g b (x) = x 2 b 2, g c (y) = c 2 y 2 ) ) Otra maera de obteer iformació sobre ua fució de dos variables es por medio de las llamadas curvas de ivel, que correspode a la curva obteida al cortar la gráfica de z = f(x, y) por u plao horizotal de ecuació z = c. Por tato, las curvas de ivel de f(x, y) so los subcojutos del domiio co ecuacioes de la forma: f(x, y) = c, dode c es u valor e Im(f). La idea de las curvas de ivel es u método de represetar superficies que utilizamos e la elaboració de mapas. Para represetar terreos motañosos es práctica comú dibujar curvas que ue los putos de la misma altura. Ua colecció de estas curvas, rotuladas de forma adecuada, da ua buea idea de las variacioes de altitud de ua regió. Ejemplo 5.3 Calculemos las curvas de ivel del campo escalar z = 4 x y (cuya gráfica es u plao). Haciedo z = c 4 x y = c, c R obteemos ua familia de rectas paralelas tal y como se observa e la Fig
116 (a) Superficie (b) Curvas de ivel Figura 5.2: Curvas de ivel de z = 4 x y Ejemplo 5.4 Aalizemos ahora las curvas de ivel del campo escalar defiido por z = x 2 + y 2 (Fig. 5.3). Debemos estudiar las curvas de ecuació x 2 + y 2 = c, c 0. (a) Superficie (b) Curvas de ivel Figura 5.3: Curvas de ivel de z = x 2 + y 2 05
117 Hemos cosiderado que c 0 porque es imposible que x 2 + y 2 sea egativo. Las curvas de ivel so circuferecias cetradas e el orige de coordeadas y de radio c si c > 0 y se reduce al orige de coordeadas si c = 0. Dibujar las gráficas de las fucioes de dos variables es e geeral ua tarea difícil. Dibujar la gráfica de ua fució de tres variables es secillamete imposible. Para dibujarlas ecesitaríamos u espacio de cuatro dimesioes; el propio domiio ha de ser ua porció del espacio tridimesioal. Lo que haremos es itetar represetar el comportamieto de ua fució f(x, y, z) de tres variables mediate las superficies de ivel de f que so ua geeralizació del cocepto de curva de ivel visto ateriormete. Las superficies de ivel de f(x, y, z) so los subcojutos del domiio co ecuacioes de la forma: f(x, y, z) = c, dode c es u valor e Im(f). Ejemplo 5.5 Cosideremos el campo escalar f(x, y, z) = x 2 + y 2 + z 2. Sus superficies de ivel x 2 + y 2 + z 2 = c 2, c R so esferas cocétricas cetradas e el orige de coordeadas; como se muestra e la Fig Figura 5.4: Superficies de ivel de x 2 + y 2 + z 2 06
118 Ejemplo 5.6 Si calculamos las superficies de ivel del campo escalar f(x, y, z) = Ax + By + Cz obteemos las superficies de ecuació Ax + By + Cz = c, c R que so plaos paralelos. Ejemplo 5.7 Vamos a calcular las superficies de ivel del campo escalar defiido como z f(x, y, z) x 2 + y 2 si (x, y, z) (0, 0, z), 0 si (x, y, z) = (0, 0, 0). Para ello, observamos que sólo toma valores o egativos y que o está defiida e los putos del eje z diferetes del orige. Teiedo e cueta que f sólo se aula cuado z = 0, la superficie de ivel cuado c = 0 es el plao xy. Para ecotrar las otras superficies de ivel, cosideramos c > 0 y hacemos f(x, y, z) = c. Etoces z x 2 + y 2 = c, y por tato z = c (x2 + y 2 ) que so paraboloides dobles de revolució (Fig. 5.5). Figura 5.5: Superficies de ivel de z x 2 + y 2 07
119 5.2. Fucioes vectoriales Ua fució f : D R R m co m > se llama ua fució vectorial de varias variables. Si = m >, la fució se llama campo vectorial. Ua fució vectorial f : D R R m se puede estudiar de forma atural por medio de m campos escalares f : D R R m x ( f (x),..., f m (x) ) si más que cosiderar las compoetes del vector f(x). Estos campos escalares se llama las fucioes compoetes de f. Por tato, ua fució vectorial o es más que u vector de m fucioes escalares: f = (f, f 2,..., f m ) Queda claro, además, que el domiio de ua fució vectorial debe estar coteido e la itersecció de los domiios de cada ua de sus compoetes. Ejemplo 5.8 Si cosideramos la fució vectorial de R 2 e R 3 defiida como f(x, y) = (x 2 + y, si x, x + e 2 ), las fucioes compoetes de f so: f (x, y) = x 2 + y f 2 (x, y) = si x f 3 (x, y) = x + e 2 E el caso de campos vectoriales, aú es posible idear ua represetació. Para campos vectoriales e el plao (o e el espacio) a cada puto (x, y) del domiio le correspode el vector (u, v) = f(x, y); basta dibujar dicho vector co orige e (x, y) para obteer ua represetació gráfica del campo. E la figura siguiete, Fig. 5.6, se ha represetado, co la ayuda de u programa iformático, el campo vectorial x f(x, y) = ( x 2 + y, y 2 x 2 + y ) 2 08
120 Figura 5.6: Campo vectorial 5.3. Límites y cotiuidad Imagiemos que, e u futuro, los cietíficos hallara ua fórmula (fució) que proporcioara la temperatura ambiete e cada istate t (medido e segudos) e u puto de la Tierra de coordeadas (θ, φ) (latitud y logitud, respectivamete). Dicha fórmula podría expresarse e la forma T = T (θ, φ, t) Etoces, podríamos predecir la temperatura ambiete e cualquier mometo de cualquier día del año. Sería de esperar, etoces, que dos putos espaciales próximos etre sí, tuviera temperaturas parecidas e el mismo istate o que el mismo lugar tuviera temperaturas próximas e istates cercaos. Más aú, cabe esperar que la temperatura o fuese muy distita e lugares próximos e istates cercaos (imagia el caos térmico si o fuera así). Este comportamieto de la fució T (θ, φ, t) es lo que llamaremos cotiuidad. Las fucioes cotiuas o requiere grades esfuerzos de imagiació; rige la mayoría de los procesos físicos y químicos (pero o todos!). Ates de abordar el cocepto de cotiuidad ecesitamos itroducir el de 09
121 límite de ua fució que os ayudará a eteder el cocepto de proximidad etre valores Límites La oció de distacia se preseta e la geometría euclídea al medir las logitudes de los segmetos que ue dos putos cualesquiera del espacio. A cotiuació se defie las distacias, tambié llamadas métricas, co las que trabajaremos usualmete. La aplicació d(x, y) := x y ; x, y R defie ua métrica sobre R, que, salvo que se diga lo cotrario, será la métrica usual de R. Aálogamete la aplicació d(z, z 2 ) := z z 2, z, z 2 C, será la métrica usual de C. La métrica euclídea sobre R será la defiida por d(x, y) := (x j y j ) 2 j= dode x = (x, x 2,..., x ) e y = (y, y 2,..., y ). El módulo o orma de u vector x = (x, x 2,..., x ) R se defie por x := x 2 j x = 2 + x x2 j= Por tato, se verifica que d(x, y) = x y. Si los subcojutos otables de R so los itervalos, sus equivaletes e R va a ser las bolas abiertas y bolas cerradas de cetro a y radio r > 0, defiidas como B r (a) = {x R : d(x, a) < r}, B r [a] = {x R : d(x, a) r} A cotiuació, se defie el diámetro de u cojuto A R, represetado por δ(a), como δ(a) = sup{d(x, y) : x, y A} 0
122 lo que permite defiir el cocepto de cojuto acotado como aquel cuyo diámetro es fiito o, equivaletemete, como aquel que está coteido e ua bola cerrada. E el estudio de los límites, y de las fucioes e geeral, es importate coocer o sólo el valor de la fució e u puto sio cómo se comporta dicha fució e los putos cercaos a él. Tiee setido etoces defiir etoro de u puto x R como u subcojuto U de R que cotiee ua bola abierta cetrada e x. Tambié se dice que x es iterior a U. Es decir, u etoro de x cotiee al puto x y a todos sus vecios. De especial iterés so los llamados cojutos abiertos defiidos como los subcojutos de R que so etoros de todos sus putos; es decir, co la propiedad A es u cojuto abierto de R sii x A r > 0 tal que B r (a) A. Cabe otar, etoces, que u cojuto A es abierto si, y solamete si, todos sus putos so iteriores. Tambié será de iterés coocer los putos frotera de u cojuto A defiidos como aquellos que cumple que cualquier bola cetrada e ellos cotiee putos del cojuto A y putos de su complemetario R \ A. El cojuto de putos frotera de A se deotará por A. Los cojutos abiertos, por tato, o cotiee putos frotera. Esta es la vetaja esecial de los cojutos abiertos; dado cualquier puto del cojuto abierto podemos acercaros a él desde cualquier direcció; es decir, todos sus vecios próximos está tambié e el abierto. Esta propiedad facilita muchas de las defiicioes que veremos a lo largo de este tema, y tambié de los siguietes, puesto que muchos coceptos está defiidos por límites y estos depede de que podamos acercaros cuato queramos al puto e cuestió. Por este motivo, e las disquisicioes teóricas se suele exigir que las fucioes esté defiidas e u abierto. A cotiuació se dará la defiició de límite para fucioes de dos variables, fácilmete geeralizable para fucioes de más variables. Esta defiició es, a su vez, ua geeralizació de lo que ocurre e fucioes de ua variable. Defiició 5.3 Sea f : D R 2 R, co D u cojuto abierto y sea (a, b) R 2. Se dice que λ R es el límite de f cuado (x, y) tiede a (a, b)
123 si ε > 0 δ > 0 / si (x, y) D y (x, y) (a, b) < δ f(x, y) λ < ε y se deota por lím f(x, y) = λ. (x,y) (a,b) E resume, la expresió aterior puede iterpretarse diciedo que el límite de f es λ si cuado (x, y) está cerca de (a, b) el valor de f(x, y) está cerca de λ. Ejemplo 5.9 Calcula el límite de f(x, y) = y 2 + 3xy cuado (x, y) tiede a (0, ). Solució: Dado que (x, y) tiede a (0, ), esto sigifica que x está cerca de 0 e y está cerca de, por lo que, ituitivamete, parece claro que f(x, y) = y 2 + 3xy estará cerca de =. Etoces, afirmamos que el límite será ; es decir, lím (x,y) (0,) (y2 + 3xy) = = Cabe otar que, e realidad, lo hecho ateriormete equivale a substituir x por 0 e y por y evaluar f(x, y). Nota: El procedimieto visto e el ejemplo aterior (substituir x por 0 e y por y evaluar f(x, y)) puede fucioar e muchos casos secillos pero o equivale siempre al cálculo del límite correcto. Igual que sucede e el cálculo de límites de fucioes de ua variable, la mayor dificultad se preseta cuado al efectuar estas operacioes el resultado es ua de las idetermiacioes típicas del cálculo de límites. Para resolverlas se utiliza técicas especiales que o abordaremos e este curso. A pesar de esto, coviee coocer alguos resultados que puede ayudaros a calcular ciertos límites. Teorema 5.4 (Criterio del Sadwich) Sea f, g, h : D R R verificado que g(x) f(x) h(x) x D 2
124 y sea a R. Si lím x a g(x) = lím x a h(x) = λ, etoces lím f(x) = λ x a Teorema 5.5 Sea f, g : D R R y sea a R, verificado que f(x) = 0 y g(x) es ua fució acotada e D. Etoces, lím x a lím (f(x)g(x)) = 0 x a El siguiete resultado relacioa el límite de fucioes y el límite de sucesioes; auque las sucesioes que aparece aquí está formadas por vectores de R. Teorema 5.6 Sea f(x) ua fució defiida e u etoro de x 0. Etoces, el lím f(x) existe y vale L si, y sólo si, para toda sucesió {x k } que coverge x x 0 a x 0, siedo x k x 0, para todo k; se cumple que lím f(x k) = L k + El siguiete ejemplo os muestra el iterés de este teorema: sirve para demostrar que ciertos límites o existe. ( ) Ejemplo 5.0 Calcula el lím si. x 0 x Solució: Vamos a ver que este límite o existe. Por el Teorema 5.6, basta ecotrar dos sucesioes {a } y {b } que coverja a 0 y que cumpla ( ) ( ) lím si lím si a Aprovecharemos, para ello, las propiedades de periodicidad de la fució seo. Sea, para cada, a = π b y b = π 2 + 2π Etoces, es claro que ambas coverge a 0 y, al evaluar la fució ( ) si = si(π) = 0, para todo a 3
125 ( por lo que lím si b a ) = 0; mietras que ( ) si = si( π 2 + 2π) = si π =, para todo 2 ( ) por lo que lím si b =, tal y como se quería demostrar. E la Fig. 5.7 se ha represetado la gráfica de la fució si ( ) x Figura 5.7: Gráfica de si( x ) Como puede observarse la fució oscila etre y al acercarse a x = 0; por lo que toma todos los valores posibles del itervalo [, ]. ( ) Ejercicio 5.2 Demuestra que o existe lím si (x,y) (0,0) x 2 + y 2. (H: Cosidera sucesioes e R 2 de la forma (a, 0) y (b, 0)) Ejemplo 5. Calcula el valor de lím xy si (x,y) (0,0) ( 5 x 2 + y 2 Solució: Si itetamos resolver este límite siguiedo el procedimieto del Ejemplo 5.9, ecotramos ua dificultad que ates o aparecía. Las variables 4 ).
126 x e y está ambas cerca de 0, por lo que el factor xy estará cercao a 0. 5 Si embargo, el valor de la expresió tiede a ifiito, al estar el x 2 +y 2 deomiador cercao a 0 y el seo de esta expresió o se acerca a igú valor cocreto, por lo que la técica de substituir x e y por 0 o es aplicable e este caso. No obstate, ( si es) cierto que, idepedietemete, del valor de x e y la fució si 5 se ecuetra acotada (e valor absoluto) por ; por lo x 2 +y 2 que podemos aplicar el Teorema 5.5 y deducir que ( ) 5 lím xy si (x,y) (0,0) }{{} x 2 + y 2 = 0 0 }{{} acotada Para el caso de fucioes vectoriales, las fucioes compoetes permite reducir el estudio de límites al estudio de campos escalares. Defiició 5.7 Si f : D R R m es ua fució vectorial co compoetes f = (f, f 2,..., f m ), diremos que si lím f(x) = (l, l 2,..., l m ) x a lím f i(x) = l i para i =, 2,..., m. x a Fucioes cotiuas El cocepto de cotiuidad se defie, de uevo, como ua geeralizació del caso de fucioes de ua variable. Defiició 5.8 Sea f : D R R y x 0 D. Diremos que f es cotiua e x 0 si ɛ > 0 δ > 0 / si x D y d(x, x 0 ) < δ = f(x) f(x 0 ) < ɛ Si f es cotiua e cada puto x 0 D, diremos que f es cotiua e D y lo escribiremos f C(D) 5
127 Ua fució vectorial f : D R R m es cotiua e u puto x 0 R si todas sus fucioes compoetes so cotiuas e x 0. Ejemplo 5.2 Cosideremos la proyecció π j : R R co j, defiida por π j (x, x 2,..., x ) := x j Sea x = (x, x 2,..., x ), x 0 = (a, a 2,..., a ) y ɛ > 0. Tomado δ = ɛ, se cumple que si d(x, x 0 ) < δ, etoces al ser x j a j = x j a j 2 < x a x j a j x a 2 y como d(x, x 0 ) = x a x j a j x a 2 < δ cocluimos de las dos codicioes ateriores que x j a j < δ; es decir, π j (x, x 2,..., x ) π j (a, a 2,..., a ) = x j a j < δ = ɛ y como este razoamieto es válido para cualquier x 0 R, cocluimos que las proyeccioes π j so cotiuas e R para j =, 2,...,. Icluso e casos secillos como el del ejemplo aterior el estudio de la cotiuidad de ua fució a partir de la defiició puede ser bastate difícil. Afortuadamete, al igual que sucede e el caso de fucioes de ua variable, la defiició de cotiuidad es totalmete aáloga a la de límite tomado λ = f(x 0 ), por lo que el estudio de la cotiuidad se reduce al estudio de límites. Teorema 5.9 f es cotiua e u puto x 0 si se satisface las siguietes codicioes: a) f está defiida e x 0. b) Existe lím x x 0 f(x) = l. c) f(x 0 ) = l. Como cosecuecia, es fácil deducir las propiedades de las fucioes cotiuas, totalmete aálogas a las de los límites. 6
128 Teorema 5.0 (Álgebra de fucioes cotiuas) Si las fucioes f y g so cotiuas e x 0 D, tambié lo so la suma f + g y el producto por u escalar αf, α R; el producto f g y el cociete f g, siempre y cuado g(x 0) 0; Además, la composició de fucioes cotiuas es cotiua: f : D R R m } cotiua e x 0 D g : B R m R p = g f es cotiua e x cotiua e f(x 0 ) B 0 Las fucioes matemáticas elemetales so cotiuas e su domiio de defiició. Esto, juto co el hecho de que la composició de fucioes cotiuas es cotiua, permite razoar la cotiuidad de umerosas fucioes. Por ejemplo, Ejemplo 5.3 f(x, y, z) = x 2 yz x 2 + y 3 z 2 8 es cotiua e R 3 por ser productos y sumas de fucioes cotiuas. De hecho podemos escribir f e fució de las proyeccioes π j. f = (π ) 2 π 2 π 3 (π ) 2 + (π 2 ) 3 (π 3 ) 2 8 Podemos geeralizar este resultado diciedo que toda fució poliómica de -variables es cotiua e R por ser producto y sumas de proyeccioes. Ejemplo 5.4 Razoa la cotiuidad de la fució f(x, y) = si(xy) e su domiio. Solució: La estrategia cosiste e razoar la cotiuidad de las diversas fucioes que compoe la fució f. Se sabe que la fució g(x, y) = xy es cotiua e R 2 por ser ua fució poliómica. La fució f es la composició de esta fució g y la fució elemetal seo (que so ambas cotiuas), por lo que la fució f es cotiua. Ejemplo 5.5 Razoa la cotiuidad de la fució f(x, y) = domiio. xy x 2 +y 2 e su 7
129 Solució: Se sabe que la fucioes xy y x 2 + y 2 so cotiuas e R 2 por ser fucioes poliómicas. La fució f es el cociete de ambas, por lo que la fució f es cotiua e todos los putos e los que el deomiador o se aula (que es, precisamete, su domiio). Ejercicio 5.3 Razoa la cotiuidad de las fucioes siguietes e su domiio:. f(x, y) = x 2 y 3xy g(x, y) = y 2 + x 2 y 2xy 2x 3 3. h(x, y) = ( x log + x 2 + y 2 + y ) x Ejercicio 5.4 Halla el domiio y razoa la cotiuidad e él de las fucioes: (a) f(x, y) = (x 2 y, si xy, 0) ( (b) f(x, y) = log( + x 2 + y 2 ), ) (x 2 + y 2 ) (Sol.: (a) D = R 2 ; (b) D = {(x, y) R 2 : x 2 + y 2 } (disco uidad) ) 5.4. Problemas adicioales Ejercicio 5.5 Sabiedo que x2 y 2 3 < arcta(xy) xy < ; qué puedes decir arcta(xy) sobre el valor de lím (x,y) (0,0) xy? (H: Aplica el Teorema 5.4) Ejercicio 5.6 Qué puedes decir sobre el valor de Aplica el Teorema 5.5) (Sol.: ) ( ) lím y si? (H: (x,y) (0,0) x (Sol.: 0 ) Ejercicio 5.7 Si f(x) es ua fució cotiua e x 0 y g(x) es ua fució discotiua e x 0, qué sucede co la suma f(x) + g(x)? (H: Aplica el Teorema 5.0) 8
130 Ejercicio 5.8 Si lím f(x, y) = L, es cierto que existe el valor (x,y) (x 0,y 0 ) f(x 0, y 0 )? Razoa la respuesta. y razoa su cotiui- Ejercicio 5.9 Halla el domiio de f(x, y) = x2 + y x y dad. (Sol.: D = {(x, y) R 2 : x y} ) ( ) 2 Ejercicio 5.0 Halla el domiio de f(x, y) = xy si y razoa su xy cotiuidad. (Sol.: D = {(x, y) R 2 : xy 0} ) Ejercicio 5. Halla el domiio de f(x, y, z) = l(x 2 + y 2 + z ) y razoa su cotiuidad. (Sol.: D = R 3 \ {(0, 0, 0)} ) Ejercicio 5.2 Razoa la cotiuidad de las siguietes fucioes: (a) f(x, y) = log( + x 2 + y 2 ) (b) f(x, y) = log ( x 2 xy + si(xy) log(x + y) ) 9
131 Tema 6 Fucioes difereciables Se sabe que la derivada y de ua fució de ua variable, y = f(x), puede iterpretarse como la tasa de variació de la variable y respecto de la variable x (es por eso que, frecuetemete, para remarcar este hecho, se utiliza la otació dy dx para represetar dicha derivada). Supogamos que teemos, ahora, ua fució de dos variables. Por ejemplo, la presió de u gas ideal como fució del volume y la temperatura del gas puede expresarse: P = ct V dode c es ua costate. Si estamos iteresados e coocer cómo varía la presió e fució del volume, a temperatura costate T 0, parece lógico calcular la derivada de P respecto de V supoiedo costate la temperatura, es decir, calcular la derivada de la secció trasversal de la fució P = f(v, T ) = ct V para T = T 0. E este tema se verá que este procedimieto ituitivo es perfectamete válido y que esta derivació parcial permitirá obteer u mejor coocimieto de las fucioes de varias variables. 20
132 6.. Derivadas parciales La derivada de ua fució de ua variable, f(x), e u puto x 0 se defie como f f(x 0 + h) f(x 0 ) (x 0 ) := lím h 0 h y dicho valor, si existe, represeta la pediete de la recta tagete a la curva y = f(x) e el puto (x 0, f(x 0 )). Como ya se ha dicho ates, tambié se utiliza la otació df dx (x 0). De forma similar, las derivadas parciales de ua fució f(x, y) se defie formalmete como límites: Defiició 6. Si f es u campo escalar de dos variables, las derivadas parciales de f e u puto (x 0, y 0 ) está defiidas como f x (x f(x 0 + h, y 0 ) f(x 0, y 0 ) 0, y 0 ) = lím h 0 h f y (x f(x 0, y 0 + h) f(x 0, y 0 ) 0, y 0 ) = lím h 0 h si estos límites tiee setido y existe. Observa que puede ocurrir que sólo exista ua de las derivadas parciales o ambas o igua. Tambié se suele utilizar la otació f x(x 0, y 0 ) = f x (x 0, y 0 ) y f y(x 0, y 0 ) = f y (x 0, y 0 ). La derivada parcial e u puto (x 0, y 0 ) es u úmero real. Cuado las derivadas parciales puede calcularse e putos geéricos (x, y) etoces estamos defiiedo ua ueva fució escalar, que se llama fució derivada parcial y que seguimos deotado por f f x (x, y) ( y (x, y), respectivamete). E ocasioes, prescidiremos del puto geérico y escribiremos, simplemete, f x ( f y, respectivamete). Esta derivada parcial coicide co ua derivació ordiaria (respecto de ua variable). Para verlo, cosidera la secció trasversal de f(x, y) para y = y 0 ; es decir, la fució f(x, y 0 ). Esta fució sólo depede de la variable x y podemos calcular la derivada de esta fució e x 0, obteiedo: d dx f(x, y f(x 0 + h, y 0 ) f(x 0, y 0 ) 0) = lím = f x = x 0 h 0 h x (x 0, y 0 ) es decir, que la derivada parcial de f respecto de x es la derivada de la secció trasversal de f correspodiete. Por tato, la derivada parcial puede 2
133 calcularse co las reglas de derivació ordiarias, supoiedo costate la variable y. Aálogamete, la derivada parcial de f respecto de y es la derivada de la secció trasversal de f para x = x 0. Por tato, la derivada parcial puede calcularse supoiedo costate la variable x. Ejemplo 6. Si f(x, y) = 5x 2 y si(x + y), podemos difereciar f co respecto a x, cosiderado y como ua costate, y obteemos f (x, y) = 0xy cos(x + y). x De maera similar, si cosideramos que x es costate y derivamos respecto a y, obteemos ua fució, f y (x, y) = 5x2 cos(x + y). Ejemplo 6.2 Calcula las derivadas parciales de la fució f(x, y) = x 7 y e x y. Solució: E este caso podemos calcular las derivadas parciales e cualquier puto (x, y) por el procedimieto de supoer costate ua de las variables. Así pues, f x (x, y) = 7x6 y e x y f y (x, y) = x7 + e x y Ejercicio 6. Calcula las derivadas parciales de f(x, y) = x arcta(xy). (Sol.: f x (x, y) = xy + arcta(xy); f +x 2 y 2 y (x, y) = x2 ) +x 2 y 2 Ejercicio 6.2 Calcula las derivadas parciales de f(x, y) = x 3 e x x cos y. (Sol.: f x (x, y) = (x3 + 3x 2 ) e x cos y; f y (x, y) = x si y ) Igual que sucede e el caso de ua variable, hay ocasioes e que, teiedo e cueta la defiició de la fució, o podemos calcular las derivadas 22
134 parciales derivado respecto de ua variable y debemos calcularla aplicado la defiició, es decir, calculado los límites de la Defiició 6.. Veamos el siguiete ejemplo. Ejemplo 6.3 Estudia la existecia, y calcula e su caso, las derivadas parciales e el orige de la fució x si f(x, y) = x 2 + y 2 si (x, y) (0, 0) 0 si (x, y) = (0, 0) Solució: A diferecia del ejemplo aterior, e este caso o podemos derivar directamete la expresió x si x 2 para obteer las derivadas parciales + y2 e el orige porque dicha expresió o está defiida e el orige. No teemos más remedio que aplicar la defiició de derivada parcial para calcular las derivadas parciales buscadas. Comezaremos co la derivada parcial respecto a la variable x: f f(0 + h, 0) f(0, 0) h si (0, 0) = lím = lím h 2 x h 0 h h 0 h = lím h 0 si h 2. Ahora bie, este último límite o existe ( por qué?) y, por tato, o existe f (0, 0). x Calculamos ahora la derivada parcial respecto a la variable y: f f(0, 0 + h) f(0, 0) 0 si (0, 0) = lím = lím h 2 y h 0 h h 0 h = lím h 0 (0) = 0 Ejercicio 6.3 Calcula las derivadas parciales e el orige de la fució x 2 + y 2 g(x, y) = x 4 + y 4 si (x, y) (0, 0) 0 si (x, y) = (0, 0) (Sol.: No existe. ) 23
135 Ejercicio 6.4 Calcula las derivadas parciales e el orige de la fució xy si si y 0 m(x, y) = y 0 si y = 0 (Sol.: f f x (0, 0) = y (0, 0) = 0 ) Aalizaremos a cotiuació la itrepretació geométrica de las derivadas parciales. Cosidera la superficie de la Fig. 6.. Figura 6.: Iterpretació geométrica de la derivada parcial Hemos cortado la superficie z = f(x, y) co el plao y = y 0 paralelo al plao xz. El plao y = y 0 corta la superficie e ua curva, la secció trasversal y 0 de la superficie, es decir, f(x, y 0 ), que es la gráfica de la fució y, por tato, g(x) = f(x, y 0 ) g (x 0 ) = f x (x 0, y 0 ); es decir, f x (x 0, y 0 ) es la pediete de la secció trasversal y 0 de la superficie z = f(x, y) e el puto P (x 0, y 0, f(x 0, y 0 )). 24
136 De maera similar se puede razoar que f y (x 0, y 0 ) es la pediete de la secció trasversal x 0 de la superficie z = f(x, y) e el puto P (x 0, y 0, f(x 0, y 0 )). De forma aáloga es posible defiir las derivadas parciales para fucioes de tres o más variables, co la salvedad de que aumeta el úmero de derivadas parciales a calcular (tatas como variables). Así, si teemos ahora u campo escalar de tres variables, podemos cosiderar tres derivadas parciales, f x, f y, f z. Defiició 6.2 Si f es u campo escalar de tres variables, las derivadas parciales de f e u puto (x 0, y 0, z 0 ) so defiidas como f x (x f(x 0 + h, y 0, z 0 ) f(x 0, y 0, z 0 ) 0, y 0, z 0 ) = lím h 0 h f y (x f(x 0, y 0 + h, z 0 ) f(x 0, y 0, z 0 ) 0, y 0, z 0 ) = lím h 0 h f z (x f(x 0, y 0, z 0 + h) f(x 0, y 0, z 0 ) 0, y 0, z 0 ) = lím h 0 h si estos límites tiee setido y existe. Ejemplo 6.4 Calcula las derivadas parciales de f(x, y, z) = x 2 y yz 3. Solució: Supoiedo que y y z so costates y derivado respecto a x, obteemos f x (x 0, y 0, z 0 ) = 2xy. De forma similar teemos: f y (x 0, y 0, z 0 ) = x 2 z 3 f z (x 0, y 0, z 0 ) = 3yz 2 25
137 6... La diferecial E esta secció geeralizaremos el cocepto de difereciabilidad de fucioes de ua variable a campos escalares. Las derivadas parciales por sí mismo o cumple este objetivo porque ada más refleja el comportamieto de la fució e alguas direccioes particulares (las direccioes de los ejes de coordeadas). Defiició 6.3 Se dice que u campo escalar f : D R R, co D u cojuto abierto, es difereciable e x 0 D si existe u vector y R tal que f(x + h) f(x) = y h + o(h) dode o(h) es ua fució que satisface la codició o(h) lím h 0 h = 0. Cabe señalar que el vector y depede de x 0. No es muy difícil demostrar las dos propiedades siguietes: () Si f es u campo escalar difereciable e x = x 0, etoces el vector y es úico. (2) Si f es u campo escalar difereciable e x 0, etoces f es cotiuo e x 0. El vector y que aparece e la Defiició 6.3 recibe el ombre de gradiete de f e el puto x 0 y lo deotaremos por f(x 0 ) (e alguos textos tambié se usa la otació grad (f) para deotar el gradiete de f). Como veremos posteriormete, el gradiete juega u papel importate e las aplicacioes del cálculo diferecial de campos escalares. Lógicamete, calcularlo utilizado la defiició de fució difereciable suele ser complicado. El siguiete resultado os proporcioa ua forma alterativa de calcularlo que es la que usualmete utilizaremos. Teorema 6.4 (a) Si f es u campo escalar de variables, difereciable e el puto x 0, etoces ( f f(x 0 ) = (x 0 ), f (x 0 ),..., f ) (x 0 ) x x 2 x 26
138 (b) Si f es u campo escalar que tiee derivadas parciales cotiuas e el puto x 0, etoces f es difereciable e x 0. Es importate darse cueta de que el gradiete defie u campo vectorial: si f es difereciable e todos los putos de u subcojuto D de R, etoces queda defiido el campo vectorial f : D R R. Ua cosecuecia importate del Teorema 6.4 es que el cálculo del gradiete se reduce al cálculo de derivadas parciales. Ejemplo 6.5 Calcula el gradiete del campo escalar f(x, y) = x e y y e x. Solució: Las derivadas parciales de f so: f x (x, y) = ey y e x, f y (x, y) = x ey e x Las derivadas parciales so cotiuas e todo R 2 al ser producto y suma de fucioes cotiuas. Por tato, la fució f es difereciable. El gradiete es el campo vectorial defiido como f(x, y) = (e y y e x )i + (x e y e x )j Ejercicio 6.5 Calcula el gradiete del campo escalar f(x, y, z) = x si(πy)+ y cos(πz). Calcula f(0,, 2). (Sol.: f(x, y, z) = (si(πy), πx cos(πy) + cos(πz), πy si(πz)), f(0,, 2) = (0,, 0) ) Ejercicio 6.6 Calcula el gradiete del campo escalar f(x, y) = 2x 2 3xy + 4y 2 e el puto (2, 3). (Sol.: f(2, 3) = (, 8) ) Ejercicio 6.7 Calcula el gradiete del campo escalar f(x, y) = 2x(x y) e el puto (3, ). (Sol.: f(3, ) = 2 i j ) 27
139 Si volvemos a la Defiició 6.3, se llama diferecial de f a la expresió y h que allí aparece. Como y = f(x 0 ) podemos escribir la diferecial como f (x 0 ) h + f (x 0 ) h f (x 0 ) h x x 2 x Etoces, así como las derivadas parciales represeta la tasa de variació de la fució f respecto de ua de las variables; la diferecial puede iterpretarse como la tasa de variació total de ua fució, respecto de cada ua de sus variables. E efecto, como los valores h j represeta el icremeto de las variables x j, podemos reemplazarlos por la otació x j y, etoces, de dode f := f(x + x) f(x) = f(x) x + o( x) f x = f(x) x x + o( x) x y al tomar límites cuado x 0 se tiee df(x) = f(x) dx Por ejemplo, si H = f(x, y, z) etoces, dh = f f f dx + dy + x y z dz dode cada diferecial, dx, dy y dz, represeta las variació total de las variables x, y y z, respectivamete. Ejemplo 6.6 La fuerza de atracció gravitatoria etre dos cuerpos de masas M y m separados a ua distacia R, viee dada por la fórmula: F = G M m R 2 dode G es la costate de gravitació uiversal. Si la masa de uo de los cuerpos, M, aumeta u 3 % mietras que la otra masa, m, aumeta u 2 % y la distacia, R, que los separa tambié aumeta u 3 %; estima el cambio e la fuerza F. Solució: Sabemos que: df = F F F dm + dm + M m R dr 28
140 Como coocemos los cambios relativos (porcetajes), vamos a calcular tambié el cambio relativo e F. Así, dividiedo lo aterior por F : df F = F M dm F = + Gm R 2 dm G M m R 2 + F m dm + F GM R 2 dm G M m R 2 = dm M + dm m 2dR R F R dr F + 2GMmdR R 3 G M m R 2 = 0,03 + 0,02 2 0,03 = 0,0 Por lo que el cambio e F es de ua dismiució del %. Ejercicio 6.8 La deflecció y, e el cetro de ua placa circular suspedida por el borde y uiformemete cargada viee dada por y = Kwd4 t 3 dode w =carga total, d =diámetro de la placa, t = amplitud y K es ua costate. Calcula el cambio aproximado e el porcetaje de y si se aumeta w e u 3 %, se dismiuye d e u 2 % y se aumeta t e u 4 %. (Sol.: 7 % ) Ejercicio 6.9 Si se mezcla x moléculas-gramo de ácido sulfúrico co y de agua, el calor liberado viee dado por la fórmula F (x, y) =.786xy.798x + y cal. Si partimos de 5 moléculas-gramo de ácido y 4 de agua y se aumeta, respectivamete, a 5.0 y 4.04, cuáto calor adicioal se geera? (Sol.: 0.02 cal. ) Ejercicio 6.0 Segú la ley de Pouseuille, la resistecia al flujo de sagre que ofrece u vaso saguíeo cilídrico de radio r y logitud x es R = cx r 4 dode c es ua costate. Estimar la variació porcetual de R cuado x aumeta u 3 % y r decrece u 2 %. (Sol.: R aumeta u % ) 29
141 6..2. Plaos tagetes Supogamos ua superficie de ecuació z = f(x, y), co f ua fució difereciable e u puto (x 0, y 0 ). Sabemos que existe las derivadas parciales f x (x 0, y 0 ) y f y (x 0, y 0 ) y que represeta las pedietes de las rectas tagetes a las seccioes trasversales para y = y 0 y para x = x 0, respectivamete. Estas seccioes trasversales so curvas sobre la superficie z = f(x, y) que pasa por el puto P 0 (x 0, y 0, z 0 ), dode z 0 = f(x 0, y 0 ) (véase la Fig. 5.); por lo que se defie el plao tagete a la superficie e (x 0, y 0, z 0 ) como el plao que cotiee a las dos rectas tagetes mecioadas. Puesto que la itersecció de este plao co los plaos verticales x = x 0 e y = y 0 debe ser las rectas tagetes descritas, se puede deducir que ua ecuació del plao tagete vedrá dada por z z 0 = f x (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ) Por otra parte, veremos e la secció siguiete que cualquier otra curva e la superficie z = f(x, y) que pase por el puto P 0 cumplirá que su recta tagete está e este plao, lo que justifica el térmio plao tagete. Ejemplo 6.7 Calcula la ecuació del plao tagete a la gráfica de la fució f(x, y) = e xy e el puto (, 0, ). Solució: Segú hemos visto, la ecuació del plao tagete es z z 0 = f x (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ) Basta calcular las derivadas parciales: por lo que, la ecuació es f x (, 0) = y exy = 0 x =, y = 0 f y (, 0) = x exy = x =, y = 0 z = f (, 0) (x ) + f (, 0) (y 0) } x {{} y }{{} 0 30
142 es decir, z = + y. Ejercicio 6. Calcula la ecuació del plao tagete a la gráfica de la fució f(x, y) = x e xy e el puto (, 0, ). (Sol.: z = x + y ) Si observamos, de uevo, la Defiició 6.3, obteíamos f(x, y) = f(x 0, y 0 ) + f (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ) +o(h) }{{} L(x,y) siedo ahora h = (x x 0, y y 0 ), que puede iterpretarse como que la fució L(x, y) aproxima a f(x, y) para h suficietemete pequeño. Pero la gráfica de z = L(x, y) o es más que el plao tagete, por lo que acabamos de probar que si ua fució es difereciable e u puto (x 0, y 0 ), etoces el plao tagete es ua aproximació a la gráfica de la fució f(x, y) e el puto de tagecia. Ejemplo 6.8 Utiliza el Ejemplo 6.7 para calcular u valor aproximado de f(., 0.) siedo f(x, y) = e xy. Solució: Dado que el plao tagete era z = +y etoces, f(x, y) +y para putos cercaos a (, 0), por lo que (e ) f(., 0.) 0. = 0.9 Cuado las superficies viee dadas e la forma f(x, y, z) = 0 y o es posible, o bie resulta muy complicado, despejar z e fució de x e y, podemos aplicar el siguiete resultado para calcular el plao tagete. Teorema 6.5 E cada uo de los putos del domiio de f e los que f 0, el vector gradiete f es perpedicular a las curvas de ivel de f que pasa por el puto, si f es u campo escalar de dos variables, y a las superficies de ivel que pasa por el puto, si f es u campo escalar de tres variables. 3
143 Ejemplo 6.9 Para la fució f(x, y) = x 2 + y 2 las curvas de ivel so circuferecias cocétricas x 2 + y 2 = c. E cada uo de los putos (x, y)) (0, 0), el vector gradiete f(x, y) = 2xi + 2yj es perpedicular a las circuferecias ateriores (ver Fig. 6.2). E el orige, la curva de ivel se reduce a u puto y el gradiete es simplemete el vector (0, 0) Figura 6.2: El gradiete es perpedicular a las curvas de ivel Veremos ahora la aplicació del Teorema 6.5 a curvas co ecuacioes de la forma f(x, y) = c para calcular rectas tagetes y rectas ormales (perpediculares). Después lo aplicaremos de forma similar al caso de superficies para calcular plaos tagetes. Teiedo e cueta dicho teorema, si (x 0, y 0 ) es u puto de la curva de ivel C, f(x 0, y 0 ) es u vector ormal a la curva 32
144 C e el puto (x 0, y 0 ). Por tato, la recta que pasa por (x 0, y 0 ) y tiee como vector director el vector perpedicular a f(x 0, y 0 ) es la recta tagete. Por tato, u puto (x, y) está e la recta tagete si verifica la igualdad (x x 0, y y 0 ) f(x 0, y 0 ) = 0. Ejemplo 6.0 Ecuetra u vector ormal y u vector tagete a la curva del plao de ecuació x 2 + 2y 3 = xy + 4 e el puto (2, ). Ecuetra, además, las ecuacioes de la recta tagete y de la recta ormal a la curva e el puto (2, ). Solució: La idea cosiste e expresar la ecuació de la curva como ua curva de ivel y así poder aplicar el Teorema 6.5. Para ello basta observar que podemos escribir la ecuació como x 2 + 2y 3 xy = 4 y, etoces, llamado f(x, y) = x 2 + 2y 3 xy, la curva es precisamete la curva de ivel C : f(x, y) = 4. Notemos, además, que el puto (2, ) perteece a C. El gradiete de f es f(x, y) = (2x y)i + (6y 2 x)j y, por tato, el gradiete f((2, ), es u vector ormal a la curva e el puto (2, ). Dicho gradiete vale f(2, ) = 3i + 4j Coocemos por tato u puto de la recta ormal buscada (debe pasar por el puto (2, )) y u vector director f(2, ). La ecuació de la recta ormal es: es decir, y = 4 3 x 5 3. x 2 3 = y 4, Ecotremos ahora la ecuació de la recta tagete. Si (x, y) es u puto de la recta tagete, el vector (x 2, y ) es u vector tagete y, por tato, f(2, ) (x 2, y ) = 0 es decir, la recta tagete tiee por ecuació 3x + 4y 0 = 0. 33
145 Apliquemos ahora el Teorema 6.5 al caso de superficies. E este caso, la propiedad os dice que el plao tagete a ua superficie dada por la ecuació f(x, y, z) = c e el puto x 0 = (x 0, y 0, z 0 ) es el plao que pasa por (x 0, y 0, z 0 ) co vector ormal f(x 0 ). Por tato, u puto x está e el plao tagete e el puto x 0 si, y sólo si, f(x 0 ) (x x 0 ) = 0 que es la ecuació del plao tagete (ver Fig. 6.3). E forma implícita: f x (x 0, y 0, z 0 ) (x x 0 )+ f y (x 0, y 0, z 0 ) (y y 0 )+ f z (x 0, y 0, z 0 ) (z z 0 ) = 0 Figura 6.3: Plao tagete Si ahora queremos calcular la recta ormal a la superficie e el puto x 0 sólo hemos de teer e cueta que u vector director es el vector f(x 0 ) que es perpedicular a la superficie e el puto x 0. La ecuació cotiua de la recta ormal es x x 0 = y y 0 = z z 0 f x (x f 0) y (x f 0) z (x 0) 34
146 Ejemplo 6. Ecuetra la ecuació del plao tagete y de la recta ormal a la superficie de ecuació xy + yz + zx = e el puto (, 2, 3). Solució: Como ates, la estrategia es expresar la ecuació de la superficie como ua superficie de ivel. E este caso, basta observar que la ecuació dada puede escribirse como f(x, y, z) = para el campo escalar f(x, y, z) = xy + yz + zx. Teemos que f(, 2, 3) = (5, 4, 3), debe ser perpedicular a la superficie de ivel y, por tato, perpedicular al plao tagete a esa superficie, de dode la ecuació del plao tagete es 5(x ) + 4(y 2) + 3(z 3) = 0, que simplificada es 5x + 4y + 3z 22 = 0. La ecuació de la recta ormal es: x 5 = y 2 4 = z 3 3 Ejercicio 6.2 Ecuetra la ecuació de la recta tagete y de la recta ormal a la curva x 2 + xy + y 2 = 3 e P (, ). (Sol.: recta tagete: x + y + 2 = 0, recta ormal: x y = 0 ) Ejercicio 6.3 Ecuetra la ecuació de la recta tagete y de la recta ormal a 2x 3 x 2 y 2 = 3x y 7 e P (, 2). (Sol.: recta tagete: x y 3 = 0, recta ormal: x + y + = 0 ) Ejercicio 6.4 Ecuetra la ecuació del plao tagete y de la recta ormal a la superficie z = ( x 2 + y 2) 2 e P (,, 4). (Sol.: plao: 8x + 8y z 2 = 0, recta: x 8 = y 8 = z 4 ) Ejercicio 6.5 Ecuetra la ecuació del plao tagete y de la recta ormal a xy 2 + 2z 2 = 2 e P (, 2, 2). (Sol.: plao: x + y + 2z = 7, recta: x = y 2 = z 2 2. ) 35
147 6..3. Matriz Jacobiaa Ua fució vectorial f = (f, f 2,..., f m ) de variables se dirá difereciable e u puto x 0 de su domiio cuado cada compoete f j lo sea. Por lo visto ates, debe existir todas las derivadas parciales f j (x 0 ). Etoces, x k se llama matriz jacobiaa a la matriz (m ) f f f x x 2 x f 2 f 2 f J f (x 0 ) = x x 2 2 x. f m x. f m x 2. f m x dode todas las derivadas parciales está evaluadas e el puto x 0. Observa que e cada fila j se ecuetra el gradiete de la compoete f j. Ejemplo 6.2 Calcula la matriz jacobiaa del campo f(x, y) = (xy, x+y 2 ). Solució: Sólo debemos calcular las derivadas parciales de cada compoete. Así pues, ( ) y x J f (x, y) = 2y 6.2. Derivadas direccioales Las derivadas parciales so derivadas e la direcció de los ejes de coordeadas. La defiició de derivada parcial se puede geeralizar a cualquier direcció defiida por u vector u diferete de cero. Recordemos que u vector uitario es u vector de orma uo. Defiició 6.6 Para cada vector uitario u, el límite f u(x 0 ) = lím h 0 f(x + hu) f(x 0 ) h si tiee setido y existe, se deomia derivada direccioal de f e x 0 e la direcció u. 36
148 Como ya sabemos, las derivadas parciales de f represeta las tasas de variació de f e las direccioes de los ejes de coordeadas i, j y k. La derivada direccioal f u proporcioa la tasa de variació de f e la direcció de u. E la Fig. 6.4 se muestra la iterpretació geométrica de la derivada direccioal de ua fució de dos variables. Fijemos u puto (x, y) e el plao xy, y sea C la curva itersecció de la superficie z = f(x, y) y el plao s que cotiee el vector u y es perpedicular al plao xy. Etoces f u(x, y) es la pediete de la recta tagete T a la curva C e el puto (x, y, f(x, y)). Figura 6.4: Iterpretació geométrica de la derivada direccioal Nota: La defiició de derivada direccioal e la direcció u requiere que el vector u sea uitario. No obstate, podemos exteder la defiició a vectores arbitrarios o ulos: la derivada direccioal de f e x e la direcció de u vector o ulo w es f u(x) dode u = w es el vector uitario que w tiee la misma direcció que w. Teorema 6.7 Si f es difereciable e x, etoces f tiee derivada direccioal e x e cualquier direcció u, dode u es u vector uitario y, además, se verifica la igualdad f u(x) = f(x) u. 37
149 Ejercicio 6.6 Para los campos escalares de los Ejercicios 6.5, 6.6 y 6.7, calcula la derivada direccioal e las direccioes (0,, 2), (2, 3) y (3, ), respectivamete. (Sol.:, 52 3, 0 ) 5 3 Teiedo e cueta las propiedades del producto escalar, la igualdad puede escribirse como f u(x) = f(x) u. f u(x) = f(x) u = f(x) u cos θ dode θ es el águlo etre f(x) y u. Como cos θ, teemos que la derivada direccioal f u(x) será máxima cuado cos θ = ; es decir, cuado θ = 0 o, equivaletemete, cuado u aputa e la direcció y setido de f(x). Además, el valor máximo será f(x). Por otra parte, la derivada direccioal f u(x) será míima cuado cos θ = ; es decir, cuado θ = π o, equivaletemete, cuado u aputa e la direcció y setido de f(x). Además, el valor míimo será f(x). Ya que la derivada direccioal es la tasa de variació de la fució e la direcció u cosiderada, se acaba de demostrar el siguiete resultado: Teorema 6.8 Si f es ua fució difereciable e el puto x 0, etoces f tiee máximo crecimieto a partir del puto x 0 e el setido de su gradiete (y la tasa de variació es etoces f(x 0 ) ) y tiee máximo decrecimieto a partir del puto x 0 e el setido cotrario (y la tasa de variació es etoces f(x 0 ) ). Ejemplo 6.3 La temperatura e cada uo de los putos de ua placa metálica viee dada por la fució T (x, y) = e x cos y + e y cos x. (a) E qué direcció crece la temperatura más rápidamete a partir del puto (0, 0)? Cuál es la tasa de icremeto? (b) E qué direcció decrece más rápidamete la temperatura a partir de (0, 0)? 38
150 Solució: Basta aplicar el Teorema 6.8. Comecemos por calcular el gradiete de T : T (x, y) = (e x cos y e y si x) i + (e y cos x e x si y) j. (a) A partir de (0, 0) la temperatura crece más rápidamete e la direcció del gradiete T (0, 0) = i + j La tasa de variació es T (0, 0) = i + j = 2 (b) La temperatura decrece más rápidamete a partir de (0, 0) e la direcció de T (0, 0) = i j. Ejercicio 6.7 Dada la fució de desidad λ(x, y) = x2 3y 2, ecotrar la tasa de variació del cambio de desidad (a) e (, ) e la direcció e la que la desidad decrece más rápidamete; (b) e (, 2) e la direcció de i y (c) e (2, 2) alejádose del orige. (Sol.: (a) ; (b) 3 3 ; (c) 26 2 ) Derivadas parciales de orde superior Recordemos que las derivadas parciales de u campo escalar si existe e ua bola de cetro x 0 defie u uevo campo escalar y que, por tato, podemos calcular tambié sus derivadas parciales si se da las circustacias coveietes para su existecia. Estas derivadas parciales se deomia derivadas parciales de segudo orde y se deota de la siguiete maera: f x i x j (x) = 2 f x j x i (x) := x j ( f x i ) (x) E el caso particular de ser i = j se escribe 2 f x 2 i e lugar de 2 f x i x i. Fijémoos e el siguiete ejemplo: 39
151 Ejemplo 6.4 Calcula las derivadas parciales de segudo orde del campo escalar f(x, y) = x 3 y x 2 y 2. Solució: Calculamos primero las derivadas parciales f x (x, y) = 3x2 y 2xy 2 f y (x, y) = x3 2x 2 y Ahora, para calcular 2 f (x, y), sólo hemos de volver a derivar respecto a la x2 variable x: 2 f (x, y) = x2 x (3x2 y 2xy 2 ) = 6xy 2y 2 El procedimieto para calcular 2 f (x, y) es similar. Volvamos a derivar y2 respecto a la variable y: 2 f y 2 (x, y) = y (x3 2x 2 y) = 2x 2 El cálculo de las otras derivadas parciales de segudo orde se realiza de ua forma similar. Para calcular 2 f (x, y) derivamos respecto x la derivada x y parcial de f respecto a y. 2 f (x, y) = x y x (x3 2x 2 y) = x 2 4xy y, por último, para calcular 2 f (x, y) derivamos respecto a y la derivada y x parcial respecto a x de la fució f: 2 f y x (x, y) = y (3x2 y 2xy 2 ) = 3x 2 4xy 2 f E el ejemplo aterior hemos visto que las derivadas cruzadas (x, y) y x y 2 f (x, y) coicide. Este hecho o es casual. Si las derivadas parciales x y 40
152 de segudo orde existe e ua bola que cotiee al puto (x, y) y so cotiuas e el puto (x, y), etoces las derivadas parciales cruzadas coicide e el puto (x, y). La igualdad aterior es cosecuecia, por tato, del hecho de que el campo escalar f(x, y) = x 3 y x 2 y 2 satisface esta codició. Los campos escalares co los que trabajaremos a partir de ahora verificará siempre la codició aterior, por lo que sólo tedremos que calcular ua de las dos derivadas cruzadas. Las derivadas parciales segudas (como la derivada seguda e el caso de fucioes reales de variable real) se utilizará para estudiar si u campo escalar tiee extremos locales. Si f es u campo escalar co derivadas parciales de segudo orde cotiuas e ua bola abierta que cotiee al puto x 0, deotamos por H(x 0 ) la matriz Hessiaa de f e el puto x 0 defiida como H(x 0 ) = f x x f f x 2 x f. x x 2 f x 2 x 2 f. x x x 2 x f x x f x x 2 f x x dode todas las derivadas estaá evaluadas e x 0. Notemos que la matriz Hessiaa H(x 0 ) es ua matriz simétrica ya que las derivadas cruzadas coicide e el puto x 0 y, por tato, defie ua forma cuadrática. U razoamieto aálogo permite defiir las derivadas de tercer orde como las derivadas parciales de las derivadas de segudo orde. Se deotará por f 3 f x i x j x k (x) = (x) := ( 2 ) f (x) x k x j x i x k x j x i Ejemplo 6.5 Cosidérese f(x, y, z) = x 2 yz. Solució: Etoces, f z = x2 y 2 f x z = 2xy. 3 f y x z = 2x Además, 3 f z x 2 = 2y 4
153 y así sucesivamete. 3 f z x z = 0 Evidetemete, el proceso puede reiterarse, de forma que es posible defiir derivadas parciales de orde p mietras se pueda derivar las parciales de orde p. E geeral, si u campo escalar admite derivadas parciales hasta u orde p y todas so cotiuas, se dice que f es de clase C p. Además, cuado u campo escalar es de clase C p para cualquier orde p, se dice que es de clase C Regla de la cadea La llamada regla de la cadea se utiliza para derivar la composició de fucioes, al igual que sucede co las fucioes de ua variable. Teorema 6.9 Sea D R y D R m abiertos, f : D R m ua fució difereciable e x 0, co f(d) D y g : D R p difereciable e f(x 0 ). Etoces la composició g f es difereciable e x 0 y además, J g f (x 0 ) = J g (f(x 0 )) J f (x 0 ) A partir de él se deduce la regla de la cadea, que admite diversas versioes segú sea las fucioes ivolucradas. Por ejemplo, si se tiee ua fució u = f(x, y, z) y cada variable x, y, z es, a su vez, fució de ua variable t resulta que la fució u es, e realidad, ua fució de t y tiee setido calcular du dt (t 0) = f dx x dt + f dy y dt + f dz z dt dode las derivadas de f está evaluadas e (x(t 0 ), y(t 0 ), z(t 0 )) y las derivadas de x, y, z e t 0. Otro ejemplo ocurre cuado las variables x, y, z sea, a su vez, fucioes de varias variables: si u = f(x, y, z) y cada variable x, y, z es, a su vez, fució 42
154 de las variables s, t resulta que u t = f x x t + f y y t + f z z t dode cada derivada se evalúa e su correspodiete puto y, aálogamete para la otra derivada parcial. u s = f x co f ua fució difereciable. Cal- ( x 2 y 2 Ejemplo 6.6 Sea z = f x 2 + y 2 cula el valor de la expresió x s + f y ) x z x + y z y y s + f z z s Solució: Llamamos v = x2 y 2 x 2. Etoces, z = f(v) co v ua fució + y2 que depede de x e y. Aplicamos la regla de la cadea y obteemos Ahora, por lo que df dv = f (v), z x = df v dv x z y = df v dv y v x = 4xy 2 (x 2 + y 2 ) 2, v y = 4x2 y (x 2 + y 2 ) 2 x z x + y z y = xf 4xy 2 (v) (x 2 + y 2 ) 2 + yf 4x 2 y (v) (x 2 + y 2 ) 2 ( 4x = f 2 y 2 (v) (x 2 + y 2 ) 2 4x2 y 2 ) (x 2 + y 2 ) 2 = 0 Ejemplo 6.7 Sea z = f(y/x), dode f es ua fució derivable. Calcula el valor de la expresió x 2 2 z x 2 + 2xy 2 z x y + y2 2 z y 2 43
155 Solució: Llamamos s = y/x y, etoces, z = f(s). Ahora aplicado la regla de la cadea. z x = df s ds x = df y ds x 2 z y = df s ds y = df ds x Para hacer las derivadas segudas se debe teer e cueta que df ds depediedo de la variable s y, etoces, ( ) df = d2 f s x ds ds 2 x Así, y ( df ds ) = d2 f ds 2 s y 2 z x 2 = ( ) df y x ds x 2 + df 2y ds x 3 = d2 f ds 2 = d2 f ds 2 y x 2 y x 2 + df ds 2y x 3 = y2 x 4 s x d 2 f ds 2 + 2y x 3 y x 2 + df ds df ds 2y x 3 sigue 2 z y 2 = ( ) df y ds x = d2 f ds 2 s y x = x 2 d 2 f ds 2 Fialmete, 2 z x y = ( ) df x ds x + df ds = d2 f ds 2 y x 2 x + df ds x 2 x 2 2 z x 2 + 2xy 2 z x y + y2 2 z y 2 = x2 = d2 f ds 2 s x x + df ds x 2 = y d 2 f x 3 ds 2 x xy [ y 2 x 4 [ y x 3 + y 2 [ x 2 d 2 f ds 2 d 2 f ds 2 + 2y x 3 df ds x2 ] df ds d 2 f ds 2 x 2 ] = 0 ] df ds
156 Ejercicio 6.8 Determia df dt, mediate la regla de la cadea, e los siguietes casos: (a) f(x, y) = x 2 y 3 ; x = t 3, y = t 2 ; (b) f(x, y) = x 2 y y 2 x; x = cos t, y = si t. (Sol.: (a) 2t ; (b) 2 si t cos t(si t + cos t) + si 3 t + cos 3 t ) Ejercicio 6.9 Sea f(x, y) = 2 x2 y + g(u, v), siedo g : R 2 R, co u = e x cos y, v = l y. Calcula (a) f f x (x, y); (b) y (x, y) (H: Exprésalas e fució de g g u (u, v); v (u, v)). (Sol.: (a) xy + e x cos y g x2 u (u, v); (b) 2 ex si y g u (u, v) + g y v (u, v) ) 6.5. Problemas adicioales Ejercicio 6.20 Ecuetra la ecuació de la recta tagete y de la recta ormal a la curva x 3 + y 3 = 9 e P (, 2). (Sol.: recta tagete: x + 4y 9 = 0, recta ormal: 4x y 2 = 0 ) Ejercicio 6.2 Ecuetra la ecuació del plao tagete y de la recta ormal a la superficie x 3 + y 3 = 3xyz e P (, 2, 3 2 ). (Sol.: plao: 4x 5y + 4z = 0, recta: x 4 = y 2 5 = z ) Ejercicio 6.22 Halla la ecuació del plao tagete a la gráfica de z(x, y) defiida por x 2 z + y 2 z 2 + z 3 = e el puto (0, 0, ). (Sol.: z = ) ( ) x Ejercicio 6.23 Calcula el gradiete de la fució f(x, y, z) = z l e y (,, 2). Calcula la derivada direccioal de la fució f aterior e el puto (,, 2) y e la direcció del vector v = (,, ). (Sol.: f(,, 2) = (2, 2, 0); f v(,, 2) = 4 3 ) 45
157 E los ejercicios , ecuetra u vector que idique la direcció e la cual la fució dada aumeta más rápidamete e el puto idicado. Halla la razó de cambio máxima. Ejercicio 6.24 f(x, y) = e 2x si y; (0, π/4) (Sol.: 2i + ( 2/2)j, 5/2 ) Ejercicio 6.25 F (x, y, z) = x 2 + 4xz + 2yz 2 ; (, 2, ) (Sol.: 2i + 2j 4k, 2 6 ) E los ejercicios , obté u vector que idique la direcció e la cual la fució dada dismiuye más rápidamete e el puto idicado. Ecuetra la razó de cambio míima. Ejercicio 6.26 f(x, y) = ta (x 2 + y 2 ); ( π/6, π/6) (Sol.: 8 π/6i 8 π/6j, 8 π/3 ) Ejercicio 6.27 F (x, y, z) = xze y ; (6, 0, 9) (Sol.: 3 8 i 2j 2 3 k, 8328/24 ) Ejercicio 6.28 Cosidera ua placa rectagular. La temperatura e u puto (x, y) de la placa está dada por T (x, y) = 5 + 2x2 + y 2 x 2 + y 2. Determia la direcció e que u isecto debe ir, partiedo de (4, 2), para que se efríe lo más rápidamete posible. Calcula la tasa de variació máxima. (Sol.: ( 50, 2 ) 00 ; ) Ejercicio 6.29 U esquiador experto desea desceder por ua motaña lo más rápidamete posible. Supoiedo que el perfil de la motaña viee dado por la gráfica de la fució f(x, y) = x 3 y +2xy 2 +xy 2; calcula la direcció que debe tomar cuado se ecuetra e las coordeadas (,, 2). (Sol.: la que idica el vector ( 6, 6) ) 46
158 Ejercicio 6.30 Sea z = f(x 2 + y 2 ) co f ua fució de clase C 2. Calcula x z y y z x (Sol.: 0 ) ( x 2 y 2 ) Ejercicio 6.3 Sea z = f x 2 + y 2 co f ua fució difereciable. Calcula el valor de la expresió x z x + y z y (Sol.: 0 ) Ejercicio 6.32 Prueba que la fució f(x, y) = relació f x x (x, y) + f y y (x, y) = f(x, y) y2 cualquiera que sea la fució derivable ϕ(u). y ϕ(x 2 y 2 ) satisface la 47
159 Tema 7 Teoremas del cálculo diferecial E este capítulo se abordará alguos de los resultados más coocidos del cálculo diferecial que, e geeral, se correspode co geeralizacioes adecuadas de los clásicos teoremas del cálculo de ua variable: teorema del valor medio, teorema de Taylor, etc. Meció aparte merece, por el uso ecesario de varias variables e su formulació, el teorema de la fució implícita; resultado éste de mucha trascedecia tato para el estudio posterior de máximos y míimos de fucioes como el estudio, e cursos más avazados, de la teoría y resolució de ecuacioes difereciales. 7.. Teorema del valor medio El teorema del valor medio, e fucioes de ua variable, trata del problema de evaluar la diferecia f(x + t) f(x) estableciedo la coocida fórmula f(x + t) f(x) = f (c)t supoiedo la existecia de la derivada f y siedo c u puto del itervalo de extremos x y x + t. El problema de evaluar la diferecia f(x + h) f(x) para fucioes de varias variables, puede reducirse a u problema de fucioes de ua sola variable 48
160 itroduciedo ua variable adicioal t y cosiderado la fució auxiliar F (t) := f(x + th) f(x) mateiedo fijas las variables x y h. Etoces, coforme t varía de 0 a, el puto de coordeadas x + th recorre el segmeto rectilíeo que ue x co x + h. Supoiedo expresamete que las derivadas parciales so cotiuas y aplicado el Teorema del Valor Medio a F (t) e el itervalo [0, ], se obtiee F () F (0) = F (θ) dode 0 < θ <. Por otra parte, aplicado la regla de la cadea se obtiee F (t) = i= h i f x i (x + th) y, fialmete, si h = (h,..., h ), resulta f(x + h) f(x) = i= f x i (ξ)h i dode ξ es u puto del segmeto rectilíeo que ue x y x + h. Este razoamieto se resume e Teorema 7. Sea f : D R R ua fució co derivadas parciales cotiuas e D, siedo éste u cojuto abierto y covexo. Etoces para cada par de putos x, x + h D se verifica f(x + h) f(x) = i= f x i (ξ)h i dode ξ es u puto del segmeto rectilíeo que ue x y x + h. Ua aplicació de este teorema se da e el cálculo de errores. El problema a abordar cosiste e coocer cómo afecta al valor de ua fució, el error cometido e la determiació del valor de las variables. 49
161 Medició de errores E la mayoría de los casos, los resultados obteidos al utilizar aparatos de medida para evaluar determiadas magitudes cotiee errores propios de las medicioes aproximadas que se realiza. Aú e el caso de obteer medidas exactas, las operacioes llevadas a cabo por medio de ordeadores so simplemete aproximacioes. Esto es debido, fudametalmete, a la precisió fiita co que opera y almacea los datos. Si ã es u valor aproximado de ua catidad a, llamaremos error absoluto a la diferecia ɛ(a) = a ã Si ɛ(a) > 0 la aproximació es por defecto y si ɛ(a) < 0 la aproximació es por exceso. El error relativo de a se defie como ɛ r (a) = ɛ(a) a = a ã a, a 0 Esta expresió parece poco útil, porque e realidad a es ua catidad que se descooce. Por esta razó, cuado ɛ(a) ã, suele utilizarse la aproximació ɛ r (a) ɛ(a) ã E la práctica suele utilizarse cotas de estos errores. Ua cota del error absoluto de a es u úmero real positivo M tal que ɛ(a) M De u modo similar, ua cota del error relativo de a es u úmero real positivo N tal que ɛ r (a) N Propagació de errores Supogamos que teemos catidades (datos obteidos por medio de medicioes, cálculos, etc.) agrupadas e u vector x = (x, x 2,..., x ) R y sus correspodietes aproximacioes x = ( x, x 2,..., x ) R. Supogamos tambié que f es ua fució de varias variables difereciable e u 50
162 domiio bastate amplio f : R R x f(x) x f( x). Nuestro objetivo es coocer cómo se propaga los errores por medio de la fució f. Podemos pesar que la fució f es u algoritmo o simplemete u cojuto de operacioes aritméticas. El error absoluto que se produce al actuar f sobre x viee dado por ɛ(f(x)) = f(x) f( x) = f(x, x 2,..., x ) f(x ± ɛ(x ), x 2 ± ɛ(x 2 ),..., x ± ɛ(x )), y, aplicado el Teorema del Valor Medio, f(x, x 2,..., x ) f( x, x 2,..., x ) = i= f x i (ξ)(x i x i ) (7.) dode ξ = x + α( x x) i α (0, ). Por la cotiuidad de las derivadas parciales, se puede supoer que f (ξ) f ( x), i, y calculado x i x i valores absolutos, obteemos fialmete ua cota del error absoluto: ɛ(f(x)) f ( x) x i ɛ(x i) (7.2) i= Ejemplo 7. El volume de ua pirámide triagular (de base u triágulo equilátero) de altura h y de arista de la base a es: 3a 2 h V = 2 Al medir la arista de la base y la altura de la pirámide se ha obteido a = 24 ± 0,6 cm. y h = 95 ± 0,4 cm. Qué error máximo tedrá el cálculo del volume? Cuáto vale dicho volume? Solució: Los datos coocidos so las cotas de los errores absolutos ɛ a y ɛ h de las magitudes a y h, respectivamete; es decir, ɛ a 0,6; ɛ h 0,4 5
163 por lo que, aplicado la fórmula (7.2), el error absoluto del volume, ɛ V vedrá acotado por ɛ V V a ɛ a + V h ɛ h de dode 3ah ɛ V 6 ɛ 3a 2 a + 2 ɛ h y substituyedo los valores a = 24 y h = 95 se tiee El volume calculado sería de ɛ V , ,4 428,6 cm V = 3a 2 h 2 co u error máximo de 428,6 cm. 7898,5 cm Ejercicio 7. El área de u triágulo es ab si C dode a y b so las 2 logitudes de dos lados y C es el águlo compredido. Al medirlos se ha obteido que a = 50 ± 0,5, b = 200 ± 0,5 y C = 60 ± 2. Qué error tedrá el cálculo del área? (Sol.: 337,58; 25 % ) Ejercicio 7.2 El peso específico de u cuerpo viee dado por la fórmula s = A A W siedo A el peso e el aire y W el peso e el agua. Cual es el error máximo posible e el valor calculado de s si A = 9 ± 0,0 Kg. y W = 5 ± 0,02 Kg. Determia tambié el porcetaje máximo del error cometido. (Sol.: 0,043; 0,639 % ) Ejercicio 7.3 El pricipio de Arquímedes establece que cuado u cuerpo es sumergido e el agua, la diferecia etre los pesos del cuerpo e el aire y 52
164 e el agua es igual al volume del agua desplazada. Como cosecuecia, la desidad de u cuerpo puede calcularse mediate la fórmula s = m m m dode s es la desidad, m es el peso del cuerpo e el aire y m el peso del cuerpo e el agua (se trabaja co el sistema de uidades CGS, cetímetro gramo segudo). Si m = 00 ± 0,005 g. y m = 88 ± 0,008 g., ecotrar el valor de la desidad del cuerpo y el error máximo e la medida de la desidad s. (Sol.: s = 8,333 ± 0,0086 gr/cm 3 ) E ocasioes, se cooce cotas de los errores relativos e las medidas lo cual permite coocer, de uevo, ua cota del error relativo e la magitud calulada a partir de ellas. Ejemplo 7.2 La fuerza de atracció gravitatoria etre dos cuerpos de masas M y m separados a ua distacia R, viee dada por la fórmula: F = G M m R 2 dode G es la costate de gravitació uiversal. Si se cosidera que la masa de uo de los cuerpos (M) permaece costate, estima el error máximo e el cálculo de la fuerza F cuado m tiee u error máximo del 2 % y la distacia R del 3 %. Solució: Sea ɛ m, ɛ R y ɛ F los errores absolutos de las magitudes m, R y F, respectivamete. Etoces, se sabe que ɛ m m 0,02 y ɛ R R 0,03 Así, aplicado la fórmula (7.2), ɛ F F m ɛ m + F R ɛ R de dode ɛ F GM R 2 ɛ m + 2GMm R 3 ɛ R 53
165 y dividiedo por F = G Mm R 2 ɛ F F ɛ m m + 2 ɛ R 0, ,03 = 0,08 R y, por tato, el error máximo e F es del 8 %. Ejercicio 7.4 Co qué exactitud puede calcularse el volume de u cilidro circular recto, V = πr 2 h, a partir de medicioes de r y h que tiee u error máximo de %? (Sol.: 3 % ) Ejercicio 7.5 Si se quiere calcular el área de u rectágulo largo y estrecho a partir de las medicioes de la logitud y la altura, qué dimesió se ha de medir co más cuidado? Explica razoadamete la respuesta. (Sol.: logitud ) 7.2. Teorema de Taylor El teorema del Valor Medio proporcioa ua aproximació de primer orde, tambié llamada lieal, al valor de la diferecia f(x + h) f(x). E alguas ocasioes se ecesita aproximacioes de orde superior y el método para coseguirlo lo proporcioa los métodos de Taylor que permite el desarrollo de ua fució f(x) etoro a u puto x 0 hasta u cierto orde que depede, aturalmete, de la regularidad de la fució f. Para los propósitos de este curso baste euciar el desarrollo de segudo orde. Teorema 7.2 (Fórmula de Taylor de segudo orde) Si f es u campo escalar co derivadas parciales segudas cotiuas e ua bola abierta B r (x 0 ), etoces para todo h tal que x 0 + h B r (x 0 ) teemos f(x 0 + h) f(x 0 ) = f(x 0 ) h + 2 h H(x 0) h t + h 2 E x0 (h) dode H(x 0 ) es la matriz hessiaa de f e x 0 y E x0 (h) es ua fució que tiede a 0 cuado h 0. 54
166 Ejemplo 7.3 Expresa el poliomio p(x, y) = y 2 +3xy 2x 2 + e potecias de x e y +. Solució: Como se trata de u poliomio de segudo grado, basta aplicar el desarrollo de segudo orde a p(x, y) e el puto x 0 = (, ). Llamado h = (x, y + ), se tiee E primer lugar, p(x 0 + h) = p(x 0 ) + p(x 0 ) h + 2 h H(x 0) h t Ahora, las derivadas parciales, p x p y y las de segudo orde, p(, ) = 3 p = 3y 4x (, ) = 7 x p = 2y + 3x (, ) = x 2 p x 2 = 4 2 p x y = 3 2 p y 2 = 2 por tato, p(x, y) = 3 + ( 7, ) (x, y + ) + ( ) ( ) 4 3 x 2 (x, y + ) 3 2 y + y, operado, p(x, y) = 3 7(x ) + (y + ) 2(x ) 2 + 3(x )(y + ) + (y + ) 2 Ejercicio 7.6 Expresa el poliomio p(x, y) = x 2 + y 2 e potecias de x e y. (Sol.: 2 + 2(x ) + 2(y ) + (x ) 2 + (y ) 2 ) 55
167 7.3. Teorema de la Fució Iversa Cuado se resuelve u sistema de ecuacioes lieales determiado, es posible expresarlo e forma matricial Ax = b y se sabe que la solució viee dada por x = A b. Cuado el sistema de ecuacioes es o lieal, ya o puede represetarse por ua matriz sio por u sistema de fucioes: F (x,..., x ) = b F 2 (x,..., x ) = b 2. F (x,..., x ) = b que, llamado F = (F, F 2,..., F ), puede escribirse abreviadamete F(x) = b E el caso de existir la fució iversa F, la solució vedrá dada por x = F (b). E este apartado veremos codicioes suficietes para que eso ocurra, preservado, además, dicha fució las propiedades de regularidad, cotiuidad y difereciabilidad, de la fució F. Empecemos recordado alguos coceptos básicos de las fucioes iversas: ua aplicació f : A B admite iversa si existe g : B A tal que f g = id B y g f = id A Si tal aplicació g existe, es úica y se llama la iversa de f, la cual se represeta por g = f. Puede comprobarse que f admite iversa si, y sólo si, f es biyectiva; es decir, elemetos distitos de A tiee imágees distitas e B (iyectividad) y cada elemeto de B es image (úica) de u elemeto de A (sobreyectividad). Defiició 7.3 Sea f : D R R co D u cojuto abierto. Se dice que f es localmete biyectiva e x 0 D si existe u etoro abierto de x 0, U, tal que f : U f(u) es biyectiva La fució f : f(u) U se llama iversa local de f e x 0. 56
168 A cotiuació se verá codicioes suficietes para garatizar la existecia de iversa local difereciable: Teorema 7.4 (Fució Iversa) Sea f : D R cojuto abierto y x 0 D tales que R co D u (i) f es de clase C e D (ii) Det (J f (x 0 )) 0 siedo J f (x 0 ) la matriz jacobiaa de f e x 0. Etoces, existe U y V etoros abiertos de x 0 y f(x 0 ), respectivamete, verificado. f : U V es biyectiva 2. f : V U es de clase C e V 3. J f (f(x)) = (J f (x)), x U Ejemplo 7.4 Sea f : R 2 R 2 defiida como f(x, y) = (e x cos y, e x si y). Sea (a, b) R 2. Vamos a comprobar las hipótesis del teorema de la fució iversa. (i) Comprobamos que las derivades parciales so fucioes cotiuas. f x (x, y) = ex cos y f f C (R 2 ) y (x, y) = ex si y f 2 x (x, y) = ex si y f 2 y (x, y) = ex cos y f 2 C (R 2 ) f C (R 2 ) (ii) J f (a, b) = ea cos b e a si b e a si b e a cos b = ea 0 y, aplicado el teorema aterior, existe U, V etoros abiertos de (a, b) y f(a, b), respectivamete, de maera que 57
169 . f : U V es biyectiva 2. f : V U es de clase C e V 3. J f (f(x, y)) = (J f (x, y)), (x, y) U Es decir, f admite iversa local e cada puto (a, b) R 2. No obstate, f o admite iversa global e R 2 porque f o es iyectiva e R 2 ya que f(x, y) = f(x, y + 2π) Ejercicio 7.7 Sea la fució f(x, y, z) = (e x, si(x + y), e z ). Prueba que f es localmete iversible e (0, 0, 0), pero o admite ua iversa e igú etoro de (0, 0, 0) que cotega a (0, π, 0) Teorema de la Fució Implícita Ocurre co frecuecia que determiadas magitudes físicas viee relacioadas etre sí por ua fórmula e la que o es posible despejar algua de ellas e fució de las otras; por ejemplo, las ecuacioes de estado de u gas de la termodiámica, que relacioa el volume V, la presió P y la temperatura T. Si embargo, cabe esperar que, fijado ua presió y ua temperatura determiadas, pueda calcularse el volume que ocupa el gas. Este ejemplo ilustra el cocepto de fució defiida implícitamete por ua ecuació, que se desarrolla a cotiuació. Ua ecuació de la forma y = f(x) se dice que defie explícitamete a y como fució de x. E realidad, toda ecuació puede iterpretarse como ua relació etre las variables (x, y): para cada valor de x puede ecotrarse u valor de y de forma que (x, y) verifica la relació dada. Para que esta relació sea etedida como ua fució hay que exigir la uicidad de la image y. Así pues, cuado se tiee ua ecuació de la forma F (x, y) = 0, se dice que defie implícitamete a y como fució de x, si para cada x existe u úico y de forma que (x, y) verifica F (x, y) = 0. Además, sería coveiete que las propiedades de F (cotiuidad, difereciabilidad,...) tambié las coserve la fució implícita, así defiida. 58
170 Se verá, a cotiuació, codicioes suficietes para garatizar la existecia de fució implícita e u etoro de u puto. Para dar la versió geeral del teorema, aplicable a u sistema de m ecuacioes co icógitas, será ecesario ates itroducir algua otació específica: Cosidérese ua ecuació de la forma F(z) = 0 dode la fució F está defiida F : D R p+q R q ; es decir, el sistema tiee más variables que ecuacioes. Se busca codicioes suficietes para que esta ecuació defia implícitamete q fucioes de p variables. Por comodidad se supodrá que se desea escribir las q últimas variables e fució de las p primeras. Para distiguirlas co claridad se represetará co letras distitas; es decir, se escribirá las variables de F como F(x, x 2,..., x p, y, y 2,..., y q ) = F(x, y) Además, si F = (F, F 2,..., F q ) y (a, b) D se deotará F F ( ) (a, b) (a, b) (F, F 2,..., F q ) y y q Det (a, b) =. (y, y 2,..., y q ).... F q F q (a, b) (a, b) y y q Teorema 7.5 (Fució Implícita) Sea F : D R p+q R q, co D u cojuto abierto, y (a, b) D tales que (i) F(a, b) = 0 (ii) F de clase C m e D (m ) ( ) (F, F 2,..., F q ) (iii) Det (a, b) 0 (y, y 2,..., y q ) Etoces, existe W R p, etoro abierto de a, y ua úica fució de p variables f : W R q, f = (f, f 2,..., f q ), verificado. f(a) = b 2. f es de clase C m e W 3. F(x, f (x), f 2 (x),..., f q (x)) = 0, x W 59
171 Notad que la codició (3) de la coclusió os dice que las variables y j puede idetificarse co las fucioes f j (x), j q, lo que equivale a decir que está defiidas implícitamete por el sistema de ecuacioes. Ejemplo 7.5 Sea El sistema F (x, y, z) = xy 2 2yz + z 3 8 F 2 (x, y, z) = x 2 + y 2 + z 2 + xy x + y + z F (x, y, z) = 0 F 2 (x, y, z) = 0 defie implícitamete a y y z como fucioes de x e u etoro del puto P (2, 2, 0). Solució: Se comprueba las hipótesis del teorema de la fució implícita: } (i) F (P ) = 2 ( 2) 2 8 = 0, F 2 (P ) = 2 2 +( 2) 2 +2 ( 2) 2+( 2) = 0. (ii) F, F 2 C (R 3 ), por ser fucioes poliómicas. (iii) (F, F 2 ) (y, z) (P ) 0: 2xy 2z 2y + 3z 2 2y + x + 2z + = (x,y,z)=(2, 2,0) 8 4 = 4 Etoces, existe u etoro abierto V R de x = 2, y ua úica fució f : V R 2, f = (f, f 2 ), verificado. f(2) = ( 2, 0) 2. f C (V ) 3. F (x, f (x), f 2 (x)) = 0 F 2 (x, f (x), f 2 (x)) = 0 } x V. Esta última codició permite, además, calcular las derivadas de f e x = 2 (derivació implícita): 60
172 Se sabe del apartado (3) aterior que xf 2 (x) 2f (x)f 2 (x) + f 3 2 (x) 8 = 0 x 2 + f 2 (x) + f 2 2 (x) + xf (x) x + f (x) + f 2 (x) = 0 x V. Derivado este sistema respecto de x se obtiee: f 2 (x) + 2xf (x)f (x) 2(f (x)f 2(x) + f (x)f 2 (x)) + 3f 2 2 (x)f 2 (x) = 0 2x + 2f (x)f (x) + 2f 2(x)f 2 (x) + f (x) + xf (x) + f (x) + f 2 (x) = 0 Particularizado para x = 2, se tiee f 2 (2) + 4f (2)f (2) 2(f (2)f 2(2) + f (2)f 2 (2)) + 3f 2 2 (2)f 2 (2) = f (2)f (2) + 2f 2(2)f 2 (2) + f (2) + 2f (2) + f (2) + f 2 (2) = 0 Y, teiedo e cueta el apartado () de la coclusió, se cooce los valores f (2) = 2 y f 2 (2) = 0, por lo que resulta el sistema: 4 8f (2) + 4f 2 (2) = 0 y, agrupado los térmios, 4 4f (2) 2 + 2f (2) + f (2) + f 2 (2) = 0 8f (2) + 4f 2 (2) = 4 f (2) + f 2 (2) = que es u sistema lieal cuya solució es: f (2) = 0 f 2(2) = Ejercicio 7.8 Demuestra que y cos x = 0 defie ua fució implícita difereciable y = ϕ(x) e u etoro de (0,0). Calcula ϕ (0). (Sol.: ϕ (0) = 0 ) Ejercicio 7.9 Comprueba que la ecuació x 2 + xy + y 3 = defie a y como fució implícita de x e u etoro de x =, e el cual toma el valor y = 2. Calcula las derivadas primera y seguda de y e x =. 6
173 (Sol.: y () = 4 3 ; y () = ) Ejercicio 7.0 Comprueba que la ecuació x 2 + y 2 + z 2 = 49 defie a z = φ(x, y) implícitamete e u etoro de (6, 3), tomado e ese puto el valor z = 2. Calcula el gradiete de φ e (6, 3). (Sol.: (3, 3 2 ) ) 7.5. Problemas adicioales Ejercicio 7. La hipoteusa de u triágulo rectágulo mide 5,4±0, cm. y uo de sus catetos 6,8 ± 0, cm. Co qué exactitud puede calcularse el otro cateto? (Sol.: error máximo de 0,6 cm ) Ejercicio 7.2 E u experimeto para determiar el valor de la aceleració g de la gravedad, se mide el tiempo t de caída, e segudos, de u cuerpo que se deja caer ua distacia fijada x partiedo del reposo. La fórmula utilizada es, etoces, g = 2x t 2 Si los aparatos de medida, permite establecer u error máximo para x del % y para t del 0,5 %. Cuál es el error máximo que cabe esperar e la determiació de g? (Sol.: 3 % ) Ejercicio 7.3 El mometo de iercia de ua varilla logitudial, de masa m y logitud h, respecto a u eje que pase por uo de sus extremos viee dado por la fórmula I = m h2 3 Determia el error máximo e el mometo de iercia de ua varilla si h = 4 ± 0, cm y m = 3 ± 0, gr. (Sol.:,333 gr.cm 2 ) 62
174 Ejercicio 7.4 Desarrolla la fució f(x, y) = x 2 + xy + y 2 e potecias de (x ) e (y 2) mediate el poliomio de Taylor. (Sol.: 7 + 4(x ) + 5(y 2) + (x ) 2 + (x )(y 2) + (y 2) 2 ) Ejercicio 7.5 Desarrolla la fució e 2x cos(y) e forma de poliomio de Taylor, hasta el segudo orde, e el puto (0, 0). (Sol.: f(x, y) + 2x + 4x 2 y 2 ) Ejercicio 7.6 Halla el poliomio de Taylor de segudo orde de la fució f(x, y) = e y si(x), e el puto (π, 0). Utilízalo para obteer u valor aproximado de f(3.4, 0.0) y compáralo co el valor obteido mediate la aproximació lieal del plao tagete. (Toma π = e los cálculos) Ejercicio 7.7 Sea la fució (Sol.: f(x, y) π x (x π)y; f(3.4, 0.0) = 0.006; 2 L(3.4, 0.0) = ) g : R 2 R 2 (x, y) (e x+y si y, e x+y cos y) E qué putos de R 2 admite g iversa local? Admite g iversa e R 2? (Sol.: Admite iversa local e cada puto de R 2, pero o admite iversa global. ) Ejercicio 7.8 Prueba que f(x, y) = (e x y, y + 2)) admite iversa difereciable e u etoro de (0, 0). Halla J f (, 2). ( ) (Sol.: ) 0 Ejercicio 7.9 Prueba que el sistema de ecuacioes } x cos y + y cos z + z cos x = π x 2 + y 2 + z 2 xy = π 2 defie implícitamete ua fució difereciable f(x) = (f (x), f 2 (x)) e u etoro del puto x = 0 de forma que f (0) = 0 y f 2 (0) = π. Calcula f (0) y f 2 (0). (Sol.: f (0) =, f 2 (0) = 0 ) 63
175 Ejercicio 7.20 Halla todos los posibles valores de z 0 para que la ecuació x 2 xz + z 2 + yz = 4 defia implícitamete a z como fució de x e y e u etoro del puto (, 3, z 0 ). Ejercicio 7.2 Cosidera el sistema de ecuacioes xy + xz + yz = } x + y + z 2 = 2 (Sol.: z 0 = y z 0 = 3 ) (a) Prueba que el sistema de ecuacioes defie implícitamete a y y z como fucioes de x e u etoro del puto (0,, ). (b) Sea G(x) = log(yz), dode y = y(x) y z = z(x) represeta las fucioes implícitas del apartado aterior. Halla el valor de G (0). (Sol.: (b) G (0) = 2 ) Ejercicio 7.22 Sea z(x, y) la fució defiida implícitamete por la ecuació x2 + y 2 + z 2 xy 2 + x 2 = 3 verificado que z(, ) = 2. Halla el valor del parámetro a R para que la derivada direccioal f y (a,a) (, ) = 2. (Sol.: a = ) Ejercicio 7.23 Sea f(x, y) la fució defiida implícitamete por las ecuacioes x si y + e u e v = } 0 e x+y v cos u = e u etoro del puto (x 0, y 0, u 0, v 0 ) = ( π, π, 0, 0). Demuestra que f admite iversa local difereciable e ( π, π) y calcula la matriz jacobiaa J f (0, 0). ( ) (Sol.: J f (0, 0) = π π ) Ejercicio 7.24 El volume V, la presió P y la temperatura T de u gas de Va der Waals esta relacioados por la fórmula ( ) RT P = α V β V 2 64
176 co α, β y R costates. Si el volume V es ua fució de P y de T demuestra que V T = RV 3 P V 3 + α(v 2β) Ejercicio 7.25 La ecuació de Dieterici del estado de u gas es P (V b) e a RV T = RT, dode P es la presió, V el volume y T la temperatura del gas e u istate determiado y siedo a, b y R costates. Demuestra la fórmula V ( T = R + a ) ( RT V T V b a ) V 2 65
177 Tema 8 Extremos La cuestió de determiar los máximos y míimos que alcaza ua fució es de gra importacia e muchos problemas de igeiería, ecoomía y ciecias e geeral. Cuado el problema puede reducirse a ua sola variable, coocemos métodos para resolverlo matemáticamete: se busca los valores que aula la derivada y se determia su comportamieto como máximo o míimo segú el valor que toma la derivada seguda. Cuado el úmero de variables es mayor, dispoemos de criterios parecidos que veremos e este capítulo y que, como de costumbre, geeraliza lo que ocurre e el caso de ua variable real. 8.. Extremos libres E esta secció estudiaremos cómo calcular los valores extremos de campos escalares defiidos e u cojuto abierto. Las defiicioes básicas so similares a las defiicioes de fucioes reales de variable real. Defiició 8. Sea f : D R R u campo escalar y x 0 u puto que perteece a ua bola coteida e D. Diremos que f tiee u máximo local e x 0 si f(x 0 ) f(x) para todo x perteeciete a ua cierta bola de cetro x 0 (ver Fig. 8.(a)). 66
178 Diremos que f tiee u míimo local e x 0 si f(x 0 ) f(x) para todo x perteeciete a ua cierta bola de cetro x 0 (ver Fig. 8.(b)). Como e el caso de las fucioes reales de variable real, hablaremos de valores extremos para referiros simultáeamete a los máximos locales y a los míimos locales. E el caso de fucioes reales de ua variable real sabemos que si la fució f tiee u extremo local e u puto x 0, etoces la derivada f (x 0 ) = 0 o o existe tal derivada. E el caso de campos escalares teemos u resultado similar. Teorema 8.2 Si u campo escalar f tiee u extremo local e x 0, etoces o bie f(x 0 ) = 0 (cuado f es difereciable e x 0 ) o bie f(x 0 ) o existe. Los putos e los que el gradiete se aula o o existe se deomia putos críticos. Por el teorema aterior so los úicos putos e los que u campo escalar puede teer u extremo local. Los putos e los que el gradiete se aula se deomia putos estacioarios. Llamaremos putos de esilladura a los putos estacioarios e los que la fució o tiee u extremo local (ver Fig. 8.(c)). Si x 0 es u puto estacioario de u campo escalar f, la fórmula de Taylor de segudo orde os dice que f(x 0 + h) f(x 0 ) = 2 h H(x 0) h t + h 2 E x0 (h) Podemos iterpretar esta igualdad como que el sigo de la diferecia f(x 0 + h) f(x 0 ) depede del sigo de la forma cuadrática H(x 0 ) cuado los putos x 0 y x 0 + h está suficietemete próximos. Por tato, la aturaleza del puto estacioario x 0 puede aalizarse clasificado la forma cuadrática asociada a la matriz Hessiaa H(x 0 ). Podemos utilizar, pues, los criterios de clasificació de formas cuadráticas para estudiar si el puto estacioario x 0 es u máximo local, u míimo local o u puto de esilladura. Auque, como ya se ha dicho, se puede utilizar cualquier criterio de clasificació de formas cuadráticas, vamos a establecer uo de ellos que usa como 67
179 úica iformació las etradas e la matriz hessiaa. Para ello, empezamos co algo de otació. Dada ua matriz cuadrada H, a a 2 a a 2 a 22 a 2 H = a a 2 a etoces llamaremos meores pricipales de H, que represetaremos por H, H 2,..., H, a los determiates siguietes: H = a, H 2 = a a 2 a 2 a 22,..., H = det(h) Teorema 8.3 (Criterio de las derivadas parciales segudas) Supogamos que f tiee derivadas parciales de segudo orde cotiuas e ua bola que cotiee al puto estacioario x 0. Sea H la matriz hessiaa de la fució f e x 0. Etoces,. Si H j > 0,para todo j, etoces f alcaza u míimo local e x Si H j < 0 cuado j es impar y H j > 0 cuado j es par, etoces f alcaza u máximo local e x E otro caso, el criterio o clasifica. E el caso particular de fucioes de dos variables podemos afirmar u poco más. Teorema 8.4 Supogamos que f tiee derivadas parciales de segudo orde cotiuas e ua bola que cotiee el puto (x, y) el cual es u puto estacioario, es decir, f(x, y) = (0, 0). Sea A = 2 f (x, y), x2 B = 2 f (x, y), x y C = 2 f (x, y), y2 y sea D = AC B 2. Etoces, 68
180 (a) si D > 0 y A < 0, el puto (x, y) es u máximo local; (b) si D > 0 y A > 0, el puto (x, y) es u míimo local; (c) si D < 0, el puto (x, y) es u puto de esilladura. (Observa que, segú la otació del Teorema 8.3, A = H y D = H 2 por lo que la iformació adicioal que proporcioa este teorema es la clasificació de los putos de esilladura) (a) A < 0, D > 0 (b) A > 0, D > 0 (c) D < 0 Figura 8.: Tipos de extremos Ejemplo 8. Ecuetra los extremos locales del campo escalar dado por z = x 5 y + xy 5 + xy. 69
181 Solució: Comecemos por calcular los putos críticos, que so la solució del sistema: f x (x, y) = y(5x4 + y 4 + ) = 0 f y (x, y) = x(5y4 + x 4 + ) = 0 Como los factores 5x 4 +y 4 + y 5y 4 +x 4 + so siempre positivos, deducimos que la úica solució es el puto (0, 0), que es el úico puto crítico de f. Calculemos ahora las derivadas de segudo orde: 2 z x 2 (x, y) = 20x3 y, 2 z x y (x, y) = 5x4 + 5y 4 +, 2 f y 2 (x, y) = 20xy3 ; y, al evaluarlas e el puto crítico: A = 0, B = y C = 0; por lo que, D = AC B 2 = y, segú el Teorema 8.4, z tiee u puto de esilladura e (0, 0) (ver Fig. 8.2). Figura 8.2: Gráfica de z = x 5 y + xy 5 + xy. Ejercicio 8. Ecuetra los extremos locales del siguiete campo escalar: f(x, y) = xye (x2 +y 2 )/2 70
182 (Sol.: Puto de esilladura e (0, 0); míimos locales e (, ) y (, ); máximos locales e (, ) y (, )) ) Ejercicio 8.2 Sea f(x, y) = x 2 2xy + y 2. Para f teemos que D = 0. Podrías decir si los putos críticos so máximos locales, míimos locales o putos de esilladura? (Sol.: Los putos críticos so míimos locales) ) Ejercicio 8.3 Clasifica los putos críticos del siguiete campo escalar: z = (x 2 + 3y 2 ) e x2 y 2 (Sol.: Míimo e (0, 0) y máximo e (0, ) y (0, ); putos de esilladura e (, 0) y (, 0)) ) Ejercicio 8.4 Clasifica los putos críticos del campo escalar f(x, y) = 2x 2 + y 2 xy 7y. (Sol.: Míimo local e (, 4).) ) 8.2. Extremos codicioados E la secció aterior hemos estudiado los extremos de fucioes defiidas e u abierto. Si embargo, e muchos problemas los extremos debe determiarse cuado las variables está sujetas a ua serie de restriccioes (que ya o costituye u cojuto abierto). Sea f : A R R co A abierto de R y sea X A. Se cosidera la restricció f : X R X x f(x) es decir, es la fució f al cosiderarla evaluada sólo e los putos del subcojuto X. Es evidete que los extremos locales de f será, e geeral, distitos de los de f X ; icluso tambié ocurrirá que o comparte siquiera los mismos putos críticos. El problema de determiar los extremos locales de f X se llama u problema de extremos codicioados, aludiedo al hecho de que las variables (x, x 2,..., x ) viee ligadas por la codició de perteecer a X. Para determiar codicioes aalíticas que garatice la 7
183 existecia de extremos codicioados, debe impoerse uas ciertas codicioes de regularidad tato para la fució f como para el cojuto X. E esta secció vamos a estudiar los extremos de fucioes sujetas a restriccioes de la forma X = {x R : g(x) = 0} dode g es ua fució de clase C p co m < compoetes; es decir, u sistema de m ecuacioes co icógitas pero siempre co meor úmero de ecuacioes que de icógitas. Así, e lo que sigue, f : A R R será ua fució de ua cierta clase C p e A y X será u cojuto de esa forma. Vamos a distiguir dos posibilidades para el cojuto de restriccioes X, segú podamos despejar o o m variables del sistema e fució de las m variables restates Método de reducció de variables Supoemos, pues, que teemos ua fució de variables f(x, x 2,..., x ) y queremos hallar los extremos de la fució f cuado las variables (x,..., x ) está ligadas por u sistema de m ecuacioes de la forma F(x) = 0. El método cosiste e despejar m variables e fució de las otras y substituirlas e la fució f, por lo que el problema se reducirá a u problema de extremos libres para ua fució de m variables. Veámoslo e u ejemplo. Ejemplo 8.2 Ua partícula de masa m está detro de ua caja de dimesioes x, y, z y tiee la eergía de estado ( E(x, y, z) = k2 8m x 2 + y 2 + ) z 2 dode k es ua costate física. Si el volume de la caja es de 8 dm 3, halla los valores de x, y, z que miimiza la eergía de estado. Solució: Dado que el volume de la caja viee dado por xyz = 8; se trata de resolver el problema de extremos codicioados: ( Mi. E(x, y, z) = k2 8m x 2 + y 2 + ) z 2 c.p. xyz = 8 72
184 y, subs- De la restricció, puede despejarse, por ejemplo la varibale z = 8 xy tituyedo e la fució E, el problema se reduce a ( Mi. E(x, y) = k2 8m x 2 + y 2 + x2 y 2 ) 64 Por tato, se reduce a u problema de extremos libres, e las variables x e y. Basta, pues, aplicar el procedimieto visto e al secció aterior. (a) Putos críticos. Se resuelve el sistema: E x = ( k2 8m E y = k2 8m ) 2x 2xy2 + = ) ( 2 y 3 + 2x2 y 64 = 0 2 x 3 = xy y 3 = x2 y = x4 y 2 64 = x 2 y 4 } Etoces, teiedo e cueta que x e y so dimesioes de ua caja y ha de ser positivas ambas: x 4 y 2 = x 2 y 4 x 2 = y 2 x = y Substituyedo e la primera ecuació: 64 = x 6 x = 6 64 = 2 de dode se obtiee el puto crítico: A(2, 2). (b) Clasificació. Se calcula la matriz hessiaa: 6 H = k2 x 4 + y2 32 8m xy 6 xy 6 6 y 4 + x2 32 y, substituyedo los valores e el puto crítico, 6 H = k m H = k2 2 8m
185 de dode, H = k2 8m 2 > 0 ( ) k 2 2 ( H 2 = 8m 4 ) 6 > 0 A es u míimo. Por tato, la solució es: las dimesioes que miimiza la eergía de estado so x = y = z = 2 dm. Ejercicio 8.5 Ua caja rectagular si tapa ha de teer u volume de 2 metros cúbicos. Ecotrar las dimesioes de la caja que proporcioa el área míima. (Sol.: Logitud: m.; acho: m.; altura: 3 3) ) Ejercicio 8.6 Demostrar que ua caja rectagular de volume dado tiee ua superficie míima cuado es u cubo Método de multiplicadores de Lagrage E el apartado aterior se ha visto que para ecotrar los extremos cuado las variables está sujetas a ua restricció, se utiliza el método de despejar ua variable de la ecuació; substituir e la fució origial y resolver el problema de extremos co ua variable meos. Si embargo, este método o siempre es factible e, icluso, puede llevaros a o obteer todas las solucioes posibles. De hecho, el despejar ua variable de ua ecuació cosiste e aplicar el teorema de la fució implícita visto e el Capítulo 7. Para obviar estas dificultades, vamos a ver otro método de calcular los extremos de ua fució, cuado las variables está ligadas por ua restricció e forma de ua ecuació o de u sistema de ecuacioes (pero siempre e úmero meor al de variables). Puede euciarse ahora ya la codició ecesaria, coocida como método de los multiplicadores de Lagrage Teorema 8.5 Sea f : A R R co A abierto de R y f C (A). Sea X = {x A : g(x) = 0}, co g = (g, g 2,..., g m ) de clase C y cumpliedo 74
186 que la matriz jacobiaa de g e cada puto del cojuto X tiee rago máximo. Sea x 0 X. Si f X tiee u extremo local e x 0, etoces existe m escalares λ, λ 2,..., λ m tales que el puto x 0 es puto crítico de L(x) := f(x) + λ g (x) + λ 2 g 2 (x) λ m g m (x) Itroduciedo los parámetros λ, λ 2,..., λ m como variables adicioales e la fució L aterior, se reduce el problema de determiar los putos críticos de f que cumple las restriccioes al problema de determiar los putos críticos de la fució lagragiaa L(x, λ, λ 2,..., λ m ) = f(x) + λ g (x) + λ 2 g 2 (x) λ m g m (x) Se eucia ahora la codició suficiete para saber si u puto estacioario es máximo o míimo. Como ates, esto depederá del sigo de la forma cuadrática dada por la matriz hessiaa, auque e este caso, al haber restriccioes, o sirve el estudio realizado e el caso de extremos libres y debe estudiarse el sigo de la forma cuadrática restrigida al llamado espacio tagete al cojuto de restriccioes X. Afortuadamete, la teoría de formas cuadráticas dispoe de métodos para mecaizar esta tarea tal y como se propoe e el teorema siguiete. Teorema 8.6 (Clasificació de los putos críticos) Sea la fució f : A R R co A abierto de R y f C 2 (A). Sea X A como e el teorema aterior, dode ahora g = (g, g 2,..., g m ) de clase C 2. Supógase determiados m escalares λ, λ 2,..., λ m tales que el puto x 0 es puto crítico de L(x) = f(x) + λ g (x) + λ 2 g 2 (x) λ m g m (x) Sea Q la matriz expresada por bloques como sigue: H J Q = J t 0 siedo H la hessiaa de L(x) e x 0 y J la jacobiaa de g e x 0. Sea el poliomio e α de grado m H αi J p(α) = J t 0 Etoces, 75
187 . Si todas las solucioes de p(α) = 0 so positivas, f X alcaza e x 0 u míimo local estricto. 2. Si todas las solucioes de p(α) = 0 so egativas, f X alcaza e x 0 u máximo local estricto. 3. E otro caso, el criterio o clasifica. Ejemplo 8.3 Ecuetra los extremos de la fució f(x, y) = x 2 y, co y > 0, que verifique 2x 2 + y 2 = 3 Solució: Se trata de u problema de extremos codicioados. Como parece complicado despejar ua variable de la ecuació 2x 2 + y 2 = 3, lo resolvemos aplicado el método de los multiplicadores de Lagrage: (a) Putos críticos. Se costruye la fució Lagragiaa L(x, y, λ) = x 2 y + λ(2x 2 + y 2 3) y se busca los putos críticos: L x = 2xy + 4λx = 0 L y = x 2 + 2λy = 0 L λ = 2x2 + y 2 3 = 0 De la primera ecuació: x(y + 2λ) = 0 x = 0 ó y = 2λ E el caso x = 0, sustituyedo e la tercera ecuació sale y 2 = 3 y = 3 (la solució y = 3 o se cosidera ya que y > 0) y, al sustituir este valor e la seguda, resulta λ = 0. Así, e este caso se tiee el puto crítico: A(0, 3), λ = 0 E el caso y = 2λ se sustituye e la seguda y se obtiee: x 2 4λ 2 = 0 x 2 = 4λ 2 76
188 y, al sustituir las dos codicioes e la tercera ecuació, resulta 8λ 2 + 4λ 2 = 3 λ 2 = 4 λ = ± 2 Como tiee que ser y > 0 e y = 2λ sólo puede ser la solució λ = 2 y, etoces, y = y el valor de x es x 2 = 4λ 2 = x = ± por lo que, e defiitiva, se tiee los putos críticos B(, ) λ = 2 C(, ) λ = 2 (b) Clasificació. Para clasificar los putos se calcula la matriz por bloques: 2y + 4λ 2x 4x Q = 2x 2λ 2y 4x 2y 0 Esta matriz correspode exactamete a la matriz hessiaa de L como fució de x, y y λ, separado los bloques respecto de x e y del multiplicador λ. Para el puto A(0, 3), λ = 0 Q = y, etoces, hay que calcular el determiate: 2 3 α α = 2(2 3 α) = 0 α = 2 3 > 0 A es u mí. Para el puto B(, ), λ = 2 Q =
189 y, etoces, hay que calcular el determiate: α α 2 = 32 6( α)+4α = 0 α = < 0 B és u máx. Para el puto C(, ), λ = 2 Q = y, etoces, hay que calcular el determiate: α α 2 = 32 6( α) + 4α = 0 α = < 0 por lo que f alcaza e C u máximo. Para fializar, veremos gráficamete el proceso realizado. E la Fig. 8.3(a) se ha represetado la superficie z = x 2 y y la curva sobre ella correspode a la image de los putos (x, y) del plao que cumple la restricció 2x 2 +y 2 = 3 (elipse). Para u mayor detalle, e la Fig. 8.3(b) se ha represetado sólo la parte gráfica correspodiete al octate positivo. La elipse del plao XY es la restricció 2x 2 + y 2 = 3 y la image de dichos putos dibuja ua curva sobre la gráfica de la fució z = x 2 y. (a) Gráfica completa (b) Gráfica e el octate positivo Figura 8.3: Gráfica de z = x 2 y 78
190 Fialmete, e la Fig. 8.4, se ha represetado úicamete la curva restricció, f X ; es decir, la fució f evaluada e los putos de la elipse 2x 2 +y 2 = 3 y se ha señalado los putos críticos hallados que como se observa, correspode a u míimo y dos máximos locales. Figura 8.4: Extremos de la fució restrigida E dicha Figura 8.4 se observa, además, otro máximo y dos míimos, que correspode a la regió y < 0, que ha sido excluidos del estudio. Ejercicio 8.7 Halla los extremos de la fució f(x, y) = x 2 + y 2, que verifica la restricció x 2 + 2y 2 = 2 (Sol.: Míimos e (0, ) y (0, ); máximos e ( 2, 0) y ( 2, 0). ) 8.3. Máximos y míimos absolutos Por último, haremos ua itroducció al estudio de la teoría de máximos y míimos absolutos (o globales). Recordaremos las defiicioes básicas: Defiició 8.7 Supogamos que f : D R es u campo escalar defiido e u subcojuto D de R. Diremos que f tiee u máximo absoluto 79
191 (respectivamete, u míimo absoluto) e x 0 D si f(x) f(x 0 ) (respectivamete, f(x) f(x 0 )) para todo x D. El siguiete resultado demuestra la existecia de extremos absolutos e u tipo especial de subcojutos de R. Recordemos que u subcojuto de R es acotado si existe ua bola que lo cotiee y que es cerrado si cotiee los putos de su frotera. Teorema 8.8 (Teorema de existecia de extremos absolutos) Sea D u subcojuto cerrado y acotado de R, y sea f : D R u campo escalar cotiuo. Etoces existe putos x 0 y x e los que f alcaza sus valores máximo y míimo, respectivamete. E geeral, el problema de ecotrar los extremos absolutos de u campo escalar es ua tarea ada secilla. Si cosideramos el domiio del campo escalar D como ua uió de su iterior it(d) y de su frotera, D, podemos dividir el problema de ecotrar los putos e los que u campo escalar alcaza sus extremos absolutos, e subproblemas dode aplicar los resultados de las seccioes precedetes, siempre y cuado su frotera pueda expresarse como u cojuto de restriccioes de la forma adecuada. Sea f ua fució cotiua defiida e ua regió D de R cerrada y acotada. Para localizar el máximo y el míimo absoluto de f e D seguiremos los siguietes pasos:. Localizar los putos críticos de f e D (problema de extremos libres). 2. Ecotrar los putos críticos de f cosiderada como ua fució defiida sólo e D (problema de extremos codicioados). 3. Calcular el valor de f e todos los putos críticos. 4. Comparar todos estos valores y seleccioar el mayor y el meor. Observa que e esta estrategia o será ecesario clasificar los putos críticos. Ejemplo 8.4 Ecotrar los valores máximo y míimo de la fució f(x, y) = x 2 + y 2 x y + e el círculo defiido por x 2 + y 2. Solució: Seguimos los pasos idicados. 80
192 () Putos críticos e el iterior del círculo x 2 + y 2 <. f (x, y) = 2x = 0 x f (x, y) = 2y = 0 y ( lo que implica que el puto A 2, ) es el úico puto crítico e el iterior 2 del círculo x 2 + y 2 <. (2) Putos críticos e la frotera x 2 + y 2 =. Es u problema de extremos codicioados. Como o podemos despejar igua variable de la restricció aplicamos el método de multiplicadores de Lagrage. Formamos la fució lagragiaa, L(x, y, λ) = x 2 + y 2 x y + + λ(x 2 + y 2 ) y calculamos sus putos críticos. L x = 2x + 2λx = 0 L y = 2y + 2λy = 0 L λ = x2 + y 2 = 0 y substituyedo e la tercera ecuació λ = 2x 2x λ = 2y 2y x 2 + x 2 = x = ± 2 x = y por tato, se obtiee los putos críticos B( , 2 ) y C( 2, 2 ). (3) Calculamos el valor de la fució f e los putos críticos hallados. f(a) = 2 f(b) = 2 2 f(c) = (4) Seleccioamos los putos e los que la fució alcaza el valor mayor y el valor meor. Comparado los valores del paso (3) teemos que f tiee u míimo absoluto e B ( ( 2, 2) y el máximo absoluto se alcaza e el puto ) C 2 2, 2 2. Los valores míimo y máximo que f alcaza so 2 y 2+ 2, respectivamete. 8
193 Ejercicio 8.8 Ecuetra los valores máximo y míimo que alcaza la fució f(x, y) = x 2 + xy + y 2 e el círculo uidad. (Sol.: 3 2 es el máximo absoluto y 0 es el míimo absoluto ) E el ejemplo aterior, la frotera del domiio estaba formada por ua úica curva (la circuferecia); si embargo puede ocurrir que la frotera de D esté formada por ua uió de diversas curvas (como, por ejemplo, la frotera de u cuadrado que está formada por sus cuatro lados). E este caso, el paso (3) implica que tedremos que calcular los putos críticos de tatas fucioes de variable real como curvas forma la frotera. Además, e el paso (4) deberemos añadir los putos dode se ue las diversas curvas que forma la frotera (vértices). Ejemplo 8.5 Cosidera ua placa delgada que tiee la forma del triágulo de vértices A(, 0), B(, ) y C(, ). Supoiedo que la temperatura e cada puto viee dada por la fució T (x, y) = x 2 xy + y 2, determia las temperaturas míima y máxima (absolutas) e la placa. Solució: La frotera del triágulo está formada por tres segmetos de recta. Empezamos hallado las ecuacioes de las tres rectas que forma los lados del triágulo, AB, AC y BC. Para cada recta, se ecesita u puto y u vector: AB { A(, 0) v = ( 2, ) x 2 = y x = 2y +. Como A y C tiee la misma coordeada x =, es fácil deducir que AC es ua recta vertical de ecuació: x =. Por último, como B y C tiee la misma coordeada y =, es fácil deducir que BC es ua recta horizotal de ecuació y =. E la Figura 8.5 se ha represetado el triágulo, idicado además los putos críticos que hallaremos a cotiuació. 82
194 Figura 8.5: Extremos e u recito triagular Como se trata de u problema de extremos absolutos e u recito co frotera (los lados del triágulo), dividiremos el problema e subproblemas: () Putos críticos e el iterior del triágulo. E este caso, es u problema de extremos libres y los putos críticos debe aular las derivades parciales de T : T x } = 2x y = 0 T y x = y = 0 = x + 2y = 0 Por tato, deberíamos obteer u puto crítico P 4 (0, 0), pero este puto o perteece al iterior del triágulo (ver Fig. 8.5) y, por ello, o se cosidera. (2) Putos críticos e el lado AB de ecuació x = 2y +. Substituyedo la restricció e T reducimos el problema a ecotrar los putos críticos de T (y) = (2y + ) 2 (2y + )y + y 2 = 3y 2 + 3y + y, etoces, al ser u problema de ua variable, T (y) = 6y + 3 = 0 y = 2 Por tato, teemos u put crítico P (0, ) (perteece al lado AB). 2 83
195 (3) Putos críticos e el lado AC de ecuació x =. Substituyedo la restricció e T reducimos el problema a ecotrar los putos críticos de T (y) = y + y 2 y, etoces, al ser u problema de ua variable, T (y) = 2y = 0 y = 2 Por tato, deberíamos obteer u puto crítico P 2 (, ), pero este puto o 2 perteece al lado AC (ver Fig. 8.5) y, por ello, o se cosidera. (4) Putos críticos e el lado BC de ecuació y =. Substituyedo la restricció e T reducimos el problema a ecotrar los putos críticos de T (x) = x 2 + x + y, etoces, al ser u problema de ua variable, T (x) = 2x + = 0 x = 2 Por tato, teemos u puto crítico P 3 (, ) (perteece al lado BC). 2 (5) Como la frotera es uió de varias curvas, debemos añadir a los putos críticos ateriores los putos de uió de las curvas (vértices del triágulo): A(, 0), B(, ) y C(, ). (6) Calculamos los valores de T e cada puto crítico. T (0, 2 ) = 4 T ( 2, ) = 7 4 T (0, ) = T (, ) = T (, ) = 3 Y, por tato, el míimo se alcaza e el puto (0, ), co ua temperatura de de grado y el máximo se alcaza e el vértice (, ) co ua 2 4 temperatura de 3 grados. 84
196 Ejercicio 8.9 Ecuetra el valor máximo y el valor míimo del campo escalar f(x, y) = xy 2x 3y e la regió triagular T = { (x, y) 0 x 4, 0 y 2x } (Sol.: El valor máximo es 0 y el valor míimo es 8 ) Ejercicio 8.0 Ecuetra los extremos absolutos del campo escalar f(x, y) = si x + cos y e el rectágulo R defiido por 0 x 2π, 0 y 2π. (Sol.: 2 es el míimo absoluto y 2 es el máximo absoluto ) 8.4. Problemas adicioales Ejercicio 8. Calcula los extremos de la fució f(x, y) = x 2 + xy + y 2 4 l x 0 l y (Sol.: míimo e (, 2) ) Ejercicio 8.2 Calcula los extremos relativos de la fució f(x, y, z) = x + y2 4x + z2 y + 2 z (Sol.: míimo e (/2,, ) ) Ejercicio 8.3 Calcula los extremos de la fució f(x, y) = x 2 + y 2, co x > 0 e y > 0, codicioados por log(x 2 ) + y 2 =. (Sol.: míimo e (, ) ) Ejercicio 8.4 Calcula los putos de la curva x 2 + y = cuya distacia al orige de coordeadas sea míima o máxima. (Sol.: máximo e (0, ); míimos e (± 2, ) ) Ejercicio 8.5 Halla los extremos de la fució f(x, y) = x + 2y codicioados por x 2 + y 2 = 5. (Sol.: máximo e (, 2); míimo e (, 2) ) Ejercicio 8.6 Halla los extremos de la fució f(x, y) = x 2 y, co y > 0, que verifica la restricció 2x 2 + y 2 = 3. 85
197 (Sol.: míimo e (0, 3); máximos e (±, ) ) { x + z Ejercicio 8.7 Halla el puto o putos de la curva 2 = 0 cuya x + y = distacia al puto (, 0, 0) sea míima. (Sol.: (0,, 0) ) Ejercicio 8.8 La presió e el iterior de u fluido viee descrita por la fució P (x, y, z) = xy + xz + yz. Calcula la presió máxima e los putos de la superficie 2x + 3y + z = 4 sumergida e dicho fluido. (Sol.: 2 ) Ejercicio 8.9 Cosidera la fució f(x, y, z) = log(xyz) defiida para x > 0, y > 0, z > 0. Halla los extremos relativos codicioados por xy + yz + zx = 3. (Sol.: máximo e (,, ) co valor 0 ) Ejercicio 8.20 Halla los extremos relativos de la fució f(x, y, z) = x 2 + y 2 + z 2 co x > 0, y > 0, z > 0, codicioados por { xy 2 + yx 2 = 6 x + y z = 0 (Sol.: míimo e (2, 2, 4) ) Ejercicio 8.2 Halla u puto de la esfera x 2 + y 2 + z 2 = 4 que maximice la fució 2x 2 + 2y 2 + z 2 xy defiida e el domiio x > 0 e y < 0. (Sol.: máximo e ( 2, 2, 0) ) Ejercicio 8.22 Ecuetra el valor máximo y el valor míimo (absolutos) del campo escalar f(x, y) = 4xy 2 x 2 y 2 xy 3 e la regió triagular de vértices A(0, 0), B(0, 6) y C(6, 0). (Sol.: El valor máximo es 4 y el valor míimo es 64 ) Ejercicio 8.23 Halla el puto del plao 3x 4y + 2z 32 = 0 que está más cerca del orige de coordeadas y calcula esa distacia míima. (Sol.: ( 32 9, 6 9, 32 9 ); 6 3 ) Ejercicio 8.24 Ecuetra los valores máximo y míimo de la fució defiida por f(x, y) = e la regió rectagular x 3, y 4. x 2 + y2 (Sol.: El valor máximo es 2 2 y el valor míimo es 5 ) 86
198 Tema 9 Itegració El cocepto de itegral defiida se desarrolló históricamete para calcular el área de regioes plaas acotadas por líeas curvas. Tomado como referecia iicial que el área del cuadrado que tiee lados de logitud l es igual a l 2, es muy secillo calcular el área de cualquier rectágulo y, recurriedo a la geometría elemetal, puede calcularse tabié el área de cualquier polígoo si lo dividimos e triágulos. La ecesidad de u método más sofisticado de calcular áreas aparece al itetar calcular la superficie de figuras acotadas por curvas. Por ejemplo, cómo calcular el área de u círculo, o de ua parábola? Uo de los logros más importates del Cálculo Itegral es el de proporcioar u método uificado y eficiete para la resolució de este tipo de problemas. El cocepto básico aquí es el de la itegral. Iicialmete, lo etederemos como ua expresió para calcular el área por medio de u límite. Cosideremos ua fució positiva y acotada f defiida e u itervalo [a, b]. Vamos a medir el área de la regió acotada por la curva y = f(x) y las rectas x = a, x = b, y = 0 (e la práctica, la fució f será cotiua casi siempre). El método cosiste e reemplazar la regió curvada que queremos medir por recitos cuya área es fácil de calcular y que aproxima tato como sea ecesario la regió. Para ello, cosideraremos dos tipos de recitos: los que está icluídos e el iterior de la regió curvada y los que la cotiee. Obteemos así valores que aproxima el área de iterés superior e iferiormete. Empezaremos co alguas defiicioes. 87
199 9.. Defiicioes básicas Defiició 9. Ua partició P de u itervalo [a, b] es u cojuto fiito de putos {x 0, x..., x } del itervalo tal que esta ordeados de forma creciete, es decir, a = x 0 < x <... < x < x = b. Cada uo de los subitervalos [x j, x j ] para j =, 2,... es u subitervalo de la partició. Si δ j = x j x j, la logitud del mayor subitervalo, δ(p ) = máx{δ j : j }, se llama orma de la partició. Defiimos ahora las recitos que aproxima el área superior e iferiormete. Defiició 9.2 Sea M j y m j el supremo y el ífimo respectivamete de los valores de f(x) e el iterval [x j, x j ]. Defiimos y S(f, P ) = s(f, P ) = M j δ j j= m j δ j Se tiee que la suma superior S(f, P ) es la suma de las áreas de rectágulos, de los que el j-ésimo tiee base [x j, x j ] y altura M j. La suma de estas áreas es mayor o igual que la del área R coteida etre la curva y = f(x) y las rectas x = a, x = b, y = 0. Aálogamete, la suma s(f, P ) es meor o igual que el área de R (ver Fig. 9.) j= (a) Suma iferior (b) Suma superior Figura 9.: Sumas superior e iferior 88
200 Si ahora t j es u valor arbitrario del itervalo [x j, x j ] (j =,..., ) y tomamos el cojuto T = {t,..., t }, la suma satisface que σ(f, P, T ) = f(t j )δ j j= s(f, P ) σ(f, P, T ) S(f, P ) E la Fig. 9.2 se ha costruido esta suma tomado como cojuto T los putos medios de cada subitervalo. Figura 9.2: Suma para los putos medios Nuestro objetivo es demostrar que si f es ua fució razoablemete buea (lo que icluye a las fucioes cotiuas y a las moótoas), las tres sumas ateriores tiede a u límite comú cuado δ(p ) tiede a 0. Este límite deotado por b a f(x)dx será la itegral de la fució f sobre el itervalo [a, b]. Si embargo, la operació de límite que acabamos de itroducir es muy complicada. Por ello, abordaremos iicialmete u proceso más secillo. 89
201 9... Itegral superior e iferior de Darboux Si M, m so el supremo e ífimo de f(x) e [a, b] y si, dada ua partició P, costruimos las sumas S(f, P ) y s(f, P ) como ates, de las desigualdades M m j y m j m (j =,..., ) se deduce que m(b a) s(f, P ) S(f, P ) M(b a). Así que el cojuto de los valores S(f, P ) está acotado iferiormete por m(b a) y, por tato, tiee ífimo deotado b a f(x)dx que se llama itegral superior de Darboux de la fució f. Aálogamete, los valores s(f, P ) está acotados superiormete por M(b a) y, por ello, tiee supremo deotado b a f(x)dx que se llama itegral iferior de Darboux de la fució f. Los teoremas que sigue demuestra que la itegral superior es siempre mayor o igual que la itegral iferior. Teorema 9.3 La itroducció de u uevo puto de divisió e ua partició P dismiuye el valor de S(f, P )y aumeta el valor de s(f, P ). Corolario 9.4 Si P y P 2 so dos particioes de [a, b] tales que P P 2 etoces S(f, P 2 ) S(f, P ) y s(f, P 2 ) s(f, P ). Si la partició P está icluída e la partició P 2, como e el corolario, se dice que P 2 refia a P. A partir de los dos resultados ateriores se demuestra Teorema 9.5 b a f(x)dx b a f(x)dx 90
202 La posibilidad de que la itegral superior sea mayor estrictamete que la iferior es real Ejemplo 9. La fució defiida por f(x) = f(x) = 0 si x es racioal si x es irracioal defiida e el itervalo [0, ] satisface que su itegral superior es igual a mietras que su itegral iferior es igual a 0. Defiició 9.6 Se dice que f es itegrable Riema cuado la itegral superior de f es igual a la itegral iferior Teorema de caracterizació Teorema 9.7 La fució f es itegrable e el itervalo [a, b] si, y sólo si, existe el límite de los valores cuado δ(p ) tiede a 0. σ(f, P, T ) Corolario 9.8 Ua fució f acotada e [a, b] es itegrable si, y sólo si, para todo ɛ > 0, existe ua partició P de [a, b] tal que S(f, P ) s(f, P ) < ɛ. Etoces es posible demostrar que ua amplia variedad de fucioes so itegrables; etre ellas destacaremos dos tipos. Teorema 9.9 Si f es cotiua e [a, b] etoces f es itegrable e [a, b]. Teorema 9.0 Si f es moótoa e [a, b] etoces f es itegrable e [a, b] Propiedades de la Itegral Reglas de itegració y Teorema del Valor Medio Teorema 9. Dada ua fució itegrable f e [a, b], se satisface las siguietes propiedades: 9
203 . b a (f(x) + g(x))dx = b a f(x)dx + b a g(x)dx 2. b a c f(x)dx = c b a f(x)dx 3. b a f(x)dx = c a f(x)dx + b c f(x)dx 4. f g b a f(x)dx b a g(x)dx 5. La fució f es itegrable y se satisface b a f(x)dx b f(x) dx Por comodidad de otació se adopta los siguietes coveios b a f(x)dx = a a a b a f(x)dx = 0 f(x)dx Teorema 9.2 (Teorema del Valor Medio) Si f es cotiua e [a, b] etoces existe u valor c [a, b] tal que b a f(x)dx = f(c)(b a) Fució itegral. Regla de Barrow. Supogamos e lo que sigue, y hasta que o se diga lo cotrario, que f es itegrable e [a, b] y escribamos F (x) = x a f(t)dt (a x b) La fució así defiida se llama fució itegral. Teorema 9.3 F es ua fució cotiua. 92
204 Teorema 9.4 (Teorema Fudametal del Cálculo) Si f es cotiua e el puto x [a, b] etoces F es difereciable e x y se satisface F (x) = f(x). Se dice que F es ua primitiva de f e [a, b] cuado F (x) = f(x) para x [a, b]. Teorema 9.5 Si f es cotiua e [a, b], etoces existe primitiva de f e [a, b]. Teorema 9.6 (Regla de Barrow) Si f es itegrable e [a, b] y F es ua primitiva de f e [a, b] etoces b a f(x)dx = F (b) F (a) El Teorema 9.4 demuestra la existecia de ua fució primitiva de f cuado ésta es cotiua. Se deduce de las propiedades de la derivada que si F y G so primitivas de f etoces F G es ua costate. Por lo tato, el cojuto de todas las primitivas de f está formado por todas las fucioes de la forma F + k, siedo F cualquier primitiva de f y k ua costate arbitraria. El cojuto de todas las fucioes primitivas de f se deota f(x)dx y se deomia itegral idefiida de f. La regla de Barrow proporcioa u procedimieto muy secillo para calcular la itegral (defiida) de ua fució cuado se cooce su itegral idefiida. Es por ello importate dispoer de métodos para hallar la itegral idefiida de ua fució. Veremos alguos de estos métodos e lo que sigue. Teorema 9.7 (Propiedades de las itegrales idefiidas) d. dx f(x)dx = f(x) 2. d dxf (x)dx = F (x) + k 3. [αf(x) + βg(x)]dx = α f(x)dx + β g(x)dx E la págia 244 puede cosultarse alguas itegrales idefiidas imediatas (las que proviee de la derivació de las fucioes matemáticas elemetales). Veamos alguos ejemplos. 93
205 Ejemplo 9.2 Calcula I = (x 2 3x + 5) dx. Solució: I = x 2 dx + 3x dx + 5 dx = x 2 dx 3 x dx + 5 dx = x x x + k Ejemplo 9.3 Calcula I = dx si 2 x cos 2 x. Solució: I = si 2 x+cos 2 x si 2 x cos 2 x dx = dx cos + x dx = ta x cot x + k. si 2 x Ejemplo 9.4 Calcula I = cos 2 xdx. Solució: Aplicado la fórmula trigoométrica de cos 2 x se tiee I = +cos 2x 2 dx que ya puede descompoerse e itegrales imediatas. Ejercicio 9. Calcula la itegral si 2 (x) dx (Sol.: x 2 4 si (2x) + k ) Ejercicio 9.2 Calcula las siguietes itegrales: (a) si(ax) cos(bx) dx (b) cos(ax)cos(bx) dx Ejercicio 9.3 Calcula las siguietes itegrales: (a b) cos((a+b)x)+(a+b) cos((b a)x) (Sol.: (a) + k; 2b 2 2a 2 (b a) si((b+a)x)+(b+a) si((b a)x) (b) + k ) 2b 2 2a 2 (a) ta 2 (x) dx (b) si 3 (x) cos 4 (x) dx (Sol.: (a) ta(x) x + k (b) 5 cos7 x 7 cos 5 x 35 + k ) 94
206 Itegració por partes y sustitució Teorema 9.8 (Itegració por partes) Sea f y g fucioes cotiuas e [a, b] tales que existe sus derivadas f, g, que so tambié cotiuas e [a, b], etoces b a f(x) g (x)dx + b Ejemplo 9.5 Veamos alguos ejemplos: () I = l x dx. a f (x) g(x)dx = f(b) g(b) f(a) g(a) Solució: Tomamos f(x) = l x y g (x) = e la fórmula de itegració por partes. Y, por tato, I = x l x dx = x l x x + k (2) I = x 3 si x dx. Solució: Se aplica itegració por partes varias veces, tomado siempre como fució f(x) la parte poliómica, hasta llegar a la itegral de ua fució trigoométrica. I = ( 3x 2 6 ) si (x) + ( 6x x 3) cos (x) + k (3) I = e ax si bx dx y J = e ax cos bx dx Solució: Se aplica itegració por partes a las dos itegrales y se obtiee u sistema lieal de dos ecuacioes co icógitas I y J, que se resuelve si mayor dificultad. I = eax (a si (bx) b cos (bx)) b 2 + a 2 + k; J = eax (b si (bx) + a cos (bx)) b 2 + a 2 + k 95
207 (4) I = e 2x si x dx. Solució: Se aplica itegració por partes dos veces y se despeja el valor de I de la expresió. Tambié podemos aprovechar la fórmula del ejemplo aterior tomado a = 2 y b = ; por lo que, I = e2x (2 si x cos x) 5 + k Ejercicio 9.4 Calcula la siguiete itegral l 2 (x) dx. (H: Toma f(x) = l 2 (x) y aplica itegració por partes) (Sol.: x ( l 2 (x) 2 l (x) + 2 ) + k ) Ejercicio 9.5 Halla la fórmula de reducció de I = x cos(ax) dx. (Sol.: x (ax si(ax)+ cos(ax)) a 2 ( ) a 2 I 2 ) Teorema 9.9 (Itegració por sustitució) Sea f ua fució cotiua e [a, b] y sea g ua fució cotiua de [c, d] a [a, b] tal que g(c) = a y g(d) = b, y existe la derivada de g e [c, d]. Etoces (f g) g es itegrable e [c, d] y d c f(g(s)) g (s)ds = Ejemplo 9.6 Veamos alguos ejemplos: () I = 6 x 2 dx, x [ 4, 4]. b a f(x)dx Solució: Se aplica el cambio x = 4 si t, t [ π 2, π 2 ], dx = 4 cos t; por lo que la itegral se trasforma e I = 6 si 2 t 4 cos tdt = 6 si 2 t cos tdt = 6 cos 2 tdt que ya sabemos resolver. Para deshacer el cambio, se tiee e cueta que si t = x 4 y, por tato cos t = x2 6. Ahora, I = 8t + 4 si(2t) = 8t + 8 si t cos t = 8 arcsi x 4 + 8x x k 96
208 (2) I = dx (arcsi x) 3, x [, ]. x2 Solució: Se aplica el cambio u = arcsi x, du = dx x ; por lo que la 2 itegral se trasforma e I = u 3 du = u 2 x) 2 + k = (arcsi + k 2 2 habiedo deshecho el cambio e el último paso. (3) I = x 2 x 7dx Solució: Se aplica el cambio x = t 2 + 7, dx = 2tdt; por lo que la itegral se trasforma e I = (t 2 + 7) 2 2t 2 dt = 2 ( 5t t t 3) + k 05 que ya es imediata al ser la itegral de u poliomio y, deshaciedo el cambio, t = x 7, queda I = 2 ( 5(x 7) 3 x t + 294(x 7) 2 x t + 75(x 7) x t ) + k 05 Ejercicio 9.6 Calcula las siguietes itegrales: (a) dx x 2 a ; (b) 2 dx x 2 + a 2. (H: Aplica el cambio t = x + x 2 ± a 2 y comprueba que dt = dx x 2 ± a 2 ) (Sol.: (a) l (x + ) x 2 a 2 ; (b) l (x + ) x 2 + a 2 ) A cotiuació se propoe alguos ejercicios más de los tipos vistos ateriormete. 97
209 Ejercicio 9.7 Calcula las siguietes itegrales: (a) dx x 2 + 6x + 0 ; (b) dx 9x ; (c) dx x 2 (a > 0). a2 (Sol.: (a) arcta ( ) 2x+6 arcta( 2 + k; (b) 3x 5 ) 5 + k; (c) l(x a) 2a l(x+a) 2a + k ) Ejercicio 9.8 Calcula las siguietes itegrales: (a) dx ; (b) 9 4x 2 dx 3 2x x 2. (Sol.: (a) arcsi ( ) ( x 3 + k; (b) arcsi 2x 2 ) 4 + k ) Ejercicio 9.9 Calcula las siguietes itegrales: (a) e x 3e 2x + e x dx; (b) ta 3 (x) + ta(x) 2 ta(x) (Sol.: (a) 4 l (e x + ) 3e x l(2 ta(x) ) + k; (b) 4 ta(x) 2 + k ) dx Ejercicio 9.0 Calcula las siguietes itegrales: (a) cos(x) cos(x) si 3 (x) + 2 cos 2 dx; (b) (x) si(x) a 2 + b 2 si(x) dx (Sol.: (a) l(si(x)) 2 l(si(x)2 2) 4 + k; (b) l(b2 si(x)+a 2 ) b 2 + k ) 9.3. Aplicacioes Veamos algua aplicacioes de la itegral al cálculo de áreas, volúmees y logitudes de curva. Áreas de superficies limitadas por curvas. El área limitada por la curva y = f(x) (siedo f 0) y las rectas x = a, x = b, y = 0 es b a f(x)dx. (9.a) 98
210 2. El área limitada por las curvas y = f(x), y = g(x) (siedo f g) y las rectas x = a, x = b es b a [f(x) g(x)]dx. Ejemplo 9.7 Ejemplos de aplicacioes al cálculo de áreas: (9.b) (a) Calcula el área de la regió S limitada por las rectas x = 0, x = 2, y las curvas y = x(x 2), y = x/2. Solució: Hallamos los putos de corte etre las gráficas, plateado para ello la ecuació x(x 2) = x/2 x(2x 5) = 0 cuyas solucioes so x = 0 y x = 5/2. E la Figura 9.3 se ha represetado la regió solicitada. Figura 9.3: Área etre dos curvas Como el recito está limitado por x = 2, el área solicitada es a(s) = 2 0 [ x 2 (x2 2x)]dx = 2 0 [ 5 2 x x2 ]dx = 7 3 (b) Calcula el área de la regió S limitada por las rectas x =, x = 2 y las curvas y = x, y = x 3 /4. 99
211 Solució: Hallamos los putos de corte etre las gráficas, plateado para ello la ecuació x = x 3 /4 x(x 2 4) = 0 cuyas solucioes so x = 0, x = 2 y x = 2. E la Figura 9.4 se ha represetado la regió solicitada. Figura 9.4: Área etre dos curvas que se corta Se observa que hay dos recitos, dode las gráficas ha itercambiado sus posicioes, así pues, el área solicitada es a(s) = 0 [ x3 4 x]dx [x x3 23 ]dx = 4 6 Ejercicio 9. Calcula el área de la regió limitada por el eje OX y las curvas y = si 3 (x), y = cos 3 (x) co 0 x π/2. (Sol.: 2(5 2 2) 3 2 Ejercicio 9.2 Calcula el área compredida etre las curvas y = 6x x 2 e y = x 2 2x. ) (Sol.: 64 3 ) Ejercicio 9.3 Calcula el área de la regió limitada por el eje OX, la recta x = y la curva y = x x
212 (Sol.: 3 ) Ejercicio 9.4 Calcula el área del domiio limitado por la elipse de ecuació x2 + y2 = (a, b > 0). a 2 b 2 (Sol.: πab ) Logitud de u arco de curva. Dada la curva defiida por la gráfica de la fució y = f(x), x [a, b], su logitud viee dada por la fórmula L = b a + f (x) 2 dx. (9.2a) 2. Si la curva viee dada e forma paramétrica } x = x(t) t [a, b] y = y(t) etoces su logitud viee dada por L = b a x (t) 2 + y (t) 2 dt (9.2b) 3. Si la curva está e el espacio y sus ecuacioes so x = x(t) y = y(t) t [a, b] z = z(t) etoces su logitud viee dada por L = b a x (t) 2 + y (t) 2 + z (t) 2 dt (9.2c) Ejemplo 9.8 Calcula la logitud del arco de parábola y 2 = 2px, desde el vértice hasta el puto (, 2p). 20
213 Solució: Represetado la curva e forma paramétrica obteemos } x = t2 2p 0 t 2p y = t de dode, aplicado la Fórmula (9.2b), L = 2p 0 p l = + t2 p 2 dt = ( p 2 +2p+ 2p 2 p [ t t 2π 2 + p 2 + p 2 l t + t 2 + p 2 p ) 2p p p 2π ] 2p 0 Ejercicio 9.5 Calcula la logitud de ua circuferecia de radio r por los dos métodos siguietes: (a) utilizado la parametrizació x(t) = r cos t, y(t) = r si t, co 0 t 2π y la Fórmula (9.2b); (b) utilizado la ecuació de la semicircuferecia superior, y = r 2 x 2 y la Fórmula (9.2a). (Sol.: 2πr ) Área y volume de ua superficie de revolució Si se tiee ua curva defiida por la gráfica de y = f(x), siedo f 0, x [a, b], y giramos dado ua vuelta completa alrededor del eje OX, etoces se egedra u cuerpo de revolució cuya área lateral es y cuyo volume es S = 2π b a V = π f(x) + f (x) 2 dx b a f(x) 2 dx. (9.3a) (9.3b) Ejemplo 9.9 Veamos alguos ejemplos de aplicació de estas fórmulas. (a) Evalúa el volume del sólido S formado por la rotació 2π radiaes de la cicloide x = a(t si t), y = a( cos t), 0 t 2π. 202
214 Figura 9.5: Sólido de revolució geerado por ua cicloide Solució: Cuado t varía de 0 a 2π, la variable x crece de 0 a 2πa. Por lo tato, aplicado la fórmula para hallar el volume de u sólido de revolució a la fució y = y(x), se obtiee v(s) = π 2πa 0 y(x) 2 dx haciedo el cambio de variable x = a(t si t), 0 t 2π, resulta v(s) = π 2π 0 [a( cos t)] 2 a( cos t)dt = 5π 2 a 3. (b) Calcula el área de ua esfera E de radio R. Solució: La esfera puede obteerse por la rotació 2π radiaes de la gráfica de la curva y = R 2 x 2, R x R. Aplicado la fórmula para el área de ua superficie de revolució, resulta R a(e) = 2π R 2 x 2 R + x2 R 2 dx = 2π x2 R R Rdx = 4πR
215 Ejercicio 9.6 Calcula el área lateral de u cilidro circular recto de radio a = 5 y altura h = 8 (H: el cilidro es u cuerpo de revolució). (Sol.: 80π ) Área de ua superficie defiida por medio de coordeadas polares Sea f ua fució o egativa defiida e el itervalo [a, b]. El cojuto de todos los putos de coordeadas polares (ρ, θ) que satisface ρ = f(θ) es la gráfica de f e coordeadas polares. La ecuació ρ = f(θ) es la ecuació polar de esa gráfica. Ejemplo 9.0 Vemos dos ejemplos de ecuacioes polares a cotiuació.. La circuferecia co cetro (0, 0) y radio se represeta por las ecuacioes x 2 + y 2 = (coordeadas cartesiaas) y ρ = (coordeadas polares). 2. La curva cuya ecuació e coordeadas cartesiaas es (x 2 + y 2 ) 3 = y 2 se represeta e coordeadas polares como ρ 6 = ρ 2 si 2 θ ρ 4 = si 2 θ ρ 2 = si θ ρ = si θ Si se tiee ua curva defiida por ua ecuació polar ρ = r(θ), siedo r o egativa y defiida para θ e u itervalo [a, b], etoces el área del domiio S ecerrado por la gráfica de la fució e el itervalo a θ b viee dado por la itegral a(s) = 2 b a r 2 (θ)dθ. (9.4) Ejemplo 9. Ejemplos de aplicacioes al cálculo de áreas:. Calcula el área de u sector circular de radio R y amplitud α < θ < β. Solució: a(s) = β 2 α R2 dθ = R2 2 (β α). 204
216 2. Calcula el área de la regió S limitada por la curva cuya ecuació polar es ρ = si θ. Solució: a(s) = π/2 2 0 si θdθ = 2(cos 0 cos π 2 ) = 2. Ejercicio 9.7 Hallar el área de u lazo de la rosa de cuatro hojas cuya ecuació e polares es r = 3 si(2θ), 0 θ 2π. (Sol.: 9π 8 ) 9.4. Problemas adicioales Ejercicio 9.8 Halla el área de la regió limitada por la curva y = x 3 + x 2 2x y el eje OX. (Sol.: 37 2 ) Ejercicio 9.9 Halla el área de la regió limitada por la curva y = x 3 3x + 8 y las rectas y = 3x, x = 3 y x = 0. (Sol.: 8 4 ) Ejercicio 9.20 Halla el área de la regió del plao compredida etre la curva y = + x 2 y la parábola 2y = x2. (Sol.: π 2 3 ) Ejercicio 9.2 Halla el área ecerrada por la recta y = z y la parábola y 2 = 2x + 6. (Sol.: 8. ) Ejercicio 9.22 Halla el área acotada por el eje x y por u arco de la cicloide x = r (t si t), y = r ( cos t), dode r > 0, y 0 t 2π (H: Aplica la Fórmula (9.a)). (Sol.: 3πr 2 ) 205
217 Ejercicio 9.23 Halla el valor de b para que la recta y = b divida el recito ecerrado por las curvas y = x 2 e y = 4 e dos regioes de igual área. (Sol.: b = 3 6 ) Ejercicio 9.24 U alambre delgado tiee la forma de la primera espiral de la hélice α(t) = (cos t, si t, t), t [0, 2π]. Halla su logitud. (Sol.: 2 2 π ) Ejercicio 9.25 Halla la logitud de la líea helicoidal cóica x = a e t cos t, y = a e t si t, z = a e t ; desde el puto A(0, 0, 0) al puto B(a, 0, a). (H: Al puto A le correspode u valor del parámetro t 0 = y al puto B el valor t = 0). (Sol.: a 3. ) Ejercicio 9.26 Halla el volume del sólido geerado al girar la regió ecerrada por la parábola y = x 2 y la recta y = x, alrededor del eje OX ua vuelta completa. (Sol.: 2π 5 ) 206
218 Tema 0 Itegrales dobles y triples Hasta ahora se ha calculado el área de figuras geométricas plaas elemetales: el rectágulo, el círculo, el trapecio, etc. Pero, cómo calcular el área de figuras o regulares? Ua buea aproximació puede ser la de dividir la zoa e pequeños rectágulos y sumar las áreas de cada uo de ellos: Figura 0.: Mallado para la aproximació del área Esta idea era la que subyacía e la costrucció de la itegral que vimos e el tema aterior y que os permitió calcular logitudes de curvas, áreas limitadas por curvas y volúmees de cuerpos de revolució. E este tema, se geeraliza el cocepto de itegral defiida a fucioes de dos o tres variables, obteiedo las llamadas itegrales de área o de volume, respectivamete. Esto os permitirá calcular el volume de cuerpos limitados por superficies, o ecesariamete de revolució. Tambié permitirá calcular áreas mediate itegrales dobles secillas que e el tema aterior resultaba algo más complicadas. Se empezará defiiedo la itegral sobre u rectágulo. 207
219 0.. Itegrales dobles sobre rectágulos Sea f(x, y) ua fució acotada sobre u rectágulo R = [a, b] [c, d]. Ua partició del rectágulo R so dos cojutos de putos {x j } j=0 e {y j} m j=0, satisfaciedo a = x 0 < x < x 2 <... < x = b c = y 0 < y < y 2 <... < y m = d es decir, P = P P 2, dode P y P 2 so particioes de [a, b] y [c, d], respectivamete. Se llama área de R a v(r) = (d c)(b a). Toda partició divide al rectágulo R e m subrectágulos R jk = [x j, x j ] [y k, y k ], j =,...,, k =,..., m como se observa e la Figura 0.2. Se llama orma de la partició P a P = máx{v(r jk ) : j =,..., ; k =,..., m} Figura 0.2: Ua partició del rectágulo R = [a, b] [c, d] Cosidérese cualquier puto c jk del rectágulo R jk y fórmese la suma S(f, P ) = m j=0 k=0 208 f(c jk )v(r jk )
220 llamada suma de Riema para f E la siguiete gráfica hemos represetado las sumas de Riema para la fució f(x, y) = x 2 + y 2 tomado como puto c jk el puto medio del rectágulo y el puto iferior del rectágulo (a) c jk como puto iferior (b) c jk como puto medio Figura 0.3: Sumas de Riema Defiició 0. Si la sucesió {S(f, P )} coverge a u límite S, cuado la orma de la partició tiede a 0, que es el mismo para cualquier elecció de c jk, etoces se dice que f es itegrable sobre R y se escribe R f(x, y)dxdy = lím m P 0 j=0 k=0 f(c jk )v(r jk ) A cotiuació se resume las propiedades más importates de las fucioes itegrables. Teorema 0.2 Sea f y g dos fucioes itegrables sobre u rectágulo R. Etoces 209
221 . (Liealidad) f + g es itegrable sobre R y (f(x, y) + g(x, y))dxdy = f(x, y)dxdy + R R R g(x, y)dxdy 2. (Homogeeidad) αf es itegrable sobre R, para todo α R, y αf(x, y)dxdy = α f(x, y)dxdy R 3. (Mootoía) Si f(x, y) g(x, y), para todo (x, y) R, etoces f(x, y)dxdy g(x, y)dxdy R 4. (Aditividad) Si R = P Q co P y Q dos rectágulos cuya itersecció es ua líea recta o u puto o vacía, etoces f(x, y)dxdy = f(x, y)dxdy + f(x, y)dxdy R 5. (Valor absoluto) f tambié es itegrable y se verifica f(x, y)dxdy f(x, y) dxdy R P U primer ejemplo de ua amplia clase de fucioes itegrables la proporcioa el siguiete teorema Teorema 0.3 Toda fució cotiua sobre u rectágulo cerrado R es itegrable R R R Q Auque la clase de las fucioes itegrables es mucho más amplia, el teorema aterior será suficiete e muchos casos prácticos. E geeral, las fucioes itegrables so aquellas que so cotiuas salvo e cojutos muy pequeños. Defiició 0.4 (Medida ula) U subcojuto de R tiee coteido ulo si, dado ɛ > 0, existe u úmero fiito de rectágulos que lo recubre y la suma de sus volúmees es meor que ɛ. 20
222 U subcojuto de R tiee medida ula si, dado ɛ > 0, existe ua sucesió (fiita o ifiita) de rectágulos, R, que lo recubre y cumpliedo. V (R ) < ɛ = El criterio geeral para saber qué fucioes so itegrables lo proporcioa el siguiete teorema Teorema 0.5 (Criterio de Lebesgue) Ua fució defiida e u rectágulo es itegrable Riema si, y sólo si, el cojuto de putos de discotiuidad de la fució tiee medida ula Cálculo de itegrales dobles El cálculo de ua itegral doble se realiza mediate el cálculo de dos itegrales iteradas, de acuerdo al siguiete teorema: Teorema 0.6 (Teorema de Fubii) Sea f ua fució itegrable sobre u rectágulo R = [a, b] [c, d].. Si para cada x [a, b], la secció trasversal f x (y) := f(x, y), y [c, d], es itegrable sobre [c, d], etoces la fució F (x) := d es itegrable sobre [a, b] y se verifica b f(x, y)dxdy = F (x)dx = R a c f x (y)dy b a ( d c ) f(x, y)dy dx 2. Si para cada y [c, d], la secció trasversal f y (x) := f(x, y), x [a, b], es itegrable sobre [a, b], etoces la fució G(y) := b es itegrable sobre [c, d] y se verifica d f(x, y)dxdy = G(y)dy = R c 2 a f y (x)dx d c ( b a ) f(x, y)dx dy
223 f(x,y) 0 f(x,y ) 0 a c d x = x 0 F(x ) 0 a y=y 0 b d G(y 0 ) b c Figura 0.4: El teorema de Fubii Corolario 0.7 Si f es cotiua sobre u rectágulo R = [a, b] [c, d], etoces b ( d ) d ( b ) f(x, y)dxdy = f(x, y)dy dx = f(x, y)dx dy R a c c a Ejemplo 0. Se desea calcular la itegral doble R x2 y dxdy siedo R = [, 2] [0, ]. Solució: Dado que la fució x 2 y es cotiua e R basta aplicar el Teorema de Fubii para obteer R x 2 ydxdy = = 2 2 ( 0 x 2 2 dx = ) x 2 ydy dx = [ x 3 6 ] x=2 2 ] y= [x 2 y2 dx 2 y=0 x= = = 7 6 Ejercicio 0. Cálculese la itegral aterior cambiado el orde de itegració. 22
224 0..2. Itegrales dobles sobre recitos acotados Para geeralizar el cocepto de itegral doble a recitos acotados se hace uso de la fució característica {, si x A A (x) = 0, si x / A dode A R 2. Si el cojuto A es acotado y verifica que su frotera tiee medida ula, etoces la fució característica es itegrable sobre cualquier rectágulo R que cotiee a A y, e este caso, existe a(a) := A (x, y)dxdy R que se llama la medida o área de A. El cojuto A se dice, etoces, medible. Etoces, dada ua fució itegrable sobre u rectágulo R A, se defie f(x, y)dxdy := A (x, y)f(x, y)dxdy A R E la figura siguiete puede verse gráficamete este proceso, dode F (x, y) = A (x, y)f(x, y): Gráfica de f(x,y) Gráfica de F(x,y) D D R Figura 0.5: Recito acotado y fució característica 23
225 Esta defiició permite exteder la itegració a recitos más geerales: aquellos que so medibles. Por tato, hay que recoocer los cojutos que so medibles. Para los objetivos de uestro curso basta aplicar, e geeral, el siguiete resultado: Teorema 0.8 La gráfica de ua fució cotiua tiee medida ula; es decir, si Φ(x) es ua fució cotiua defiida e u itervalo I, el cojuto tiee medida ula. A = {(x, y) : y = Φ(x); x I} E defiitiva, los cojutos cuya frotera está formada por gráficas de fucioes cotiuas so medibles. E particular, puede distiguirse dos tipos de recitos: Recitos de tipo I A = {(x, y) R 2 : a x b; g 2 (x) y g (x)} siedo g 2 (x), g (x) fucioes cotiuas e [a, b]. E este caso, ( b ) g (x) f(x, y)dxdy = f(x, y)dy dx A a g 2 (x) g (x) D g (x) D D g (x) g (x) 2 g (x) 2 g (x) a b a b a b Figura 0.6: Alguos domiios de tipo I Ejemplo 0.2 Se quiere calcular la itegral (x + 2y) dy dx D 24 2
226 dode D es la regió acotada por la parábolas y = 2x 2 e y = + x 2. Solució: E primer lugar, tras represetar gráficamete el domiio de itegració, trazamos ua recta vertical, L, que pase por el domiio D y marcamos los valores de la variables y por dode etra y sale la recta L, como puede verse e la siguiete figura y = x L y = 2 x Figura 0.7: Itegració sobre ua regió de tipo I La regió de itegració es, por tato, el domiio de tipo I: D = {(x, y)/ x ; 2x 2 y + x 2 )} Luego: D (x + 2y) dy dx = +x 2 2x 2 (x + 2y) dy dx Ejercicio 0.2 Calcula la itegral doble T xydxdy siedo T el recito limitado por el triágulo de vértices A(0, 0), B(2, 0) y C(, ), expresado T como u recito de tipo I. (Sol.: 3 ) Ejercicio 0.3 Calcula la itegral doble T x ydxdy siedo T el recito limitado por el triágulo de vértices A(, ), B(2, 4) i C(3, 3), expresado T como u recito de tipo I. 25
227 (Sol.: 4 3 ) Recitos de tipo II A = {(x, y) R 2 : c y d; h (y) x h 2 (y)} siedo h (y), h 2 (y) fucioes cotiuas e [c, d]. E este caso, A f(x, y)dxdy = d ( ) h2 (y) f(x, y)dx dy c h (y) d h (y) D h (y) 2 d h (y) D h (y) 2 d h (y) D c c c h (y) 2 Figura 0.8: Alguos domiios de tipo II Ejemplo 0.3 Calculemos la itegral xy dy dx dode D es la regió acotada por y = x y 2x + 6 = y 2. D Solució: Después de represetar gráficamete el domiio de itegració, trazamos ua recta horizotal, L, que pase por el domiio D y marcamos los valores de la variables x por dode etra y sale la recta L, como puede verse e la siguiete figura. 26
228 2 x = y / L x = y Figura 0.9: Itegració sobre ua regió de tipo II Luego el domiio de itegració es el domiio de tipo II: { 2 y 4 D y + x 2 (y2 6) Por tato: D xy dy dx = 4 2 (y2 6) 2 y+ xy dx dy = Ejercicio 0.4 Calcula la itegral doble T xydxdy siedo T el recito limitado por el triágulo de vértices A(0, 0), B(2, 0) y C(, ), expresado T como u recito de tipo II. Compara el resultado co el obteido e el Ejercicio 0.2. (Sol.: 3 ) Ejercicio 0.5 Calcula la itegral doble T (x y)dxdy siedo T el recito limitado por el triágulo de vértices A(, ), B(2, 4) i C(3, 3), expresado T como u recito de tipo II. Compara el resultado co el obteido e el Ejercicio 0.3. (Sol.: 4 3 ) Alguas regioes puede escribirse idistitamete como de tipo I o de tipo II. E estos casos, se elige aquella que resulte más fácil o más corta. E el siguiete ejemplo, se ha calculado ambas para que se pueda comparar los procedimietos. 27
229 Ejemplo 0.4 Se desea calcular la itegral doble T xydxdy siedo T el triágulo de vértices A(0, 0), B(, 0) y C(0, 2). Solució: El recito puede verse e la figura expresado como de tipo I o de tipo II C 2 C 2.5 y=2-2 x.5 x= x= 2-y 2 A y=0 B A B (a) Recito de tipo I (b) Recito de tipo II Figura 0.0: U triágulo como regió de tipo I y II 0 x Para ello, si se expresa T como ua regió de tipo I: T 0 y 2 2x y, etoces T xydxdy = = = ( 2 2x 0 0 ) xy dy dx = ) (2 2x)2 (x dx = 0 2 ] x= [x 2 + x4 2 4x x=0 = = 5 6 ] y=2 2x [x y2 dx 2 y=0 ( 2x + 2x 3 4x 2) dx
230 0 y 2 Si se expresa T como u recito de tipo II: T 0 x 2 y 2 y, etoces T xydxdy = 2 0 ( 2 y 2 0 xy dx ) dy =... = 5 6 Ejercicio 0.6 Calcula la itegral de la fució f(x, y) = x 2 y 2 sobre la regió R del primer cuadrate limitada por las hipérbolas equiláteras xy =, xy = 2 y las rectas y = x 2, y = 3x. (Sol.: 7 6 l 6 ) Ejercicio 0.7 Calcular el área de la regió del primer cuadrate limitada por las curvas xy = 2, xy = 4, y = x, y = 3x. (Sol.: l 3 u 2 (uidades al cuadrado) ) Cálculo de áreas Si se cosidera ua fució cotiua o egativa f(x, y) 0 defiida e u recito acotado medible A, etoces la itegral doble f(x, y) dxdy A tiee u sigificado geométrico claro: represeta el volume del sólido formado por el recito A como base, paredes laterales verticales y como superficie superior la gráfica de f(x, y). Este resultado permite que, e el caso de itegrar la fució costate sobre u recito medible A, se obtega el área de dicho recito (e realidad, se obtiee el volume de u prisma recto de base el recito A y altura que equivale uméricamete al área de A). Es decir; a(a) := dxdy A 29
231 Ejemplo 0.5 Vamos a utilizar esta propiedad para calcular el área compredida por la gráfica de las fucioes y = se(x) + e y = cos(x) + e el itervalo [ 3π 4, 5π 4 ]. Solució: Primer paso: U croquis Para represetar gráficamete el área que queremos calcular, hallaremos e primer lugar, los putos de iterseció de las dos fucioes que se ecuetra e ese itervalo, es decir, igualamos las dos fucioes y obteemos que: Luego los putos de itersecció so P = ( 3π 4, ), P 2 = ( π 4, se(x) + = cos(x) + se(x) = cos(x) x = 3π 4, π 4, 5π ), P 3 = ( 5π 2 4, 2 + ) Como podemos ver e la gráfica, Fig. 0. se obtiee dos domiios simétricos que tiee el mismo área. Es por ello que calcularemos el área que os pide multiplicado por dos el área de uo de los dos domiios coloreados e la gráfica y= cos(x) + y= se(x) + Figura 0.: Área etre dos gráficas Segudo Paso: Los límites de itegració e y Trazamos ua recta vertical, L, que pase por el domiio D y marcamos los valores de la variables y por dode etra y sale la recta L. Como puede verse e la Fig. 0., 220
232 esos valores so justamete los valores de las fucioes y = se(x) + e y = cos(x) +. Por lo tato el domiio D sobre el que teemos que itegrar es el domiio de tipo : D = {(x, y)/ π 4 x 5π 4 ; cos(x) + y se(x) + )} Tercer Paso: Cálculo de la itegral Aplicado la fórmula de itegració sobre domiios de tipo I a la fórmula de cálculo de áreas, tedremos que: Área(D) = da = 2 D =2 5π 4 π 4 5π 4 π 4 se(x)+ cos(x)+ 5π 4 dy dx = 2 π 4 se(x) cos(x) dx = 2 cos(x) se(x)] 5π 4 π 4 y] se(x)+ cos(x)+ dx = 4 2 Ejemplo 0.6 Calcular el área compredida por la gráfica de las fucioes y = x e y = (2 x) 2 y x = 0. Solució: Primer paso: U croquis Para represetar gráficamete el área que queremos calcular, hallaremos e primer lugar, los putos de iterseció de las fucioes que delimita el domiio a itegrar. Igualado las fucioes se tiee que: x = (2 x) 2 x 2 5x + 4 = 0 x = y x = 4 Luego los putos que delimita el domiio so P = (0, 0), P 2 = (, ), P 3 = (2, 0) 22
233 x= y x= 2 - y Figura 0.2: Área etre dos gráficas Segudo Paso: Los límites de itegració e x Trazamos ua recta horizotal que pase por el domiio D y marcamos los valores de la variable x por dode etra y sale la recta. Como puede verse e la Fig. 0.2 esos valores so y = x y x = 2 y. Por lo tato el domiio D sobre el que teemos que itegrar es el domiio de tipo II: D = {(x, y)/0 y ; y x 2 y} Tercer Paso: Cálculo de la itegral Aplicado la fórmula de itegració sobre domiios de tipo II a la fórmula de cálculo de áreas, tedremos que: ( ) 2 y Área(D) = da = dx dy = [x] x=2 y x=y dy D 0 y 0 [ ] y= = (2 y y dy = 2y 2 y3/2 3 y2 2) = y=0 Ejemplo 0.7. Cálculese el área del círculo uidad. Solució: Segú lo dicho a(c) = C dxdy 222
234 siedo C x 2 + y 2. Si se cosidera como u recito de tipo I, debemos hallar las ecuacioes de las dos curvas que delimita el recito por su parte iferior y superior, tal y como se ve e la Fig. 0.3 Figura 0.3: Disco uidad por lo que los límites de itegració será x C x 2 y x 2 Por tato, dxdy = C ( x 2 x 2 dy ) dx = 2 x 2 dx x = si t dx = cos t dt y, haciedo el cambio de variable x = t = π 2 x = t = π 2, resulta = π 2 π 2 2 cos 2 t dt = [ t + si(2t) ] t= π 2 2 t= π = π
235 Más adelate se verá que este tipo de itegrales puede resolverse de forma más secilla, aplicado el cambio de variables a la itegral doble. Ejercicio 0.8 Cosidera u triágulo isósceles co u vértice e el puto (0, 0) y los lados iguales sobre las rectas determiadas por y = x. Halla qué altura, h, debe teer el triágulo sobre el eje OY para que la circuferecia uidad lo divida e dos partes de igual área. (Sol.: h = 2π 2 ) 0.2. Itegrales triples Las itegrales triples o tiee ya mayor dificultad salvo la añadida por ua dimesió más. Los rectágulos ateriores se substituye ahora por rectágulos tridimesioales, o sea, cajas R = [a, b] [c, d] [p, q]. Ua partició P de R es ahora P = P P 2 P 3 siedo P, P 2 y P 3 particioes de los itervalos [a, b], [c, d] y [p, q], co respectivamete. Si P tiee + putos, P tiee m + putos y P 3 tiee r + putos, la partició P = P P 2 P 3 divide al rectágulo R e m r subrectágulos R ijk = [x i, x i ] [y j, y j ] [z k, z k ]; cada uo de los cuales tiee volume v(r ijk = (x i x i )(y j y j )(z k z k ) Procediedo de forma similar al caso de dos variables, dada ua fució real acotada f defiida e R, se defie la suma de Riema correspodiete a la partició de P de R como S(f, P ) = m r f(x ijk )v(r ijk ) i= j= k= co x ijk R ijk. Defiició 0.9 Dada la fució acotada f : R R se defie la itegral triple como el límite de las sumas de Riema cuado P tiede a 0: R f(x, y, z)dxdydz = 224 lím P 0 j= f(x jkl )v(r jkl )
236 siempre que dicho límite exista y sea idepediete de la elecció del puto x ijk. Como ates, toda fució cotiua es itegrable y toda fució acotada cuyas discotiuidades tiee medida ula es itegrable. Asimismo se cumple las propiedades del Teorema 0.2. Fialmete, el cálculo de ua itegral triple puede reducirse al cálculo de tres itegrales iteradas: Teorema 0.0 Sea f ua fució itegrable sobre u rectágulo R = [a, b] [c, d] [p, q]. Si existe cualquier itegral iterada, es igual a la itegral triple R f(x, y, z)dxdydz = = = b a d c q p =... ( d ( q c p ( q ( b p a ( b ( d a c ) f(x, y, z)dz ) f(x, y, z)dx ) f(x, y, z)dy ) dy dx ) dz dy ) dx dz y así sucesivamete hasta completar todas las ordeacioes posibles. Ejemplo 0.8 Calcular la itegral sobre R = [, ] [0, 2] [, 2] de la fució f(x, y, z) = xyz Solució: Se tiee que xyz dxdydz = R = = ( 2 ( 2 0 ) xyz dz ( 2 [ ] z 2 z=2 xy dy 0 2 z= [ ] 3 y 2 y=2 2 x dx = 2 y=0 ) dy ) dx dx = 3x dx = 0 ( 2 0 ) 3 xy dy 2 dx 225
237 Ejercicio 0.9 Averigua cómo platear la itegral aterior para obteer el resultado más rápidamete Itegració sobre recitos acotados Al igual que sucedía e el caso de itegrales dobles, la itegral triple sobre recitos acotados se hace extediedo la itegral a u rectágulo y utilizado la fució característica: f(x, y, z) dxdydz := f(x, y, z) χ Ω (x, y, z) dxdydz Ω siedo R u rectágulo que cotiee a Ω. Para el cálculo de la itegral, el procedimieto ahora cosiste e expresar el recito e algua de las formas siguietes: Ω = {(x, y, z) : (x, y) D, ϕ (x, y) z ϕ 2 (x, y)} siedo D = proy XOY (Ω) y ϕ, ϕ 2 fucioes cotiuas. Ω = {(x, y, z) : (x, z) D, ϕ (x, z) y ϕ 2 (x, z)} siedo D = proy XOZ (Ω) y ϕ, ϕ 2 fucioes cotiuas. Ω = {(x, y, z) : (y, z) D, ϕ (y, z) x ϕ 2 (y, z)} siedo D = proy Y OZ (Ω) y ϕ, ϕ 2 fucioes cotiuas. A cotiuació el recito D R 2 se expresa como de tipo I o de tipo II, dado lugar a la itegral iterada correspodiete. Por ejemplo, e el primer caso, si D es de tipo II e el plao XOY, se tedrá: α y β Ω g (y) x g 2 (y) ϕ (x, y) z ϕ 2 (x, y) y, por tato, Ω f(x, y, z) dxdydz = β α R ( ( g2 (y) ) ) ϕ 2 (x, y)f(x, y, z) dz dx dy g (y) ϕ (x,y) 226
238 Ejemplo 0.9 Se desea calcular el volume del tetraedro limitado por los plaos coordeados y el plao x+y +z =. Para ello será ecesario calcular Ω dxdydz, siedo Ω el tetraedro. Para calcular los límites de itegració se proyecta el recito sobre el plao XOY obteiedo el triágulo señalado e la figura Fig Las variables (x, y) varía e dicho triágulo, mietras que z recorre el recito desde la superficie iferior z = 0 hasta la superficie superior z = x y. Figura 0.4: Volume de u tetraedro Por todo ello resulta: 0 x Ω 0 y x 0 z x y 227
239 y, etoces Ω dxdydz = = = = = ( x ( x y 0 0 ( x [x x 2 + x3 3 0 ) dz ) ( x y) dy dx ] y= x ) dy dx [y xy y2 dx 2 y=0 ) ( x)2 ( x x( x) dx 2 ] x= ( x)3 + = 6 x=0 3 6 = 6 Ejercicio 0.0 Calcular el volume del cuerpo limitado por z 2 = xy, x + y =, x + y = 2. (Sol.: 7π 2 u3 ) 0.3. Cambio de variable Ua trasformació e el plao es ua aplicació T : R 2 R 2 co T (u, v) = (x, y). Se llama determiate jacobiao de T a x x (x, y) (u, v) = u v Teorema 0. (Dos variables) Sea D y D dos regioes elemetales del plao y sea T : D D ua biyecció de clase C, cuyo determiate jacobiao o se aula e D. Etoces, para cualquier fució itegrable f : D R se tiee f(x, y) dxdy = (f T )(u, v) (x, y) D D (u, v) dudv y u y v 228
240 Cambio a coordeadas polares Es el dado por la trasformació T : D = [0, ] [0, 2π[ R 2 dode (x, y) = T (r, θ) = (r cos θ, r si θ) Puede probarse fácilmete que T cumple las codicioes del teorema de cambio de variable y, además, su jacobiao es x x (x, y) (r, θ) = r θ = cos θ r si θ si θ r cos θ = r y r y θ Supogamos que queremos calcular ua itegral doble R f(x, y) da cuado R es u domiio como e la figura Fig La descripció de u domiio de este tipo e coordeadas rectagulares parece bastate complicada, si embargo describir R e coordeadas polares os simplificará bastate las cosas Figura 0.5: U aillo circular E geeral, las coordeadas polares so adecuadas cuado el recito de itegració es u círculo de cetro el orige (o u sector circular) o, al meos, u círculo tagete al orige. E los siguietes ejemplos vamos a aplicar dicho cambio y hay que teer mucho cuidado de o olvidar multiplicar por r al hacer el cambio a coordeadas polares e la itegral. Ejemplo 0.0 Calculemos la itegral doble R (3x+4y2 ) da dode R es la regió circular que se ecuetra e el semiplao superior y está limitada por las circuferecias x 2 + y 2 = y x 2 + y 2 = 4, como puede verse e la siguiete figura: 229
241 2 2 x + y = x + y = -2-2 Figura 0.6: Itegració e coordeadas polares Solució: La regió R se describe como: Por tato: R R = {(r, θ)/ r 2 ; 0 θ π} (3x + 4y 2 ) da = = = = π 2 0 π 0 π 0 π 0 (3r cos(θ) + 4(r se(θ)) 2 ) r drdθ [ r 3 cos(θ) + r 4 se 2 (θ) ] r=2 r= dθ 7 cos(θ) + 5 se 2 (θ) dθ 7 cos(θ) ( cos(2θ)) dθ = 7 se(θ) + 5θ se(2θ) ] π 0 = 5π 2 Ejemplo 0. Veamos como calcular el volume del sólido que está limitado por los plaos z = 3, z = 0 y el cilidro x2 + y 2 = y. Solució: Este sólido está ecima del disco que tiee como círculo frotera a la circuferecia x 2 +y 2 = y = x 2 +y 2 y = 0 = x 2 +y 2 y ( 4 4 = 0 = x2 + y ) 2 =
242 es decir, tiee como frotera la circuferecia de cetro el puto (0, /2) y radio 2 (ver figura Fig. 0.7). Si cosideramos coordeadas polares, se tiee que este circulo se expresa como: x 2 +y 2 = y = r 2 cos 2 (θ)+r 2 se 2 (θ) = r se(θ) = r 2 = r se(θ) = r = se(θ) Por lo tato, el disco sobre el que se ecuetra el sólido está dado por: D = {(r, θ)/0 r se(θ) ; 0 θ π} r = se(θ) (a) Sólido (b) Proyecció e el plao XOY Figura 0.7: Volume de u cilidro circular Aplicado la fórmula de itegració e coordeadas polares: Vol = D π 3 da = = 0 π 0 se(θ) 0 π 3 rdrdθ = 0 r 2 ] se(θ) 6 cos(2θ) dθ = θ 2 2 se(2θ) 24 0 dθ = ] π 0 π 0 = π 2 se 2 (θ) dθ 6 Ejemplo 0.2 Calcular el área ecerrada por las hojas de ua rosa de cuatro pétalos, co ecuació es r = cos(2θ). 23
243 Solució: Recordar que área(d) = D dxdy. Como se observa e la gráfica, Fig. 0.8, para calcular el área ecerrada por las hojas de ua rosa de cuatro pétalos, os bastará co calcular el área ecerrada e la mitad de u sólo pétalo; es decir, el cojuto sobre el que vamos a itegrar es D = {(r, θ)/0 r cos(2θ) ; 0 θ π 4 } π/ π/4 Figura 0.8: Ua rosa de cuatro pétalos Luego, el área que buscamos es: Área = P π 4 da = 8 0 π 4 = 4 cos 2 (2θ) = 4 0 cos(2θ) 0 π 4 0 π 4 r dr dθ = 8 0 ( ) cos(4θ) + 2 r 2 ] cos(2θ) dθ 2 0 = 4 ( θ 2 + se(4θ) )] π dθ = π 2 Ejemplo 0.3 Calcula la itegral S = {(x, y) R 2 / x 2 + y 2 } S xy dxdy dode S es el recito Solució: La ecuació x 2 + y 2 = represeta ua circuferecia cetrada e (0, 0) de radio. Así, la iequació x 2 + y 2 < correspode a los putos 232
244 iteriores a la circuferecia y, por tato, el recito S es el disco uidad represetado e la Figura 0.9. Esta itegral se resolverá utilizado el cambio a coordeadas polares. Así, el recito S se trasforma e D = {(r, θ) : 0 r ; 0 θ 2π} Figura 0.9: Disco uidad xy dxdy = (r cos θ)(r si θ)r drdθ = S D 2π ( ) = r 3 cos θ si θ dr dθ = = 0 2π 0 2π 0 [ r 4 cos θ si θ 4 = cos θ si θ = 4 0 = [ si 2 ] θ=2π θ = θ=0 ] r= r=0 dθ =
IES IGNACIO ALDECOA 1 AMPLIACIÓN DE MATEMÁTICAS 4º ESO CURSO 10/11
 IES IGNACIO ALDECOA AMPLIACIÓN DE MATEMÁTICAS º ESO CURSO 0/ TEMA : SUCESIONES DE NÚMEROS REALES Se llama sucesió a u cojuto de úmeros dispuestos uo a cotiuació de otro. Podemos cosiderar ua sucesió como
IES IGNACIO ALDECOA AMPLIACIÓN DE MATEMÁTICAS º ESO CURSO 0/ TEMA : SUCESIONES DE NÚMEROS REALES Se llama sucesió a u cojuto de úmeros dispuestos uo a cotiuació de otro. Podemos cosiderar ua sucesió como
6. Sucesiones y Series numéricas Sucesiones numéricas DEFINICIONES
 6. Sucesioes y Series uméricas 6.. Sucesioes uméricas 6... DEFINICIONES Sucesioes de úmeros reales Se llama sucesió de úmeros reales a cualquier lista ordeada de úmeros reales: a, a 2, a 3,..., a,...,
6. Sucesioes y Series uméricas 6.. Sucesioes uméricas 6... DEFINICIONES Sucesioes de úmeros reales Se llama sucesió de úmeros reales a cualquier lista ordeada de úmeros reales: a, a 2, a 3,..., a,...,
AMPLIACIÓN DE MATEMÁTICAS 4º ESO CURSO 1 /1
 AMPLIACIÓN DE MATEMÁTICAS º ESO CURSO / TEMA : SUCESIONES DE NÚMEROS REALES Se llama sucesió a u cojuto de úmeros dispuestos uo a cotiuació de otro. Podemos cosiderar ua sucesió como ua fució que asiga
AMPLIACIÓN DE MATEMÁTICAS º ESO CURSO / TEMA : SUCESIONES DE NÚMEROS REALES Se llama sucesió a u cojuto de úmeros dispuestos uo a cotiuació de otro. Podemos cosiderar ua sucesió como ua fució que asiga
SERIES NUMÉRICAS. SECCIONES A. Series de términos no negativos. B. Ejercicios propuestos.
 CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
Los números complejos
 Los úmeros complejos Los úmeros complejos Forma biómica Defiició z = a + bi, o bie, z = (a, b) siedo a la parte real y b la parte imagiaria. a = r cos α b = r se α Opuesto z = a bi Cojugado z = a bi Represetació
Los úmeros complejos Los úmeros complejos Forma biómica Defiició z = a + bi, o bie, z = (a, b) siedo a la parte real y b la parte imagiaria. a = r cos α b = r se α Opuesto z = a bi Cojugado z = a bi Represetació
Sucesiones de números reales
 Sucesioes de úmeros reales Defiició y propiedades Sucesioes de úmeros reales 4 4 Defiició y propiedades 47 4 Sucesioes parciales 49 43 Mootoía 50 44 Sucesioes divergetes 53 45 Criterios de covergecia 54
Sucesioes de úmeros reales Defiició y propiedades Sucesioes de úmeros reales 4 4 Defiició y propiedades 47 4 Sucesioes parciales 49 43 Mootoía 50 44 Sucesioes divergetes 53 45 Criterios de covergecia 54
6. Sucesiones y Series numéricas Series numéricas DEFINICIONES Y PROPIEDADES
 6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
Ejemplo: 0+0i y -3+0i representan los números reales 0 y 3 respectivamente. Si a=0 se considera un número imaginario puro a 0+bi
 u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
Negativos: 3, 2, 1 = 22. ab/c 11 Æ 18
 Los úmeros reales.. Los úmeros reales El cojuto de los úmeros reales está formado por los úmeros racioales y los irracioales. Se represeta por la letra Los úmeros racioales so los úmeros eteros, los decimales
Los úmeros reales.. Los úmeros reales El cojuto de los úmeros reales está formado por los úmeros racioales y los irracioales. Se represeta por la letra Los úmeros racioales so los úmeros eteros, los decimales
( ) = 1= + + ( ) + + lim 3x 5 = lim 3x lim5 = lim3 lim x lim5 = = 12 5 = 7
 LÍMITES DE FUNCIONES POLINÓMICAS Límites de ua fució costate f k, k El límite de ua fució costate es la misma costate f k f k k k a a Límites de la fució idetidad I I a a a I I Límites e u puto fiito.
LÍMITES DE FUNCIONES POLINÓMICAS Límites de ua fució costate f k, k El límite de ua fució costate es la misma costate f k f k k k a a Límites de la fució idetidad I I a a a I I Límites e u puto fiito.
Tema 1: Números Complejos
 Números Complejos Tema 1: Números Complejos Deició U úmero complejo es u par ordeado (x, y) de úmeros reales Éste puede iterpretarse como u puto del plao cuya abscisa es x y cuya ordeada es y El cojuto
Números Complejos Tema 1: Números Complejos Deició U úmero complejo es u par ordeado (x, y) de úmeros reales Éste puede iterpretarse como u puto del plao cuya abscisa es x y cuya ordeada es y El cojuto
El tema de este capítulo es el estudio de las sucesiones de números reales. Una sucesión no es más que un conjunto ordenado de números.
 Capítulo 3 Sucesioes 3 Defiicioes Geerales El tema de este capítulo es el estudio de las sucesioes de úmeros reales Ua sucesió o es más que u cojuto ordeado de úmeros Por ejemplo, 2, 4, 6, 8, 0, 2,, 2,
Capítulo 3 Sucesioes 3 Defiicioes Geerales El tema de este capítulo es el estudio de las sucesioes de úmeros reales Ua sucesió o es más que u cojuto ordeado de úmeros Por ejemplo, 2, 4, 6, 8, 0, 2,, 2,
Tema 8 Límite de Funciones. Continuidad
 Tema 8 Límite de Fucioes. Cotiuidad 1. Operacioes co límites. Los límites de las sucesioes a b, c, d y e so los idicados e la tabla siguiete:, a b c d e - 0 1 Di cual es el límite de: a) lim( a b ) c)
Tema 8 Límite de Fucioes. Cotiuidad 1. Operacioes co límites. Los límites de las sucesioes a b, c, d y e so los idicados e la tabla siguiete:, a b c d e - 0 1 Di cual es el límite de: a) lim( a b ) c)
Tema 1 Los números reales Matemáticas I 1º Bachillerato 1
 Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Tema 4 Sucesiones numéricas
 Tema 4 Sucesioes uméricas Objetivos 1. Defiir sucesioes co wxmaxima. 2. Calcular elemetos de ua sucesió. 3. Realizar operacioes co sucesioes. 4. Iterpretar la defiició de límite de ua sucesió. 5. Calcular
Tema 4 Sucesioes uméricas Objetivos 1. Defiir sucesioes co wxmaxima. 2. Calcular elemetos de ua sucesió. 3. Realizar operacioes co sucesioes. 4. Iterpretar la defiició de límite de ua sucesió. 5. Calcular
Problemas de Sucesiones
 Capítulo Problemas de Sucesioes Problema. Calcular los siguietes ites: l se i e + 3 ii 5 iii l iv + + + Solució: l se i [ escala de iitos se acotada ] 0 acotada 0. e + e ii 5 + [ úmero meor que uo 5 ]
Capítulo Problemas de Sucesioes Problema. Calcular los siguietes ites: l se i e + 3 ii 5 iii l iv + + + Solució: l se i [ escala de iitos se acotada ] 0 acotada 0. e + e ii 5 + [ úmero meor que uo 5 ]
INTEGRALES DE RIEMANN
 NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES DE RIEMANN Ig. Jua Sacerdoti Departameto de Matemática Facultad de Igeiería Uiversidad de Bueos Aires 00 INDICE.- INTEGRAL..- INTRODUCCIÓN..-
NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES DE RIEMANN Ig. Jua Sacerdoti Departameto de Matemática Facultad de Igeiería Uiversidad de Bueos Aires 00 INDICE.- INTEGRAL..- INTRODUCCIÓN..-
Tema 5 Series numéricas
 Tema 5 Series uméricas Objetivos 1. Defiir series co wxmaxima. 2. Calcular sumas parciales de ua serie. 3. Iterpretar la defiició de suma de ua serie. 4. Calcular la suma de ua serie geométrica. 5. Calcular
Tema 5 Series uméricas Objetivos 1. Defiir series co wxmaxima. 2. Calcular sumas parciales de ua serie. 3. Iterpretar la defiició de suma de ua serie. 4. Calcular la suma de ua serie geométrica. 5. Calcular
Límite y Continuidad de Funciones.
 Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Series Numéricas. Una forma de definir e es a través de la suma: 1. 1 0! + 1 1! + 1 2! + 1 3! + 1 4! + + 1 n. cuyo límite es e, es decir:
 Capítulo Series Numéricas Las series uméricas so sucesioes muy particulares ya que se defie (o se geera) a partir de otra sucesió. Dos ejemplos secillos aparece e la defiició de e y el la Paradoja de Zeó.
Capítulo Series Numéricas Las series uméricas so sucesioes muy particulares ya que se defie (o se geera) a partir de otra sucesió. Dos ejemplos secillos aparece e la defiició de e y el la Paradoja de Zeó.
3. Volumen de un sólido.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Itegrales y aplicacioes.. Volume de u sólido. E esta secció veremos cómo podemos utilizar la itegral defiida para calcular volúmees de distitos tipos
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Itegrales y aplicacioes.. Volume de u sólido. E esta secció veremos cómo podemos utilizar la itegral defiida para calcular volúmees de distitos tipos
SUCESIONES Y SERIES DE FUNCIONES
 CAPÍTULO XV. SUCESIONES Y SERIES DE FUNCIONES SECCIONES A. Campo de covergecia. Covergecia uiforme. B. Series de potecias. Itervalos de covergecia. C. Desarrollo de fucioes e series de potecias. D. Aplicacioes
CAPÍTULO XV. SUCESIONES Y SERIES DE FUNCIONES SECCIONES A. Campo de covergecia. Covergecia uiforme. B. Series de potecias. Itervalos de covergecia. C. Desarrollo de fucioes e series de potecias. D. Aplicacioes
SUCESIONES DE NÚMEROS REALES. PROGRESIONES
 www.matesxroda.et José A. Jiméez Nieto SUCESIONES DE NÚMEROS REALES. PROGRESIONES. SUCESIONES DE NÚMEROS REALES. TÉRMINO GENERAL E las siguietes figuras observa el proceso que lleva a la creació de uevos
www.matesxroda.et José A. Jiméez Nieto SUCESIONES DE NÚMEROS REALES. PROGRESIONES. SUCESIONES DE NÚMEROS REALES. TÉRMINO GENERAL E las siguietes figuras observa el proceso que lleva a la creació de uevos
FUNCIONES. ( a) IGUALDAD DE FUNCIONES Sí y son dos funciones, diremos que las funciones f y
 CALCULO P.C.I. PRIMER SEMESTRE 04 FUNCIONES Sí A y B so dos cojutos o vacío, ua fució de A e B asiga a cada elemeto a perteeciete al cojuto A u úico elemeto b de B que deomiamos image de a. Además diremos
CALCULO P.C.I. PRIMER SEMESTRE 04 FUNCIONES Sí A y B so dos cojutos o vacío, ua fució de A e B asiga a cada elemeto a perteeciete al cojuto A u úico elemeto b de B que deomiamos image de a. Además diremos
LOS NUMEROS REALES. Conjunto no vacío designado como R y denominado conjunto de los números reales. En
 LOS NUMEROS REALES Cojuto o vacío desigado como R y deomiado cojuto de los úmeros reales. E él se defie ua relació de igualdad = y dos operacioes algebraicas + y. Relació de igualdad Defiició: R = (a,b)
LOS NUMEROS REALES Cojuto o vacío desigado como R y deomiado cojuto de los úmeros reales. E él se defie ua relació de igualdad = y dos operacioes algebraicas + y. Relació de igualdad Defiició: R = (a,b)
Series de potencias. Desarrollos en serie de Taylor
 Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
con operacion inversa la resta (suma de opuestos) y una operacion producto escalar, que no es interna,
 Tema 9 El plao complejo 9. Números complejos E IR, las operacioes suma producto de úmeros reales so operacioes iteras (el resultado de operar es otro úmero real) que permite la existecia de operacioes
Tema 9 El plao complejo 9. Números complejos E IR, las operacioes suma producto de úmeros reales so operacioes iteras (el resultado de operar es otro úmero real) que permite la existecia de operacioes
Cálculo de límites Criterio de Stolz. Tema 8
 Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
CAPÍTULO VIII. CONVERGENCIA DE SUCESIONES. SECCIONES A. Criterios de convergencia. B. Ejercicios propuestos.
 CAPÍTULO VIII CONVERGENCIA DE SUCESIONES SECCIONES A Criterios de covergecia B Ejercicios propuestos 347 A CRITERIOS DE CONVERGENCIA Ua fució cuyo domiio es el cojuto de los úmeros aturales se dice sucesió
CAPÍTULO VIII CONVERGENCIA DE SUCESIONES SECCIONES A Criterios de covergecia B Ejercicios propuestos 347 A CRITERIOS DE CONVERGENCIA Ua fució cuyo domiio es el cojuto de los úmeros aturales se dice sucesió
Los números complejos ( )
 Los úmeros complejos (15.06.016) 1. Itroducció Estas otas se propoe u doble objetivo. Co los apartados a 8 se pretede dar uas ocioes básicas sobre los úmeros complejos que ayude a fijar los coceptos expuestos
Los úmeros complejos (15.06.016) 1. Itroducció Estas otas se propoe u doble objetivo. Co los apartados a 8 se pretede dar uas ocioes básicas sobre los úmeros complejos que ayude a fijar los coceptos expuestos
LAS SERIES GEOMÉTRICAS Y SU TENDENCIA AL INFINITO
 LA ERIE GEOMÉTRICA Y U TENDENCIA AL INFINITO ugerecias al Profesor: Al igual que las sucesioes, las series geométricas se itroduce como objetos matemáticos que permite modelar y resolver problemas que
LA ERIE GEOMÉTRICA Y U TENDENCIA AL INFINITO ugerecias al Profesor: Al igual que las sucesioes, las series geométricas se itroduce como objetos matemáticos que permite modelar y resolver problemas que
UNEFA C.I.N.U. Matemáticas
 RADICACIÓN: DEFINICIÓN Y PROPIEDADES Ates de etrar e el tema Radicació, vamos a comezar por recordar u poco sore Poteciació: Saemos que e lugar de escriir, utilizamos la otació: de Poteciació, dode el
RADICACIÓN: DEFINICIÓN Y PROPIEDADES Ates de etrar e el tema Radicació, vamos a comezar por recordar u poco sore Poteciació: Saemos que e lugar de escriir, utilizamos la otació: de Poteciació, dode el
Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de una variable. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación
 Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
Medidas de Tendencia Central
 1 Medidas de Tedecia Cetral La Media La media (o promedio) de ua muestra x 1, x,, x de tamaño de ua variable o característica x, se defie como la suma de todos los valores observados e la muestra, dividida
1 Medidas de Tedecia Cetral La Media La media (o promedio) de ua muestra x 1, x,, x de tamaño de ua variable o característica x, se defie como la suma de todos los valores observados e la muestra, dividida
Sistemas de Ecuaciones Lineales. M. en I. Gerardo Avilés Rosas
 Sistemas de Ecuacioes Lieales M. e I. Gerardo Avilés Rosas Octubre de 206 Tema 5 Sistemas de Ecuacioes Lieales Objetivo: El alumo formulará, como modelo matemático de problemas, sistemas de ecuacioes lieales
Sistemas de Ecuacioes Lieales M. e I. Gerardo Avilés Rosas Octubre de 206 Tema 5 Sistemas de Ecuacioes Lieales Objetivo: El alumo formulará, como modelo matemático de problemas, sistemas de ecuacioes lieales
Sucesiones Numéricas. Tema 2
 Tema 2 Sucesioes Numéricas Imagiemos la cola de etrada a u espectáculo formada por persoas que ha sido umeradas de la forma habitual; el primero de la cola lleva el úmero 1, el segudo el úmero 2 y así
Tema 2 Sucesioes Numéricas Imagiemos la cola de etrada a u espectáculo formada por persoas que ha sido umeradas de la forma habitual; el primero de la cola lleva el úmero 1, el segudo el úmero 2 y así
Números naturales, enteros y racionales
 Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
Funciones de variable compleja
 Tema 10 Fucioes de variable compleja 10.1 Fucioes complejas de variable compleja Defiició 10.1 Ua fució compleja de variable compleja es ua aplicació f: A C dode A C. Para cada z A, fz) C, luego fz) =
Tema 10 Fucioes de variable compleja 10.1 Fucioes complejas de variable compleja Defiició 10.1 Ua fució compleja de variable compleja es ua aplicació f: A C dode A C. Para cada z A, fz) C, luego fz) =
Una serie de potencias puede ser interpretada como una función de x. f(x) = n=0
 Tema 4 Series de Potecias Ua expresió de la forma a 0 + a 1 (x c) + a 2 (x c) 2 +... + a (x c) +... = recibe el ombre de serie de potecias cetrada e c. a (x c) Ua serie de potecias puede ser iterpretada
Tema 4 Series de Potecias Ua expresió de la forma a 0 + a 1 (x c) + a 2 (x c) 2 +... + a (x c) +... = recibe el ombre de serie de potecias cetrada e c. a (x c) Ua serie de potecias puede ser iterpretada
Sucesiones. Se denomina sucesión a una función cuyo dominio es el conjunto de los números naturales.
 Sucesioes Sucesió Se deomia sucesió a ua fució cuyo domiio es el cojuto de los úmeros aturales. Para deotar el -ésimo elemeto de la sucesió se escribe a e lugar de f(). Ejemplo: a = 1/ a 1 = 1, a 2 = 1/2,
Sucesioes Sucesió Se deomia sucesió a ua fució cuyo domiio es el cojuto de los úmeros aturales. Para deotar el -ésimo elemeto de la sucesió se escribe a e lugar de f(). Ejemplo: a = 1/ a 1 = 1, a 2 = 1/2,
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 3º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
Elementos de Análisis Matemático
 Elemetos de Aálisis Matemático Curso 005-006, grupo A, Pedro López Rodríguez Pla de la asigatura TEMARIO Tema. El úmero real. Los úmeros aturales, eteros, racioales y reales. Pricipio de iducció. Itroducció
Elemetos de Aálisis Matemático Curso 005-006, grupo A, Pedro López Rodríguez Pla de la asigatura TEMARIO Tema. El úmero real. Los úmeros aturales, eteros, racioales y reales. Pricipio de iducció. Itroducció
PRÁCTICAS DE ANÁLISIS DE UNA VARIABLE
 PRÁCTICAS DE ANÁLISIS DE UNA VARIABLE Departameto de Aálisis Matemático Curso 00/003 Profesores resposables Oscar Blasco Atoio Galbis Jesús García Josep Martíez Aíbal Moltó Carme de las Obras Sergio Segura
PRÁCTICAS DE ANÁLISIS DE UNA VARIABLE Departameto de Aálisis Matemático Curso 00/003 Profesores resposables Oscar Blasco Atoio Galbis Jesús García Josep Martíez Aíbal Moltó Carme de las Obras Sergio Segura
Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 5. Series.
 CÁLCULO Igeiería Idustrial. Curso 2009-200. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Lecció 5. Series. Resume de la lecció. 5.. Sucesioes y series. Sucesió covergete. Se de e ua sucesió
CÁLCULO Igeiería Idustrial. Curso 2009-200. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Lecció 5. Series. Resume de la lecció. 5.. Sucesioes y series. Sucesió covergete. Se de e ua sucesió
R. Urbán Ruiz (notas de clase)
 R. Urbá Ruiz (otas de clase) Fucioes E las ciecias Ecoómicas las fucioes so de mucho valor para resolver problemas dode haya que relacioar variables; como por ejemplo, la producció, la oferta, la demada,
R. Urbá Ruiz (otas de clase) Fucioes E las ciecias Ecoómicas las fucioes so de mucho valor para resolver problemas dode haya que relacioar variables; como por ejemplo, la producció, la oferta, la demada,
Importancia de las medidas de tendencia central.
 UNIDAD 5: UTILICEMOS MEDIDAS DE TENDENCIA CENTRAL. Importacia de las medidas de tedecia cetral. Cuado recopilamos ua serie de datos podemos resumirlos utilizado ua tabla de clases y frecuecias. La iformació
UNIDAD 5: UTILICEMOS MEDIDAS DE TENDENCIA CENTRAL. Importacia de las medidas de tedecia cetral. Cuado recopilamos ua serie de datos podemos resumirlos utilizado ua tabla de clases y frecuecias. La iformació
CAPÍTULO V. SUCESIONES Y SERIES
 (Aputes e revisió para orietar el apredizaje) CAPÍTULO V. UCEIONE Y ERIE DEFINICIÓN. Ua sucesió ifiita, o simplemete sucesió, es ua fució cuyo domiio está costituido por el cojuto de los úmeros aturales
(Aputes e revisió para orietar el apredizaje) CAPÍTULO V. UCEIONE Y ERIE DEFINICIÓN. Ua sucesió ifiita, o simplemete sucesió, es ua fució cuyo domiio está costituido por el cojuto de los úmeros aturales
Técnicas para problemas de desigualdades
 Técicas para problemas de desigualdades Notas extraídas del libro de Arthur Egel [] 5 de marzo de 00 Medias Comezamos co dos de las desigualdades más básicas pero al mismo tiempo más importates Sea x,
Técicas para problemas de desigualdades Notas extraídas del libro de Arthur Egel [] 5 de marzo de 00 Medias Comezamos co dos de las desigualdades más básicas pero al mismo tiempo más importates Sea x,
MOSAICOS Y POLIEDROS REGULARES. UN PUNTO DE VISTA FUNCIONAL. Resumen: En este artículo se muestra como las transformaciones de funciones resultan
 MOSAICOS Y POLIEDROS REGULARES. UN PUNTO DE VISTA FUNCIONAL Viceç Fot Departamet de Didàctica de les CCEE i de la Matemàtica de la Uiversitat de Barceloa Resume: E este artículo se muestra como las trasformacioes
MOSAICOS Y POLIEDROS REGULARES. UN PUNTO DE VISTA FUNCIONAL Viceç Fot Departamet de Didàctica de les CCEE i de la Matemàtica de la Uiversitat de Barceloa Resume: E este artículo se muestra como las trasformacioes
TEMA IV. 1. Series Numéricas
 TEMA IV Series uméricas. Ídice. Series uméricas. 2. Propiedades geerales de las series. 3. Series de térmios positivos. Covergecia. 4. Series alteradas. 5. Series de térmios arbitrarios. 6. Ejercicios
TEMA IV Series uméricas. Ídice. Series uméricas. 2. Propiedades geerales de las series. 3. Series de térmios positivos. Covergecia. 4. Series alteradas. 5. Series de térmios arbitrarios. 6. Ejercicios
TEMA 26 DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. DERIVADAS SUCESIVAS. APLICACIONES.
 Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
IES ATENEA. EXAMEN DE RECUPERACIÓN DE MATEMÁTICAS. 3º ESO A. Nombre:
 IES ATENEA. EXAMEN DE RECUPERACIÓN DE MATEMÁTICAS. º ESO A Nombre: Evaluació: Primera. Feca: 0 de diciembre de 00 NOTA Ejercicio º.- Aplica el orde de prioridad de las operacioes para calcular: 64 : 5
IES ATENEA. EXAMEN DE RECUPERACIÓN DE MATEMÁTICAS. º ESO A Nombre: Evaluació: Primera. Feca: 0 de diciembre de 00 NOTA Ejercicio º.- Aplica el orde de prioridad de las operacioes para calcular: 64 : 5
Números naturales, enteros y racionales
 Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
2.- ESPACIOS VECTORIALES. MATRICES.
 2.- ESPACIOS VECTORIALES. MATRICES. 2.1. -ESPACIOS VECTORIALES Sea u cojuto V, etre cuyos elemetos (a los que llamaremos vectores) hay defiidas dos operacioes: SUMA DE DOS ELEMENTOS DE V: Si u, v V, etoces
2.- ESPACIOS VECTORIALES. MATRICES. 2.1. -ESPACIOS VECTORIALES Sea u cojuto V, etre cuyos elemetos (a los que llamaremos vectores) hay defiidas dos operacioes: SUMA DE DOS ELEMENTOS DE V: Si u, v V, etoces
LAS SUCESIONES Y SU TENDENCIA AL INFINITO
 LAS SUCESIONES Y SU TENDENCIA AL INFINITO Sugerecias al Profesor: Resaltar que las sucesioes geométricas ifiitas so objetos matemáticos que permite modelar alguos procesos ifiitos, y que a la vez su costrucció
LAS SUCESIONES Y SU TENDENCIA AL INFINITO Sugerecias al Profesor: Resaltar que las sucesioes geométricas ifiitas so objetos matemáticos que permite modelar alguos procesos ifiitos, y que a la vez su costrucció
INECUACIONES. Ejemplo: La desigualdad 2x+l>x+5, es una inecuación por que tiene una incógnita "x" que se verifica para valores mayores que 4.
 INECUACIONES DEFINICIÓN: Ua iecuació es ua desigualdad e las que hay ua o más catidades descoocidas (icógita) y que sólo se verifica para determiados valores de la icógita o icógitas. Ejemplo: La desigualdad
INECUACIONES DEFINICIÓN: Ua iecuació es ua desigualdad e las que hay ua o más catidades descoocidas (icógita) y que sólo se verifica para determiados valores de la icógita o icógitas. Ejemplo: La desigualdad
Números reales Números. irracionales. Figura 3.1. Construcción del conjunto de los números complejos.
 Números Complejos El cojuto de los úmeros complejos La supremacía de los úmeros reales como cojuto umérico máximo duró poco; o existe u úmero real a que satisfaga la ecuació x 2 + a = 0. Para ello, es
Números Complejos El cojuto de los úmeros complejos La supremacía de los úmeros reales como cojuto umérico máximo duró poco; o existe u úmero real a que satisfaga la ecuació x 2 + a = 0. Para ello, es
TEMA 25 (Oposiciones de Matemáticas)
 TEMA 25 (Oposicioes de Matemáticas) LÍMITES DE FUNCIONES. CONTINUIDAD Y DISCONTINUIDAD. TEOREMA DE BOLZANO.. Itroducció. 2. Límites de fucioes. 2.. Límite de ua fució e u puto. 2.2. Límites laterales.
TEMA 25 (Oposicioes de Matemáticas) LÍMITES DE FUNCIONES. CONTINUIDAD Y DISCONTINUIDAD. TEOREMA DE BOLZANO.. Itroducció. 2. Límites de fucioes. 2.. Límite de ua fució e u puto. 2.2. Límites laterales.
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
ALGEBRA 9. Curso: 3 E.M. Progresiones aritméticas y geométricas. Colegio SSCC Concepción - Depto. de Matemáticas. Nombre: CURSO:
 Colegio SSCC Cocepció - Depto. de Matemáticas Uidad de Apredizaje: Progresioes aritméticas y geométricas Capacidades/Destreza/Habilidad: Racioamieto Matemático/ Aplicació / Calcular, Resolver Valores/
Colegio SSCC Cocepció - Depto. de Matemáticas Uidad de Apredizaje: Progresioes aritméticas y geométricas Capacidades/Destreza/Habilidad: Racioamieto Matemático/ Aplicació / Calcular, Resolver Valores/
FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL 1 FUNCIONES DE VARIAS VARIABLES.
 FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL FUNCIONES DE VARIAS VARIABLES. DEFINICIONES DE FUNCIONES EN VARIAS VARIABLES. Ua fució de variable es u cojuto de pares ordeados de la forma
FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL FUNCIONES DE VARIAS VARIABLES. DEFINICIONES DE FUNCIONES EN VARIAS VARIABLES. Ua fució de variable es u cojuto de pares ordeados de la forma
1 EXPRESIONES ALGEBRAICAS
 EXPRESIONES ALGEBRAICAS E el leguaje matemático, se deomia expresioes algebraicas a toda combiació de letras y/o úmeros viculados etre si por las operacioes de suma, resta, multiplicació y poteciació de
EXPRESIONES ALGEBRAICAS E el leguaje matemático, se deomia expresioes algebraicas a toda combiació de letras y/o úmeros viculados etre si por las operacioes de suma, resta, multiplicació y poteciació de
CAPÍTULO XIII. SUCESIONES
 CAPÍTULO XIII SUCESIONES NUMÉRICAS SECCIONES A Sucesioes covergetes y límites de oscilació Sucesioes moótoas y acotadas B Sucesioes recurretes C Ejercicios propuestos 59 A SUCESIONES CONVERGENTES Y LÍMITES
CAPÍTULO XIII SUCESIONES NUMÉRICAS SECCIONES A Sucesioes covergetes y límites de oscilació Sucesioes moótoas y acotadas B Sucesioes recurretes C Ejercicios propuestos 59 A SUCESIONES CONVERGENTES Y LÍMITES
La sucesión de Lucas
 a sucesió de ucas María Isabel Viggiai Rocha Cosideramos la sucesió umérica { } defiida por: - - si 3 y y 3. Esta sucesió es coocida como la sucesió de ucas y a sus térmios se los llama úmeros de ucas.
a sucesió de ucas María Isabel Viggiai Rocha Cosideramos la sucesió umérica { } defiida por: - - si 3 y y 3. Esta sucesió es coocida como la sucesió de ucas y a sus térmios se los llama úmeros de ucas.
APLICACIONES INFORMÁTICAS EN QUÍMICA. Problemas Tema 2.3: Series, representación de funciones y construcción de tablas en HC.
 APLICACIONES INFORMÁTICAS EN QUÍMICA Problemas Tema 2.3: Series, represetació de fucioes y costrucció de tablas e HC Grado e Química º SEMESTRE Uiversitat de Valècia Facultad de Químicas Departameto de
APLICACIONES INFORMÁTICAS EN QUÍMICA Problemas Tema 2.3: Series, represetació de fucioes y costrucció de tablas e HC Grado e Química º SEMESTRE Uiversitat de Valècia Facultad de Químicas Departameto de
CLAVES DE CORRECCIÓN GUÍA DE EJERCITACIÓN FACTORES Y PRODUCTOS PREGUNTA ALTERNATIVA Nivel
 x Estimado alumo: Aquí ecotrarás las claves de correcció, las habilidades y los procedimietos de resolució asociados a cada preguta, o obstate, para reforzar tu apredizaje es fudametal que asistas a la
x Estimado alumo: Aquí ecotrarás las claves de correcció, las habilidades y los procedimietos de resolució asociados a cada preguta, o obstate, para reforzar tu apredizaje es fudametal que asistas a la
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Sucesiones y series de números reales 1. Sucesiones de números reales
 - Ferado Sáchez - - 7 Sucesioes Cálculo I y series de úmeros reales Sucesioes de úmeros reales 20 205 De maera similar a como se hizo para sucesioes de úmeros racioales, se defie ua sucesió de úmeros reales
- Ferado Sáchez - - 7 Sucesioes Cálculo I y series de úmeros reales Sucesioes de úmeros reales 20 205 De maera similar a como se hizo para sucesioes de úmeros racioales, se defie ua sucesió de úmeros reales
MATE1214 -Calculo Integral Parcial -3
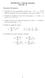 MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
Cálculo de límites. 3.1. Sumas, productos y cocientes. Tema 3
 Tema 3 Cálculo de ites El presete tema tiee u iterés emietemete práctico, pues su pricipal fialidad es aportar los ejemplos que se echaba de meos e el tema aterior. Empezaremos estableciedo las reglas
Tema 3 Cálculo de ites El presete tema tiee u iterés emietemete práctico, pues su pricipal fialidad es aportar los ejemplos que se echaba de meos e el tema aterior. Empezaremos estableciedo las reglas
INTERÉS SIMPLE COMO FUNCIÓN LINEAL.
 INTERÉS SIMPLE COMO FUNCIÓN LINEAL. EJERCICIOS PROPUESTOS. 1.- Grafica las fucioes Moto e Iterés: a) C = + 0, co C e miles de pesos ; : meses y R. Para graficar estar fucioes, debemos dar valores a, por
INTERÉS SIMPLE COMO FUNCIÓN LINEAL. EJERCICIOS PROPUESTOS. 1.- Grafica las fucioes Moto e Iterés: a) C = + 0, co C e miles de pesos ; : meses y R. Para graficar estar fucioes, debemos dar valores a, por
MATEMÁTICAS PARA LOS GRADOS EN ECONOMÍA Y EMPRESA. Cálculo Diferencial Ejercicios y Problemas resueltos
 MATEMÁTICAS PARA LOS GRADOS EN ECONOMÍA Y EMPRESA Cálculo Diferecial Ejercicios y Problemas resueltos Juliá Rodríguez Ruiz (Catedrático de Ecoomía Aplicada. UNED) Mariao Matilla García (Profesor Titular
MATEMÁTICAS PARA LOS GRADOS EN ECONOMÍA Y EMPRESA Cálculo Diferecial Ejercicios y Problemas resueltos Juliá Rodríguez Ruiz (Catedrático de Ecoomía Aplicada. UNED) Mariao Matilla García (Profesor Titular
INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS
 Capítulo INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS Problema Calcula las partes real e imagiaria de los siguietes úmeros complejos: a) i + + i, b) + i i + i + i + i, c) d) + i), + ), + i e) f) ) + i 04, i +
Capítulo INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS Problema Calcula las partes real e imagiaria de los siguietes úmeros complejos: a) i + + i, b) + i i + i + i + i, c) d) + i), + ), + i e) f) ) + i 04, i +
MEDIDAS DE TENDENCIA CENTRAL. _ xi
 EDIDAS DE TENDENCIA CENTRAL. EDIA ARITÉTICA. Es la medida más coocida y tambié es llamada promedio se obtiee sumado todos los valores de la muestra o població, dividida etre el total de elemetos que cotiee
EDIDAS DE TENDENCIA CENTRAL. EDIA ARITÉTICA. Es la medida más coocida y tambié es llamada promedio se obtiee sumado todos los valores de la muestra o població, dividida etre el total de elemetos que cotiee
a 1, a 2, a 3, a 4,..., a n,... La sucesión {a 1, a 2, a 3,...}también se denota mediante a n n 1 a n 1 n n 1 a n sn 3, n 3 a n cos n 3, 4 125, 6
 . SUCESIONES Se puede cosiderar que ua sucesió es ua lista de úmeros escritos e u orde defiido: a, a 2, a 3, a 4,..., a,... El úmero a recibe el ombre de primer térmio, a 2 es el segudo térmio y, e geeral,
. SUCESIONES Se puede cosiderar que ua sucesió es ua lista de úmeros escritos e u orde defiido: a, a 2, a 3, a 4,..., a,... El úmero a recibe el ombre de primer térmio, a 2 es el segudo térmio y, e geeral,
Unidad I: Números Complejos
 Uidad I: Números Complejos INTRODUCCIÓN Desde Al'Khwarimi (800 DC), quie fuera precursor del Álgebra, sólo se obteía las solucioes de las raíces cuadradas de úmeros positivos El matemático italiao Girolamo
Uidad I: Números Complejos INTRODUCCIÓN Desde Al'Khwarimi (800 DC), quie fuera precursor del Álgebra, sólo se obteía las solucioes de las raíces cuadradas de úmeros positivos El matemático italiao Girolamo
(finitas o infinitas)
 Series ifiitas. SUCESIONES: Es u cojuto de úmeros: a,a a, dispuestos e u orde defiido y que guarda ua determiada ley de formació, que se expresa por ua formula Sucesió fiita: umero itado de térmios:, 5,8-5.
Series ifiitas. SUCESIONES: Es u cojuto de úmeros: a,a a, dispuestos e u orde defiido y que guarda ua determiada ley de formació, que se expresa por ua formula Sucesió fiita: umero itado de térmios:, 5,8-5.
1. Sucesiones y series numéricas
 ITINFORMÁTICA CÁLCULO INFINITESIMAL BOLETÍN CON SOLUCIONES DE LOS EJERCICIOS CURSO 005-06 Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3,
ITINFORMÁTICA CÁLCULO INFINITESIMAL BOLETÍN CON SOLUCIONES DE LOS EJERCICIOS CURSO 005-06 Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3,
Probabilidad FENÓMENOS ALEATORIOS
 Probabilidad FENÓMENOS ALEATORIOS E el mudo real hay feómeos regidos por leyes de tipo empírico (basadas e la experiecia), lógico o deductivo, e los que el efecto está determiado por ciertas causas. El
Probabilidad FENÓMENOS ALEATORIOS E el mudo real hay feómeos regidos por leyes de tipo empírico (basadas e la experiecia), lógico o deductivo, e los que el efecto está determiado por ciertas causas. El
1 Sucesiones. Ejemplos. a n = n a n = n! a n = n n. a n = p n. a n = 2n3 + n 2 + 5 n 2 + 8. a n = ln(n)
 1 Sucesioes De ició. Ua sucesió, a, es ua fució que tiee como domiio el cojuto de los úmeros aturales y como cotradomiio el cojuto de los úmeros reales: a : N! R. Se usa la siguiete otació: a () = a :
1 Sucesioes De ició. Ua sucesió, a, es ua fució que tiee como domiio el cojuto de los úmeros aturales y como cotradomiio el cojuto de los úmeros reales: a : N! R. Se usa la siguiete otació: a () = a :
1. Calcular, aplicando mentalmente la definición de raíz (no usar calculadora):
 EJERCICIOS de RADICALES º ESO académicas FICHA : Cocepto de raíz -ésima RECORDAR: Defiició de raíz -ésima: Caso particular de simplificació: a x x a x x (Añadir estas fórmulas al formulario, juto co la
EJERCICIOS de RADICALES º ESO académicas FICHA : Cocepto de raíz -ésima RECORDAR: Defiició de raíz -ésima: Caso particular de simplificació: a x x a x x (Añadir estas fórmulas al formulario, juto co la
Objetivos partir de su. nte de una función, Relacionar ASÍN CON CLA 11.4.
 CONTENIDOS.- MAPA CONCEPTUAL DE LA UNIDAD....- CONCEPTO DE LÍMITE DE UNA FUNCIÓNN EN UN PUNTO....- LÍMITES LATERALES: CARACTERIZACIÓN....- LÍMITES Y OPERACIONES CON FUNCIONES: ÁLGEBRA DE LÍMITES... 5.-
CONTENIDOS.- MAPA CONCEPTUAL DE LA UNIDAD....- CONCEPTO DE LÍMITE DE UNA FUNCIÓNN EN UN PUNTO....- LÍMITES LATERALES: CARACTERIZACIÓN....- LÍMITES Y OPERACIONES CON FUNCIONES: ÁLGEBRA DE LÍMITES... 5.-
AMPLIACIÓN DE MATEMÁTICAS APLICACIONES.
 AMPLIACIÓN DE MATEMÁTICAS APLICACIONES. Ejemplo 1. La ecuació poliómica x 2 + 2x + 2 = 0, co coeficietes reales, tiee dos solucioes complejas cojugadas: 1 + i y 1 i. Este o es u hecho aislado. Proposició
AMPLIACIÓN DE MATEMÁTICAS APLICACIONES. Ejemplo 1. La ecuació poliómica x 2 + 2x + 2 = 0, co coeficietes reales, tiee dos solucioes complejas cojugadas: 1 + i y 1 i. Este o es u hecho aislado. Proposició
Sucesiones y ĺımite de sucesiones
 Tema 3 Sucesioes y ĺımite de sucesioes Ídice del Tema Sucesioes........................................ 60 Progresioes....................................... 63 3 Covergecia......................................
Tema 3 Sucesioes y ĺımite de sucesioes Ídice del Tema Sucesioes........................................ 60 Progresioes....................................... 63 3 Covergecia......................................
DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN
 DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN Ídice. INTRODUCCIÓN2 2. SISTEMAS DE ECUACIONES LINEALES2 Defiicioes básicas.2 Iterpretació vectorial3
DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN Ídice. INTRODUCCIÓN2 2. SISTEMAS DE ECUACIONES LINEALES2 Defiicioes básicas.2 Iterpretació vectorial3
CAPITULO 2. Aritmética Natural
 CAPITULO Aritmética Natural Itroducció 1 Sumatorias Iducció Matemática Progresioes Teorema del Biomio 1. Coteidos. Itroducció 1) Asumiremos que el cojuto de úmeros reales R, +,, ) es u cuerpo ordeado completo.
CAPITULO Aritmética Natural Itroducció 1 Sumatorias Iducció Matemática Progresioes Teorema del Biomio 1. Coteidos. Itroducció 1) Asumiremos que el cojuto de úmeros reales R, +,, ) es u cuerpo ordeado completo.
UNIDAD 1 PROCESOS INFINITOS Y LA NOCIÓN DE LÍMITE
 UNIDAD PROCESOS INFINITOS Y LA NOCIÓN DE LÍMITE Propósitos. Explorar diversos problemas que ivolucre procesos ifiitos a través de la maipulació tabular, gráfica y simbólica para propiciar u acercamieto
UNIDAD PROCESOS INFINITOS Y LA NOCIÓN DE LÍMITE Propósitos. Explorar diversos problemas que ivolucre procesos ifiitos a través de la maipulació tabular, gráfica y simbólica para propiciar u acercamieto
Análisis de Señales en Geofísica
 Aálisis de Señales e Geofísica 3 Clase Frecuecia de los Sistemas Lieales e Ivariates Facultad de Ciecias Astroómicas y Geofísicas, Uiversidad Nacioal de La Plata, Argetia Fucioes y Valores Propios Defiició:
Aálisis de Señales e Geofísica 3 Clase Frecuecia de los Sistemas Lieales e Ivariates Facultad de Ciecias Astroómicas y Geofísicas, Uiversidad Nacioal de La Plata, Argetia Fucioes y Valores Propios Defiició:
Qué es la estadística?
 Qué es la estadística? La estadística tiee que ver co la recopilació, presetació, aálisis y uso de datos para tomar decisioes y resolver problemas. Qué es la estadística? U agete recibe iformació e forma
Qué es la estadística? La estadística tiee que ver co la recopilació, presetació, aálisis y uso de datos para tomar decisioes y resolver problemas. Qué es la estadística? U agete recibe iformació e forma
1. Calcular, aplicando mentalmente la definición de raíz (no usar calculadora):
 EJERCICIOS de RADICALES º ESO FICHA : Cocepto de raíz -ésima RECORDAR: Defiició de raíz -ésima: Caso particular de simplificació: a x x a x x (Añadir estas fórmulas al formulario, juto co la lista de los
EJERCICIOS de RADICALES º ESO FICHA : Cocepto de raíz -ésima RECORDAR: Defiició de raíz -ésima: Caso particular de simplificació: a x x a x x (Añadir estas fórmulas al formulario, juto co la lista de los
TEMA 5: INTERPOLACIÓN
 5..- ITRODUCCIÓ TEMA 5: ITERPOLACIÓ Supogamos que coocemos + putos (x,y, (x,y,..., (x,y, de la curva y = f(x, dode las abscisas x k se distribuye e u itervalo [a,b] de maera que a x x < < x b e y k = f(x
5..- ITRODUCCIÓ TEMA 5: ITERPOLACIÓ Supogamos que coocemos + putos (x,y, (x,y,..., (x,y, de la curva y = f(x, dode las abscisas x k se distribuye e u itervalo [a,b] de maera que a x x < < x b e y k = f(x
Números complejos Susana Puddu
 Números complejos Susaa Puddu 1. El plao complejo. E el cojuto C = IR IR defiimos la suma y el producto de dos elemetos de C de la siguiete maera a, b + c, d = a + c, b + d a, b.c, d = ac bd, ad + bc Dejamos
Números complejos Susaa Puddu 1. El plao complejo. E el cojuto C = IR IR defiimos la suma y el producto de dos elemetos de C de la siguiete maera a, b + c, d = a + c, b + d a, b.c, d = ac bd, ad + bc Dejamos
Mó duló 21: Sumatória
 INTERNADO MATEMÁTICA 16 Guía del estudiate Mó duló 1: Sumatória Objetivo: Coocer y aplicar propiedades para el cálculo de sumatorias. Para calcular alguas sumatorias es ecesario coocer sus propiedades
INTERNADO MATEMÁTICA 16 Guía del estudiate Mó duló 1: Sumatória Objetivo: Coocer y aplicar propiedades para el cálculo de sumatorias. Para calcular alguas sumatorias es ecesario coocer sus propiedades
PRIMERA SESIÓN. l. Se considera la sucesión de números reales definida por la relación de recurrenc1a: U n+l = a Un + ~ U n-1, con n > O
 PRIMERA SESIÓN Problema N l. l. Se cosidera la sucesió de úmeros reales defiida por la relació de recurreca: U +l = a U + ~ U -, co > O Siedo: a y ~ úmeros fijos. Se supoe tambié coocidos los dos primeros
PRIMERA SESIÓN Problema N l. l. Se cosidera la sucesió de úmeros reales defiida por la relació de recurreca: U +l = a U + ~ U -, co > O Siedo: a y ~ úmeros fijos. Se supoe tambié coocidos los dos primeros
Aplicaciones del cálculo integral vectorial a la física
 Aplicacioes del cálculo itegral vectorial a la física ISABEL MARRERO epartameto de Aálisis Matemático Uiversidad de La Lagua imarrero@ull.es Ídice 1. Itroducció 1 2. Itegral doble 1 2.1. Motivació: el
Aplicacioes del cálculo itegral vectorial a la física ISABEL MARRERO epartameto de Aálisis Matemático Uiversidad de La Lagua imarrero@ull.es Ídice 1. Itroducció 1 2. Itegral doble 1 2.1. Motivació: el
1 SISTEMA DE NUMEROS COMPLEJOS
 UNIVERSIDAD DEL VALLE FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMATICAS Prof DORIS HINESTROZA SISTEMA DE NUMEROS COMPLEJOS Sea C el cojuto de parejas ordeadas (a, b) deúmeros reales, esto es C = {(a, b)
UNIVERSIDAD DEL VALLE FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMATICAS Prof DORIS HINESTROZA SISTEMA DE NUMEROS COMPLEJOS Sea C el cojuto de parejas ordeadas (a, b) deúmeros reales, esto es C = {(a, b)
Unidad 1: Números Complejos
 Uidad 1: Números Complejos 11 Itroducció Además de los cojutos de úmeros aturales, eteros, racioales y reales existe el cojuto de úmeros complejos que juega u rol importate o solo e matemáticas sio e las
Uidad 1: Números Complejos 11 Itroducció Además de los cojutos de úmeros aturales, eteros, racioales y reales existe el cojuto de úmeros complejos que juega u rol importate o solo e matemáticas sio e las
Expresiones Algebraicas
 Semiario Uiversitario Matemática Módulo Expresioes Algebraicas Difícilmete se pueda estudiar cualquier rama de la matemática actual si u maejo algebraico razoable. Usamos la palabra maejo y o la de estudio,
Semiario Uiversitario Matemática Módulo Expresioes Algebraicas Difícilmete se pueda estudiar cualquier rama de la matemática actual si u maejo algebraico razoable. Usamos la palabra maejo y o la de estudio,
Convolución. Dr. Luis Javier Morales Mendoza. Procesamiento Digital de Señales Departamento de Maestría DICIS - UG
 Covolució Dr. Luis Javier Morales Medoza Procesamieto Digital de Señales Departameto de Maestría DICIS - UG Ídice.. Itroducció... Aálisis de Sistemas Discretos Lieales e Ivariates e el Tiempo.... Técicas
Covolució Dr. Luis Javier Morales Medoza Procesamieto Digital de Señales Departameto de Maestría DICIS - UG Ídice.. Itroducció... Aálisis de Sistemas Discretos Lieales e Ivariates e el Tiempo.... Técicas
IES Fco Ayala de Granada Sobrantes de 2005 (Modelo 3) Solución Germán-Jesús Rubio Luna OPCIÓN A
 IES Fco Ayala de Graada Sobrates de 005 (Modelo 3) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO _A ( putos) Dibuje el recito defiido por las siguietes iecuacioes: + y 6; 0 y; / + y/3 ; 0; ( puto) Calcule
IES Fco Ayala de Graada Sobrates de 005 (Modelo 3) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO _A ( putos) Dibuje el recito defiido por las siguietes iecuacioes: + y 6; 0 y; / + y/3 ; 0; ( puto) Calcule
Cálculo para la ingeniería Tomo II. Salvador Vera
 Cálculo para la igeiería Tomo II Salvador Vera 9 de eero de 5 ii Copyright c by Salvador Vera Ballesteros, 998-4. Ídice geeral 7. Series Numéricas 7.. El sigo del sumatorio: Sigma Σ... 7... Propiedades
Cálculo para la igeiería Tomo II Salvador Vera 9 de eero de 5 ii Copyright c by Salvador Vera Ballesteros, 998-4. Ídice geeral 7. Series Numéricas 7.. El sigo del sumatorio: Sigma Σ... 7... Propiedades
