Algunos temas de Cálculo para el Grado en Ingeniería Informática
|
|
|
- Rosa María Ruiz Poblete
- hace 6 años
- Vistas:
Transcripción
1 Alguos temas de Cálculo para el Grado e Igeiería Iformática José Rodríguez Ruiz Departameto de Igeiería y Tecología de Computadores Uiversidad de Murcia v.0 (8 de eero de 07)
2
3 Coteidos Itroducció V. Sucesioes.. Propiedades básicas Límites Sucesioes divergetes Resolució umérica de ecuacioes Itegrales 69.. Propiedades básicas y Regla de Barrow Cálculo de primitivas Itegrales impropias Aproximació mediate métodos uméricos Apédice: Iterpolació Series Propiedades básicas Series e itegrales Otros criterios de covergecia Series de Taylor Bibliografía
4
5 Itroducció Estas otas está destiadas a ayudar a los alumos de la asigatura CÁLCULO del Grado e Igeiería Iformática de la Uiversidad de Murcia. Tiee su orige e uestra experiecia docete e la asigatura, iiterrumpida desde su implatació e el curso 009/0 hasta el pasado curso 05/6. El material icluye explicacioes teóricas (co ejemplos y alguas demostracioes) y ejercicios resueltos (más de cie). Segú el pla de estudios de la titulació, los coteidos de la asigatura so: sucesioes de úmeros reales, resolució umérica de ecuacioes, series uméricas, aproximació local de fucioes, aproximació global de fucioes y cálculo itegral. E estas otas hemos optado por agrupar los coteidos e tres grades bloques o temas (sucesioes, itegrales y series), divididos a su vez e distitas leccioes.
6
7 Capítulo Sucesioes «OBJETIVOS» Distiguir etre sucesioes defiidas explícita o recursivamete. Utilizar la iducció para el estudio de sucesioes. Maejar las propiedades básicas de los límites. Estudiar la covergecia de sucesioes recursivas secillas. Determiar el orde de magitud de ua sucesió. Resolver ecuacioes uméricamete (método de bisecció). Este primer capítulo se dedica a las SUCESIONES de úmeros reales. Las sucesioes so u istrumeto muy valioso e Matemáticas y se utiliza de maera atural e Iformática. Por ejemplo, al aalizar teóricamete la eficiecia de u algoritmo, se le asocia ua sucesió cuyo térmio geeral t es el tiempo de ejecució de dicho algoritmo cuado el cojuto de datos de etrada es de tamaño. Es importate determiar la velocidad de crecimieto (orde de magitud) de t cuado crece. Este orde de magitud se suele utilizar para comparar algoritmos que resuelve u mismo problema. E la Lecció. explicamos cómo las sucesioes se puede defiir explícita o recursivamete y presetamos su clasificació e térmios de acotació y mootoía. Tambié recordamos el método de demostració por iducció y lo utilizamos para estudiar sucesioes defiidas recursivamete. E la Lecció. itroducimos las sucesioes covergetes y estudiamos propiedades básicas de los límites, como la regla del sadwich. Presetamos el teorema de covergecia de sucesioes que so simultáeamete acotadas y moótoas, utilizádolo para aalizar la covergecia de sucesioes defiidas recursivamete.
8 Sucesioes E la Lecció.3 estudiamos las sucesioes divergetes a ifiito. Para la resolució de idetermiacioes os apoyamos e la regla de L Hôpital para el cálculo de límites de fucioes de ua variable real. Nos cetramos e la comparació asitótica de sucesioes divergetes a ifiito. Establecemos ua jerarquía de ifiitos y explicamos cómo determiar el orde de magitud de ua sucesió. Fialmete, la Lecció.4 está dedicada a presetar el método de bisecció para la resolució aproximada de ecuacioes. Ates damos alguas herramietas para localizar y separar raíces de ecuacioes, como el Teorema de Bolzao.
9 . Propiedades básicas 3.. Propiedades básicas Coteidos Sucesioes defiidas explícita o recursivamete. Sucesioes acotadas y sucesioes moótoas. Método de iducció. Teoría Comezamos la lecció recordado el cocepto de sucesió de úmeros reales: Defiició... Ua sucesió de úmeros reales es ua aplicació a : N R. a a... a... Se represeta mediate los símbolos: (a ) N, [a ] N ó simplemete a. Los úmeros reales a,a,...,a,... se llama térmios de la sucesió. Por ejemplo, alguas sucesioes secillas so: [,4,6,8,...] (úmeros aturales pares), a =. [,,,...] (ua sucesió costate), a =. [,0,,0,,0,,0,...], a = si es impar, a = 0 si es par. Ua sucesió se puede defiir de dos formas:. EXPLÍCITAMENTE. Dado la expresió explícita de su térmio geeral. Por ejemplo: [,4,6,8,...] tiee térmio geeral a =. [,0,,0,...] tiee térmio geeral a = + ( )+.. POR RECURRENCIA. Expresado cada térmio e fució de los ateriores y dado los térmios iiciales ecesarios. Por ejemplo: [!,!,3!,4!,...] se defie como a =, a = a para todo.
10 4 Sucesioes [,,, 3, 5, 8, 3,,...] (sucesió de Fiboacci) se defie como a = a =, a = a + a para todo 3. A cotiuació vamos a clasificar las sucesioes e fució de dos criterios: acotació y mootoía. Comezamos co las sucesioes acotadas: Defiició... Se dice que ua sucesió a está: (i) acotada iferiormete si existe ua costate k R tal que k a para todo N; (ii) acotada superiormete si existe ua costate K R tal que a K para todo N; (iii) acotada si está acotada iferior y superiormete, es decir, si existe ua costate M R tal que a M para todo N. Veamos alguos ejemplos de sucesioes acotadas y o acotadas: Acotada: [,, 3, 4,...], co térmio geeral a = ( ). No acotada superiormete: [,3,5,7,9,...], co térmio geeral a =. No acotada iferiormete: [,, 4, 8, 6,...], a =. No acotada iferiormete i superiormete: [,, 3,4, 5,6,...], co térmio geeral a = ( ). A veces, cuado queremos estudiar propiedades (por ejemplo, la acotació) de ua sucesió que está defiida por recurrecia, coveiete utilizar el método de iducció, que recordamos a cotiuació: Es u coteido de la asigatura del primer cuatrimestre Fudametos Lógicos de la Iformática.
11 . Propiedades básicas 5 DEMOSTRACIONES POR INDUCCIÓN Cómo se demuestra que ua propiedad P() es cierta para todo N? PASO.- Se demuestra que: la propiedad es cierta cuado =. PASO.- Se demuestra que: SI se supoe que la propiedad es cierta para, ENTONCES tambié es cierta para +. Veamos u par de ejemplos ilustrado el método: Ejemplo..3. Demostramos por iducció que la sucesió a defiida por a = 3 a = a + para todo cumple a 3 para todo N. Por tato, a está acotada. Demostració. PASO.- Para = teemos a = 3 por defiició, así que evidetemete a 3. PASO.- Vamos a demostrar que: Si a 3 etoces a + 3. E efecto, teemos: a 3 = a 3 = + a Como a + = a +, deducimos que 3 a + 5. Teiedo e cueta que 3 y 5 3, cocluimos que a + 3, como se quería demostrar e el PASO. Esto completa la demostració por iducció. Ejemplo..4. Demostramos por iducció que la sucesió a defiida por a = a = a + para todo cumple a para todo N. Por tato, a o está acotada superiormete.
12 6 Sucesioes Demostració. PASO.- Para = teemos a = por defiició, así que evidetemete a. PASO.- Vamos a demostrar que: Si a etoces a + +. E efecto, teemos: a = a = a + +. Como a + = a +, la última desigualdad os dice que a + +. Claramete, teemos + +, luego a + +, como se quería demostrar e el PASO. Esto completa la demostració por iducció. Fializamos la lecció itroduciedo el cocepto de sucesió moótoa: Defiició..5. Se dice que ua sucesió a es: (i) moótoa creciete si a a + para todo N; (ii) moótoa estrictamete creciete si a < a + para todo N; (iii) moótoa decreciete si a a + para todo N; (iv) moótoa estrictamete decreciete si a > a + para todo N. Por ejemplo: [, 3, 5, 7, 9,...] es moótoa estrictamete creciete; [,, 3, 3, 5, 5,...] es moótoa decreciete pero o estrictamete; [,, 3, 4,...] o es moótoa creciete i decreciete. Observació..6. (i) Toda sucesió moótoa creciete está acotada iferiormete. (ii) Toda sucesió moótoa decreciete está acotada superiormete. El método de iducció tambié puede ser útil a la hora de estudiar la mootoía de sucesioes defiidas por recurrecia. Veámoslo co las sucesioes de los Ejemplos..3 y..4. Ejemplo..7. Demostramos por iducció que la sucesió a defiida por a = 3 a = a + para todo cumple a > a + para todo N. Por tato, a es moótoa estrictamete decreciete.
13 . Propiedades básicas 7 Demostració. PASO.- Para = teemos a = 3 y a = 3 + = 5, luego a > a. PASO.- Vamos a demostrar que: Si a > a + etoces a + > a +. E efecto, teemos: a > a + = a > a + = a + = a + > a + + = a +. Luego a + > a +, como se quería demostrar e el PASO. Esto completa la prueba por iducció. Ejemplo..8. Demostramos por iducció que la sucesió a defiida por a = a = a + para todo cumple a + > a para todo N. Por tato, a es moótoa estrictamete creciete. Demostració. PASO.- Para = teemos a = y a = + = 3, luego a > a. PASO.- Vamos a demostrar que: Si a + > a etoces a + > a +. E efecto, teemos: a + > a = a + > a = a + + > a +. Teiedo e cueta que a + = a + y a + = a + +, deducimos que a + > a +. La demostració ha fializado. Ejercicios Ejercicio..9. Demuestra por iducció las siguietes igualdades: ( + ) (i) =. (ii) ( ) =. (iii) + r + r + r r = r+, para todo r. r SOLUCIÓN. (i) La demostració por iducció se divide e dos pasos:
14 8 Sucesioes PASO.- Para = la igualdad es cierta evidetemete. PASO.- Demostramos que: Si = (+) etoces ( + ) = (+)(+). E efecto, basta observar que ( + ) = ( ) + ( + ) = ( + ) = lo que completa la demostració. + ( + ) = (ii) El PASO de la demostració es imediato. ( + ) + ( + ) = ( + )( + ), PASO.- Vamos a demostrar que: Si ( ) = etoces ( ) + ( + ) = ( + ). E efecto: ( ) + ( + ) = como se quería demostrar. = ( ( )) + ( + ) = + ( + ) = ( + ), (iii) La demostració por iducció se divide e dos pasos: PASO.- Para = la igualdad es cierta, ya que r (r + )(r ) = = r +. r r PASO.- Vamos a demostrar que: Si + r + r r = r+ r etoces + r + r r + = r+ r. E efecto, podemos hacerlo como e los apartados ateriores: + r + r r + r + = ( + r + r r ) + r + = = r+ r + r+ = (r+ ) + r + (r ) = r+ r r, lo que fializa la demostració. Ejercicio..0. Ecuetra ua fórmula explícita para el térmio geeral de las siguietes sucesioes: [,5,8,,4,...] [, 3, 5, 7, ] [ 9,..., 3 4, 7 8, 5 6, 3 ] [, 3,...,3, 4,5, 6 ],...
15 . Propiedades básicas 9 SOLUCIÓN. Los térmios geerales so respectivamete: a = + 3( ), b = ( )+, c =, d = si es impar si es par. Ejercicio... Determia si las siguietes sucesioes so acotadas o moótoas: a = b = + ( ) c = + ( ) d = se + ( + ) e = l SOLUCIÓN. Claramete, la sucesió a es moótoa estrictamete decreciete. Los primeros térmios de b so [ 0, 3, 3, 5 4, 4 5,...], luego b o es moótoa. La sucesió c es moótoa estrictamete creciete, ya que + lo es y la fució f (x) = x es estrictamete creciete e [0,). La sucesió d es moótoa estrictamete decreciete, ya que + lo es y la fució f (x) = sex es estrictamete creciete e el itervalo [0, ]. Fialmete, la sucesió e es moótoa estrictamete decreciete, ya que + = + lo es y la fució f (x) = lx es estrictamete creciete e (0,). Ejercicio... Se cosidera la sucesió a del Ejemplo..4, defiida por: a =, a = a + para todo. Demuestra por iducció que a = para todo N. SOLUCIÓN. La demostració por iducció se divide e dos pasos: PASO.- Para = teemos a = por defiició, así que a =. PASO.- Vamos a demostrar que: Si a = etoces a + = +. E efecto, por la fórmula de recurrecia teemos a + = a +. Utilizado la igualdad a =, deducimos que a + = a + = ( ) + = + + = +, como se quería demostrar e el PASO. Esto completa la prueba por iducció.
16 0 Sucesioes Ejercicio..3. La sucesió a está defiida por recurrecia: a = 0, a = 3, a = a 9 para todo 3. (i) Evalúa uos cuatos térmios de la sucesió y cojetura cuál es la expresió explícita de su térmio geeral. (ii) Demuestra por iducció que dicha expresió coicide co a para todo N. SOLUCIÓN. (i) Evaluado los primeros térmios, teemos: a = 0, a = 3, a 3 = a 9 = 0, a 4 = a 9 = 7 = ( ) 3 3 a 5 = a 3 9 = 0, a 6 = a 4 9 = ( ) = ( ) 3 5, Parece etoces que los térmios de la sucesió cumple: a = 0 y a = ( ) 3 para todo N. (ii) Vamos a demostrar por iducció que, efectivamete, la cojetura del apartado (i) es cierta. Distiguimos dos casos: térmios impares y térmios pares. Térmios impares: Vamos a demostrar por iducció que a = 0 para todo N. o ) Para = se cumple a = 0, por defiició. o ) Demostramos que: Si a = 0 etoces a (+) = a + = 0. E efecto, basta utilizar la fórmula de recurrecia: a + = a 9 = 0 9 = 0. Térmios pares: Vamos a demostrar por iducció que a = ( ) 3 para todo N. o ) Para = teemos, por defiició, que a = 3 = ( )0 3. o ) Demostramos que: Si a = ( ) 3 etoces a (+) = a + = ( ) 3 De uevo, basta utilizar la fórmula de recurrecia: a + = a 9 = ( ) 3 3 = ( )
17 . Propiedades básicas Por tato, la cojetura que hemos hecho e el apartado (i) es cierta. Ejercicio..4. La sucesió a está defiida por recurrecia: a =, a = a para todo. (i) Evalúa uos cuatos térmios de la sucesió y cojetura cuál es la expresió explícita de su térmio geeral. (ii) Demuestra por iducció que dicha expresió coicide co a para todo N. SOLUCIÓN. (i) Los primeros térmios de la sucesió so: [,, 6, 4, 0,... ], así que cojeturamos que el térmio geeral es!. (ii) Vamos a demostrar por iducció que a = para todo N.! PASO.- Para = teemos a = por defiició, así que a =!. PASO.- Vamos a demostrar que: Si a =! etoces a + = ( + )!. E efecto, por la fórmula de recurrecia teemos a + = a. Utilizado la igualdad + a =, deducimos que! a + = a + =! + = ( + )!, como se quería demostrar e el PASO. Esto completa la prueba por iducció. Ejercicio..5. Se cosidera la sucesió a defiida recurretemete por: a =, a = para todo. a (i) Demuestra por iducció que a para todo N. (ii) Demuestra que es moótoa estrictamete decreciete. SOLUCIÓN. (i) La demostració por iducció se divide e dos pasos: PASO.- Para = teemos a = por defiició, así que a.
18 Sucesioes PASO.- Vamos a demostrar que: Si a etoces a +. E efecto, teemos: a = a = a = a. Como a + = a, deducimos que a + 3, luego a +, como se quería demostrar e el PASO. Esto completa la demostració por iducció. (ii) Vamos a demostrar por iducció que a + < a para todo N. PASO.- Para = teemos a = y a = = 3, así que a < a. PASO.- Demostramos que: Si a + < a etoces a + < a +. E efecto: a + < a a + >0 = a + > a = a + < a = a + < a. Pero a + = a + y a + = a, luego a + < a +, fializado el PASO. Hemos demostrado así que a + < a para todo N, es decir, la sucesió es moótoa estrictamete decreciete. Ejercicio..6. Se cosidera la sucesió a defiida recurretemete por: a =, a = para todo. 3 a (i) Demuestra por iducció que 0 a para todo N. (ii) Demuestra que es moótoa estrictamete decreciete. SOLUCIÓN. (i) La demostració por iducció se divide e dos etapas: PASO.- Para = teemos a = por defiició, así que 0 a. PASO.- Vamos a demostrar que: Si 0 a etoces 0 a +. E efecto, teemos: 0 a = 0 a = 3 3 a = 3 3 a. Como a + = 3 a, deducimos que 3 a +, luego 0 a +, como se quería demostrar e el PASO. Esto completa la demostració por iducció.
19 . Propiedades básicas 3 (ii) Vamos a demostrar por iducció que a + < a para todo N. PASO.- Para = teemos a = y a = 3 a =, así que a < a. PASO.- Demostramos que: Si a + < a etoces a + < a +. E efecto: 3 a a + < a = a + > a = 3 a + > 3 a >0 = <. 3 a + 3 a Como a + = y a + =, deducimos que a + < a +, lo que fializa el 3 a + 3 a PASO. Hemos demostrado así que a + < a para todo N, es decir, a es moótoa estrictamete decreciete. Ejercicio..7. Se cosidera la sucesió defiida recurretemete por: a =, a = a para todo. Demuestra que es moótoa estrictamete creciete y acotada. SOLUCIÓN. Comezamos demostrado que es moótoa estrictamete creciete. Vamos a probar por iducció que a < a + para todo N. PASO.- Para = teemos a = y a = a =, así que a < a. PASO.- Demostramos que: Si a < a + etoces a + < a +. E efecto: a < a + = a < a + = a + = a < a + = a +, ya que la fució x es estrictamete creciete. Esto fializa el PASO y queda demostrado que la sucesió a es moótoa estrictamete creciete. Ahora vamos a demostrar que a está acotada. Como es moótoa creciete, está acotada iferiormete. Para ver que está acotada superiormete, comezamos evaluado
20 4 Sucesioes alguos térmios: a = a = a 3 = a 4 = a 5 = a 6 = a 7 = a 8 = a 9 = a 0 = E vista de los resultados, podemos cojeturar que a < para todo N. Vamos a demostrarlo por iducció. PASO.- Para = teemos a = <, claramete. PASO.- Demostramos que: Si a < etoces a + <. E efecto: multiplicado por la desigualdad a < obteemos a < 4 y, como la fució x es estrictamete creciete, cocluimos a + = a < 4 =, como se quería demostrar e el PASO. Esto prueba que la sucesió está acotada. Ejercicio..8. Se cosidera la sucesió a defiida por a = 0, a = y a = a + a para todo 3. (i) Demuestra por iducció que a a = ( ) para todo. (ii) Utiliza el apartado (i) para demostrar que la sucesió a es moótoa estrictamete creciete. (iii) Utiliza el apartado (i) para demostrar que la sucesió a es moótoa estrictamete decreciete.
21 . Propiedades básicas 5 SOLUCIÓN. (i) La demostració se hace e dos pasos: PASO.- Para = teemos a = y a = 0 por defiició, así que a a = = ( ) 0. PASO.- Demostramos que: Si a a = ( ) etoces a + a = ( )+. E efecto: a + a = a + a a = a + a a = a + a = = ( ) a a = ( ) ( )+ =. Esto fializa el PASO y completa la demostració por iducció. (ii) Vamos a demostrar que a < a + para todo N. Para ello observamos que a + a = a + a a = a + a a luego a + > a, como se quería demostrar. = a a = (i) = ( ) (iii) Ahora vamos a demostrar que a > a + para todo N. E efecto: a + a = a + + a luego a + < a. a = a + + a a = > 0, = a + a = (i) = ( )+ = < 0,
22 6 Sucesioes.. Límites Coteidos Covergecia y límite de sucesioes. Regla del Sadwich. Mootoía, acotació y covergecia. Teoría E esta lecció estudiamos el cocepto de límite de ua sucesió: Defiició... Decimos que L R es el límite de la sucesió a si para todo ε > 0 existe u ε N tal que a L < ε para todo ε. E tal caso, decimos que la sucesió coverge (o es covergete) a L, y escribimos lím a = L. Observació... La codició a L < ε es equivalete a L ε < a < L + ε. Observació..3. Sea a ua sucesió. Etoces a coverge a 0 a coverge a 0. Las sucesioes covergetes más secillas so: Ejemplo..4. Toda sucesió costate, digamos a = c, es covergete y lím a = c. La sucesió a = es covergete, co límite 0. La covergecia y el límite de ua sucesió o depede de sus primeros térmios, sólo de lo que ocurre a partir de u térmio. Más cocretamete:
23 . Límites 7 Observació..5. (i) Sea a ua sucesió. Las siguietes afirmacioes so equivaletes:. a es covergete;. para cada k N, la sucesió a +k = [a k+,a k+,...] es covergete; 3. existe k N tal que la sucesió a +k = [a k+,a k+,...] es covergete. E tal caso, lím a = lím a +k para todo k N. (ii) Sea a y b dos sucesioes. Si existe 0 N tal que a = b para todo > 0, etoces a coverge si y sólo si b coverge. E tal caso, lím a = lím b. La siguiete proposició explica lo que ocurre cuado realizamos operacioes aritméticas co sucesioes. Proposició..6. Sea a y b dos sucesioes covergetes, co límites a y b, respectivamete. Etoces: (i) a + b coverge a a + b; (ii) αa coverge a αa para cualquier α R; (iii) a b coverge a ab; (iv) si b 0, etoces b 0 a partir de cierto térmio y a b coverge a a b. Veamos ahora qué ocurre co los límites y las desigualdades: Proposició..7. Sea a y b dos sucesioes covergetes. (i) Si a b para todo N, etoces lím a lím b. (ii) (Regla del Sadwich) Si ua sucesió c cumple a c b para todo N y además lím a = lím b, etoces c es covergete y Ejemplo..8. Las sucesioes lím a = lím c = lím b. a = 0, c =! y b = cumple a c b para todo N. Así, por la Regla del Sadwich, lím! = 0.
24 8 Sucesioes Demostració. Es evidete que a = 0 c =!. Por otro lado, teemos c = b. Veamos ahora que, dado cualquier, se cumple c < b. E efecto, podemos escribir: c =! ( ) = } {{} factores =. Como 0 < k para todo k =,,...,, deducimos que y multiplicado por > 0 esta desigualdad obteemos ( c = ) = b, como se quería demostrar. El siguiete resultado es útil para detectar sucesioes covergetes a 0. Proposició..9. Si la sucesió a está acotada y la sucesió b coverge a 0, etoces la sucesió a b coverge a 0. Ejemplo..0. La sucesió a = se está acotada, porque Como la sucesió b = sex para todo x R. se coverge a 0, deducimos que lím = lím a b = 0. Vamos a establecer las relacioes que existe etre las ocioes de acotació y mootoía estudiadas e la lecció aterior y la oció de covergecia. Es secillo demostrar que toda sucesió covergete está acotada. Si embargo, hay sucesioes acotadas que o so covergetes, como [,0,,0,,0,...]. E cambio, sí so covergetes las sucesioes que so a la vez acotadas y moótoas:
25 . Límites 9 Teorema... (i) Toda sucesió covergete está acotada. (ii) Toda sucesió moótoa y acotada es covergete. Ejemplo.. (Sucesioes geométricas covergetes). Llamamos sucesió geométrica a ua sucesió de la forma a = r, dode r R es u úmero fijo. Se cumple: (i) Si r =, etoces r es costate, r = para todo N. (ii) Si 0 < r <, etoces r es moótoa estrictamete decreciete. (iii) Si r <, etoces r es covergete y lím r = 0. Demostració. (i) Es imediato. (ii) Para cualquier N teemos r + = r r < r, ya que r > 0 y r <. (iii) El caso r = 0 es evidete (e este caso, la sucesió r es costate, igual a 0). Supoemos ahora que r 0. Por el apartado (i) aplicado a la sucesió b = r, sabemos que b es moótoa estrictamete decreciete. E particular, 0 < b b = r para todo N, luego b está acotada. Por el Teorema.., b es covergete. Sea L = lím b. Como se cumple b + = r + = r r = r b para todo N y la sucesió b + tambié tiee límite L (véase la Observació..5), deducimos L = lím b + = lím r b = r lím b = r L. Es decir, L = r L. Esta ecuació equivale a 0 = r L L = ( r )L, de dode se deduce que L = 0 (porque r = ). Por tato, lím r = 0. Como r = r para todo N, cocluimos que la sucesió r tambié es covergete a 0 (véase la Observació..3) Ejemplo..3. E los Ejemplos..3 y..7 vimos que la sucesió a defiida por a = 3 a = a + para todo
26 0 Sucesioes es moótoa estrictamete decreciete y acotada. Por tato, es covergete. Vamos a demostrar que lím a =. Demostració. Sea L = lím a. Como se cumple a + = a + para todo N y la sucesió a + tambié tiee límite L (véase la Observació..5), deducimos ( a ) L = lím a + = lím + = lím a + = L +, luego L = L +. Resolviedo esta ecuació, obteemos L =. Es frecuete costruir sucesioes evaluado fucioes sobre los térmios de otra sucesió. Para estudiar la covergecia de sucesioes defiidas de esta forma, teemos: Proposició..4. Sea: a ua sucesió covergete a L R, f ua fució cotiua defiida e u itervalo abierto I, co L I. Etoces la sucesió f (a ) (que está defiida a partir de cierto térmio) coverge a f (L). Ejemplo..5. Cosideramos la sucesió a =, que es covergete a, y la fució f (x) = lx, que está defiida y es cotiua e el itervalo (0,). La sucesió ( ) f (a ) = l está defiida sólo para (ya que a = 0). Por la Proposició..4, teemos véase la Figura.. ( ) lím l = lím f (a ) = f ( ) ( = l = l, )
27 . Límites Figura.: Gráficas de la fució f (x) = lx y la sucesió a() =. Ejercicios Ejercicio..6. Para cada ua de las siguietes codicioes, ecuetra la expresió del térmio geeral de ua sucesió que la cumpla, o bie justifica que tal sucesió o puede existir: (i) lím a = 3 y a < 3 para todo N. (ii) lím a = y a > 3 a partir de u térmio. (iii) lím a = y a < 5 4 para todo N. (iv) lím a = 0 y a o es moótoa. SOLUCIÓN. (i) La sucesió a = 3 cumple los requisitos. (ii) Cualquier sucesió a covergete a satisface que a > 3 a partir de u térmio. (iii) No existe igua sucesió e tales codicioes, ya que si ua sucesió covergete a cumple a < 4 5 para todo N, etoces su límite satisface lím a 5 4 (véase la Proposició..7). (iv) La sucesió a = ( ) cumple los requisitos.
28 Sucesioes Ejercicio..7. Sea P(x) = A p x p + A p x p A x + A 0 Q(x) = B q x q + B q x q B x + B 0 dos poliomios de grados p y q, respectivamete, co q. Se cosidera las sucesioes a = P() y b = Q(). Demuestra que: (i) b 0 a partir de cierto térmio; (ii) a b coverge a 0 si p < q; (iii) a b coverge a A p B p si p = q. SOLUCIÓN. (i) Existe u 0 N tal que b = Q() 0 para todo > 0, porque Q(x) tiee sólo u úmero fiito de raíces ( es u poliomio o ulo!). (ii) Fijamos > 0 y e el cociete a b = A p p + A p p A + A 0 B q q + B q q B + B 0 dividimos umerador y deomiador por q, obteiedo: p a A p = b q + A p B q q q + B q p q q q Por otro lado, para cualquier k N teemos A q + A 0 q = B q + B 0 q A p = q p + A p q p A q + A 0 q. (.) B q + B q B q + B 0 q lím k = lím ( ) k ( = lím ) k = 0, así que la sucesió del umerador de (.) coverge a 0 (porque q > p), mietras que la sucesió del deomiador de (.) coverge a B q 0. Por tato a lím = 0 = 0. b B q
29 . Límites 3 (iii) Se razoa como e el apartado (ii), observado que e este caso (q = p) la sucesió que aparece e el umerador de (.) coverge a A p. Ejercicio..8. Justifica por qué las siguietes sucesioes so covergetes y calcula su límite: ( 7 ) ( + 6)se(!) 4 cos SOLUCIÓN. La sucesió ( 7 9) coverge a 0, ya que es ua sucesió geométrica y 7 9 = 7 9 < (Proposició..). Por otro lado, segú el Ejercicio..7, teemos lím 3 = 3 y lím + + = 0. La sucesió se(!) está acotada, ya que sex para todo x R. Como además lím 4 = 0 (Ejercicio..7), podemos aplicar la Proposició..9 para + 6 deducir ( + 6)se(!) lím 4 = 0. Fialmete, teiedo e cueta que lím = 0 y que la sucesió cos está acotada (porque cosx para todo x R), obteemos cos lím = 0 (aquí aplicamos de uevo la Proposició..9). Ejercicio..9. Demuestra que la sucesió l(!) l lím l(!) (l) = 0. SOLUCIÓN. Fijamos arbitrario. Observamos que está acotada y deduce que l(!) = l( ) = l + l l = l } +... {{ + l } ( )l, sumados ya que lk l para todo k =,..., (la fució lx es creciete). Por tato: 0 < l! ( )l = l l <.
30 4 Sucesioes Esto demuestra que la sucesió l(!) está acotada. l Por tato, como lím = 0, podemos aplicar la Proposició..9 para deducir que l como se quería demostrar. lím l(!) (l) = lím l(!) l l = 0, Ejercicio..0. Utiliza la Regla del Sadwich para calcular el límite de las sucesioes cuyos térmios geerales so: (i) (ii) SOLUCIÓN. (i) Para todo N se cumple: 7 = 7 < < = 7 = 7 Como lím = lím / = 0 =, resulta que lím 7 = 7. Fialmete, como la sucesió tiee sus térmios compredidos etre 7 y 7 y estas dos sucesioes coverge a 7, aplicado la Regla del Sadwich (Proposició..7) se deduce que: lím = 7. (ii) Para todo N, se observa que e la suma el meor sumado es Por otro lado, teemos }{{ + } sumados +, mietras que el mayor sumado es +, luego + < < +. lím + = 0 y lím + = 0
31 . Límites 5 (véase el Ejercicio..7). Por tato, la sucesió dada tiee todos sus térmios compredidos etre los de dos sucesioes covergetes a 0. Aplicado la Regla del Sadwich (Proposició..7) se obtiee que: [ lím ] = 0. Ejercicio... La sucesió a defiida recurretemete por a =, a = para todo. a es moótoa estrictamete decreciete y acotada (etre y ), véase el Ejercicio..5. Por tato, a es covergete. Cuáto vale lím a? SOLUCIÓN. Llamamos L = lím a. Como a para todo N, teemos las desigualdades L (véase la Proposició..7). Ahora, como a + = a para todo N y la sucesió a + tambié tiee límite L, se sigue que ) L = lím a + = lím ( a = = lím a L. Observamos que L = L L(L ) = L L + = 0 L =. Por tato, lím a =. Ejercicio... La sucesió a defiida recurretemete por a = a = para todo N 3 a es moótoa estrictamete decreciete y acotada (etre 0 y ), véase el Ejercicio..6. Por tato, a es covergete. Cuáto vale lím a?
32 6 Sucesioes SOLUCIÓN. Llamamos L = lím a. Como 0 a para todo N, teemos las desigualdades 0 L (Proposició..7). Teiedo e cueta que a + = 3 a para todo N y que la sucesió a + tambié tiee límite L, deducimos L = lím a + = lím = = 3 a 3 lím a 3 L, luego L = 3 L. Equivaletemete: L = 3 L L(3 L) = L + 3L = 0. Es decir, L es solució de la ecuació de segudo grado x 3x + = 0, cuyas dos solucioes so 3 ± 5. Co cuál de ellas coicide L? Por u lado, ya hemos visto que L. Por otro lado, > 3 + =, así que L = 3 5. Ejercicio..3. La sucesió a defiida recurretemete por a = a = a para todo es moótoa estrictamete creciete y acotada, véase el Ejercicio..7. Por tato, a es covergete. Cuáto vale lím a? SOLUCIÓN. Llamamos L = lím a. Teiedo e cueta la fórmula de recurrecia y que la sucesió a + tambié tiee límite L, deducimos ( ) L = lím a + = lím a = lím a = L, dode la igualdad ( ) se obtiee aplicado la Proposició..4 a la fució cotiua x. Por tato, L = L. Elevado al cuadrado esta igualdad, os queda L = L, o equivaletemete: L(L ) = 0. Como a para todo N (porque a es moótoa creciete y a = ), teemos L (Proposició..7) y, por tato, L =.
33 . Límites 7 Ejercicio..4. Se cosidera la sucesió b defiida recurretemete por: b =, b = b para todo. (i) Demuestra que b > para todo N. (ii) Demuestra que b es covergete a 0. SOLUCIÓN. (i) Por las propiedades de las fucioes expoeciales, sabemos que x > x > 0. Por tato, basta demostrar que b > 0 para todo N, y esto último se puede hacer imediatamete por iducció ( compruébalo!). (ii) Fijamos N. Se cumple b > (visto e el apartado (i)), luego <. Multiplicado esta última desigualdad por > 0, obteemos b + = b b <. Por tato: 0 < b + < para todo N. Como lím = 0, la Regla del Sadwich (Proposició..7) garatiza que la sucesió [b,b 3,...] es covergete a 0. Así que b tambié es covergete a 0. Ejercicio..5 (Sucesioes cotractivas). Se dice que ua sucesió a es cotractiva si existe ua costate 0 K < tal que a + a + K a + a para todo N. Se puede demostrar que toda sucesió cotractiva es covergete. Por ejemplo, so cotractivas todas las sucesioes a defiidas recurretemete por a = f (a ) dode f : [c,d] [c,d] es ua fució cotiua e el itervalo [c,d], derivable e (c,d) y tal que existe ua costate 0 K < cumpliedo f (x) K para todo x (c,d). Demuestra que las sucesioes siguietes so cotractivas: a = 0 b = a = cos(a ) para todo b = + b 3b + para todo
34 8 Sucesioes SOLUCIÓN. (i) La sucesió está defiida recurretemete por la fórmula a = f (a ), siedo f (x) = cosx. Teemos que f (x) [0,] para todo x [0,] y f (x) = sex = sex < se para todo x (0,). Por tato, eligiedo K = se, se cumple 0 < K < y f (x) < K para todo x (0,). Luego la sucesió a es cotractiva. (ii) La sucesió está defiida recurretemete por la fórmula b = f (b ), siedo f (x) = + x 3x +. Su derivada es f (x) = (3x + ) > 0 para todo x 3, así que f es estrictamete creciete e el itervalo ( 3,). Por tato: 6 7 = f () f (x) f (3) = 3 0 así que f (x) [,3] para todo x [,3]. Además: para todo x 3, f (x) = Por tato, b es cotractiva. (3x + ) < (3 + ) = < para todo x (,3). 49 Ejercicio..6. Se cosidera la sucesió a defiida por a = 0, a = y a = a + a para todo 3 (i) Demuestra que a es cotractiva (utiliza el apartado (i) del Ejercicio..8). (ii) Demuestra por iducció que a = a para todo. (iii) Calcula lím a. SOLUCIÓN. (i) Segú vimos e el Ejercicio..8, se cumple la igualdad Por tato: a + a + = = a a = ( ) para todo. = a + a para todo N, así que la sucesió a es cotractiva (podemos tomar K = ).
35 . Límites 9 (ii) La demostració se divide e dos pasos: PASO.- Para = teemos claramete a = = a. PASO.- Vamos a demostrar que: Si a = a etoces a + = a. E efecto, aplicado primero la fórmula de recurrecia y utilizado a cotiuació la igualdad a = a (dos veces, señaladas co (*)), teemos a + = a + a ( ) = ( a ) + a = + a ( ) = + ( a ) = a, como se quería demostrar e el PASO. Esto completa la prueba por iducció. (iii) Llamamos L = lím a. Como a + = a para todo N (segú hemos visto e el apartado (ii)) y la sucesió a + tambié tiee límite L, teemos ( L = lím a + = lím a ) = lím a De la igualdad L = L se obtiee imediatamete que L = 3. = L.
36 30 Sucesioes.3. Sucesioes divergetes Coteidos Sucesioes divergetes. Jerarquía de ifiitos. Órdees de magitud. Teoría Esta lecció se dedica a aalizar y comparar sucesioes co límite ifiito, segú su orde de magitud, que iformalmete podemos defiir como velocidad de crecimieto. Por ejemplo, el límite l lím = 0 (véase el Ejemplo.3.7) puede iterpretarse diciedo que la sucesió l se acerca a más letamete que la sucesió. Defiició.3.. Decimos que ua sucesió a es: (i) divergete si o es covergete; (ii) divergete a si para todo K R existe u K N tal que a > K para todo K ; e tal caso, escribimos lím a = ; (iii) divergete a si para todo K R existe u K N tal que e tal caso, escribimos lím a =. a < K para todo K ; Veamos alguos ejemplos secillos de sucesioes divergetes: a = es divergete a. a = 3 es divergete a. a = ( ) es divergete (pero o es divergete a i a ). Observació.3.. Sea a ua sucesió tal que a > 0 para todo N. Etoces:
37 .3 Sucesioes divergetes 3 lím a = 0 lím =. a El siguiete ejemplo completa el estudio de las sucesioes geométricas iiciado e el Ejemplo... Ejemplo.3.3 (Sucesioes geométricas divergetes). Sea r R. Se cumple: (i) Si r >, etoces lím r =. (ii) Si r, etoces r es divergete (pero o es divergete a i a ). Demostració. (i) La sucesió ( ) r = coverge a 0 porque 0 < < (Ejemplo..). Por r r tato, la sucesió r diverge a (véase la Observació.3.). (ii) Para ver que r o es covergete basta demostrar por iducció que r si es par, r si es impar. PASO.- Para = teemos r = r por hipótesis. PASO.- Vamos a demostrar dos cosas: (a) Si r etoces r +. E efecto: (.) r r = ( r) r = r + = r +. (b) Si r etoces r +. E efecto: r = r r = ( r) ( r ) = r +. Esto completa la demostració por iducció de (.). E la lecció aterior hemos visto que toda sucesió moótoa y acotada es covergete (Teorema..). Por otra parte, las sucesioes moótoas y o acotadas so divergetes a ó, como destacamos a cotiuació. Proposició.3.4. (i) Sea a ua sucesió moótoa creciete. Etoces: lím a = a o está acotada.
38 3 Sucesioes (ii) Sea b ua sucesió moótoa decreciete. Etoces: lím b = b o está acotada. La siguiete proposició permite aalizar la covergecia de sucesioes obteidas evaluado fucioes e los úmeros aturales. Proposició.3.5. Sea f ua fució defiida e u itervalo del tipo (c, ) tal que existe el límite lím x f (x) R {,}. Etoces la sucesió f () (que está defiida a partir de cierto térmio) cumple: (i) Si lím x f (x) = L R, etoces f () coverge a L. (ii) Si lím x f (x) =, etoces f () diverge a. (iii) Si lím x f (x) =, etoces f () diverge a. Figura.: Gráficas de la fució f (x) = x y la sucesió f () =. Sea a y b dos sucesioes, siedo al meos algua de ellas divergete a ó, o bie siedo ambas covergetes a 0. Si realizamos ciertas operacioes co ambas sucesioes (cociete, diferecia, etc.) y queremos estudiar la covergecia de la ueva sucesió, las reglas de la aritmética de límites fiitos (Proposició..6) deja de ser válidas y podemos ecotrar idetermiacioes, como explicamos a cotiuació.
39 .3 Sucesioes divergetes 33 INDETERMINACIONES Surge al estudiar lím (a b ) cuado lím a = lím b = ±. EJEMPLO: a = y b = l. 0 Surge al estudiar lím a b cuado lím a = 0 y lím b = ±. EJEMPLO: a = y b = l. a Surge al estudiar lím cuado lím a = ± y lím b = ±. b EJEMPLO: a = y b = l. 0 0 EJEMPLO: a = y b = l. a Surge al estudiar lím cuado lím b a = lím b = 0. Surge al estudiar lím a b cuado lím a = y lím b =. EJEMPLO: a = + y b =. 0 0 Surge al estudiar lím a b cuado lím a = lím b = 0. EJEMPLO: a = b =. Surge al estudiar lím a b cuado lím a = y lím b = 0. EJEMPLO: a = y b =. 0 El siguiete resultado, combiado co la Proposició.3.5, es muy útil para calcular límites de sucesioes resolviedo idetermiacioes. Teorema.3.6 (Regla de L Hôpital). Sea f y g dos fucioes derivables defiidas e u itervalo del tipo (c,), co g (x) 0 para todo x > c, tales que o bie lím x f (x) = lím x g(x) = 0 o bie lím x f (x) = ± y lím x g(x) = ±. f (x) f (x) Si existe el límite lím x g R {, }, etoces tambié existe lím (x) x g(x) y f (x) lím x g(x) = lím f (x) x g (x). Veamos u ejemplo dode se puede aplicar la Regla de L Hôpital:
40 34 Sucesioes l Ejemplo.3.7. Se cumple lím = 0. Demostració. Segú la Proposició.3.5, basta demostrar que lím vamos a hacer aplicado la Regla de L Hôpital a las fucioes f (x) = lx y g(x) = x, x x lx = 0. Esto lo que cumple lím x f (x) = lím x g(x) =. Derivado, teemos f (x) = x y g (x) =, luego f (x) lím x g (x) = lím x x = 0, lx y la Regla de L Hôpital asegura etoces que lím x x = 0. Fializamos la secció resolviedo alguas idetermiacioes co ayuda del límite calculado e el Ejemplo.3.7. Ejemplo.3.8. Se cumple: Demostració. lím ( l) = y lím =. (i) Llamamos a = l. Etoces: ( a lím = lím l = lím l ) l = lím =. E particular, existe u 0 N tal que a > para todo > 0. Equivaletemete: a > para todo > 0. Como la sucesió es divergete a, la desigualdad aterior garatiza que lím a =. (ii) Llamamos b = = / y defiimos c = l(b ). Por las propiedades de los logaritmos, teemos c = l. Por tato, lím c = 0. Y como la fució e x es cotiua, deducimos lím ec = e 0 = (véase la Proposició..4). Esto completa la prueba, ya que b = e l(b ) = e c.
41 .3 Sucesioes divergetes 35 E la seguda parte de la lecció os cetramos e la comparació de sucesioes divergetes a. Defiició.3.9. Ua sucesió a es mucho meor que otra sucesió b si se cumple: E tal caso, escribimos a b. a lím = 0. b Observació.3.0. Si a b y b c, etoces a c. Es decir, es ua relació trasitiva. El teorema siguiete resume las relacioes que se da etre las pricipales sucesioes divergetes a. Como cosecuecia, por ejemplo, teemos: l / = ! Teorema.3. (Jerarquía de Ifiitos). Para todo 0 < c < d y todo < r < s se cumple: Demostració. l c l c d r s! Vamos a calcular el límite de fucioes lx lím x x c utilizado la Regla de L Hôpital (Teorema.3.6). Derivado y tomado límites: lím x x = lím cxc x cx c = c lím x x c = c 0 = 0, lx luego lím x x c = 0. E virtud de la Proposició.3.5, lím l c = 0. c d porque d c > 0. E efecto: c lím d = lím d c = 0
42 36 Sucesioes d r E primer lugar, observamos que Vamos a calcular el límite de fucioes d ( ) d lím r = lím. (.3) r /d lím x x r x/d utilizado la Regla de L Hôpital (Teorema.3.6): lím x x = lím rx/d x lr d rx/d = 0. Por tato, lím = 0 (aplicamos la Proposició.3.5). Fialmete: r/d d ( (.3) ) d ( lím r = lím = r /d lím r /d ) d = 0 d = 0, ya que la fució x d es cotiua (aplicamos la Proposició..4). r s E efecto: r r ) lím s ( = lím = 0 s porque 0 < r < (véase el Ejemplo..). s s! Veamos e primer lugar que la sucesió a = s es covergete:! Teemos a + = s+ ( + )! = s s ( + )! = s + a < a s para todo N que cumpla > s (equivaletemete, + < ), ya que a > 0. Por tato, a es moótoa estrictamete decreciete a partir de u térmio. Como a > 0 para todo N, la sucesió a está acotada. Deducimos (por el Teorema..) que a es covergete a cierto L R. Además: ( ) s L = lím a + = lím + a s = lím + lím a = 0 L = 0.
43 .3 Sucesioes divergetes 37 Así que lím a = 0, como se quería demostrar.! Esta relació ya se comprobó e el Ejemplo..8. La demostració del Teorema.3. ha fializado. Dadas dos sucesioes divergetes a ifiito, puede ocurrir que lo haga a la misma velocidad. E este setido, damos la siguiete defiició. Defiició.3.. Ua sucesió a es del mismo orde que otra sucesió b si se cumple: lím E tal caso, escribimos a b. a b = L R, co L 0. a Observació.3.3. Sea a y b dos sucesioes tales que existe el límite lím R. b Como la fució x es cotiua, podemos aplicar la Proposició..4 para deducir lím a = lím. Por tato: b a b a b a b. Defiició.3.4. Se llama orde de magitud de ua sucesió a otra sucesió del mismo orde cuya expresió sea lo más secilla posible. Veamos alguos ejemplos secillos ilustrado estas defiicioes. Ejemplo.3.5. (i) porque lím = 0. Luego el orde de magitud de es. (ii) 0l + porque 0l + l lím = 0 lím + = = 0. Luego el orde de magitud de 0l + es.
44 38 Sucesioes Observació.3.6. La relació es simétrica y trasitiva, es decir: (i) la codició a b es equivalete a b a ; (ii) si a b y b c, etoces a c. E la proposició siguiete recopilamos varias propiedades de la relació que será de utilidad al estudiar el orde de magitud de ua sucesió. Estas propiedades permite deducir el orde de magitud de sucesioes defiidas como sumas, productos o cocietes de sucesioes cuyo orde de magitud es coocido. Proposició.3.7 (Propiedades de la relació ser del mismo orde ). (o) Si a 0 a partir de cierto térmio, etoces a a αa para todo α R, α 0. (o) Si a a y b b, etoces: a b a b (o3) Si a b, etoces a + b b. (o4) Si a a y b b, etoces y a a. b b Demostració. a b a b. (o) Basta observar que lím a a = lím = 0 y lím αa a = lím α = α = 0. (o) Para el producto teemos lím a b a b = lím a a El cociete se razoa de forma similar. (o3) Se cumple lím a + b b = lím a + b a b ( ) = = lím a a lím b b 0. lím a + b = 0 + = 0,
45 .3 Sucesioes divergetes 39 dode la igualdad marcada co ( ) es cosecuecia de la cotiuidad de la fució x y la Proposició..4. (o4) Basta observar que ( ) a = a a b b a b. b Esto completa la demostració de la Proposició.3.7. A cotiuació ilustramos las propiedades (o) (o4) co ejemplos cocretos. Ejemplo.3.8. Determiamos el orde de magitud de las siguietes sucesioes: (i) 3l( ) + (ii) (iii) Solució. (i) Comezamos observado que l( ) = l. Por tato:! + 3 3l( ) 3l 3l lím = lím = lím = 3 lím l = 3 0 = 0. Luego 3l( ). La propiedad (o3) implica que 3l( ) +, mietras que la propiedad (o) os dice que. Por tato, 3l( ) + y el orde de magitud de la sucesió es. (ii) Vamos a determiar el orde de magitud del umerador y el deomiador. Para el umerador, observamos que 7 + lím 7/ = lím + 7 = 0, luego 7 + 7/. Por otro lado, el deomiador cumple / porque 4 5 = 5/ (usamos la propiedad (o3)). Ahora, para el cociete, (o) asegura que / 5/ =
46 40 Sucesioes y, por tato, el orde de magitud de la sucesió es. (iii) El umerador cumple! + por la propiedad (o3) y el hecho de que!, segú hemos visto e la Jerarquía de Ifiitos (Teorema.3.). Ahora, para el cociete, la propiedad (o) asegura que! + El orde de magitud de la sucesió es = 3. Ejercicios Ejercicio.3.9. Sea P(x) = A p x p + A p x p A x + A 0 Q(x) = B q x q + B q x q B x + B 0 dos poliomios de grados p y q, respectivamete (Q 0). Se cosidera las sucesioes a = P() y b = Q(). Demuestra que si p > q etoces: (i) a b diverge a si A p y B q tiee el mismo sigo; (ii) a b diverge a si A p y B q tiee distito sigo. [Véase el Ejercicio..7.] Ejercicio.3.0. Calcula los límites de las siguietes sucesioes: (a) (b) (c) l + 3 (d) ( ) (e) + ( ) / + + SOLUCIÓN. (a) Dividiedo el umerador y el deomiador etre, teemos: 7 7 lím = lím lím 5 + = lím 5 + = 5 = 0.
47 .3 Sucesioes divergetes 4 (b) Tato el umerador como el deomiador so sucesioes divergetes a, así que teemos ua idetermiació x. Vamos a calcular el límite de fucioes lím x x utilizado la Regla de L Hôpital (Teorema.3.6). Si derivamos y tomamos límites, se tiee: luego lím x l x = l lím x lím x x x = 0. x = l 0 = 0, Por tato, lím = 0 (aplicamos la Proposició.3.5). (c) El umerador y el deomiador so sucesioes divergetes a, así que teemos otra vez ua idetermiació lx. Vamos a calcular el límite de fucioes lím x x + 3x utilizado la Regla de L Hôpital (Teorema.3.6). Si derivamos y tomamos límites, se tiee: luego Por tato, lím lím x x x + 3 = lím x lím x x + 3x = 0, lx x + 3x = 0. l = 0 (aplicamos la Proposició.3.5). + 3 (d) Como lím + =, teemos ua idetermiació del tipo. Llamamos ( ) a = + y defiimos ( ) b = l(a ) = l + ( + Al itetar calcular lím b = lím l para todo 3. ), os ecotramos ate ua idetermiació 0, que podemos trasformar e ua del tipo 0 0 escribiedo ( ) l + b =.
48 4 Sucesioes Ahora vamos a calcular el límite de fucioes ( ) x l x + lím x x utilizado la Regla de L Hôpital (Teorema.3.6). Derivado y tomado límites: lím x x + (x ) (x + ) x x + x 3 = lím x + x x x 3x = lím x x + x = 3, (.4) luego el límite de (.4) vale 3. Por tato, lím b = 3 (aplicamos la Proposició.3.5). Fialmete, como a = e b y la fució e x es cotiua, podemos usar la Proposició..4 para deducir que lím a = e lím b = e 3. + (e) Como lím + = y lím = 0, teemos ua idetermiació del tipo 0. Defiimos ( ( ) ) + / l + + a = y b = l(a ) =. + ( ) + l + Vamos a calcular lím b = lím. Tato el umerador como el deomiador so sucesioes divergetes a, así que teemos ua idetermiació del tipo. Para resolverla, vamos a calcular el límite de fucioes ( x ) + l x + lím x x mediate la Regla de L Hôpital (Teorema.3.6). Derivado y tomado límites: lím x x(x + ) (x + ) (x + ) x + x + = lím x x + x x 3 + x + x + = 0 = 0, (.5)
49 .3 Sucesioes divergetes 43 luego el límite (.5) vale 0. Por tato, lím b = 0 (aplicamos la Proposició.3.5). Fialmete, como a = e b y la fució e x es cotiua, podemos usar la Proposició..4 para deducir que lím a = e lím b = e 0 =. El siguiete criterio es otra herramieta útil para resolver idetermiacioes de la forma y 0 0 : Criterio de Stolz. Sea a y b dos sucesioes de úmeros positivos tales que y supogamos que: a + a lím = l R {, } b + b o bie lím a = lím b = 0 y b es moótoa estrictamete decreciete, o bie lím b = y b es moótoa estrictamete creciete. a Etoces lím = l. b Ejercicio.3.. Calcula los siguietes límites utilizado el Criterio de Stolz: l (a) lím k (b) lím r co r > y k N (c) lím 3/ SOLUCIÓN. (a) Tomamos a = l y b =, que es moótoa estrictamete creciete y diverge a. Como ( ) a + a l( + l + lím = lím b + b ( + ) = lím l = l = 0, l podemos aplicar el Criterio de Stolz para cocluir que lím = 0. (b) Vamos a demostrar que lím = 0 por iducció e k N. r PASO.- Para k =, tomamos a = y b = r, que es moótoa estrictamete creciete y diverge a. Como k a + a ( + ) lím = lím b + b r + r = lím (r )r = 0, podemos usar el Criterio de Stolz para deducir que lím r = 0.
50 44 Sucesioes k k+ PASO.- Demostramos que: Si lím = 0 etoces lím r r = 0. Defiimos a = k+ y b = r. Aplicado la fórmula del biomio de Newto: ( ) a + a = ( + )k+ k+ k+ b + b r + r = (r )r (k + )! j=0 j!(k + j)! j k+ = = k ( k (r )r j=0 (k + )! j!(k + j)! j ) = ( k j=0 (k + )! j!(k + j)!(r ) k j ) k r. a + a Como lím = 0, tomado límites cuado se obtiee lím = 0. El r b + b k+ Criterio de Stolz garatiza que lím r = 0. (c) Tomamos a = y b = 3/ (moótoa estrictamete creciete y divergete a ). Observamos que a + a + + (( + ) 3/ + 3/) = b + b ( + ) 3/ 3/ = ( + ) 3 3 = + (( + ) 3/ + 3/) = = ( + ) a + a Luego lím = a y, por el Criterio de Stolz, cocluimos que lím = b + b 3 b 3. Ejercicio.3.. Se cosidera la sucesió a defiida recurretemete por a =, a = a + + a para todo. + a (i) Demuestra que es moótoa estrictamete creciete. (ii) Demuestra que (iii) Demuestra por iducció que a > a + a > + [Idea: utiliza la desigualdad del apartado (ii).] para todo. para todo. +.
51 .3 Sucesioes divergetes 45 (iv) Deduce que a es divergete a. SOLUCIÓN. (i) Es secillo demostrar por iducció que a > 0 para todo N, así que a + a = + a + a > 0 para todo N. Luego a es moótoa estrictamete creciete. (ii) Para cualquier teemos a a = + a + a >, ya que ( + a ) = + a > + a. Por tato, a > a +. (iii) Vamos a demostrar por iducció que a > + para todo. PASO.- Para = teemos a = 5 3 > a + = 3. PASO.- Demostramos que: Si a > + etoces a + > +. E efecto: (ii) a + > a + > + + = +. Esto fializa la demostració. (iv) Como la sucesió b = + es divergete a y además se cumple la desigualdad a > b para todo, deducimos que a tambié es divergete a. Ejercicio.3.3. Determia el orde de magitud de las sucesioes siguietes y ordéalas segú dicho orde: (a) + (b) (d) (g) l( ) l l( + ) se(!) + (c) ( + 3)! l( ) + 3 (e) 3 3 (f) (h) SOLUCIÓN. Vamos a usar las propiedades (o) (o4) mecioadas e la Proposició.3.7. (a) Segú la Jerarquía de Ifiitos (Teorema.3.), teemos. Por la propiedad (o3), se cumple +. Orde de magitud:.
52 46 Sucesioes (b) Como se(!) es ua sucesió acotada y lím, teemos se(!) lím = 0 (véase la Proposició..9), es decir, se(!). Por la propiedad (o3), se cumple se(!) +. Fialmete, para el cociete, podemos aplicar la propiedad (o): se(!) +. Orde de magitud:. (c) Comezamos co el deomiador. Como se cumple l( ) = l 3 (porque l segú la Jerarquía de Ifiitos, Teorema.3.), la propiedad (o3) garatiza que l( ) Por otro lado, el umerador cumple ( + 3)! = ( + 3)( + )( + )! 3! ya que (+3)(+)(+) 3. Fialmete, para el cociete, la propiedad (o) implica Orde de magitud:!. ( + 3)! l( ) + 3 3! 3 =!. (d) El deomiador cumple +. Para determiar el orde de magitud del umerador, primero observamos que l( ) = ( )l l (ya que ). Por otro lado, se cumple + l l( ), luego + l( ) (por la propiedad (o4)). Aplicado (o3) teemos l( ) + + l( ). Para el cociete, la propiedad (o) garatiza que l( ) l( ) l = l.
53 .3 Sucesioes divergetes 47 Orde de magitud: l. (e) Podemos escribir 3 3 = ( 3 ) 3 = 8 3. Segú la Jerarquía de Ifiitos (Teorema.3.), teemos 3 8, así que 3 8. La propiedad (o3) os dice que Orde de magitud: 8. (f) Podemos sacar factor comú y escribir ( = ), 4 ya que 4. Orde de magitud:. (g) Calculamos el límite de fucioes lím x lx l(x + ) utilizado la Regla de L Hôpital (Teorema.3.6). Si derivamos y tomamos límites: lím x x x + x + = lím =, x x luego el límite (.6) vale. Aplicado la Proposició.3.5 obteemos y por tato lím l l( + ) = 0, l. Orde de magitud:. l( + ) (.6) (h) Claramete teemos /. Por otro lado, 3 = 3/ 0, así que (usamos (o3) y (o)). Ahora, para el cociete, (o) implica Orde de magitud: / / = / =. ORDENACIÓN.- Es secillo comprobar que los órdees de magitud obteidos satisface las relacioes siguietes: l / 8!
54 48 Sucesioes Por la propiedad (o4), las sucesioes origiales verifica las mismas relacioes: se(!) + l( ) El ejercicio está resuelto. l l( + ) ( + 3)! l( ) + 3 Ejercicio.3.4. Determia el orde de magitud de las sucesioes siguietes y ordéalas segú dicho orde: (a) (d) (g) ( )! + (b) 3 + l( ) (c) ( ) l( ) (e) 3 + ( 3) (f) cos l( ) ( + l)(l + ) (h) + SOLUCIÓN. Vamos a usar las propiedades (o) (o4) mecioadas e la Proposició.3.7. (a) Teemos /, ya que lím / = lím 5 = lím = 0. Como 3 3 = 3 3/, la propiedad (o3) implica /. Ahora podemos aplicar (o) para deducir / =. 3 3/ Orde de magitud:. (b) Razoado como e el apartado (a), obteemos: + + =. Por otro lado, l( ) = l l. La propiedad (o) garatiza ahora que + + l( ) l.
55 .3 Sucesioes divergetes 49 Orde de magitud: l. (c) Por u lado, teemos ( )!!, ya que ( )! lím = lím! = 0. Como! (Jerarquía de Ifiitos, Teorema.3.), deducimos que ( )!. La propiedad (o3) os asegura etoces que ( )! +. Por otro lado, Usado la propiedad (o), deducimos que Orde de magitud:. ( )! =. (d) Como 3 3 (Jerarquía de Ifiitos, Teorema.3.), la propiedad (o3) garatiza que Por otro lado, l( ) = l + l l. Ahora, podemos usar (o) para cocluir ( ) l( ) 3 l. Orde de magitud: 3 l. (e) Teemos 3 ( 3), ya que lím 3 ( 3) = lím ( ) = 0. 3 Por la propiedad (o3), 3 + ( 3) ( 3) 3. Orde de magitud: 3. cos (f) Como cos es ua sucesió acotada, teemos lím = 0 (véase la Proposició..9), es decir, cos. Utilizado (o3), deducimos que cos. Orde de magitud:. (g) Como l, teemos + l (usamos (o3)). Por otro lado, l + l. La propiedad (o) os garatiza que ( + l)(l + ) l y l( ) ( + l)(l + ) = l ( + l)(l + ) l l =. Orde de magitud:. (h) Claramete, +. Orde de magitud:. ORDENACIÓN.- Es secillo comprobar que los órdees de magitud obteidos satisface las relacioes siguietes: l 3 l 3.
56 50 Sucesioes Por la propiedad (o4), las sucesioes origiales verifica las mismas relacioes: l( ) ( + l)(l + ) cos l( ) + ( ) l( ) 3 + ( 3) ( )! Ejercicio.3.5. Demuestra que ( + )l( + ) l l. SOLUCIÓN. Teemos ( + )l( + ) l = ( l( + ) l ) + l( + ) = ( ) + = l + l( + ) = l ( Como lím + = e, resulta que lím ) l ( + )l( + ) l l( + ). [( + ) ] + l( + ). [( + ) ] = le = y, por tato, l Por otro lado, segú vimos e el apartado (g) del Ejercicio.3.3, lím l( + ) =, luego l l( + ) y así como se quería demostrar. ( + )l( + ) l l, Ejercicio.3.6. Los tiempos de ejecució de dos algoritmos que resuelve el mismo problema co datos de etrada so y , respectivamete. Qué algoritmo es más rápido para valores grades de? SOLUCIÓN. Como (Jerarquía de Ifiitos, Teorema.3.), el algoritmo más rápido para valores grades de es el que tiee tiempo de ejecució Ejercicio.3.7. U computador procesa datos e segudos. Alterativamete, ua preparació previa de los datos, que tarda hora, permite procesar datos e (+)l segudos. Iteresa la preparació para valores grades de?
57 .3 Sucesioes divergetes 5 SOLUCIÓN. U método permite procesar datos e a = segudos, mietras que el otro lo hace e b = ( + )l segudos ( sumamos el tiempo de preparació!). Como 3600 ( + ) l, aplicado (o3) teemos b ( + )l l (ya que + ). Por otro lado, segú la Jerarquía de Ifiitos (Teorema.3.) se cumple l, luego l. Aplicado (o4) deducimos que b a. Esto idica que, para valores grades de, iteresa hacer la preparació previa de los datos. Ejercicio.3.8. Si depositamos u capital C e u baco, a u tipo de iterés aual I, el capital resultate después de años es: (a) co iterés simple: (b) co iterés compuesto: a 0 = C, a = a +C b 0 = C, b = b I 00 ( + I ) 00 para todo, para todo. Deduce co cuál de las dos fórmulas el capital resultate crece más rápido, dado el orde de magitud de cada ua de ellas. SOLUCIÓN. Se puede demostrar fácilmete por iducció ( hazlo!) que ( a = C + I ) 00 ( y b = C + I ) 00 para todo = 0,,,..., luego a y b r, siedo r = + 00 I >. Segú la Jerarquía de Ifiitos (Teorema.3.), teemos r y, por tato, a b (aquí aplicamos la propiedad (o4) de la Proposició.3.7). Así, el capital resultate crece más rápido co la fórmula del iterés compuesto. Ejercicio.3.9. Sea a el úmero de istruccioes de u determiado algoritmo para su ejecució sobre datos de etrada. Dicho algoritmo actúa del siguiete modo: Co u sólo dato de etrada resuelve el problema co ua istrucció.
58 5 Sucesioes Se pide: Co datos de etrada usa 4 istruccioes para reducir el problema a datos y después se ejecuta el mismo algoritmo sobre estos datos. (a) Defie la sucesió recurrete a. (b) Estudia la mootoía y acotació de a. (c) Demuestra que a < para todo N. (d) Deduce que lím =. (e) Determia el orde de magitud de a. a SOLUCIÓN. (a) La sucesió a está defiida por la fórmula de recurrecia: a = a = 4 + a para todo. (b) Se cumple a + = 4+a > a para todo N, luego a es moótoa estrictamete creciete. E particular, a para todo N. Por lo tato, teemos la desigualdad a = 4 + a 4 + para todo, de dode se deduce que la sucesió a o está acotada superiormete. Luego lím a =. (c) Vamos a realizar la demostració por iducció. PASO.- Para = es evidete que a <. PASO.- Vamos a demostrar que: Si a < etoces a + ( + ) < ( + ). E efecto, por la fórmula de recurrecia, teemos: a + ( + ) = 4 + a ( + ) = 4 + a 4 = = a ( ) a + < + = ( + ), dode (*) es cosecuecia de la desigualdad triagular. Esto completa la prueba. (d) Dividiedo etre la desigualdad del apartado (c), teemos a < para todo N. Recordamos que la desigualdad triagular afirma que u + v u + v para todo u,v R.
59 .3 Sucesioes divergetes 53 Esta última desigualdad y la Regla del Sadwich (Proposició..7) garatiza que lím a a = 0, es decir, lím =. (e) Por el apartado (d), a, así que a tiee orde de magitud.
60 54 Sucesioes.4. Resolució umérica de ecuacioes Coteidos Existecia y uicidad de solucioes. Método de bisecció. Teoría Alguos problemas de ciecias experimetales e igeiería coduce a ecuacioes que o se puede resolver de forma exacta. Por ejemplo, ecuacioes como x x 5 x x 3 + 6x = 0, sex = x, e x = x, etc. E esta lecció vamos a estudiar cómo resolverlas de forma aproximada. Comezamos co ua breve descripció de las etapas a seguir: (0) Preparació de la ecuació. La ecuació se reescribe e la forma f (x) = 0, siedo f ua fució adecuada. [Las raíces de la ecuació so las abscisas de los putos del plao dode la gráfica de f corta al eje OX.] () Localizació y separació de las raíces. Se determia el úmero de raíces (solucioes) de la ecuació y, para cada raíz, se ecuetra u itervalo dode esté dicha raíz, pero dode o esté igua otra raíz. [Para ciertas ecuacioes, las etapas (0) y () se puede cambiar de orde.] () Aproximació de las raíces. Para cada raíz c de la ecuació, se halla valores cada vez más próximos al valor exacto de c, dado ua cota del error cometido e cada aproximació. Como algoritmo de aproximació osotros vamos a utilizar el método de bisecció, que geera ua sucesió de aproximacioes c 0,c,c,...,c,c +,... covergete a c. El siguiete teorema es muy útil para demostrar la existecia de raíces de ecuacioes del tipo f (x) = 0 e u itervalo. Teorema.4. (Bolzao). Sea f : [a, b] R ua fució cotiua tal que f (a) f (b) < 0. Etoces existe c (a,b) tal que f (c) = 0.
61 .4 Resolució umérica de ecuacioes 55 E otras palabras, el Teorema de Bolzao afirma que si f (a) y f (b) tiee sigos opuestos (bie f (a) > 0 y f (b) < 0, o bie f (a) < 0 y f (b) > 0), etoces la ecuació f (x) = 0 tiee al meos ua raíz e el itervalo (a,b). Veamos u ejemplo: Ejemplo.4.. Se cosidera la ecuació 3x 3 + x x =. Se cumple: la ecuació es equivalete a f (x) = 0, dode f (x) = 3x 3 + x x ; f (0) = < 0 y f () = > 0; por tato, la ecuació tiee al meos ua raíz e el itervalo (0,). Figura.3: Gráfica de la fució f (x) = 3x 3 + x x y raíz de la ecuació f (x) = 0. Para separar las raíces de ua ecuació del tipo f (x) = 0, ecesitamos decidir si u itervalo cotiee ua úica raíz. A cotiuació damos alguos criterios que ivolucra propiedades de crecimieto y covexidad de f. Observació.4.3. Si f es ua fució estrictamete creciete o decreciete, etoces la ecuació f (x) = 0 puede teer, como mucho, ua úica raíz. Proposició.4.4 (Uicidad de Raíces). Sea f : [a,b] R ua fució cotiua tal que f (a) f (b) < 0 y además cumple algua de las siguietes codicioes:
62 56 Sucesioes (i) f es estrictamete creciete (por ejemplo, si f (x) > 0 para todo x (a,b)), (ii) f es estrictamete decreciete (por ejemplo, si f (x) < 0 para todo x (a,b)), (iii) f es covexa (por ejemplo, si f (x) 0 para todo x (a,b)), (iv) f es cócava (por ejemplo, si f (x) 0 para todo x (a,b)). Etoces existe u úico c (a, b) tal que f (c) = 0. Demostració. Casos (i) y (ii). Se deduce de la Observació.4.3. Caso (iii). Vamos a demostrarlo por reducció al absurdo. Supogamos que existe c < c e el itervalo (a,b) cumpliedo f (c ) = f (c ) = 0. Distiguimos dos situacioes: f (a) > 0 y f (b) < 0. Etoces defiimos t = b c b c (0,). U secillo cálculo muestra que tc +( t)b = c. Como f es covexa, deducimos 0 = f (c ) = f (tc + ( t)b) t f (c ) + ( t) f (b) = ( t) f (b), es decir, 0 ( t) f (b), cotradiciedo que t > 0 y f (b) < 0. f (a) < 0 y f (b) > 0. Ahora defiimos t = c c c a (0,). Etoces ta + ( t)c = c. La covexidad de f os permite deducir 0 = f (c ) = f (ta + ( t)c ) t f (a) + ( t) f (c ) = t f (a), es decir, 0 t f (a), cotradiciedo que t > 0 y f (a) < 0. Fialmete, el caso (iv) se deduce imediatamete del (iii) aplicado a la fució f, que es covexa si f es cócava. La ecuació del Ejemplo.4. tiee ua úica raíz e el itervalo (0,), ya que e ese ejemplo f es covexa ( f (x) = 8x + 4 > 0 para todo x (0,)), véase la Figura.3. Ejemplo.4.5. Localizamos y separamos las raíces de la ecuació e x = x 3.
63 .4 Resolució umérica de ecuacioes 57 Figura.4: Gráfica de las fucioes g(x) = e x y h(x) = x 3. Solució. Primero observamos que e x = x 3 x 3 e x = x 3 e x = 0. Es decir, la ecuació es equivalete a f (x) = 0, siedo f la fució f (x) = x 3 e x. Calculamos su derivada: f (x) = 3x e x + x 3 e x = x e x (3 + x). Por tato, f (x) sólo se aula e x = 3 y x = 0, cumpliédose además: f (x) < 0 para todo x (, 3), f (x) > 0 para todo x ( 3,0), f (x) > 0 para todo x (0,). Luego f es estrictamete decreciete e (, 3] y estrictamete creciete e [ 3, ). Aplicado la Observació.4.3, deducimos que la ecuació f (x) = 0 tiee como mucho ua raíz e cada uo de los itervalos (, 3] y [ 3,). Para cualquier x 0, teemos x 3 0, mietras que e x > 0 (idepedietemete del sigo de x), luego x 3 e x 0 y por tato f (x) = x 3 e x < 0. Como cosecuecia, la ecuació f (x) = 0 o tiee raíces e el itervalo (,0], y tampoco e (, 3]!
64 58 Sucesioes Para buscar ua posible raíz e el itervalo (0,), vamos a evaluar la fució f e varios putos, buscado u cambio de sigo. Por ejemplo: f (0) = 0 3 e 0 = < 0 y f () = 3 e = e > 0. Por el Teorema de Bolzao.4., la ecuació f (x) = 0 tiee ua raíz e (0,). CONCLUSIÓN: la ecuació e x = tiee ua úica raíz. Además, dicha raíz está e x3 el itervalo (0,). Véase la Figura.4 e la págia 57. Ejemplo.4.6. Localizamos y separamos las raíces de la ecuació x = cosx. Solució. La ecuació es equivalete a f (x) = 0, siedo f la fució f (x) = x cosx. Observamos que f es ua fució par: f ( x) = ( x) cos( x) = x cosx = f (x). Por tato, u úmero c R es raíz de la ecuació si y sólo si lo es c. Así, bastará ecotrar las raíces positivas de la ecuació (si las hay). Para buscar ua posible raíz e el itervalo (0,), vamos a evaluar la fució f e varios putos, buscado u cambio de sigo. Por ejemplo: ( π ) ( π ) ( π ) f (0) = 0 cos0 = < 0 y f = cos = π 4 > 0. Por el Teorema de Bolzao.4., la ecuació f (x) = 0 tiee ua raíz e (0, π ). La derivada f (x) = x + sex es positiva para todo x (0, π ) (sex > 0 para todo x (0, π )). Por la Proposició.4.4, deducimos que la ecuació f (x) = 0 tiee ua úica raíz e (0, π ). Por otro lado: x π = ( π ) x > cosx = f (x) = x cosx > 0. Por tato, la ecuació f (x) = 0 o tiee raíces e el itervalo [ π,). CONCLUSIÓN: la ecuació x = cosx sólo tiee dos raíces, c y c. Además ( c = c, c 0, π ), c ( π ),0. Véase la Figura.5 e la págia 59.
65 .4 Resolució umérica de ecuacioes 59 Figura.5: Gráfica de las fucioes g(x) = x y h(x) = cosx. A cotiuació vamos a explicar e qué cosiste el MÉTODO DE BISECCIÓN para la aproximació de raíces de ecuacioes del tipo f (x) = 0. Los datos de etrada de este algoritmo so ua fució f y u itervalo [a,b], que debe cumplir las codicioes siguietes: f : [a,b] R es cotiua y f (a) f (b) < 0, la ecuació f (x) = 0 tiee ua úica raíz c (a, b). Los pasos del algoritmo so: PASO 0. Defiimos a 0 = a y b 0 = b. Calculamos c 0 = a 0+b 0 (el puto medio del itervalo [a 0,b 0 ]). Se puede dar 3 casos: Si f (c 0 ) = 0 etoces c 0 = c es la raíz de la ecuació. PARAMOS! Si f (c 0 ) f (a 0 ) < 0 etoces defiimos a = a 0 y b = c 0, y vamos al PASO. Si f (c 0 ) f (b 0 ) < 0 etoces defiimos a = c 0 y b = b 0, y vamos al PASO. PASO. Calculamos c = a +b (el puto medio del itervalo [a,b ]). Se puede dar 3 casos: Si f (c ) = 0 etoces c = c es la raíz de la ecuació. PARAMOS!
66 60 Sucesioes ETC. ETC. Si f (c ) f (a ) < 0 etoces defiimos a = a y b = c, y vamos al PASO. Si f (c ) f (b ) < 0 etoces defiimos a = c y b = b, y vamos al PASO. Mediate este algoritmo se geera ua sucesió de itervalos I = [a,b ] y ua sucesió c de aproximacioes de la raíz c, que cumple: I + está coteido e I y la logitud de I + es la mitad de la logitud de I ; c y c perteece a I. Se puede demostrar fácilmete por iducció que la logitud de I es b a. Observació.4.7. E la práctica, es ecesario dar algú criterio de parada para deteer el algoritmo (cuado f (c ) 0 e los sucesivos pasos). Por ejemplo, podemos fijar el úmero de pasos a realizar. E la proposició siguiete veremos que, dado cualquier ε > 0, siempre podemos ecotrar de forma efectiva u úmero de pasos tal que E esta desigualdad: c c < ε. c c es el error absoluto de c como aproximació de c; ε represeta el error absoluto máximo permitido. Proposició.4.8. (i) Para cada N se cumple las desigualdades: 0 c a b a 0 b c b a c c b a + (ii) Las sucesioes a, b y c coverge a c. (iii) Para cada ε > 0 se cumple: Demostració. c c < ε para todo > log ( b a ε ). (i) El puto c perteece al itervalo I = [a,b ]. Por tato, la distacia de c a cualquiera de los extremos de I es meor o igual que la logitud de I. Es decir: c a = c a b a y c b = b c b a.
67 .4 Resolució umérica de ecuacioes 6 Por otro lado, como c es el puto medio del itervalo I, la distacia etre c y c es meor o igual que la mitad de la logitud de I. Es decir: c c b a +. (ii) Como 0 c a b a b a y lím = 0, la Regla del Sadwich (Proposició..7) asegura que lím (c a ) = 0, luego lím a = c. La demostració de que las sucesioes b y c coverge a c es aáloga. (iii) Por u lado, teemos la desigualdad c c b a, y por otro lado: + ( ) ( ) b a b a ( ) > log + > log ε + > b a ε > b a ε ε +, ya que la fució x es estrictamete creciete. Vamos a ilustrar el método de bisecció co u ejemplo cocreto. Ejemplo.4.9. Aproximació de la raíz de la ecuació 3x 3 + x x = 0 e el itervalo [0,] (véase el Ejemplo.4.) mediate el método de bisecció. Solució. Aplicamos varios pasos del método de bisecció. PASO 0. Teemos: a 0 = 0 f (a 0 ) = < 0 b 0 = f (b 0 ) = > 0 c 0 = 0.5 f (c 0 ) =.5 < 0 Como f (c 0 ) f (b 0 ) < 0, elegimos a = c 0 = 0.5 y b = b 0 =. PASO. Teemos: a = 0.5 f (a ) =.5 < 0 b = f (b ) = > 0 c = 0.75 f (c ) = < 0 Como f (c ) f (b ) < 0, elegimos a = c = 0.75 y b = b =.
68 6 Sucesioes PASO. Teemos: a = 0.75 f (a ) = < 0 b = f (b ) = > 0 c = f (c ) = > 0 Como f (c ) f (a ) < 0, elegimos a 3 = a = 0.75 y b 3 = c = PASO 3. Teemos: a 3 = 0.75 f (a 3 ) = < 0 b 3 = f (b 3 ) = > 0 c 3 = 0.85 f (c 3 ) = > 0 Como f (c 3 ) f (a 3 ) < 0, elegimos a 4 = a 3 = 0.75 y b 4 = c 3 = Por ejemplo, tras 0 pasos obteemos c 0 = Si llamamos c a la raíz de la ecuació, el error absoluto de c 0 como aproximació de c verifica la acotació: segú hemos visto e la Proposició.4.8. c 0 c 0 = , Ejercicios Ejercicio.4.0. Se cosidera la ecuació e x = x. (i) Demuestra que tiee ua úica raíz y da u itervalo de logitud dode se ecuetre dicha raíz. (ii) A partir de dicho itervalo, cuátos pasos del método de bisecció so ecesarios para obteer ua aproximació de la raíz co error absoluto meor que 0.04? SOLUCIÓN. (i) La existecia de ua úica raíz se puede razoar gráficamete. La represetació gráfica de las fucioes e x y x e el itervalo [,] es
69 .4 Resolució umérica de ecuacioes 63 Detro del dibujo, las gráficas de ambas fucioes se corta e u úico puto, así que la ecuació e x = x tiee ua úica raíz e el itervalo (,). Como la fució e x es estrictamete creciete y la fució x es estrictamete decreciete, fuera del itervalo (,) las gráficas de ambas fucioes o se vuelve a cortar, es decir, la ecuació e x = x sólo tiee ua raíz. Esto tambié podemos demostrarlo aalíticamete. Observamos primero que la ecuació e x = x es equivalete a f (x) = 0, siedo f la fució f (x) = x e x. Calculamos su derivada: f (x) = e x. Como e x > 0 para todo x R, deducimos que f (x) < 0 para todo x R, luego la fució f es estrictamete decreciete e todo R y la ecuació f (x) = 0 tiee como mucho ua raíz (Observació.4.3). Veamos que, efectivamete, la ecuació tiee ua raíz. Como la fució f es cotiua y cumple f (0) = 0 e 0 = = > 0, f () = e = e < 0, el Teorema de Bolzao.4. garatiza que la ecuació f (x) = 0 tiee ua raíz e el itervalo (0,) (que tiee logitud ). (ii) Si llamamos c 0,c,...,c,... a las sucesivas aproximacioes que proporcioa el método de bisecció aplicado a la fució f e el itervalo [0,], y llamamos c a la úica raíz de la ecuació f (x) = 0, sabemos (véase la Proposició.4.8) que el error absoluto
70 64 Sucesioes de c como aproximació de c cumple: c c +. Teemos que ecotrar u tal que < Vamos probado co = 0,,,... y + observamos que = 4 ya la cumple ( 5 = 0.035). Por tato, basta 4 pasos del método de bisecció para obteer ua aproximació co error absoluto meor que Ejercicio.4.. Demuestra que todo poliomio de grado impar tiee, al meos, ua raíz. SOLUCIÓN. Sea P(x) = a x +a x +...+a x+a 0 u poliomio de grado impar. Sabemos que si a > 0 etoces mietras que si a < 0 etoces lím P(x) = y lím P(x) =, x x lím P(x) = y lím P(x) =. x x E cualquier caso, podemos ecotrar dos úmeros reales a < b tales que P(a)P(b) < 0. Como cualquier fució poliómica es cotiua, el Teorema de Bolzao.4. os dice que la ecuació P(x) = 0 tiee, al meos, ua raíz e el itervalo (a,b). Ejercicio.4.. Se cosidera la ecuació x 3 x + 3x 5 = 0. (i) Demuestra que tiee ua úica raíz y da u itervalo de logitud dode se ecuetre dicha raíz. (ii) A partir de dicho itervalo, cuátos pasos del método de bisecció so ecesarios para obteer ua aproximació de la raíz co error absoluto meor que 0 5? SOLUCIÓN. (i) La ecuació es de la forma f (x) = 0, siedo f la fució poliómica f (x) = x 3 x + 3x 5. Segú hemos visto e el Ejercicio.4., la ecuació tiee al meos ua raíz. Para localizarla, evaluamos f e varios putos buscado u cambio de sigo. Por ejemplo: f (0) = 5 < 0 y f () = > 0.
71 .4 Resolució umérica de ecuacioes 65 Por el Teorema de Bolzao.4., la ecuació f (x) = 0 tiee al meos ua raíz e el itervalo (0,). Para demostrar que sólo hay ua raíz, vamos a comprobar que f (x) = 3x 4x + 3 es positiva para todo x R. Efectivamete, la ecuació de segudo grado f (x) = 0 o tiee solucioes reales, así que f (x) o cambia de sigo e todo R. Como f (0) = 3 > 0, deducimos que f (x) > 0 para todo x R. Luego f es estrictamete creciete e todo R y así la ecuació f (x) = 0 sólo tiee ua raíz (Observació.4.3). (ii) Si llamamos c 0,c,...,c,... a las sucesivas aproximacioes que proporcioa el método de bisecció aplicado a la fució f e el itervalo [0,], y llamamos c a la úica raíz de la ecuació f (x) = 0, sabemos (Proposició.4.8) que el error absoluto de c como aproximació de c cumple: ( ) c c < 0 5 para todo > log Así que 7 pasos del método de bisecció sería suficietes para coseguir ua aproximació (c 7 ) de c co error absoluto meor que 0 5. Ejercicio.4.3. Demuestra que la ecuació l(x + ) e x cos(πx) = 0 tiee ifiitas raíces. SOLUCIÓN. Cosideramos la fució cotiua f (x) = l(x +) e x cos(πx). Observamos que para cada N se cumple: l( + ) + e f () = l( + ) e si es impar, si es par. Por otro lado, afirmamos que l(x + ) e x < 0 para todo x 0. E efecto, basta teer e cueta que la fució g(x) = l(x + ) e x cumple g(0) = l e 0 = y es estrictamete decreciete e el itervalo [0,), ya que g (x) = x x + ex < e x < 0 para todo x > 0 (la desigualdad x x + < equivale a (x ) > 0). Así, resulta que para cada N teemos l( + ) + e > 0 f () = l( + ) e < 0 si es impar, si es par.
72 66 Sucesioes Por el Teorema de Bolzao.4., la ecuació f (x) = 0 tiee al meos ua solució e cada uo de los siguietes itervalos: Por tato, la ecuació tiee ifiitas raíces. (,), (,3), (3,4),... Ejercicio.4.4. Se cosidera la ecuació xsex =. (i) Determia cuátas solucioes tiee. (ii) Demuestra que tiee ua úica solució e el itervalo [0, π ]. (iii) Cuátos pasos del método de bisecció so ecesarios para calcular aproximadamete dicha solució co error absoluto meor que 0.0? SOLUCIÓN. (i) La ecuació es equivalete a f (x) = 0, siedo f (x) = xsex. Para cada N, teemos ( ) ( )π ( )π > 0 si es impar, f = ( )π < 0 si es par. Como la fució f es cotiua, el Teorema de Bolzao.4. garatiza que la ecuació f (x) = 0 tiee al meos ua solució e cada uo de los siguietes itervalos: ( π, 3π ) ( 3π,, 5π ) ( 5π,, 7π Por tato, la ecuació f (x) = 0 tiee ifiitas solucioes. ),... (ii) Evaluado la fució, observamos que f (0) = < 0 y f ( π ) = π > 0, luego la ecuació f (x) = 0 tiee al meos ua solució e el itervalo (0, π ). Por otro lado, la derivada f (x) = sex + xcosx es positiva para todo x (0, π ), ya que ( sex > 0 y cosx > 0 para todo x 0, π ). Por tato, f es estrictamete creciete e [0, π ] y la ecuació f (x) = 0 tiee ua úica solució e (0, π ) (véase la Observació.4.3). (iii) Si llamamos c 0,c,...,c,... a las sucesivas aproximacioes que proporcioa el método de bisecció aplicado a la fució f e el itervalo [0, π ], y llamamos c a la úica
73 .4 Resolució umérica de ecuacioes 67 raíz de la ecuació f (x) = 0 e dicho itervalo, sabemos que el error absoluto de c como aproximació de c cumple: π c c + = π + π (véase la Proposició.4.8). Buscamos u N tal que < 0.0. Probado co + = 0,,... observamos que = 3 ya cumple la desigualdad. Por tato, basta 3 pasos del método para obteer ua aproximació co error absoluto meor que 0.0. Ejercicio.4.5. Determia cuátas solucioes tiee la ecuació x = sex. SOLUCIÓN. La ecuació equivale a f (x) = 0, eligiedo la fució f (x) = x sex. Su derivada cumple f (x) = cosx < 0 para todo x R (ya que cosx para todo x R), así que f es estrictamete decreciete e todo R y la ecuació f (x) = 0 puede teer, como mucho, ua solució e R (Observació.4.3). Por otro lado, f (0) = > 0 y f (π) = π < 0. Aplicado el Teorema de Bolzao.4. a la fució cotiua f e el itervalo [0, π], deducimos que la ecuació f (x) = 0 tiee ua solució e (0,π). Por lo tato, la ecuació tiee ua úica solució e R. Ejercicio.4.6. Demuestra que la ecuació x xsex cosx = 0 tiee exactamete dos raíces. SOLUCIÓN. E primer lugar, observamos que la fució f (x) = x xsex cosx es par. E efecto, como el seo (resp. coseo) es ua fució impar (resp. par), teemos f ( x) = ( x) ( x)se( x) cos( x) = x xsex cosx. Por tato, u úmero c R es raíz de la ecuació si y sólo si lo es c. Así, decir que la ecuació tiee exactamete dos raíces es equivalete a decir que sólo tiee ua raíz e el itervalo (0,) (claramete, 0 o es raíz, ya que f (0) = ). La derivada de f es f (x) = x sex xcosx + sex = x( cosx). Como cosx > 0 para todo x R, teemos f (x) > 0 para todo x > 0, luego f es estrictamete creciete e (0,) y así la ecuació f (x) = 0 sólo puede teer ua raíz e el itervalo (0,) (Observació.4.3).
74 68 Sucesioes Vamos a evaluar f e alguos putos buscado u cambio de sigo. Por ejemplo, f (0) = < 0 y ( π ) ( π ) π ( π ) ( π ) ( π ) f = se π cos = = π ( π ) > 0. El Teorema de Bolzao.4. asegura que existe ua raíz de la ecuació f (x) = 0 e (0, π ). Por tato, la ecuació tiee ua úica raíz e (0,). Ejercicio.4.7. Determia cuátas solucioes tiee la ecuació (x ) = lx. SOLUCIÓN. La ecuació es equivalete a f (x) = 0, siedo f (x) = (x ) lx. La derivada de esta fució es f (x) = (x ) x = x 4x. x Las solucioes de la ecuació x 4x = 0 so a = + 6 y b = 6, luego f (x) = (x a)(x b). x E vista de esta expresió, teiedo e cueta que a > 0 y b < 0, deducimos que f (x) < 0 si x (0,a), f (x) > 0 si x (a,). Por tato, f es estrictamete decreciete e (0, a] y estrictamete creciete e [a, ), así que la ecuació f (x) = 0 puede teer como mucho ua solució e cada uo de esos itervalos (Observació.4.3). Veamos que, efectivamete, las tiee. Evaluado, f (a) = < 0. Por otro lado, lím f (x) = lím f (x) =, así que x 0 x podemos elegir úmeros reales 0 < b < a y a < b tales que f (b ) > 0 y f (b ) > 0. Como f es cotiua, el Teorema de Bolzao.4. garatiza que la ecuació f (x) = 0 tiee solucioes e los itervalos (b,a) y (a,b ). Por tato, la ecuació f (x) = 0 tiee exactamete dos solucioes e (0,).
75 Capítulo Itegrales «OBJETIVOS» Coocer la iterpretació geométrica del cocepto de itegral. Aplicar la Regla de Barrow para el cálculo de itegrales. Calcular primitivas secillas. Estudiar la covergecia de itegrales impropias y calcular su valor. Utilizar métodos uméricos básicos para aproximar itegrales. Maejar técicas básicas de iterpolació para aproximar fucioes. Este segudo capítulo se cetra e el estudio de las INTEGRALES de fucioes reales de ua variable real. El cálculo itegral es ua herramieta fudametal e ciecias e igeiería. E Iformática, por ejemplo, se utiliza para estudiar el orde de magitud del tiempo de ejecució de ciertos algoritmos (como veremos e el capítulo siguiete). E la Lecció. itroducimos el cocepto de itegral de ua fució cotiua y lo iterpretamos geométricamete, e térmios de áreas. Además de las propiedades básicas de las itegrales, presetamos la Regla de Barrow como herramieta teórica para el cálculo de itegrales. E la Lecció. repasamos alguas primitivas imediatas y estudiamos dos técicas básicas de cálculo de primitivas: el cambio de variable (sustitució) y el método de itegració por partes. Tambié explicamos cómo calcular primitivas de fraccioes racioales secillas. E la Lecció.3 estudiamos el cocepto de itegral impropia de ua fució cotiua defiida e todo R o e u itervalo de la forma (,b] ó [a,). Estas itegrales impropias se va a utilizar e la asigatura del segudo cuatrimestre Estadística.
76 70 Itegrales La Lecció.4 está dedicada a presetar alguos métodos uméricos para el cálculo aproximado de itegrales. Cocretamete, os cetramos e los métodos del Trapecio y Simpso, como ejemplos de métodos de cuadratura. E dos aexos presetamos u par de métodos de Mote Carlo (como ejemplos de algoritmos probabilistas). E ciecias e igeiería, a la hora de calcular itegrales se utiliza métodos uméricos, ya que e la práctica calcular ua primitiva de la fució a itegrar suele ser mucho más costoso o icluso imposible. Como apédice al capítulo, e la Lecció.5 realizamos ua breve itroducció a la iterpolació (poliomial y a trozos). Las técicas de iterpolació so ua herramieta muy útil para aproximar fucioes globalmete y se aplica, por ejemplo, al cálculo aproximado de itegrales.
77 . Propiedades básicas y Regla de Barrow 7.. Propiedades básicas y Regla de Barrow Coteidos Sumas superiores e iferiores y defiició de la itegral. Propiedades básicas de la itegral. Regla de Barrow. Teoría Comezamos recordado el Teorema de Weierstrass. A lo largo de la lecció [a,b] es u itervalo cerrado y acotado de R. Teorema.. (Weierstrass). Sea f : [a, b] R ua fució cotiua. Etoces existe s 0,s [a,b] tales que f (s 0 ) f (x) f (s ) para todo x [a,b]. Escribimos f (s 0 ) = mí f ([a,b]) (valor míimo de f e [a,b]); f (s ) = máx f ([a,b]) (valor máximo de f e [a,b]). A cotiuació defiimos las sumas iferiores y superiores de ua fució cotiua utilizado el Teorema de Weierstrass.
78 7 Itegrales Defiició... Sea f : [a, b] R ua fució cotiua y N. Escribimos x k = a + k b a, k = 0,,...,. (i) Se llama -ésima suma iferior de f al úmero I ( f ) = b a mí f ( [x k,x k ] ). k= (ii) Se llama -ésima suma superior de f al úmero S ( f ) = b a máx f ( [x k,x k ] ). k= Si además f (x) 0 para todo x [a,b], etoces la suma iferior I ( f ) es ua aproximació por defecto del área del recito delimitado por la gráfica de f, el eje OX y las rectas x = a y x = b (véase la Figura.), mietras que la suma superior S ( f ) es ua aproximació por exceso de dicha área (véase la Figura. e la págia 73). Figura.: La suma iferior I 0 ( f ) de la fució f (x) = se(x ) e el itervalo [.7,0] es la suma de las áreas de los rectágulos verdes. El cálculo de las sumas superiores e iferiores es imediato cuado la fució es costate, creciete o decreciete, como observamos a cotiuació.
79 . Propiedades básicas y Regla de Barrow 73 Figura.: La suma superior S 0 ( f ) de la fució f (x) = se(x ) e el itervalo [.7,0] es la suma de las áreas de los rectágulos azules. Observació..3. Si f es costate co valor C R (es decir, f (x) = C para todo x [a,b]), etoces I ( f ) = S ( f ) = (b a)c para todo N. Demostració. E este caso teemos mí f ([x k,x k ]) = C para todo k =,...,, luego mí f ( [x k,x k ] ) = C y así k= I ( f ) = b a Para la suma superior el razoamieto es aálogo. Observació..4. Si f es creciete, etoces I ( f ) = b a mí f ( [x k,x k ] ) = (b a)c. k= f (x k ) y S ( f ) = b a k= Demostració. Basta observar que, como f es creciete, teemos para k = 0,,...,. f (x k ) para todo N. k= mí f ( [x k,x k ] ) = f (x k ) y máx f ( [x k,x k ] ) = f (x k )
80 74 Itegrales Observació..5. Si f es decreciete, etoces I ( f ) = b a f (x k ) y S ( f ) = b a k= f (x k ) para todo N. k= Demostració. Basta observar que, como f es decreciete, teemos para k = 0,,...,. mí f ( [x k,x k ] ) = f (x k ) y máx f ( [x k,x k ] ) = f (x k ) Las Figuras.3 y.4 ilustra gráficamete las observacioes ateriores. Figura.3: Sumas iferior y superior de f (x) = x e [0,] co =. Figura.4: Sumas iferior y superior de f (x) = cosx e [0, π ] co = 8.
81 . Propiedades básicas y Regla de Barrow 75 Ejemplo..6. Sea f : [0,] R la fució idetidad, es decir, f (x) = x para todo x [0,]. Etoces, para cada N, teemos: I ( f ) = Demostració. E este ejemplo [a,b] = [0,], así que y S ( f ) = +. x k = k para k = 0,,...,. Como f es creciete, podemos aplicar las fórmulas de la Observació..4 para obteer y I ( f ) = b a f (x k ) = k= S ( f ) = b a k=x k = f (x k ) = k= Por otro lado, es secillo demostrar que k = k= k= k=x k = k k= = (k ) = k (.) k= k. (.) k= = ( + ) k = k= para todo N. Utilizado esta fórmula e (.) y (.), obteemos I ( f ) = ( ) como se quería demostrar. = y S ( f ) = ( + ) = +, Estamos ya e codicioes de itroducir el cocepto de itegral: Se puede demostrar por iducció, véase el Ejercicio..9. Alterativamete: k= ( ) ( ) k = ( ) ( ) = = ( ) ( ) ( ) ( ) ( ) ( ) = ( + ) ( + ) = ( + ). }{{} sumados
82 76 Itegrales Teorema..7. Sea f : [a,b] R ua fució cotiua. Etoces las sucesioes I ( f ) y S ( f ) so covergetes y se cumple lím I ( f ) = lím S ( f ). Llamamos itegral de f e [a,b] a dicho límite, que se represeta mediate b a f ó b a f (x)dx. Además, I ( f ) b a f S ( f ) para todo N. Si f (x) 0 para todo x [a,b], etoces la itegral f es el área del recito compredido etre la gráfica de f, el eje OX y las rectas x = a y x = b. b a Ejemplo..8. Sea f : [a,b] R ua fució costate co valor C, es decir, f (x) = C para todo x [a,b]. Como I ( f ) = S ( f ) = (b a)c para todo N (véase la Observació..3), teemos: b a f (x)dx = (b a)c. Ejemplo..9. Sea f : [0,] R la fució idetidad, f (x) = x para todo x [0,]. Como I ( f ) = y S ( f ) = + (véase el Ejemplo..6), teemos: 0 f (x)dx = lím I ( f ) = lím = = lím + = lím S ( f ). A cotiuació presetamos dos propiedades básicas de la itegral que so bastate útiles a la hora de efectuar cálculos. Proposició..0 (Liealidad de la itegral). Sea f,g : [a,b] R dos fucioes cotiuas y sea α,β R. Etoces b a (α f + βg) = α b a f + β b a g.
83 . Propiedades básicas y Regla de Barrow 77 Proposició.. (Aditividad de la itegral). Sea f : [a,b] R ua fució cotiua y sea c (a,b). Etoces b a f = c a b f + f. c La preguta fudametal que se platea ahora es: Dada ua fució cotiua f : [a,b] R, cómo podemos calcular E geeral, trabajar co las sumas superiores e iferiores es complicado y para respoder a la preguta teemos dos posibilidades: ( a ) Aplicar la Regla de Barrow, calculado previamete ua primitiva de f, como veremos a cotiuació. ( a ) Utilizar métodos uméricos, obteiedo ua aproximació del valor exacto de la itegral, como veremos e la Lecció.4. Defiició... Sea f,f : I R dos fucioes defiidas e u itervalo I R. Decimos que F es ua primitiva de f e I si F es derivable e I y F (x) = f (x) para todo x I. Teorema..3 (Regla de Barrow). Sea f,f : [a,b] R dos fucioes. Si f es cotiua y F es ua primitiva de f e [a,b], etoces b Escribimos [ F(x) ] b = F(b) F(a). a a f = F(b) F(a). Veamos u par de ejemplos secillos ilustrado la Regla de Barrow. Ejemplo..4. Para calcular por ejemplo, F(x) = x. Aplicado la Regla de Barrow: como habíamos visto e el Ejemplo b xdx ecesitamos ua primitiva de f (x) = x e [0,], xdx = F() F(0) = 0 =, a f?
84 78 Itegrales Ejemplo..5. Para calcular por ejemplo, F(x) = x4. Aplicado la Regla de Barrow: 4 Ejercicios x 3 dx ecesitamos ua primitiva de f (x) = x 3 e [,], x 3 dx = F() F() = = 5 4. Ejercicio..6. Se cosidera la fució f (x) = x + e el itervalo [0,]. Calcula la suma iferior I 4 ( f ) y la suma superior S 4 ( f ). SOLUCIÓN. E este caso [a,b] = [0,] y = 4, así que x 0 = 0, x = 4, x =, x 3 = 3 4 y x 4 =. Como f es decreciete e el itervalo [0,], podemos aplicar las fórmulas de la Observació..5, obteiedo y 4 I 4 ( f ) = f (x k ) = 4 k= (( = ( ) ( + ) S 4 ( f ) = 4 4 f (x k ) = k= ( = 4 ( ( 0 + ) + ( ) ( + ) + ( ) ( + ) + 4 ( ) 3 + ) + ( + )) = ( ) ( + ) + ( ) 3 + )) = Ejercicio..7. Se cosidera la fució f (x) = x 3 e el itervalo [0,]. Calcula la suma iferior I 3 ( f ) y la suma superior S 3 ( f ). SOLUCIÓN. Trabajamos co [a, b] = [0, ] y = 3, así que los putos itermedios so x 0 = 0, x = 3, x = 4 3 y x 3 =. Como f es creciete e el itervalo [0,], las fórmulas de la Observació..4 os permite obteer I 3 ( f ) = 3 3 f (x k ) = k= 3 ( ( ) ( ) ) 4 3 = 6 3 9
85 . Propiedades básicas y Regla de Barrow 79 y S 3 ( f ) = 3 3 f (x k ) = k= 3 ( ( ) ( ) ) = Ejercicio..8. (i) Demuestra por iducció que = ( + )( + ) 6 para todo N. (ii) Se cosidera la fució f (x) = x e el itervalo [0,]. Co la ayuda de la fórmula del apartado (i), demuestra que (iii) Calcula I ( f ) = y S ( f ) = para todo N. 0 x dx utilizado las fórmulas del apartado (ii). (iv) Comprueba que F(x) = x3 3 es ua primitiva de f (x) = x e [0,] y utilízala para calcular 0 x dx mediate la Regla de Barrow. SOLUCIÓN. (i) Es evidete que la fórmula es valida para =. Vamos a demostrar ahora que: k ( + )( + ) = k= 6 E efecto, teemos: = + k = k= ( + )( + )(( + ) + ). 6 + k = k + ( + ) ( + )( + ) = + ( + ) = k= k= 6 ( + )( + ) + 6( + ) = = ( + )( ( + ) + 6( + ) ) 6 6 = = ( + )( ), 6
86 80 Itegrales y por otro lado ( + )(( + ) + ) = ( + )( + 3) = , luego + k ( + )( + )(( + ) + ) =. k= 6 Esto completa la demostració por iducció. (ii) Para el cálculo de I ( f ) y S ( f ) teemos que usar los putos x k = k co k = 0,,...,. La fució f (x) = x es creciete e [0,], así que podemos utilizar las fórmulas de la Observació..4: I ( f ) = f (x k ) = k= k= ( ) k = ( k k= ) = 3 S ( f ) = f (x k ) = k= k= Por otro lado, segú hemos visto e el apartado (i), se cumple k ( )( ) = k= 6 Sustituyedo e (.3) y (.4), obteemos y y k = k= I ( f ) = ( )( ) = ( ) k = 3 k= k (.3) k. (.4) k= ( + )( + ). 6 S ( f ) = ( + )( + ) = , como se quería demostrar. (iii) Por la defiició de itegral, x dx = lím S ( f ) = lím 6 = 6 = 3. 0 (iv) La fució cumple F (x) = x = f (x) para todo x R, así que F es primitiva de f e cualquier itervalo. Si aplicamos la Regla de Barrow (Teorema..3), obteemos el mismo resultado que e el apartado (iii): x dx = F() F(0) = = 3. 0
87 . Propiedades básicas y Regla de Barrow 8 Ejercicio..9. (i) Demuestra por iducció que = ( + ) 4 para todo N. (ii) Se cosidera la fució f (x) = x 3 e el itervalo [0,]. Co la ayuda de la fórmula del apartado (i), demuestra que para todo N. (iii) Calcula 0 I ( f ) = + 4 y S ( f ) = x 3 dx utilizado las fórmulas del apartado (ii). (iv) Comprueba que F(x) = x4 4 es ua primitiva de f (x) = x3 e [0,] y utilízala para calcular 0 x 3 dx mediate la Regla de Barrow. SOLUCIÓN. (i) Obviamete, la fórmula se cumple para =. Vamos a demostrar ahora que: k 3 = ( + ) k= 4 E efecto, basta observar que = + k= + k 3 = k 3 + ( + ) 3 = ( + ) + ( + ) 3 = k= k= 4 = ( + ) + 4( + ) 3 4 Esto completa la prueba por iducció. k 3 = ( + ) ( + ). 4 = ( + ) ( + 4( + )) 4 (ii) Para el cálculo de I ( f ) y S ( f ) usaremos los putos = ( + ) ( + ). 4 x k = k co k = 0,,...,. Como la fució f (x) = x 3 es creciete e [0,], podemos utilizar las fórmulas de la Observació..4 para obteer: I ( f ) = f (x k ) = k= k= ( k ) 3 = k= ( ) k 3 = 4 k= k 3 (.5)
88 8 Itegrales S ( f ) = f (x k ) = k= k= ( ) k 3 = 4 Por otro lado, segú hemos visto e el apartado (i), teemos k 3. (.6) k= k 3 = ( ) k= 4 Sustituyedo e (.5) y (.6), obteemos y k= k 3 = ( + ). 4 y como se quería demostrar. I ( f ) = 4 ( ) 4 S ( f ) = 4 ( + ) (iii) De la defiició de itegral se sigue que: 0 4 = + 4 = + + 4, x 3 dx = lím S ( f ) = lím = 4. (iv) F(x) = x4 4 cumple F (x) = x 3 = f (x) para todo x R, así que F es primitiva de f e cualquier itervalo. Si aplicamos la Regla de Barrow (Teorema..3) e el itervalo [0,], obteemos el resultado del apartado (iii): 0 x 3 dx = F() F(0) = = 4. Ejercicio..0. Calcula las itegrales siguietes aplicado la Regla de Barrow: π 0 sexdx π π cosxdx 0 e x dx e x dx SOLUCIÓN. La fució sex tiee primitiva cosx, luego π 0 sexdx = [ cosx ] ( π π ) 0 = cos ( cos0) = 0 + =.
89 . Propiedades básicas y Regla de Barrow 83 La fució cosx tiee primitiva sex, así que π π cosxdx = [ sex ] π = seπ se( π) = 0 0 = 0. π La fució e x tiee primitiva e x, luego 0 e x dx = [ e x] 0 = e e 0 = e. Fialmete, la fució x tiee primitiva lx, luego e x dx = [ lx ] e = le l = 0 =. Ejercicio... Calcula el área de la regió plaa limitada por las parábolas y = x, y = x y la recta y = x. SOLUCIÓN. Defiimos las fucioes f (x) = x, g(x) = x y h(x) = x. Los putos de corte de sus gráficas so x = 0, x = y x = 4 (véase la Figura.5). El área del recito señalado es A = x3 tiee primitiva. Aplicado la Regla de Barrow (Teore- 6 La fució f (x) g(x) = x ma..3) se obtiee 0 ( ) 4 ( ) f (x) g(x) dx + h(x) g(x) dx. 0 ( f (x) g(x) ) dx = [ x 3 6 ] 0 = 4 3. Por otro lado, la fució h(x) g(x) = x x tiee primitiva x x3. Usado otra vez 6 la Regla de Barrow teemos 4 Luego el área pedida es A = = 4. ( ) h(x) g(x) dx = [x x3 ] 4 6 = 8 3.
90 84 Itegrales Figura.5: Ejercicio... Ejercicio... Calcula el área de la regió plaa limitada la gráfica de la fució f (x) = x 3 x y su recta tagete e el puto de abscisas x =. SOLUCIÓN. La recta tagete pasa por el puto (, f ( )) = (,0). La derivada de la fució es f (x) = 3x, luego la pediete de la recta tagete vale f ( ) =. Por tato, la ecuació de dicha recta es y = x +. Las gráficas de las fucioes f (x) y g(x) = x + se corta e los putos cuyas abscisas so las solucioes de la ecuació: x 3 x = x + x 3 3x = 0 x {,}. E la Figura.6 podemos ver ua represetació gráfica de las fucioes f (x) y g(x). El área pedida es A = ( g(x) f (x) ) dx. La fució g(x) f (x) = x 3 + 3x + tiee primitiva x x + x. Usamos ahora la Regla de Barrow (Teorema..3) para calcular el área: [ A = x x ] + x = 7 4.
91 . Propiedades básicas y Regla de Barrow 85 Figura.6: Ejercicio... Ejercicio..3. Calcula el área del recito plao limitado por la parábola de ecuació y = 4x x y las rectas tagetes a la misma e los putos de corte co el eje OX. SOLUCIÓN. Las solucioes de la ecuació 4x x = 0 so x = 0 y x = 4. La derivada de la fució f (x) = 4x x es f (x) = 4 x. Calculamos las dos rectas tagetes: La tagete e el puto de abscisas x = 0 (cuyas coordeadas so (0, f (0)) = (0,0)) tiee pediete f (0) = 4. Luego la ecuació de dicha recta es y = 4x. La tagete e el puto de abscisas x = 4 (cuyas coordeadas so (4, f (4)) = (4,0)) tiee pediete f (4) = 4. Así que la ecuació de dicha recta es y = 4x + 6. La Figura.7 muestra ua represetació gráfica de la parábola y las dos rectas tagetes ateriores (que se corta e x = ). Si llamamos g(x) = 4x y h(x) = 4x + 6, el área del recito cosiderado es A = 0 ( ) 4 ( ) ( ) g(x) f (x) dx + h(x) f (x) dx = g(x) f (x) dx, dode la última igualdad es cosecuecia de la simetría que hay respecto de la recta x =. La fució g(x) f (x) = x tiee primitiva x3. Aplicado la Regla de Barrow 3 0
92 86 Itegrales (Teorema..3) obteemos el valor del área: [ x 3 ] A = 3 = = 6 3. Figura.7: Ejercicio..3. Ejercicio..4. Calcula los valores del parámetro a R para los que el área de la regió plaa limitada por la parábola y = 3x + 3a 4 y el eje OX es 56. SOLUCIÓN. Resolviedo la ecuació 3x +3a 4 = 0 vemos que la parábola corta al eje OX e los putos de abscisas x = a y x = a. Como la parábola es covexa, está por ecima del eje OX etre dichos putos. Así que el área de la regió plaa limitada por la parábola y el eje OX se calcula mediate la itegral siguiete: A(a) = a a ( 3x + 3a 4) dx. Ua primitiva de la fució 3x + 3a 4 es x 3 + 3a 4 x. Usado la Regla de Barrow (Teorema..3) teemos: A(a) = [ x 3 + 3a 4 x ] a a = 4a6.
93 . Propiedades básicas y Regla de Barrow 87 Fialmete, resolvemos la ecuació 56 = A(a) = 4a 6 64 = a 6, cuyas úicas solucioes so a = y a =.
94 88 Itegrales.. Cálculo de primitivas Coteidos Cambio de variable. Itegració por partes. Primitivas de fraccioes racioales. Teoría Para hallar la itegral de ua fució mediate la Regla de Barrow (Teorema..3) es ecesario ecotrar previamete ua primitiva de dicha fució. E geeral, el cálculo de primitivas es complicado y sólo es posible e casos particulares. E esta lecció estudiamos alguos métodos elemetales para calcular primitivas. Defiició... Si ua fució F(x) es primitiva de otra fució f (x) e algú itervalo, etoces escribimos: f (x)dx = F(x) +C. A la costate C (llamada costate de itegració ) se le puede asigar cualquier valor real. Para cada valor particular de C, la fució F(x)+C es ua primitiva de f (x). La siguiete tabla recoge alguas primitivas imediatas: PRIMITIVAS INMEDIATAS α dx = αx +C si α R dx = l x +C x α x dx = αx +C si α > 0 lα cosxdx = sex +C x s dx = xs+ +C si s s + e x dx = e x +C sexdx = cosx +C dx = arctax +C + x
95 . Cálculo de primitivas 89 Observació... (i) α f (x)dx = α f (x)dx si α R. ( ) (ii) f (x) + g(x) dx = f (x)dx + g(x) dx. La primera técica de cálculo de primitivas que vamos a estudiar es el cambio de variable (o método de sustitució): Proposició..3 (Fórmula del cambio de variable). Se cumple f (g(x))g (x)dx = F(g(x)) +C si F es ua primitiva de f. Demostració. Por la Regla de la Cadea, la derivada de la fució compuesta F(g(x)) es precisamete F (g(x))g (x) = f (g(x))g (x). Observació..4. E la práctica se suele defiir t = g(x) dt = g (x)dx y etoces el cambio de variable se escribe así: f (g(x))g (x)dx = f (t)dt = F(t) +C = F(g(x)) +C. Veamos alguos ejemplos cocretos dode se puede aplicar el método: Ejemplo..5. Calculamos las primitivas siguietes por cambio de variable: (i) e x dx (ii) xse(x )dx (iii) xlx dx Solució. (i) La fució e x puede escribirse como e x = f (g(x))g (x), siedo g(x) = x y f (t) = et. Ua primitiva de f (t) = et et es F(t) =. Aplicado la fórmula del cambio de variable obteemos e x dx = f (g(x))g (x)dx = F(g(x)) +C = ex +C.
96 90 Itegrales Habitualmete, cuado se calcula primitivas por cambio de variable, se procede del modo idicado e la Observació..4. E este ejemplo, eligiedo como ueva variable t = x, teemos dt = dx (derivamos x respecto de la variable x) y, sustituyedo e la primitiva a calcular, se obtiee e x dx = e t dt = e t dt. Esta última primitiva (respecto de la variable t) es imediata: e t dt = et +C. Fialmete, e esta última expresió sustituimos la variable t para que todo quede e fució de la variable x: e x dx = ex +C. (ii) Ahora elegimos como ueva variable t = x. Etoces dt = xdx (derivamos x respecto de la variable x) y, sustituyedo e la primitiva, os queda xse(x )dx = set dt = set dt. Esta última primitiva (respecto de la variable t) es imediata: set dt = cost +C. Fialmete, sustituimos la variable t para que todo quede e fució de la variable x: xse(x )dx = cos(x ) +C. (iii) Tomamos como ueva variable t = lx. Etoces dt = dx (derivamos lx x respecto de la variable x) y, sustituyedo, os queda xlx dx = t dt, que es ua primitiva imediata (respecto de la variable t): dt = l t +C. t
97 . Cálculo de primitivas 9 Sustituyedo la variable t, obteemos dx = l lx +C. xlx El segudo método de cálculo de primitivas que vamos a estudiar es el método de itegració por partes: Proposició..6 (Fórmula de itegració por partes). f (x)g (x)dx = f (x)g(x) f (x)g(x)dx Demostració. La derivada de la fució producto f (x)g(x) es f (x)g(x)+ f (x)g (x). Por tato: f (x)g(x)dx + Despejado, obteemos f (x)g (x)dx = ( f (x)g(x) + f (x)g (x) ) dx = f (x)g(x) +C. f (x)g (x)dx = f (x)g(x) Observació..7. E la práctica se suele escribir f (x)g(x)dx. u = f (x) dv = g (x)dx du = f (x)dx v = g(x) co lo que la fórmula de itegració por partes queda así: udv = uv vdu. A cotiuació vemos alguos ejemplos ilustrado el método. Ejemplo..8. Calculamos las primitivas siguietes mediate itegració por partes: (i) xcosxdx (ii) xe x dx (iii) x sexdx Solució. (i) Podemos escribir xcosx = f (x)g (x) eligiedo f (x) = x y g(x) = sex (ua primitiva de cosx). Aplicado la fórmula de itegració por partes: xcosxdx = f (x)g (x)dx = f (x)g(x) f (x)g(x)dx = xsex sexdx.
98 9 Itegrales Esta última primitiva es imediata: sexdx = cosx +C. Por tato: xcosxdx = xsex + cosx +C. [E este ejemplo, hemos elegido u = x y dv = cosxdx, co lo que du = dx (derivamos x) y v = sex (escogemos ua primitiva de cosx).] (ii) Podemos escribir xe x dx = udv eligiedo u = x y dv = e x dx. Etoces du = dx (derivamos x) y v = e x (primitiva de e x ). Aplicado la fórmula de itegracio por partes, obteemos xe x dx = udv = uv Como e x dx = e x +C, deducimos que vdu = xe x xe x dx = xe x e x +C = e x (x ) +C. (iii) Escribimos x sexdx = udv eligiedo u = x y dv = sexdx. e x dx. Etoces du = xdx (derivamos x ) y v = cosx (primitiva de sex). Aplicado la fórmula de itegracio por partes, obteemos x sexdx = udv = uv vdu = = x cosx x( cosx)dx = x cosx + Segú hemos visto e el apartado (i), esta última primitiva es xcosxdx = xsex + cosx +C, xcosxdx. luego x sexdx = x cosx + ( xsex + cosx ) +C = ( x )cosx + xsex +C.
99 . Cálculo de primitivas 93 Fializamos la lecció explicado cómo se puede calcular primitivas de fraccioes racioales secillas. Lo vemos sobre alguos ejemplos cocretos. Recordamos que ua fracció racioal es el cociete de dos poliomios. Por ejemplo: 0x 6 5x 4 + 3x 3 x + x 0 7x 4 + x 3 + x 0x + 7 x (x + )(x + ) E geeral, para poder calcular la primitiva de ua fracció racioal P(x) es ecesario que Q(x) el grado del umerador P(x) sea estrictamete meor que el grado del deomiador Q(x). Si o es así, podemos realizar la divisió de ambos poliomios y escribir P(x) R(x) = C(x) + Q(x) Q(x), dode C(x) es el cociete y R(x) es el resto de dicha divisió. Ejemplo..9. Calculamos las primitivas siguietes: (i) x 4 dx (ii) x x (x ) dx (iii) + 3 x(x ) dx Solució. (i) El deomiador se descompoe como producto de dos factores lieales distitos: x 4 = (x )(x + ). Por tato, la fracció racioal se puede escribir como suma de dos fraccioes simples: x 4 = A x + B x + para ciertas costates A,B R. Para calcularlas, operamos x 4 = A x + B A(x + ) + B(x ) = x + x 4 etc. (.7) e igualamos umeradores: = A(x+)+B(x ). Sustituyedo e esta idetidad x = y x = obteemos las ecuacioes = 4B y = 4A, luego A = 4 y B = 4. Sustituyedo estos valores e (.7) y tomado primitivas deducimos: ( x 4 dx = 4 x 4 ) dx = x + = 4 x dx 4 x + dx = 4 l x l x + +C. 4
100 94 Itegrales (ii) E este caso, el deomiador es el cuadrado de u factor lieal y, por tato, la fracció racioal se puede escribir como suma de dos fraccioes simples de la forma siguiete: x (x ) = A x + B (x ) (.8) para ciertas costates A,B R. Para calcularlas, operamos x (x ) = A x + B A(x ) + B = (x ) (x ) e igualamos umeradores: x = A(x ) + B. E esta idetidad podemos sustituir x = y x = 0 obteiedo = B y 0 = A + B, de dode deducimos que A =. Reemplazado estos valores y tomado primitivas e (.8) resulta que x ( (x ) dx = x + ) (x ) dx = = x dx + dx = l x (x ) x +C. (iii) El deomiador es el producto de u factor lieal (x) y el cuadrado de otro factor lieal distito (x ). E esta situació, podemos escribir la fracció racioal como suma de tres fraccioes simples, de la maera siguiete: x + 3 x(x ) = A x + B x + D (x ) (.9) para ciertas costates A,B,D R que vamos a determiar. Para ello, operamos e igualamos umeradores: x + 3 x(x ) = A x + B x + D (x ) = A(x ) + Bx(x ) + Dx x(x ), luego x + 3 = A(x ) + Bx(x ) + Dx. E esta idetidad sustituimos x por tres valores distitos: x = = 5 = D. x = 0 = 3 = A. x = = = A + B + D, de dode obteemos B =.
101 . Cálculo de primitivas 95 Fialmete, sustituimos estos valores e (.9) y tomamos primitivas: x + 3 ( 3 x(x ) dx = x x + 5 ) (x ) dx = = 3 x dx x dx dx = 3l x l x (x ) x +C. Ejemplo..0. Calculamos las primitivas siguietes: (i) x + x + 3 dx (ii) x x + x + 3 dx Solució. (iii) x(x + x + ) dx (i) El deomiador es u poliomio de grado si raíces reales. Como el umerador es ua costate, vamos a relacioar la primitiva co ua que ya coocemos: t dt = arcta(t) +C. + Operamos x + x + 3 = (x + ) + = ( ) x+ + y tomamos primitivas, obteiedo x + x + 3 dx = ( ) dx. x+ + E esta última primitiva realizamos el cambio de variable t = x +. Etoces dt = dx y al sustituir os queda: x + x + 3 dx = t + dt = arcta(t) +C = ( x + ) arcta +C. (ii) El deomiador es el mismo que e el apartado (i), pero e esta ocasió el umerador o es costate. Realizamos la siguiete trasformació para hacer aparecer la derivada del deomiador e el umerador: x x + x + 3 = x x + x + 3 = ( x + x + x + 3 ) x. + x + 3
102 96 Itegrales Tomado primitivas os queda: x x + x + 3 dx = x + x + x + 3 dx x + x + 3 dx. La primera primitiva se resuelve de forma imediata (aplicado el cambio de variable t = x + x + 3), mietras que la seguda es la que hemos calculado e el apartado (i). Así, teemos x x + x + 3 dx = l x + x + 3 ( x + ) arcta +C. (iii) El deomiador es el producto de ua factor lieal (x) y u poliomio de grado si raíces reales (x + x + ). E esta situació, la fracció racioal se puede escribir de la siguiete maera: x(x + x + ) = A x + Bx + D x + x + para ciertas costates A,B,D R a determiar. Para ello, operamos x(x + x + ) = A x + Bx + D x + x + = A(x + x + ) + (Bx + D)x x(x + x + ) (.0) e igualamos umeradores: = A(x +x+)+(bx+d)x. Sustituimos tres valores de x e la idetidad aterior: x = 0 = = A. x = = = 3A + B + D = B + D =. x = = = A + B D = B = D. Por tato, A =, B = D =. Sustituyedo e (.0) y tomado primitivas, os queda x(x + x + ) dx = x dx x + x dx. (.) + x + La primera de estas primitivas es imediata, mietras que la seguda se puede resolver por el método del apartado (ii). E efecto: x + x + x + dx = x + x + x + dx = = x + x + x + dx + x + x + dx = l x + x + + x dx. (.) + x +
103 . Cálculo de primitivas 97 Por otro lado, x + x + dx = ( ) x + dx = ( ) dx = ( x + ) arcta +C, x dode e el último paso hemos realizado el cambio de variable t = x + 3. Fialmete, sustituimos e (.) y (.): x(x + x + ) dx = l x l x + x + ( x + ) arcta +C. 3 3 Como ya hemos cometado, calcular primitivas puede ser ua tarea muy difícil. Icluso hay primitivas que o se puede expresar e térmios de fucioes elemetales mediate ua fórmula secilla, por ejemplo: sex e x dx dx cos(x )dx etc. x E ciecias experimetales e igeiería, las itegrales se suele calcular de forma aproximada mediate métodos uméricos, como veremos e la Lecció.4. Ejercicios Ejercicio... Ecuetra ua fució f (x) que cumpla las siguietes tres propiedades: (a) f (x) = (x + ) 3 (b) f (0) = 0 (c) f (0) = 0 SOLUCIÓN. E primer lugar, calculamos la primitiva de la fució (x + ) 3 realizado el cambio de variable t = x +. Etoces dt = dx (derivamos x + respecto de la variable x) y al sustituir queda: (x + ) 3 dx = Por tato, la fució buscada debe cumplir t 3 dt = t +C = (x + ) +C. f (x) = (x + ) +C
104 98 Itegrales para ua cotate C apropiada. Debe cumplirse lo siguiete: 0 = f (0) = +C, luego C =. Por tato, f (x) = (x + ) +. A cotiuació calculamos la primitiva de la fució realizado el mismo cambio de variable t = x + : (x + ) Luego f (x) = (x + ) dx = t dt = t + D = (x + ) + D. (x + ) + x + D para ua cierta costate D, que debe cumplir 0 = f (0) = + D. Por tato, la fució pedida es f (x) = (x + ) + x. Ejercicio... Calcula las primitivas siguietes por cambio de variable: (i) se 5 xcosxdx (ii) x 3 + x 4 dx (iii) e x + e x dx (iv) x 3 e x4 + dx SOLUCIÓN. (i) Hacemos el cambio de variable t = sex. Etoces dt = cosxdx (derivamos sex respecto de la variable x) y, sustituyedo, os queda se 5 xcosxdx = t 5 dt = t6 6 +C = se6 x 6 +C. (ii) Tomamos como ueva variable t = + x 4. Etoces dt = 4x 3 dx (derivamos + x 4 respecto de la variable x) y, sustituyedo, obteemos x 3 dx = dt = + x 4 4 t t dt = t +C = + x 4 +C. (iii) Hacemos el cambio de variable t = e x, luego dt = e x dx. Sustituyedo: e x + e x dx = e x + (e x ) dx = +t dt = arctat +C = arcta(ex ) +C.
105 . Cálculo de primitivas 99 (iv) Tomamos t = x 4 +, luego dt = 8x 3 dx. Etoces: x 3 e x4 + dx = 8 et dt = 8 e t dt = et ex4+ +C = +C. 8 8 Ejercicio..3. Calcula las primitivas siguietes por cambio de variable: x 3x (i) ( + x ) 4 dx (ii) + dx (iii) x cos(x 3 + )dx (iv) sexcos 3 xdx SOLUCIÓN. (i) Haciedo el cambio de variable t = + x, os queda dt = xdx y al sustituir obteemos: x ( + x ) 4 dx = t 4 dt = 6t 3 +C = 6( + x ) 3 +C. (ii) Tomamos t = 3x +, de maera que dt = 3dx y así 3x t + dx = 3 dt = t t 3/ (3x + )3/ dt = +C = +C (iii) Eligiedo la ueva variable t = x 3 +, teemos dt = 3x dx y etoces x cos(x 3 + )dx = cost 3 dt = 3 cost dt = set 3 +C = se(x3 + ) +C. 3 (iv) Hacemos el cambio t = cosx, que da dt = sexdx y al sustituir os queda: sexcos 3 xdx = t 3 dt = t4 4 +C = cos4 x 4 +C. Ejercicio..4. Calcula las primitivas siguietes mediate el método de itegració por partes: (i) lxdx (ii) xlxdx (iii) x e x dx (iv) e x sexdx
106 00 Itegrales SOLUCIÓN. (i) Podemos escribir lxdx = udv eligiedo u = lx y dv = dx. Etoces du = dx (derivamos lx) y v = x (primitiva de la fució costate ). Aplicado la fórmula de itegració por partes, x obteemos lxdx = udv = uv vdu = = xlx x x dx = xlx dx = xlx x +C = x(lx ) +C. (ii) Ahora escribimos xlxdx = udv eligiedo u = lx y dv = xdx. Etoces du = x dx (derivamos lx) y v = (primitiva de x). Aplicamos la fórmula de x itegració por partes: xlxdx = udv = uv vdu = = x x lx x dx = x lx xdx = x (iii) Comezamos escribiedo x e x dx = lx x 4 u = x y dv = e x dx. +C = x udv co la elecció: ( lx ) +C. Etoces du = xdx (derivamos x ) y v = e x (primitiva de e x ). Aplicamos la fórmula de itegració por partes: x e x dx = udv = uv vdu = = x e x e x xdx = x e x xe x dx. Segú el Ejemplo..8 (ii), xe x dx = e x (x )+C (se obtiee mediate itegració por partes), luego x e x dx = x e x e x (x ) +C = e x (x x + ) +C.
107 . Cálculo de primitivas 0 (iv) Escribimos e x sexdx = udv eligiedo u = sex y dv = e x dx. Etoces du = cosxdx (derivamos sex) y v = e x (primitiva de e x ). Por tato: e x sexdx = udv = uv vdu = e x sex e x cosxdx. (.3) Aparece así la primitiva e x cosxdx, a la que vamos a aplicar la fórmula de itegració por partes tomado u = cosx y dv = e x dx, de maera que du = sexdx y v = e x. Etoces e x cosxdx = udv = uv vdu = = e x cosx e x ( sex)dx = e x cosx + e x sexdx. Sustituyedo esta expresió de e x cosxdx e (.3), obteemos ( e x sexdx = e x sex e x cosx + ) e x sexdx = e x (sex cosx) de dode podemos despejar: e x sexdx = ex (sex cosx) +C. e x sexdx, Ejercicio..5. Calcula las primitivas siguietes mediate itegració por partes: (i) xe x dx (ii) x 3 cos(x )dx (iii) e x cos(3x)dx (iv) x(x + ) 0 dx SOLUCIÓN. (i) Aplicado el cambio de variable t = x, teemos dt = dx y al sustituir obteemos xe x dx = te t dt. Esta última primitiva ya la hemos calculado e el apartado (ii) del Ejemplo..8: te t dt = (t )e t +C.
108 0 Itegrales Por tato: xe x dx = (t )e t +C = (x + )e x +C. Alterativamete, se puede calcular esta primitiva de maera directa mediate itegració por partes, eligiedo u = x y dv = e x dx. (ii) Escribimos x 3 cos(x )dx = udv eligiedo u = x y dv = xcos(x )dx. Etoces du = xdx (derivamos x ) y v = se(x ) (primitiva de la fució xcos(x )). Aplicamos ahora la fórmula de itegració por partes: x 3 cos(x )dx = udv = uv vdu = = x se(x ) xse(x )dx = x se(x ) + cos(x ) +C = x se(x ) + cos(x ) +C. (iii) Podemos escribir e x cos(3x)dx = udv tomado u = e x y dv = cos(3x)dx. Etoces du = e x dx (derivamos e x ) y v = 3 se(3x) (primitiva de la fució cos(3x)). Aplicado la fórmula de itegració por partes, obteemos: e x cos(3x)dx = udv = uv vdu = ex se(3x) e x se(3x)dx. (.4) 3 3 E esta última primitiva volvemos a aplicar itegració por partes eligiedo u = e x y dv = se(3x)dx, de maera que du = e x dx y v = 3 cos(3x), luego e x se(3x)dx = udv = uv Sustituyedo e (.4) deducimos: e x cos(3x)dx = ex se(3x) 3 = ex se(3x) ( ex cos(3x) 3 = ex 3 vdu = ex cos(3x) e x cos(3x)dx. e x se(3x)dx = + ) e x cos(3x)dx = 3 (se(3x) + 3 ) cos(3x) 4 e x cos(3x)dx. 9
109 . Cálculo de primitivas 03 De aquí podemos despejar e x cos(3x)dx obteiedo e x cos(3x)dx = (se(3x) 3ex + 3 ) 3 cos(3x) +C. (iv) E este caso escribimos x(x + ) 0 dx = udv eligiedo u = x y dv = (x + ) 0 dx. (x + ) Etoces du = dx, v = y la fórmula de itegració por partes os da x(x + ) 0 dx = udv = uv vdu = = x(x + ) (x+) dx = x(x + ) (x + ) 3 +C = (x + ) (x ) +C. 3 Ejercicio..6. Calcula las siguietes primitivas: l(3x) (i) x sexdx (ii) x dx (iii) x (x + ) dx (iv) 5 x se(x + )dx SOLUCIÓN. (i) Si aplicamos el método de itegració por partes eligiedo u = x y dv = sexdx, teemos du = l x dx, v = cosx y os queda: x sexdx = udv = uv vdu = x cosx + l x cosxdx. (.5) A esta última primitiva le podemos aplicar de uevo el método de itegració por partes eligiedo u = x y dv = cosxdx, de maera que du = l x dx, v = sex y así: x cosxdx = udv = uv vdu = x sex l x sexdx. (.6) Llamado I = x sexdx y sustituyedo (.6) e (.5), obteemos la ecuació: I = x cosx + l ( x sex l I). Despejado I e esta ecuació, deducimos que x sexdx = x (l sex cosx) + (l) +C.
110 04 Itegrales (ii) Ahora aplicamos el método de itegració por partes co la elecció u = l(3x) y dv = x dx, de maera que du = x dx, v = x y así: l(3x) x dx = l(3x) x + dx = l(3x) x x x = l(3x) + +C. x (iii) Vamos a utilizar la fórmula de itegració por partes eligiedo u = (x + ) y dv = x dx. Etoces du = (x + )dx, v = x y os queda: l x (x + ) dx = udv = uv vdu = x (x + ) l + l x (x + )dx. A esta última primitiva tambié le podemos aplicar el método de itegració por partes tomado u = x + y dv = x dx, de maera que du = dx, v = x l y así: Por tato: x (x + )dx = x (x + ) l x (x + ) dx = x (x + ) l + l + ( l = x l x dx = x (x + ) l ) x (l) +C = x (l) +C. x (x + ) l ( (x + ) + (x + ) + l (l) (iv) Podemos escribir 5 x se(x + )dx = udv eligiedo u = 5 x y dv = se(x + )dx. ) +C Etoces du = l5 5 x dx, v = cos(x + ) y la fórmula de itegració por partes os da 5 x se(x + )dx = 5 x cos(x + ) + l5 5 x cos(x + )dx. (.7) A esta primitiva le podemos aplicar de uevo el método de itegració por partes tomado u = 5 x y dv = cos(x + )dx, de maera que du = l5 5 x dx, v = se(x + ) y así: 5 x cos(x + )dx = 5 x se(x + ) l5 5 x se(x + )dx. (.8)
111 . Cálculo de primitivas 05 Llamado I = 5 x se(x + )dx y sustituyedo (.8) e (.7), obteemos la ecuació: I = 5 x cos(x + ) + l5 (5 x se(x + ) l5 I). Fialmete, despejado I e esta ecuació, deducimos: 5 x se(x + )dx = 5x (l5 se(x + ) cos(x + )) + (l5) +C. Ejercicio..7. Calcula las siguietes itegrales: 0 ( (i) ta x + π ) π dx (ii) 4 π 4 π se 3( x ) ( x cos dx ) (iii) 3π π sex e cosx dx (iv) 0 8 x 3 + x 8 dx SOLUCIÓN. E cada apartado, vamos a calcular primero ua primitiva de la fucio a itegrar, para aplicar después la Regla de Barrow (Teorema..3). (i) Buscamos la primitiva mediate el cambio de variable t = cos ( x + π 4 ), de maera que dt = se ( x + π ) 4 dx y así: ( ta x + π ) ( ) se x + π dx = 4 ( 4 cos ( x + π ) cos dx = t dt = l t +C = l x + π ) +C. 4 4 Ahora calculamos la itegral mediate la Regla de Barrow: 0 ( ta x + π ) [ ( dx = l cos x + π ) ] 0 ( π ) l = l cos + l cos0 = π 4 (ii) Para la primitiva usamos el cambio de variable t = se ( x ), así dt = cos ( x ) dx y etoces se 3( x ) ( x cos dx = ) π 4 ( x t 3 dt = t4 se 4 +C = ) +C. Ahora calculamos la itegral co la Regla de Barrow: ( x ) π ( π se 3( x ) ( x cos dx = ) se4 se 4 π ) ( se 4 π ) = 4 4 = 0, π π
112 06 Itegrales ya que se( π 4 ) = se( π 4 ). (iii) Primero hallamos la primitiva mediate el cambio de variable t = cosx, de maera que dt = sexdx y os queda: sex e cosx dx = e t dt = e t dt = e t Calculamos la itegral mediate la Regla de Barrow: 3π π [ sex e cosx ] 3π dx = ecosx π = e cos( 3π ) +C = e cosx e cos(π) +C. = e. (iv) Para hallar la primitiva tomamos como ueva variable t = x4, así dt = 4x3 dx y además t = x 8. Sustituyedo: x 3 + x 8 dx = 4 + t dt = 8 Calculamos ahora la itegral pedida co la Regla de Barrow: [ 0 x 3 ( x 4 ) ] 0 + x 8 dx = 8 arcta = 8 ( x 4 +t dt = arctat +C = 8 8 arcta )+C. 8 8 arcta0 π 8 arcta = 3. Ejercicio..8. Calcula las siguietes itegrales: SOLUCIÓN. (iii) 0 (i) e 3 x x dx 3 l(3x) x (iv) dx (ii) x lxdx 0 x x + e (v) x(lx) dx E cada apartado, vamos a calcular primero ua primitiva de la fucio a itegrar, para aplicar después la Regla de Barrow (Teorema..3). l(3x) (i) Calculamos la primitiva dx mediate el cambio de variable t = l(3x). x Etoces dt = 3 3x dx = dx y, sustituyedo, teemos: x l(3x) dx = t dt = t (l(3x)) +C = +C. x
113 . Cálculo de primitivas 07 Aplicamos ahora la Regla de Barrow para calcular la itegral pedida: e [ 3 l(3x) (l(3x)) ] e 3 dx = 3 x (ii) Calculamos la primitiva Etoces dt = xdx y así x x + dx = t dt = = (le) (l) = 0 =. 3 x x + dx mediate el cambio de variable t = x +. t t 3 dt = +C = t 3 3 Utilizamos la Regla de Barrow para calcular la itegral pedida: x x + dx = [ (x + ) 3 ] = ( + ) C = (x + ) 3 (0 + ) =. 3 +C (iii) Vamos a calcular la primitiva x x dx mediate itegració por partes, eligiedo u = x y dv = x dx. Etoces du = dx y v = x l (primitiva de x ), luego x x dx = udv = uv vdu = = xx l x xx dx = l l l x dx = xx l ( x x +C = x ) +C. (l) l l Aplicamos la Regla de Barrow: [ x x x ( dx = x )] ( = ) ( 0 0 ) = 8 0 l l 0 l l l l l 3 (l). (iv) Calculamos la primitiva x lxdx mediate itegració por partes, eligiedo Etoces du = x3 dx, v = x 3 dx y x lxdx = udv = uv vdu = = x3 lx 3 x 3 3 x dx = x3 lx 3 3 u = lx y dv = x dx. x dx = x3 lx 3 x3 9 +C = x3 3 ( lx ) +C. 3
114 08 Itegrales Fialmete, para calcular la itegral pedida, utilizamos la Regla de Barrow: [ x x 3 lxdx = 3 = 3 3 ( lx )] 3 ( l 3 = ) 3 3 ( l ) = 8 ( l ) = 8l (v) E primer lugar, calculamos la primitiva aplicado el método de itegració por partes eligiedo u = (lx) y dv = xdx. Etoces du = lx dx y v = x. Por tato: x x(lx) dx = udv = uv vdu = = x (lx) x lx dx = x (lx) x xlxdx. Y esta última primitiva tambié se calcula mediate itegració por partes (véase el apartado (ii) del Ejercicio..4): Sustituyedo, obteemos: x(lx) dx = x (lx) xlxdx = x x ( lx ) +C. ( lx ) ( +C = x (lx) lx + ) +C. Ahora podemos aplicar la Regla de Barrow para calcular la itegral pedida: e [ x x(lx) dx = = e ya que le = y l = 0. ( (lx) lx + )] e ( (le) le + = ) ( (l) l + ) = ( e ), 4 Ejercicio..9. Calcula las siguietes primitivas: (i) x 3 x dx (ii) + x + x(x ) dx (iii) x(x + ) dx
115 . Cálculo de primitivas 09 SOLUCIÓN. (i) El deomiador se descompoe como producto de dos factores lieales distitos: x = (x )(x + ). Por tato, podemos escribir la fracció racioal como suma de dos fraccioes simples del modo siguiete: x = A x + B x + para ciertas costates A,B R a determiar. Operado x = A x + B A(x + ) + B(x ) = x + x e igualado umeradores, teemos: = A(x + ) + B(x ). Sustituyedo e esta idetidad x = y x = obteemos = B y = A, luego A = y B =. Por tato: x dx = ( x = ) x + x dx dx = x + dx = l x l x + +C. (ii) E la fracció racioal dada, el umerador y el deomiador tiee el mismo grado. Así que e primer lugar debemos realizar la divisió de x 3 + x + etre x(x ), que da como cociete y como resto x +. Por tato: x 3 + x + x(x ) = + x + x(x ). (.9) x + Teemos que calcular la primitiva de la fracció racioal x(x, cuyo deomiador es ) el producto de tres factores lieales distitos: x, x y x +. E esta situació, podemos escribir la fracció racioal como suma de tres fraccioes simples: x + x(x ) = A x + B x + D x + para ciertas costates A,B,D R a determiar. Para ello, operamos e igualamos umeradores: x + x(x ) = A x + B x + D x + A(x )(x + ) + Bx(x + ) + Dx(x ) = x(x, ) luego x + = A(x )(x + ) + Bx(x + ) + Dx(x ). Damos valores a x:
116 0 Itegrales x = 0 = A =. x = = B = 3. x = = D =. Sustituimos y tomamos primitivas: x + ( x(x ) dx = x + 3 (x ) (x + ) = x dx + 3 x dx ) dx = x + dx = l x + 3 l x l x + +C. Fialmete, teiedo e cueta (.9) obteemos la primitiva buscada: x 3 + x + x(x ) dx = x + x + x(x ) dx = x l x + 3 l x l x + +C. (iii) El deomiador es el producto de u factor lieal (x) y el cuadrado de otro factor lieal distito (x + ). Etoces podemos escribir la fracció racioal como suma de tres fraccioes simples: x(x + ) = A x + B x + + D (x + ) para ciertas costates A,B,D R que vamos a determiar. Operamos x(x + ) = A x + B x + + D (x + ) = A(x + ) + Bx(x + ) + Dx x(x + ) e igualamos umeradores: = A(x + ) + Bx(x + ) + Dx. E esta idetidad sustituimos x por tres valores: x = 0 = A =. x = = D =. x = = = 4A + B + D, de dode B =. Para termiar, sustituimos y tomamos primitivas: ( x(x + ) dx = x x + ) (x + ) dx = l x l x + + x + +C. Ejercicio..0. Calcula las siguietes primitivas: (i) 4x 4x + 5 dx (ii) x x + x + 0 dx
117 . Cálculo de primitivas SOLUCIÓN. (i) El deomiador de la fracció racioal dada es u poliomio de grado si raíces reales. Teemos: 4x 4x + 5 = 4 x x = 4 ( x ) +, luego 4x 4x + 5 dx = 4 ( ) x dx = ( + 4 arcta x ) +C, dode la última primitiva la hemos resuelto mediate el cambio de variable t = x. (ii) El deomiador de la fracció racioal es de uevo u poliomio de grado si raíces reales. A diferecia del apartado (i), e este caso el umerador o es costate y operamos de la maera siguiete: luego x x + x + 0 dx = x x + x + 0 = x + x + x + 0 x + x + 0, x + x + x + 0 dx x + x + 0 dx = = l(x + x + 0) x + x + 0 dx. Esta última primitiva la calculamos mediate el procedimieto del apartado (i): x + x + 0 dx = (x + ) + 9 dx = 9 ( x+ 3 Realizamos el cambio de variable t = x + (dt = dx) y queda: 3 3 x + x + 0 dx = 9 Por tato: ) dx. + 3 t + dx = 3 arcta(t) +C = ( x + 3 arcta 3 x x + x + 0 dx = l(x + x + 0) ( x + ) 3 arcta +C. 3 ) +C.
118 Itegrales.3. Itegrales impropias Coteidos Itegrales impropias e itervalos o acotados. Criterios de Comparació. Teoría E esta lecció estudiamos las itegrales impropias de fucioes cotiuas defiidas e itervalos cerrados pero o acotados. Defiició.3.. Sea f : [a,) R ua fució cotiua. Para cada b > a podemos cosiderar la itegral etoces escribimos b y decimos que la itegral impropia dicha itegral impropia diverge. a f (x)dx. Si existe el límite b lím f (x)dx = L R b a a a f (x)dx = L f (x) dx coverge. E caso cotrario, decimos que Si f (x) 0 para todo x a y la itegral impropia a f (x)dx coverge, etoces el valor de dicha itegral impropia es el área del recito compredido etre la gráfica de f, el eje OX y la recta x = a.
119 .3 Itegrales impropias 3 Observació.3.. Sea f : [a, ) R ua fució cotiua y c > a. Etoces: E tal caso, a a f (x)dx = f (x) dx coverge c a f (x)dx + f (x)dx. c c f (x) dx coverge. Demostració. Basta observar que para cualquier b > c se cumple b c b f (x)dx = f (x)dx + f (x)dx, a a c segú la Proposició... Veamos u primer ejemplo de itegral impropia covergete: Ejemplo.3.3. La itegral impropia Demostració. Vamos a calcular la itegral 0 e x dx coverge y vale. b 0 e x dx para b > 0, buscado primero ua primitiva de la fució e x y aplicado después la Regla de Barrow (Teorema..3). Co el cambio de variable t = x teemos dt = dx y e x dx = e t dt = e t dt = e t +C = e x +C, así que b Como lím b e b = 0, obteemos 0 Por tato, la itegral impropia coverge y e x dx = [ e x] b 0 = e b ( e 0 ) = e b. b lím e x dx = lím ( e b ) = 0 =. b 0 b El siguiete ejemplo será útil más adelate. Ejemplo.3.4. La itegral impropia coverge para p > y diverge para p. 0 e x dx =. x p dx
120 4 Itegrales b Demostració. Calculamos primero la itegral x p dx para b > 0. La primitiva es imediata: x p+ x p dx = x p +C si p, dx = p + l x +C si p =. Aplicado la Regla de Barrow (Teorema..3), deducimos: x p dx b [ x p+ ] b x p dx = = b p+ p + p + p+ p + = b p+ p + b x dx = [ lx ] b = lb l = lb. Distiguimos ahora los dos casos. p Teiedo e cueta que lím x xc = 0 si c < 0 si c > 0 si p, cocluimos que b b p+ lím dx = lím b xp b p + = si p >, p + si p <. Por tato, la itegral impropia p = La itegral impropia Esto completa la demostració. dx coverge para p > y diverge para p <. xp dx diverge, ya que x b lím dx = lím lb =. b x b A veces, estudiar la covergecia de ua itegral impropia directamete (es decir, usado ua primitiva) puede ser complicado o icluso imposible, como ocurre co la fució e x (véase el Ejemplo.3.6 de abajo). E tales casos, se ecesita métodos idirectos, como los que presetamos e las dos proposicioes siguietes.
121 .3 Itegrales impropias 5 Proposició.3.5 (Criterio de Comparació I). Sea f,g : [a,) R dos fucioes cotiuas tales que 0 f (x) g(x) para todo x a. Se cumple: (i) Si (ii) Si a a g(x)dx coverge, etoces f (x)dx diverge, etoces Ejemplo.3.6. La itegral impropia a a 0 f (x)dx tambié coverge. g(x)dx tambié diverge. e x dx es covergete. Utilizado matemáticas π. más avazadas se puede demostrar que dicha itegral impropia vale Demostració. Segú la Observació.3., basta demostrar que la itegral impropia e x dx coverge. Para ello, vamos a aplicar el Criterio de Comparació I a las fucioes f (x) = e x y g(x) = e x. E primer lugar, veamos que 0 < e x e x para todo x. (.0) E efecto, la desigualdad 0 < e x se cumple porque e t > 0 para todo t R. Por otro lado, teemos x I = x x = x x II = e x e x, dode I = es cosecuecia de multiplicar por x la desigualdad x, mietras que = II se deduce del hecho de que la fució e t es creciete. Por otro lado, la itegral impropia e x dx coverge (véase el Ejemplo.3.3 y la Observació.3.). E vista de (.0), podemos aplicar el Criterio de Comparació I (Proposició.3.5) para deducir que la itegral impropia como se quería demostrar. e x dx tambié coverge, Proposició.3.7 (Criterio de Comparació II). Sea f,g : [a,) R dos fucioes cotiuas o egativas tales que existe: Se cumple: (i) Si C = 0 y a f (x) C = lím x g(x) R {}. g(x)dx coverge, etoces a f (x)dx tambié coverge.
122 6 Itegrales (ii) Si C = y a f (x)dx coverge, etoces (iii) Si C (0, ) etoces f (x) dx coverge Ejemplo.3.8. La itegral impropia x x 4 dx es covergete, mietras que la ite- + gral impropia a x x + x + dx es divergete. a Demostració. Segú hemos visto e el Ejemplo.3.4, lím x a g(x)dx tambié coverge. g(x)dx coverge. x x 4 + x 3 =, dx coverge. Como x3 x el Criterio de Comparació II garatiza que x 4 dx coverge. Por otro lado, la + itegral impropia dx diverge (Ejemplo.3.4). Como x lím x el Criterio de Comparació II os dice que x x + x + x =, x x dx diverge. + x + Fializamos la lecció itroduciedo el cocepto de itegral impropia para fucioes defiidas e todo R o e itervalos de la forma (,b]. Defiició.3.9. Sea f : (, b] R ua fució cotiua. Para cada a < b podemos cosiderar la itegral b a f (x)dx. Si existe el límite etoces escribimos b lím f (x)dx = L R a a b f (x)dx = L
123 .3 Itegrales impropias 7 y decimos que la itegral impropia dicha itegral impropia diverge. b f (x) dx coverge. E caso cotrario, decimos que Defiició.3.0. Sea f : R R ua fució cotiua. Decimos que la itegral impropia f (x) dx coverge si las itegrales impropias tal caso, escribimos f (x)dx = 0 0 f (x)dx + E caso cotrario, decimos que la itegral impropia Ejemplo.3.. La itegral impropia f (x)dx y 0 0 f (x)dx. f (x) dx diverge. dx coverge y vale π. + x Demostració. Vamos a comezar estudiado la itegral impropia ayuda de la primitiva (imediata) dx = arctax +C. + x f (x)dx coverge. E Dado a < 0, podemos aplicar la Regla de Barrow (Teorema..3) obteiedo 0 a 0 + x dx = [ arctax ] 0 = arcta0 arctaa = arctaa. a Como lím arctax = π, deducimos que x 0 lím a a 0 luego la itegral impropia ( ) π dx = lím + x arctaa = a, + x dx coverge y vale π. De maera similar, se puede comprobar que la itegral impropia dx co- + x verge y vale π. Por tato, la itegral impropia + x dx = 0 dx coverge y + x + x dx + + x dx = π + π = π. 0 0 dx co la + x
124 8 Itegrales Ejercicios Ejercicio.3.. Determia si las siguietes itegrales impropias coverge y, e tal caso, calcula su valor: (i) x + dx (ii) 0 xe x dx (iii) SOLUCIÓN. (i) Comezamos calculado ua primitiva de e x(lx) dx (iv) 0 de variable t = x +, de maera que dt = dx y así: dx = t / dt = t +C = x + +C. x + Ahora aplicamos la Regla de Barrow (Teorema..3) para calcular fució de b > : b x + x dx x + mediate el cambio x + dx = [ x + ] b = b + + = ( b + 3 ). Fialmete, como lím x x =, obteemos b lím dx = lím ( b + 3 ) =, b x + b b x + dx e luego la itegral impropia dx diverge. x + (ii) Calculamos la primitiva xe x dx mediate itegració por partes, tomado u = x y dv = e x dx. Etoces du = dx y v = e x. Aplicado la fórmula de itegració por partes, obteemos xe x dx = xe x e x dx = xe x e x +C = e x (x + ) +C. Ahora utilizamos la Regla de Barrow (Teorema..3) para calcular la itegral de la fució xe x e el itervalo [0,b], siedo b > 0 arbitrario: b 0 xe x dx = [ e x (x+) ] b 0 = e b (b+)+e 0 (0+) = e b (b+)+ = b + e b +.
125 .3 Itegrales impropias 9 b + Como lím b e b = 0 (por la Regla de L Hôpital, Teorema.3.6), deducimos: b lím xe x dx = lím b 0 b Por tato, la itegral impropia ( b + 0 ) e b + xe x dx coverge y vale. (iii) E primer lugar, hallamos la primitiva de = lím b b + e b + = 0 + =. mediate el cambio de variable x(lx) t = lx. Etoces dt = dx y, sustituyedo, os queda x x(lx) dx = t dt = t +C = lx +C. E segudo lugar, dado cualquier b > e, calculamos Barrow (Teorema..3): b e x(lx) dx = Fialmete, tomamos límites cuado b : lím b b e ( dx = lím ) x(lx) b lb + b [ ] b = lx e lb + le = lb +. e dx mediate la Regla de x(lx) = lím b lb + = 0 + =. Luego la itegral impropia dx coverge y vale. e x(lx) x (iv) Calculamos la primitiva + x dx mediate el cambio de variable t = + x. E efecto, teemos dt = xdx y, sustituyedo, queda: x + x dx = t dt = t dt = l t +C = l( + x ) +C. Fijado a < 0, podemos aplicar la Regla de Barrow (Teorema..3) obteiedo: 0 [ x l( + x ] 0 + x dx = ) = l( + 0 ) l( + a ) = l( + a ). a Tomado límites cuado a, teemos: lím a 0 a a x dx = lím + x l( + a ) =, a
126 0 Itegrales así que la itegral impropia 0 x dx diverge. + x Ejercicio.3.3. Determia si las siguietes itegrales impropias coverge y, e tal caso, calcula su valor: (i) e lx x dx (ii) e 3x dx 0 (iii) 0 e x sexdx (iv) x dx SOLUCIÓN. (i) Para calcular la primitiva utilizamos el cambio de variable t = l x. Etoces dt = dx y sustituyedo obteemos: x lx x dx = t dt = t (lx) +C = +C. E segudo lugar, para cada b > e calculamos la itegral Barrow (Teorema..3): b e lx x dx = [ (lx) ] b e = (lb) Fialmete, tomamos límites cuado b : b lím b e lx x (le) b e lx x = (lb) (lb) dx = lím b =, lx luego la itegral impropia dx diverge. e x (ii) Haciedo el cambio de variable t = 3x, teemos dt = 3dx y e 3x dx = 3 Para cada b > 0, calculamos la itegral b 0 e 3x dx = e t dt = et +C = e 3x 3 3 +C. b 0 ] b [ e 3x Tomado límites cuado b, obteemos: 3 0 dx mediate la Regla de. e 3x dx aplicado la Regla de Barrow: = e 3b 3 + e0 3 = e 3b. 3 b lím e 3x e 3b dx = lím = b 0 b 3 3.
127 .3 Itegrales impropias Por tato, la itegral impropia coverge y 0 e 3x dx = 3. (iii) La primitiva e x sexdx se puede calcular mediate el método de itegració por partes. Alterativamete, vamos a utilizar la primitiva e x sexdx = ex (sex cosx) +C (.) que ya habíamos obteido e el Ejercicio..4(iv) (usado itegració por partes). Aplicamos el cambio de variable t = x a la primitiva origial. Etoces dt = dx y sustituyedo os queda: e x sexdx = e t se( t)dt ( ) = e t set dt (.) = (.) = et (set cost) +C = e x (se( x) cos( x)) +C ( ) = e x (sex + cosx) +C, dode las igualdades co ( ) so cosecuecia de que la fució seo es impar y la fució coseo es par, es decir, se( α) = se α y cos( α) = cos α para todo α R. Ahora, para cada b > 0, aplicamos la Regla de Barrow para obteer b 0 e x sexdx = Como lím b e b = 0 y [ ] b e x (sex + cosx) = 0 = e b (seb + cosb) + e0 (se0 + cos0) seb + cosb seb + cosb para todo b R, tambié se cumple lím b e b (seb + cosb) = 0. Por tato: b lím e x e b (seb + cosb) sexdx = lím b 0 b Así, la itegral impropia coverge y 0 e x sexdx =. = e b (seb + cosb). =. (iv) Aplicamos el cambio de variable t = x, de maera que dt = dx y 4 + x dx = 4 + 4t dt = +t dt = arctat +C = ( x ) arcta +C.
128 Itegrales Dado cualquier a < 0, calculamos la itegral 0 a 0 [ ( x ) ] x dx = arcta = a arcta(0) a ) arcta( a a dx mediate la Regla de Barrow: 4 + x Fialmete, tomamos límites cuado a : 0 ( a ) lím dx = lím a 4 + x a arcta = π 4. Luego la itegral impropia coverge y x dx = π 4. = arcta ( a Ejercicio.3.4. Estudia la covergecia de la siguiete itegral impropia e fució del valor del parámetro p, que puede ser u úmero real cualquiera: e x(lx) p dx SOLUCIÓN. E primer lugar, hallamos la primitiva ). dx mediate el cambio de x(lx) p variable t = lx. Etoces dt = dx y al sustituir obteemos: x t p+ x(lx) p dx = t p dt = si p (lx) p+ si p p + = p + l t si p = l lx si p = E vista de este resultado, vamos a distiguir dos casos. CASO p. Para cada b > e, aplicamos la Regla de Barrow para calcular b [ (lx) p+ ] b x(lx) p dx = = (lb) p+ p + p + (le) p+ p + = (lb) p+ p + + p. e Teiedo e cueta que e lím b (lb) p+ = 0 si p > si p < deducimos: b lím b e x(lx) p dx = si p > p si p <
129 .3 Itegrales impropias 3 Por tato, la itegral impropia dx coverge si p > y diverge si p <. e x(lx) p CASO p =. Para cada b > e, aplicamos la Regla de Barrow para calcular b e xlx dx = [l(lx)]b e = l(lb) l(le) = l(lb). Tomado límites cuado b, resulta que luego la itegral impropia b lím dx = lím l(lb) =, b e xlx b e dx diverge. xlx Ejercicio.3.5. Demuestra que las siguietes itegrales impropias coverge y calcula su valor: (i) 0 x e 3x dx (ii) 0 3 x cosxdx SOLUCIÓN. (i) Calculamos la primitiva mediate itegració por partes eligiedo u = x y dv = e 3x dx, de maera que du = xdx, v = e3x 3 y así: x e 3x dx = udv = uv vdu = x e 3x xe 3x dx. 3 3 A esta última primitiva le aplicamos el método de itegració por partes tomado u = x y dv = e 3x dx, así que du = dx, v = e3x 3 Por tato: xe 3x dx = udv = uv x e 3x dx = x e 3x ( xe 3x 3 3 y os queda: vdu = xe3x e3x 9 ) +C = e3x 3 e 3x dx = xe3x 3 e3x 9 +C. ( x x 3 + ) +C. 9 A cotiuació, para cualquier a < 0, calculamos la itegral e el itervalo [a,0]: 0 a [ e x e 3x 3x dx = 3 ( x x 3 + )] 0 = ( 9 a 7 e3a a a ). 9
130 4 Itegrales Aplicado la Regla de L Hôpital (Teorema.3.6), se comprueba fácilmete que e 3a ( lím a a a ) = 0 9 y, por tato, 0 lím x e 3x dx = a a 7. 0 Luego la itegral impropia x e 3x dx coverge y vale 7. (ii) Para calcular la primitiva, aplicamos el método de itegració por partes eligiedo u = 3 x y dv = cosxdx, de maera que du = l3 3 x dx, v = sex y os queda: 3 x cosxdx = udv = uv vdu = 3 x sex + l3 3 x sexdx. (.) A esta última primitiva le podemos aplicar de uevo el método de itegració por partes eligiedo u = 3 x y dv = sexdx. Etoces du = l3 3 x dx, v = cosx y así: 3 x sexdx = 3 x cosx l3 3 x cosxdx. (.3) Llamado I = 3 x cosxdx y sustituyedo (.3) e (.), deducimos la ecuació: I = 3 x sex + l3 ( 3 x cosx l3 I ). Despejado I e esta ecuació, obteemos la primitiva buscada: 3 x cosxdx = 3 x (sex l3 cosx) + (l3) +C. b 0 A cotiuació, para cualquier b > 0, calculamos la itegral e el itervalo [0,b]: [ 3 3 x x ] b (sex l3 cosx) cosxdx = + (l3) = 3 b (seb l3 cosb) l3 + (l3) + + (l3). Fialmete, como lím b 3 b = 0 y seb l3 cosb seb + l3 cosb + l3 para todo b > 0, tambié teemos lím 3 b (seb l3 cosb) = 0 y así deducimos que b lím Por tato, la itegral impropia b b x cosxdx = l3 + (l3). 3 x cosxdx es covergete y vale l3 + (l3).
131 .3 Itegrales impropias 5 Ejercicio.3.6. Utiliza los Criterios de Comparació para determiar si las siguietes itegrales impropias coverge: (i) (iii) SOLUCIÓN. (i) Teemos + x 3 dx x + x 7 dx lím x + x 3 x 3/ (ii) 0 + x dx ( sex ) (iv) dx x π = (0,). Como dx coverge (Ejemplo.3.4), el Criterio de Comparació II (Proposició.3.7) asegura que la itegral impropia dx tambié coverge. x3/ + x 3 Como (ii) Observamos e primer lugar que x lím x + x x = (0,). dx diverge (Ejemplo.3.4), podemos aplicar el Criterio de Comparació II (Proposició.3.7) para deducir que + x dx tambié diverge. Segú la Observació.3., esto último equivale a decir que la itegral impropia (iii) Teemos lím x x + x 7 x 5/ = (0,). 0 dx diverge. + x Teiedo e cueta que dx coverge (Ejemplo.3.4), el Criterio de Comparació II (Proposició.3.7) os asegura que dx coverge. x5/ x + x 7 (iv) Para cualquier x 0 teemos: sex = (sex) = ( sex ) (sex) = x x x.
132 6 Itegrales Como dx coverge (Ejemplo.3.4 y Observació.3.), el Criterio de Comparació I (Proposició.3.7) garatiza la covergecia de dx. π x ( sex ) x Ejercicio.3.7. Justifica razoadamete si es cierta o falsa la siguiete afirmació: La regió a la derecha del eje OY, compredida etre la gráfica de la fució f (x) = xe x3 y el eje OX, tiee u área ifiita. SOLUCIÓN. Como f (x) 0 para todo x 0, la preguta es equivalete a determiar si la itegral impropia 0 π f (x)dx diverge. Si itetamos calcular la primitiva de f (x) os ecotramos co dificultades, así que vamos a abordar el problema mediate el Criterio de Comparació I (Proposició.3.5). Observamos que x = x 3 x = e x3 e x = xe x3 xe x. (.4) Defiimos la fució g(x) = xe x. Vamos a comprobar, usado la defiició, que la itegral impropia g(x) dx es covergete. E efecto, mediate el cambio de variable t = x (dt = xdx) calculamos la primitiva: xe x dx = e t dt = et +C = e x +C. Para cualquier b >, la Regla de Barrow (Teorema..3) os da b [ xe x dx = e x] b = e e b. Tomado límites cuado b, como lím b e b = 0, obteemos Por tato, deducimos que b e e b lím xe x dx = lím b b = e. g(x) dx coverge. Teiedo e cueta (.4) y el Criterio de Comparació I, f (x)dx coverge. Luego Observació.3.). Así que la afirmació del euciado es falsa. 0 f (x) dx tambié coverge (aplicamos la
133 .4 Aproximació mediate métodos uméricos 7.4. Aproximació mediate métodos uméricos Coteidos Método del Trapecio. Método de Simpso. Aexos: Métodos de Mote Carlo. Teoría Esta lecció se dedica al estudio de alguos métodos uméricos que permite calcular aproximadamete la itegral Método del Trapecio b a f (x)dx de ua fució cotiua f : [a,b] R. Dado N, sea l(x) la fució iterpoladora lieal a trozos de f (x) e los putos de abscisas x k = a + k b a, k = 0,,...,, que divide el itervalo [a,b] e subitervalos [x k,x k ] de logitud b a. Fijado uo de estos subitervalos, podemos aproximar xk xk f (x)dx l(x)dx. x k x k Es secillo comprobar que xk l(x)dx = b a ( f (xk ) + f (x k ) ). x k Si f (x) 0 para todo x [x k,x k ], etoces l(x)dx es el área de u trapecio x k de altura b a y bases f (x k ) y f (x k ), véase la Figura.8 e la págia 8. Si repetimos el procedimieto e cada subitervalo [x k,x k ], obteemos la siguiete estimació de la itegral de f e [a,b]: b a f (x)dx = xk k= x k f (x)dx k= = b a xk xk l(x)dx = x k ( f (a) + f (x ) f (x ) + f (b) ).
134 8 Itegrales Figura.8: Gráficas de f (x) = se(x ) + y la fució lieal que coicide co f e 0 y. E violeta, el trapecio delimitado por la gráfica de dicha fució lieal, el eje OX y las rectas x = 0 y x =. Si f (x) 0 para todo x [a,b], la estimació aterior es la suma de las áreas de trapecios, véase la Figura.9. Figura.9: Método del Trapecio aplicado a f (x) = se(x ) + e [0,] co = subitervalos. Proposició.4. (Fórmula del Método del Trapecio). La aproximació de que se obtiee mediate el Método del Trapecio co subitervalos es: Trapecio ( f ) = b a ( f (a) + f (x ) f (x ) + f (b) ). b a f (x)dx
135 .4 Aproximació mediate métodos uméricos 9 Veamos u ejemplo: Ejemplo.4.. Calculamos aproximadamete l = Trapecio co 3 y 5 subitervalos, respectivamete. dx mediate el Método del x Solució. Trabajamos co f (x) =. Comezamos co = 3 subitervalos. Etoces x x 0 =, x = 4 3, x = 5 3, x 3 = y la aproximació obteida aplicado la fórmula del Método del Trapecio es Trapecio 3 ( f ) = 3 ( f () + f ( ) 4 + f 3 ( ) 5 3 = 6 Por otro lado, e el caso de = 5 subitervalos teemos ) + f () = ( x 0 =, x = 6 5, x = 7 5, x 3 = 8 5, x 4 = 9 5, x 5 =. La aproximació que da la fórmula del Método del Trapecio es Trapecio 5 ( f ) = ( f () + f 5 = 0 ( ) 6 + f 5 ( ) 7 5 ( f ) ( ) 8 + f 5 ) = 7 0 = 0.7. ( ) ) 9 + f () = 5 = = Esta aproximació es mejor que la obteida co = 3: el valor exacto (redodeado a 4 cifras decimales) de l es A la hora de aproximar b f (x)dx Trapecio ( f ) pa- pregutas que debemos respoder: ( a ) Podemos dar ua cota superior del error absoluto ra valores cocretos de? a f (x) dx mediate el Método del Trapecio, surge alguas b a ( a ) Fijado cualquier ε > 0, podemos determiar u úmero de subitervalos para que dicho error sea meor que ε?
136 30 Itegrales La proposició siguiete ayuda a respoder estas pregutas. Proposició.4.3 (Error e el Método del Trapecio). Si f es de clase C e [a,b] y M > 0 es ua costate tal que f (x) M para todo x [a,b], etoces b f (x)dx Trapecio ( f ) (b a)3 M para todo N. Por tato: a b lím Trapecio ( f ) = f (x)dx. a Vamos a ilustrar este resultado co u par de ejemplos. Ejemplo.4.4. Determiamos el úmero de subitervalos ecesarios para aproximar l = x dx mediate el Método del Trapecio co error absoluto meor que 0 4. Solució. La seguda derivada de f (x) = x es f (x) = x 3, así que f (x) = f (x) para todo x > 0. Como f (x) es estrictamete decreciete e (0,), teemos f (x) f () = para todo x. Por tato, M = cumple f (x) M para todo x [,]. Segú la acotació del error e el Método del Trapecio (Proposició.4.3), teemos x dx Trapecio ( f ) ( )3 M = 6 para todo N. Así, para ecotrar u N que cumpla x dx Trapecio ( f ) < 0 4 sólo ecesitamos ecotrar u N tal que 6 < 0 4. Observamos que 6 < < 5000 < Como 40.8, podemos tomar = 4 para obteer 3 x dx Trapecio 4 ( f ) < <. 3
137 .4 Aproximació mediate métodos uméricos 3 Aplicado la fórmula del Método del Trapecio co = 4 (Proposició.4.), podemos calcular Trapecio 4 ( f ) = Ejemplo.4.5. Calculamos aproximadamete se(x )dx mediate el Método del Trapecio co error absoluto meor que Solució. Trabajamos co la fució f (x) = se(x ). Derivado dos veces, teemos: Para cualquier x R se cumple f (x) = xcos(x ), f (x) = cos(x ) 4x se(x ). f (x) = cos(x ) 4x se(x ) () cos(x ) + 4x se(x ) = = cos(x ) + 4x se(x ) () + 4x. (.5) E efecto, () es cosecuecia de la desigualdad triagular, mietras que () es cosecuecia de que seα y cosα para todo α R. Combiado (.5) co el hecho de que +4x 6 para todo x [0,], deducimos que f (x) 6 para todo x [0,], así que podemos tomar M = 6 e este ejemplo. E vista de la Proposició.4.3, teemos se(x )dx Trapecio ( f ) ( 0)3 M = para todo N. 0 Por tato, para ecotrar u N que cumpla se(x )dx Trapecio ( f ) < basta ecotrar u N tal que < 0 3. Observamos que < < 500 <. Así, podemos tomar = 3 ( 500.3) para obteer se(x )dx Trapecio 3 ( f ) < Fialmete, calculamos la aproximació aplicado la fórmula del Método del Trapecio co = 3 (Proposició.4.): Trapecio 3 ( f ) =
138 3 Itegrales Método de Simpso El método se basa e la aproximació de f (x) mediate iterpolació a trozos utilizado poliomios de grado. Para ello itroducimos la siguiete defiició: Defiició.4.6. Llamamos fució iterpoladora cuadrática a trozos de f e los putos de abscisas a = x 0 < x <... < x = b a la fució C : [a,b] R defiida a trozos que, para cada k =,...,, coicide e todo el itervalo [x k,x k ] co el poliomio iterpolador de f e los putos de abscisas {x k,x k,x k }. DESCRIPCIÓN DEL MÉTODO DE SIMPSON: Dado N, sea C (x) la fució iterpoladora cuadrática a trozos de f (x) e los putos de abscisas x i = a + i b a, i = 0,,...,. Fijado u subitervalo de la forma [x k,x k ], podemos aproximar xk x k f (x)dx xk x k C (x)dx. La expresió de C (x) e este subitervalo se puede calcular fácilmete y, a partir de dicha expresió, se puede evaluar la itegral xk C (x)dx = b a x k 6 ( f (xk ) + 4 f (x k ) + f (x k ) ). Si repetimos el procedimieto e cada subitervalo [x k,x k ], obteemos la siguiete estimació de la itegral de f e [a,b]: b a f (x)dx = xk k= f (x)dx x k ( = b a 6 xk C (x)dx = k= x k f (a) + 4 k= f (x k ) + f (x k ) + f (b) k= Véase las Figuras.0 e la págia 33 para ua ilustració gráfica del método. ).
139 .4 Aproximació mediate métodos uméricos 33 Figura.0: Método de Simpso aplicado a f (x) = se( x) + e [0,0] co = y =. Proposició.4.7 (Fórmula del Método de Simpso). La aproximació de que se obtiee mediate el Método de Simpso co parábolas es: Simpso ( f ) = b a 6 ( f (a) + 4 k= ) f (x k ) + f (x k ) + f (b). k= A cotiuació aplicamos el Método de Simpso a la itegral del Ejemplo.4.. Ejemplo.4.8. Calculamos aproximadamete l = Simpso co y 4 parábolas, respectivamete. b a f (x)dx dx mediate el Método de x
140 34 Itegrales Solució. Sea f (x) =. Tomado =, teemos x x 0 =, x = 5 4, x = 3, x 3 = 7 4, x 4 =, y la aproximació obteida aplicado la fórmula del Método de Simpso es Simpso ( f ) = ( f () + 4 f 6 = ( ) f 4 ( ) 7 4 ( Por otro lado, e el caso de = 4 teemos + f ) ( ) ) 3 + f () = = = x 0 =, x = 9 8, x = 5 4, x 3 = 8,... x 7 = 5 8, x 8 =. Calculamos la aproximació que os da el Método de Simpso: Simpso 4 ( f ) = ( f () + 4 f (x ) + 4 f (x 3 ) + 4 f (x 5 ) + 4 f (x 7 ) f (x ) + f (x 4 ) + f (x 6 ) + f () ) = Esta aproximació es mejor que la obteida co = : el valor exacto (redodeado a 4 cifras decimales) de l es Observamos además que la aproximació Simpso ( f ) (que requiere 5 evaluacioes de f ) ya es bastate mejor que la aproximació Trapecio 5 ( f ) (obteida e el Ejemplo.4. y que requiere 6 evaluacioes de f ). Dispoemos del siguiete resultado para cotrolar el error cometido al aproximar itegrales mediate el Método de Simpso. Proposició.4.9 (Error e el Método de Simpso). Si f es de clase C 4 e [a,b] y M > 0 es ua costate tal que f (4) (x) M para todo x [a,b], etoces b a f (x)dx Simpso ( f ) (b a)5 M para todo N. 80 () 4 Por tato: b lím Simpso ( f ) = f (x)dx. a
141 .4 Aproximació mediate métodos uméricos 35 Ejemplo.4.0. Calculamos aproximadamete la itegral Método de Simpso: ( π ) cos x dx mediate el (i) co 3 parábolas, dado ua cota superior del error absoluto cometido; (ii) co error absoluto meor que 0 4. Solució. (i) E este caso = 3 y ecesitamos evaluar la fució f (x) = cos ( π x ) e x 0 =, x = 3, x = 3, x 3 = 0, x 4 = 3, x 5 = 3, x 6 =. La aproximació pedida es Simpso 3 ( f ) = ( ) ( f () + 4 f (x ) + 4 f (x 3 ) + 4 f (x 5 ) + f (x ) + f (x 4 ) ) = 6 3 = Para hallar ua cota superior del error absoluto de dicha aproximació, calculamos la derivada cuarta de f (x): f (x) = π se ( π x ), f (x) = π 4 cos ( π x ), f (3) (x) = π3 8 se ( π x ), f (4) (x) = π4 6 cos ( π x ). Observamos etoces que la costate M = π4 6 cumple f (4) (x) M para todo x [,] (porque cosα para todo α R). Por tato, la Proposició.4.9 garatiza que f (x)dx Simpso 3 ( f ) ( ( )) π4 6 = π Así, por ejemplo, ua cota del error cometido co 3 parábolas es (ii) Segú la Proposició.4.9, se cumple f (x)dx Simpso ( f ) ( ( ))5 80 () 4 π4 6 = π para todo N. Buscamos u N tal que π < 0 4 o, equivaletemete > 4 04 π
142 36 Itegrales Luego es suficiete co tomar = 6. E este caso, teemos que evaluar f e x 0 =, x = 5 6, x = 3,... x = 5 6, x =, y la aproximació que proporcioa el Método de Simpso es Simpso 6 ( f ) = ( ) ( f ( ) + 4 f (x ) f (x ) f (x ) f (x 0 ) + f () ) = Los métodos de Mote Carlo de itegració umérica se basa e la utilizació de úmeros aleatorios para obteer aproximacioes de la itegral. A diferecia de los métodos del Trapecio y Simpso, que so determiistas, los métodos de Mote Carlo so probabilistas y geeralmete proporcioa aproximacioes distitas e cada ejecució del algoritmo, auque se utilice los mismos datos de etrada. Aexo A: Método de Mote Carlo I ( acertar o fallar ) Se puede aplicar cuado f (x) 0 para todo x [a, b]. E primer lugar, ecesitamos elegir u úmero d > 0 tal que f (x) d para todo x [a,b]. Fijamos N (dato de etrada del algoritmo) y PROCEDEMOS:. Se toma al azar putos (x i,y i ) e el rectágulo [a,b] [0,d]. Es decir, x i [a,b] e y i [0,d] para todo,...,.. Para cada i =,..., comprobamos si se cumple la desigualdad y i f (x i ). Llamamos p al úmero de ídices i tales que y i f (x i ). 3. Etoces es ua aproximació de p (b a)d b a f (x)dx. (dato de salida del algoritmo) IDEA DEL MÉTODO: Para valores grades de, teemos p área bajo la gráfica de f área del rectágulo [a, b] [0, d] véase la Figura. e la págia 37. = b f (x)dx a (b a)d,
143 .4 Aproximació mediate métodos uméricos 37 Figura.: Aproximació de la itegral de f (x) = x e [,] mediate el Método de Mote Carlo I co = 000 putos y tomado d =. Los putos verdes (resp. rojos) queda por debajo (resp. ecima) de la gráfica de f. Aexo B: Método de Mote Carlo II ( media de la muestra ) Fijamos N (dato de etrada del algoritmo) y PROCEDEMOS:. Se toma al azar úmeros x i e el itervalo [a,b]. Es decir, x i [a,b] para todo i =,...,.. Etoces f (x ) f (x ) (b a) (dato de salida del algoritmo) es ua aproximació de b a f (x)dx. IDEA DEL MÉTODO: Para valores grades de, Ejercicios f (x ) f (x ) b a b a f (x)dx. Ejercicio.4.. Sea f : [0, ] R ua fució cotiua tal que ( ) ( ) 3 f = f = α. 4 4
144 38 Itegrales Determia el valor de α sabiedo que Trapecio ( f ) = y Trapecio 4 ( f ) = 7 4. SOLUCIÓN. Para =, la fórmula del Método del Trapecio (Proposició.4.) es = Trapecio ( f ) = 0 ( ( ) ) f (0) + f + f () = ( ( ) ) f (0) + f + f (), 4 de dode ( 8 = f (0) + f Por otro lado, la fórmula del Método del Trapecio para = 4 es 7 4 = Trapecio 4 ( f ) = 0 ( ( ) ( ) ( ) 3 f (0) + f + f + f = ( ( f (0) + f 8 luego 4 = f (0) + f ) + f (). (.6) ) + f () = ) + f () + 4α ), ( ) + f () + 4α. (.7) Sustituyedo la igualdad (.6) e (.7), obteemos 4 = 8 + 4α, así que α = 3. Ejercicio.4.. Al aplicar el Método del Trapecio co subitervalos para aproximar la itegral 0 f (x)dx (dode f (x) es ua fució descoocida), obteemos el valor. Si por el cotrario aplicamos el Método de Simpso co ua parábola, obteemos el valor 4. Cuáto vale f ()? SOLUCIÓN. Si llamamos x 0 = 0, x = y x =, etoces = Trapecio ( f ) = 0 ( f (x0 ) + f (x ) + f (x ) ) = ( f (x 0 ) + f (x ) + f (x ) ), luego 4 = f (0) + f () + f (). (.8) Por otro lado, teemos 4 = Simpso ( f ) = 0 ( f (x0 ) + 4 f (x ) + f (x ) ) = 3 3 ( f (x 0 ) + 4 f (x ) + f (x ) ), así que 6 = f (0) + 4 f () + f (). (.9) Si restamos (.8) a (.9), obteemos la igualdad = f (), por lo que f () =.
145 .4 Aproximació mediate métodos uméricos 39 Ejercicio.4.3. Demuestra que Simpso ( f ) = b a f (x)dx para cualquier poliomio f (x) de grado meor o igual que 3 y cualquier itervalo [a,b]. SOLUCIÓN. Escribimos f (x) = Ax 3 + Bx +Cx + d. Defiiedo las fucioes g(x) = x 3 y h(x) = Bx +Cx + d, de maera que f (x) = Ag(x) + h(x). Es secillo comprobar que Simpso ( f ) = A Simpso (g) + Simpso (h). (.30) Por la propia defiició, el Método de Simpso proporcioa el valor exacto de la itegral para poliomios de grado meor o igual que. E particular, Simpso (h) = b Por otro lado, aplicado la Regla de Barrow obteemos b a [ x x 3 4 dx = 4 ] b a a h(x) dx. (.3) = b4 a 4. 4 Y ahora el Método de Simpso aplicado a g(x) os da: Simpso (g) = b a ( ( ) ) a + b f (a) + 4 f + f (b) = 6 ( = b a ( ) ) a + b 3 a b 3 = b a ( a 3 + ( a 3 + 3a b + 3ab + b 3) + b 3) = 6 = b a 4 ( a 3 + a b + ab + b 3) = 4 Sustituyedo (.3) y (.3) e la igualdad (.30), deducimos b b Simpso ( f ) = A x 3 dx + h(x)dx = a a como se quería demostrar. ( a 3 b + a b + ab 3 + b 4 a 4 a 3 b a b ab 3) = b a = b4 a 4 4 = b a x 3 dx. (.3) ( Ax 3 + h(x) ) b dx = f (x)dx, a
146 40 Itegrales Ejercicio.4.4. Se cosidera la fució f (x) = se (N!πx), co N N fijo. (i) Utiliza la Regla de Barrow para demostrar que f (x)dx =. 0 [Nota: recuerda que se α = cos(α) para todo α R.] (ii) Demuestra que, si aplicamos el Método del Trapecio para aproximar esta itegral, etoces Trapecio ( f ) = 0 para todo N. (iii) E vista de lo aterior, qué ocurre cuado N es muy grade? SOLUCIÓN. (i) Comezamos calculado la primitiva cos(n!πx) se (N!πx)dx = dx mediate el cambio de variable t = N!πx. Etoces dt = N!π dx y os queda cos(n!πx) cost dx = 4N!π dt = ( cost)dt = 4N!π = ( ) ( ) x t set +C = N!πx se(n!πx) +C = 4N!π 4N!π se(n!πx) +C. 4N!π Ahora aplicamos la Regla de Barrow (Teorema..3) para calcular la itegral: [ x f (x)dx = se(n!πx) ] ( ) ( ) se(n!π ) 0 se(n!π 0) = = 4N!π 4N!π 4N!π, 0 ya que se(mπ) = 0 para todo m N. 0 (ii) Fijamos N co N. Para calcular Trapecio ( f ) evaluamos f e los putos x k = k para k = 0,,...,, obteiedo ( ) ( k f (x k ) = f = se N!π k ) ( ) N! = se kπ = 0, ya que N! N y se(mπ) = 0 para todo m N. Ahora aplicamos la fórmula del Método del Trapecio (Proposició.4.): Trapecio ( f ) = 0 ( f (x0 ) + f (x ) f (x ) + f (x ) ) = 0,
147 .4 Aproximació mediate métodos uméricos 4 como se quería demostrar. (iii) Segú lo que hemos visto e los apartados (i) y (ii), el Método del Trapecio proporcioa u resultado (0) bastate alejado del valor exacto de la itegral ( ) cuado se utiliza u úmero de subitervalos meor o igual que N. Así, para valores grades de N ecesitaremos utilizar muchos subitervalos para coseguir ua buea aproximació de la itegral mediate el Método del Trapecio. Ejercicio.4.5. Determia, e cada uo de los casos siguietes, el úmero de subitervalos ecesarios para obteer, mediate el Método del Trapecio, ua aproximació de la itegral dada co error absoluto meor que : (i) π/6 π/6 cosxdx (ii) 3 5 x dx SOLUCIÓN. (i) La seguda derivada de f (x) = cosx es f (x) = cosx, así que f (x) = cosx para todo x R. Por tato, M = cumple f (x) M para todo x [ π 6, π 6 ]. Ahora, segú la acotació del error e el Método del Trapecio (Proposició.4.3), teemos π/6 π/6 cosxdx Trapecio ( f ) Por tato, para determiar u N que cumpla π/6 π/6 sólo ecesitamos ecotrar u N tal que (π/6 + π/6)3 M = π3 34 para todo N. cosxdx Trapecio ( f ) < π 3 34 < Como π 3 34 < π < 38.3 podemos tomar = 39 para obteer el grado de precisió deseado. π <,
148 4 Itegrales (ii) Derivamos f (x) = dos veces: 5 x f (x) = (5 x), f (x) = (5 x) 3. La fució f (x) es positiva y estrictamete creciete e el itervalo (,5). E particular, M = f (3) = 4 cumple f (x) M para todo x [,3]. La acotació del error e el Método del Trapecio (Proposició.4.3) es 3 5 x dx Trapecio ( f ) (3 )3 M = 48 para todo N. Así, para determiar u N que cumpla 3 5 x dx Trapecio ( f ) < sólo hay que ecotrar u N tal que 48 < o, equivaletemete, 500 < Como 64.5, podemos tomar = Ejercicio.4.6. Determia el úmero de parábolas ecesarias para obteer, mediate el Método de Simpso, ua aproximació de cada ua de las itegrales del Ejercicio.4.5 co error absoluto meor que SOLUCIÓN. (i) Comezamos co la itegral cuarta de f (x) = cosx es f (4) (x) = cosx, así que π/6 π/6 f (4) (x) = cosx para todo x R. cosxdx. Observamos que la derivada Podemos tomar M = e la acotació del error de la Proposició.4.9, obteiedo π/6 f (x)dx Simpso ( f ) (π/6 ( π/6))5 π 5 80 () 4 = π/6 para todo N. Por tato, para determiar u N que cumpla π/6 f (x)dx Simpso ( f ) < π/6
149 .4 Aproximació mediate métodos uméricos 43 sólo teemos que ecotrar u N tal que π < Como π < π < π <, podemos tomar = 4 para obteer la precisió requerida. 3 (ii) Pasamos ahora a estudiar dx. Derivamos f (x) = cuatro veces: 5 x 5 x f (4) (x) = 4 (5 x) 5. Teiedo e cueta que la fució f (4) (x) es positiva y estrictamete creciete e el itervalo (,5), deducimos que la costate M = f (4) (3) = 3 4 cumple f (4) (x) M para todo x [,3]. E vista de la Proposició.4.3, teemos 3 f (x)dx Simpso ( f ) (3 )5 80 () = para todo N. Así, para determiar u N que cumpla 3 f (x)dx Simpso ( f ) < sólo hay que ecotrar u N tal que Luego podemos tomar = < o, equivaletemete, >
150 44 Itegrales.5. Apédice: Iterpolació Coteidos Poliomio iterpolador. Iterpolació a trozos. Teoría E esta lecció presetamos ua breve itroducció a los aspectos más básicos de la teoría de aproximació global de fucioes. E ocasioes se cooce los valores de ua fució e u cojuto de datos y se quiere estimar otro valor de la fució a partir de esos datos. Para resolver este problema, los métodos de iterpolació proporcioa poliomios aproximadores que coicide co la fució e el cojuto de datos coocidos. El teorema siguiete garatiza la existecia de dichos poliomios y proporcioa ua fórmula para calcularlos: Teorema.5.. Se cosidera + putos del plao co abscisas distitas dos a dos: (x 0,y 0 ), (x,y ),..., (x,y ). Etoces existe u úico poliomio P(x) de grado meor o igual que tal que P(x i ) = y i para todo i = 0,,...,. Dicho poliomio se llama poliomio iterpolador e los putos dados y se puede calcular mediate la fórmula P(x) = i=0 y i L i (x), dode L i (x) = j=0 j i x x j x i x j para todo i = 0,,...,. Veamos u primer ejemplo de poliomio iterpolador: Ejemplo.5.. Cálculo del poliomio iterpolador e los putos (0, ), (,), (, 7) y (3,).
151 .5 Apédice: Iterpolació 45 Figura.: Poliomio iterpolador e los putos (0, ), (, ), (, 7) y (3, ). Demostració. E este caso = 3 y x 0 = 0, x =, x = y x 3 = 3. Por tato: L 0 (x) = x x x x x x 3 = (x )(x )(x 3) x 0 x x 0 x x 0 x 3 6 L (x) = x x 0 x x x x 3 = x(x )(x 3) x x 0 x x x x 3 L (x) = x x 0 x x x x 3 = x(x )(x 3) x x 0 x x x x 3 L 3 (x) = x x 0 x x x x = x(x )(x ) x 3 x 0 x 3 x x 3 x 6 Sustituyedo estos poliomios y los valores y 0 =, y =, y = 7, y 3 = e la fórmula del Teorema.5., obteemos el poliomio iterpolador e el cojuto de putos dado: P(x) = y 0 L 0 (x) + y L (x) + y L (x) + y 3 L 3 (x) = 9x3 3x + x 6, 6 véase la Figura.. Los poliomios iterpoladores so ua herramieta útil para aproximar fucioes, como veremos a cotiuació. Defiició.5.3. Sea f ua fució defiida, al meos, e {x 0,x,...,x } R. Llamamos poliomio iterpolador de f e los putos de abscisas {x 0,x,...,x } al poliomio iterpolador e los putos (x 0, f (x 0 )), (x, f (x )),..., (x, f (x )).
152 46 Itegrales Ejemplo.5.4. Calculamos el poliomio iterpolador de la fució f (x) = sex + x 4 e los putos de abscisas { π,0, π 4 }. Demostració. E este ejemplo = y x 0 = π, x = 0, x = π 4. Así: L 0 (x) = x x x 0 x x x x 0 x = 8 L (x) = x x 0 x x 0 x x 3π x (x π 4 = 8 (x x x π + π L (x) = x x 0 x x = 6 (x x x 0 x x 3π + π Sustituyedo estos poliomios y los valores y 0 = f ) )( x π 4 ( π ) = + π4 ( π ) 6, y = f (0) = 0, y = f = + π4 4 56, e la fórmula del Teorema.5., obteemos el poliomio iterpolador: P(x) = y 0 L 0 (x) + y L (x) + y L (x) = ( ) ( ( 9 3/ π 4 7/ + 5 x + 3/ + 56 ) π 3 π 5) x 3 / π véase la Figura.3 para ua represetació cojuta de P(x) y f (x). Por defiició, el poliomio iterpolador coicide co la fució e el cojuto de putos que se ha usado para costruirlo. Para aalizar el error absoluto cometido al aproximar e el resto de putos, dispoemos de la siguiete acotació: Proposició.5.5 (Error del poliomio iterpolador). Sea {x 0,x,...,x } R, ) x a = mí{x 0,x,...,x } y b = máx{x 0,x,...,x }. Sea f ua fució de clase C + defiida, al meos, e el itervalo [a,b] y sea P(x) el poliomio iterpolador de f e los putos de abscisas {x 0,x,...,x }. Si M > 0 es ua costate tal que f (+) (x) M para todo x [a,b], etoces f (x) P(x) M ( + )! i=0 x x i para todo x [a,b]. (.33) )
153 .5 Apédice: Iterpolació 47 Figura.3: Poliomio iterpolador de f (x) = sex + x 4 e los putos de abscisas { π,0, π 4 }. Ejemplo.5.6. Se puede comprobar que el poliomio iterpolador de f (x) = sex e los putos de abscisas { π 4,0, π 8 } es ( ( 64 se π8 ) 9/ ) x + ( 6π se ( ) π P(x) = 8 + 3/ π ) x 3π. Este poliomio cumple: [ f (x) P(x) < 0.8 para todo x π 4, π ]. 8 Demostració. E este ejemplo =. La tercera derivada f (3) (x) = cosx cumple f (3) (x) para todo x R. Tomado M =, la acotació del error que os da la Proposició.5.5 es: f (x) P(x) 3! x + π x x π 4 8 para todo x [ π 4, π ]. (.34) 8 Si ahora teemos e cueta que x + π 3π 4 8, x π 4 y x π 3π 8 8 para todo x [ π, π ] 4 ( 3π 8 es la logitud del itervalo [ π 4, π ] 8 ), de la desigualdad (.34) se sigue que f (x) P(x) ( ) 3π 3! π 8 4 = 3π para todo x [ π 4, π 8 ].
154 48 Itegrales Para aproximar ua fució defiida e u itervalo, a veces es coveiete dividir dicho itervalo e subitervalos más pequeños y aplicar, e cada uo de ellos por separado, u método de iterpolació: esto se cooce como iterpolació a trozos. Defiició.5.7. Sea f : [a, b] R ua fució. Llamamos fució iterpoladora lieal a trozos de f e los putos de abscisas a = x 0 < x <... < x = b a la fució l : [a,b] R defiida a trozos que, para cada i =,...,, coicide e todo el itervalo [x i,x i ] co el poliomio iterpolador de f e los putos de abscisas {x i,x i }. Ejemplo.5.8. Sea l(x) la fució iterpoladora lieal a trozos de f (x) = cosx e los putos de abscisas {0, π 4, π, 3π 4,π} (véase la Figura.4). Etoces f (0.) = cos(0.) = y l(0.) = Demostració. Sea P el poliomio iterpolador de f e los putos de abscisas {0, π 4 }. Es secillo comprobar que dicho poliomio (de grado ) es P(x) = 4 π x +. Como 0. [0, π 4 ], teemos que l(0.) = P(0.) = La siguiete proposició os da ua cota superior del error absoluto cometido al aproximar los valores de ua fució mediate ua fució iterpoladora lieal a trozos. Proposició.5.9 (Error de la fució iterpoladora lieal a trozos). Sea f : [a,b] R ua fució de clase C y l : [a,b] R la fució iterpoladora lieal a trozos de f e los putos de abscisas a = x 0 < x <... < x = b. Si M > 0 es ua costate tal que f (x) M para todo x [a,b], etoces f (x) l(x) M 8 máx i=,..., x i x i para todo x [a,b]. (.35) Ejemplo.5.0. Cálculo de ua cota superior del error cometido al aproximar la fució f (x) = x cosx e el itervalo [0,3] mediate iterpolació lieal a trozos, utilizado 6 subitervalos de la misma logitud.
155 .5 Apédice: Iterpolació 49 Figura.4: Fució iterpoladora lieal a trozos de f (x) = cosx e los putos de abscisas {0, π 4, π, 3π 4,π}. Demostració. E este ejemplo = 6 y los putos a utilizar para costruir la fució iterpoladora lieal a trozos l(x) tiee abscisas x i = i (i = 0,,...,6) de maera que x i x i = 4 para todo i = 0,,...,6. Por otro lado, f (x) = ( x )cosx 4xsex. Como x 7 para todo x [0,3] y además sex, cosx, podemos aplicar la desigualdad triagular para deducir que f (x) ( x )cosx + 4xsex = x cosx + 4x sex = 9 para todo x [0,3]. Tomado ahora M = 9 e la desigualdad (.35) de la Proposició.5.9, obteemos: f (x) l(x) 9 8 = para todo x [0,3]. 4 Por tato, es ua cota superior del error cometido al aproximar f (x) mediate l(x) para cualquier x [0,3].
156 50 Itegrales La cota del error obteida e el ejemplo aterior o garatiza ua buea precisió e la aproximació. Para obteer aproximacioes razoables ecesitamos aumetar bastate el úmero de subitervalos, como ilustramos a cotiuació. Ejemplo.5.. Cálculo del úmero de subitervalos ecesarios para que, al aproximar la fució f (x) = x cosx e el itervalo [0,3] mediate iterpolació lieal a trozos, utilizado subitervalos de la misma logitud, el error cometido sea meor que 0.0. Demostració. Para u N arbitrario, los putos que usamos para costruir la correspodiete fució iterpoladora lieal a trozos l (x) tiee abscisas x i = i 3 (i = 0,,...,) y teemos x i x i = 9 para todo i = 0,,...,. Tomado (como e el ejemplo aterior) M = 9, la Proposició.5.9 os dice que f (x) l (x) = 7 8 para todo x [0,3]. Ahora ecesitamos ecotrar u N tal que 7 < 0.0 o, equivaletemete, > Por tato, = 47 garatiza u error absoluto meor que 0.0. Ejercicios Ejercicio.5.. Sea P(x) el poliomio iterpolador e los putos (0,0), (,α), (,3) y (,). Calcula el valor de α sabiedo que el coeficiete de x 3 e P(x) es 6. SOLUCIÓN. Como P(x) tiee grado 3, lo podemos escribir como P(x) = 6x 3 + ax + bx + c para ciertos coeficietes a,b,c R. Etoces: P(0) = 0 = c = 0 P() = 3 = 6 + a + b + c = 3 P() = = a + b + c =
157 .5 Apédice: Iterpolació 5 Resolviedo este sistema de ecuacioes, cocluimos que a = 0 y b = 7. Por tato, el poliomio iterpolador es P(x) = 6x 3 0x + 7x y así α = P ( ) = 6 ( ) 3 0 ( ) + 7 = 7 4. Ejercicio.5.3. Dada la fució f (x) = log 3 (x) se pide: (i) Calcula su poliomio iterpolador e los putos de abscisas { 3,,3,9}. (ii) Aproxima log 3 () mediate dicho poliomio y da ua cota del error cometido. (iii) Aproxima log 3 () mediate la fució iterpoladora lieal a trozos de f e los putos de abscisas { 3,,3,9} y da ua cota superior del error cometido. SOLUCIÓN. (i) E este caso = 3 y x 0 = 3, x =, x = 3 y x 3 = 9. Por tato: L 0 (x) = x x x x x x 3 = 7 (x )(x 3)(x 9) x 0 x x 0 x x 0 x 3 46 L (x) = x x 0 x x x x 3 = 3 ( x ) (x 3)(x 9) x x 0 x x x x L (x) = x x 0 x x x x 3 = ( x ) (x )(x 9) x x 0 x x x x L 3 (x) = x x 0 x 3 x 0 x x x 3 x x x x 3 x = 46 Sustituyedo estos poliomios y los valores y 0 = f ( x 3 ) (x )(x 3) ( ) =, y = f () = 0, y = f (3) =, y 3 = f (9) =, 3 e la fórmula del Teorema.5., obteemos el poliomio iterpolador pedido: P(x) = y 0 L 0 (x) + y L (x) + y L (x) + y 3 L 3 (x) = x3 69x + 676x (ii) La aproximació de f () = log 3 () que da el poliomio aterior es P() = 53 3 =
158 5 Itegrales Para dar ua cota superior del error absoluto f () P() ecesitamos la derivada cuarta de f (x) = log 3 (x) = lx. Derivado sucesivas veces: l3 f (x) = (l3)x, f (x) = (l3)x, f (3) (x) = (l3)x 3, f (4) (x) = 6 (l3)x 4. Observamos que f (4) (x) = 6 (l3)x 4 6 (l3) ( ) 4 = 486 l3 < [ ] para todo x 3,9. Tomado M = 486 y x = e la desigualdad (.33) de la Proposició.5.5: f () P() 486 4! = 4 = (iii) Si llamamos l(x) a la fució iterpoladora lieal a trozos de f e los putos de abscisas { 3,,3,9}, etoces l() = Q(), siedo Q el poliomio iterpolador de f e los putos de abscisas {, 3} (usamos dicho poliomio porque [, 3]). Es fácil ver que y así l() = Q() = 0.5. Q(x) = x Para dar ua cota superior del error absoluto f () l() vamos a aplicar la Proposició.5.5 al poliomio iterpolador Q(x) (es decir, tomado =, x 0 = y x = 3). La seguda derivada de f cumple f (x) = (l3)x = (l3)x (l3) = < para todo x [,3], l3 así que podemos elegir M = e la desigualdad (.33) de la Proposició.5.5: f () l() = f () Q() 3 = 0.5.! Ejercicio.5.4. Se dispoe de ua tabla de valores de la fució f (x) = e x + cosx e los putos de abscisas {0,0.5,...,3.5,4}. Da ua cota superior del error cometido al aproximar f (x) mediate iterpolació lieal a trozos, para cualquier x [0,4].
159 .5 Apédice: Iterpolació 53 SOLUCIÓN. Derivado f (x) = e x sex y f (x) = e x cosx. Por tato: f (x) e x + cosx = e x + cosx e 0 + = para todo x [0,4] (ya que la fució e x es decreciete y cosx para todo x R). Tomado M = e la desigualdad (.35) de la Proposició.5.9, deducimos que la fució iterpoladora lieal a trozos l(x) cumple para todo x [0,4]. f (x) l(x) 8 (0.5) = 6 = Ejercicio.5.5. Calcula el úmero de subitervalos ecesarios para que, al aproximar la fució f (x) = se(x ) e el itervalo [0,] mediate iterpolació lieal a trozos, utilizado subitervalos de la misma logitud, el error cometido sea meor que 0 3. SOLUCIÓN. Comezamos calculado la seguda derivada de la fució a iterpolar: f (x) = xcos(x ), f (x) = cos(x ) 4x se(x ). Por tato, f (x) cos(x ) + 4x se(x ) + 4 = 8 para todo x [0,]. Podemos tomar etoces M = 8 e la Proposició.5.9. Si llamamos l (x) a la fució iterpoladora lieal a trozos de f e los putos de abscisas x i = i (i = 0,,...,) deducimos que f (x) l (x) 8 8 ( ) = 9 para todo x [0,]. Por tato, ecesitamos ecotrar u N tal que 9 < 0 3. Esta desigualdad equivale a > 9000 = y, por tato, = 95 subitervalos sería suficietes para garatizar u error meor que 0 3. Ejercicio.5.6. Calcula el úmero de subitervalos ecesarios para que, al aproximar la fució f (x) = e x e el itervalo [0,5] mediate iterpolació lieal a trozos, utilizado subitervalos de la misma logitud, el error cometido sea meor que 0.0.
160 54 Itegrales SOLUCIÓN. Calculamos la seguda derivada de la fució: Por tato, f (x) = xe x, f (x) = (x )e x. f (x) = x e x 49 e 0 = 98 para todo x [0,5] (ya que x 49 para todo x [0,5] y la fució e x es decreciete e [0,)). Vamos a aplicar la Proposició.5.9 tomado M = 98. Si llamamos l (x) a la fució iterpoladora lieal a trozos de f e los putos de abscisas teemos f (x) l (x) 98 8 x i = i 5 (i = 0,,...,) ( ) 5 = 5 4 para todo x [0,5]. Buscamos u N tal que 5 4 < 0.0 o, equivaletemete, > 3065 = 75. Así, = 76 subitervalos garatiza u error meor que 0.0.
161 Capítulo 3 Series «OBJETIVOS» Aalizar la covergecia de series de térmios o egativos. Determiar el orde de magitud de las sumas parciales de series divergetes. Estudiar la covergecia de series alteradas. Calcular aproximadamete la suma de series covergetes. Utilizar poliomios y series de Taylor para aproximar fucioes. El tercer capítulo está dedicado a estudiar SERIES de úmeros reales. Las series so herramietas valiosas e Iformática a la hora de estudiar la eficiecia de algoritmos. Por ejemplo, si teemos ua lista de datos y llamamos t k al tiempo que se tarda e procesar el k-ésimo dato, etoces el tiempo que se tarda e procesar los primeros datos de la lista (uo detrás de otro) es T = t +t t = t k. k= Normalmete iteresa coocer el orde de magitud de T cuado crece. Por ejemplo, las técicas de aálisis de series mediate itegrales (que estudiaremos e la Lecció 3.) permite deducir que el algoritmo quicksort requiere u tiempo medio O( l ) para ordear ua lista de elemetos. E la Lecció 3. itroducimos los coceptos de serie covergete, serie divergete y suma de ua serie covergete. Estudiamos sus propiedades básicas (por ejemplo, la covergecia hacia 0 del térmio geeral de ua serie covergete) y los primeros ejemplos, como las series geométricas.
162 56 Series E la Lecció 3. mostramos cómo las itegrales puede ser ua herramieta útil e el estudio de las series. Comezamos aalizado las series armóicas geeralizadas y después estudiamos el Criterio Itegral para series de térmios o egativos. Además de examiar la covergecia divergecia de series, os cetramos e determiar el orde de magitud de la sucesió de sumas parciales (para series divergetes) y e el cálculo aproximado de la suma de series covergetes. E la Lecció 3.3 damos alguos criterios de comparació para determiar la covergecia de series de térmios o egativos y el orde de magitud de la sucesió de sus sumas parciales. Además, estudiamos la covergecia (y suma aproximada) de series alteradas mediate el Criterio de Leibiz. Para termiar, e la Lecció 3.4 presetamos el cocepto de poliomio y serie de Taylor de ua fució, calculamos los poliomios y series de Taylor de alguas fucioes elemetales y mostramos cómo se puede utilizar para aproximar localmete dichas fucioes.
163 3. Propiedades básicas Propiedades básicas Coteidos Series covergetes y divergetes. Series geométricas. Teoría El cocepto de serie aparece al itetar defiir la suma de ua sucesió (ifiita) de úmeros reales. La defiició siguiete formaliza dicha idea. Defiició 3... Sea a ua sucesió. (i) Se llama sumas parciales de la serie a a los úmeros: = S = a S = a + a... S = a + a a = (ii) Decimos que la serie = a k... k= a coverge si la sucesió de sumas parciales S es covergete. E tal caso, el límite lím S se llama suma de la serie y escribimos (iii) Decimos que la serie a = lím S. = a diverge si la sucesió S es divergete. = Observació 3... La sucesió de sumas parciales S tambié se puede defiir recurretemete por: S = a, S = S + a para todo. Veamos alguos ejemplos:
164 58 Series Ejemplo Se cosidera la sucesió a defiida por: a = 5, a = y a = 0 para todo 3. Las sumas parciales de la serie a so S = 5 y S = 7 para todo. = Así, la serie coverge y su suma vale 7. Ejemplo La serie diverge. = Demostració. La suma parcial -ésima de la serie es S = k = = k= ( + ), como vimos e el Ejemplo..6. Así, vemos que la sucesió S es divergete y, por defiició, la serie diverge. = Ejemplo 3..5 (Serie geométrica). Se llama serie geométrica de razó r R a Esta serie coverge si y sólo si r <. E tal caso, su suma es r = r = r. r. = Demostració. Fijamos N y comezamos calculado la suma parcial -ésima de la serie, es decir, S = r + r r. Distiguimos dos casos: Caso r =. Etoces r k = k = para todo k N y así S = r + r r = } +... {{ + } =. (3.) sumados Caso r. Multiplicado S por r obteemos: rs = r ( r + r r ) = r + r r + = = ( r + r + r r ) + r + r = S + r + r, es decir, rs = S + r + r. Equivaletemete, (r )S = r + r. Como r, e esta última igualdad podemos despejar S para deducir que S = r+ r r. (3.)
165 3. Propiedades básicas 59 Ahora estudiamos la covergecia de la sucesió S e fució de los valores de r: Si r teemos dos posibilidades: Si r = etoces S = (por (3.)), luego la sucesió S es divergete. Si r pero r, etoces la sucesió r + es divergete (véase el Ejemplo.3.3). Como r + = (r )S + r (por (3.)), deducimos que la sucesió S tambié es divergete. Por tato, cuado r la serie r diverge. = Si r < etoces lím r + = 0 (Ejemplo..) y, por tato, Así que la serie Esto completa la demostració. lím S (3.) r + r = lím r = 0 r r = r r. r coverge, co suma = r r. A cotiuació damos u ejemplo de serie telescópica. Ejemplo La serie = coverge y su suma vale. + Demostració. Descompoemos el térmio geeral e fraccioes simples: + = ( + ) = +. Ahora calculamos las sumas parciales utilizado la fórmula aterior: S = ( S = ) ( S 3 = ) +... ( S = ) + ( + ( ) = 3 3 ) ( ) = 4 4 ( ) ( ) ( ) = + +.
166 60 Series ( ) = lím = 0 =. Por tato, la serie co- + + Luego lím S = lím verge y + =. = E geeral, dada ua serie, puede ser difícil o icluso imposible dar ua fórmula explícita para la sucesió de sus sumas parciales (a diferecia de lo que ocurría e los ejemplos ateriores). Como cosecuecia, para estudiar la covergecia de series se suele utilizar métodos idirectos, que estudiaremos más adelate. Ahora damos alguas propiedades básicas de las series. Comezamos estudiado la suma de series y el producto de ua serie por u úmero real: Proposició 3..7 (Operacioes co series). (i) Si a coverge y α R, etoces αa tambié coverge y = = (ii) Si a y = = b coverge, etoces = = = αa = α = (a + b ) = = = a. (a + b ) tambié coverge y = a + Ejemplo Las series y = 3 coverge, co sumas y, respectivamete ( (Ejemplo 3..5). Por tato, la serie + 7 ) 3 tambié coverge, co suma ( = + 7 ) 3 = = + 7 = = b. 3 = + 7 = 9. El siguiete tipo de series juega u papel importate e la teoría: Defiició Decimos que ua serie para todo N. a es de térmios o egativos si a 0 =
167 3. Propiedades básicas 6 Proposició Sea a ua serie de térmios o egativos. Etoces: = (i) La sucesió de sus sumas parciales S es moótoa creciete. (ii) La serie Escribimos Demostració. a coverge la sucesió S está acotada. = a = cuado la serie diverge. = (i) Para cada teemos S = S + a S ya que a 0. (ii) es cosecuecia imediata de (i) y el Teorema... La covergecia o divergecia de ua serie o depede de sus primeros térmios, como poemos de maifiesto a cotiuació. Observació 3... Sea = a y = coicide, es decir, a = b para todo > m. Etoces: a coverge = b dos series cuyos térmios a partir del m-ésimo b coverge. = Demostració. Si llamamos S y T a las -ésimas sumas parciales de respectivamete, para cualquier > m teemos S = T = a k = k= b k = k= m k= m k= a k + b k + k=m+ k=m+ a k = S m + b k = T m + k=m+ k=m+ b k, b k. a y = b, = Luego S T = S m T m ( costate!) para todo > m. Por tato, la sucesió S es covergete si y sólo si la sucesió T es covergete. E las codicioes de la observació aterior, las sumas de ambas series puede ser distitas, aturalmete. Por ejemplo, e 3..5 hemos visto que la serie coverge, co suma. Por tato, la serie =
168 6 Series tambié coverge, pero su suma vale Defiició 3... Sea a ua sucesió defiida para 0. Etoces podemos cosiderar la serie a y las sumas parciales a a = a k para 0. = 0 k= 0 (i) Decimos que la serie caso, escribimos (ii) Decimos que la serie Observació Sea a coverge si la sucesió a k es covergete. E tal = 0 k= 0 a = lím = a k. 0 k= 0 a diverge si la sucesió a k es divergete. = 0 k= 0 a ua serie y 0 N. Etoces: = a coverge = = 0 a coverge. Demostració. La diferecia tato, la sucesió k= a k a k = k= 0 a k coverge si y sólo si la sucesió k= 0 a k es costate para todo 0. Por k= k= 0 a k coverge. Veamos u ejemplo ilustrado la defiició y observació ateriores: Ejemplo E geeral, tambié llamamos serie geométrica de razó r R a cualquier serie de la forma r, dode 0 N. Esta serie coverge si y sólo si r <. E = 0 tal caso: r = r0 = 0 r. Demostració. La covergecia o divergecia se puede deducir combiado el Ejemplo 3..5 co la Observació Para calcular la suma cuado r < y 0 >, basta
169 3. Propiedades básicas 63 observar que para todo > 0 teemos: k= 0 r k = r 0 + r r = = r 0 ( r + r r 0+ ) ( ) = r 0 r 0+ r r = r+ r 0, r dode la igualdad (*) se deduce de la fórmula (3.) e la págia 58. Tomado límites: r = lím = 0 r k r + r 0 = lím k= 0 r = 0 r 0 r = r0 r. Esto completa la demostració. Fializamos la lecció presetado el primer método idirecto para demostrar la divergecia de series. A saber, si para ua serie a se cumple que lím a 0, etoces = la serie diverge. E otras palabras: Proposició Si la serie a coverge, etoces lím a = 0. = Demostració. Llamamos S a la suma parcial -ésima de la serie, es decir, S = Etoces, para cada teemos S = S + a (Observació 3..), luego Si llamamos S = como se quería demostrar. Ejemplo La serie a k. k= a = S S. (3.3) a = lím S = lím S y tomamos límites e (3.3), obteemos: = lím a ( ) = lím S S = lím S lím S = S S = 0, = diverge, porque lím = 0. Si embargo, la codició lím a = 0 o garatiza la covergecia de la serie a. = Veamos u ejemplo:
170 64 Series Ejemplo La serie = diverge, auque lím = 0. Demostració. Fijamos N. Para cada k =,,..., teemos k, luego. k Etoces la suma parcial -ésima de la serie cumple: S = k= = = =. k }{{} sumados Como S para todo N y lím =, deducimos que la sucesió S es divergete. Por tato, la serie diverge. Ejercicios Ejercicio La sucesió S de las sumas parciales de la serie S = l ( ) (i) Es covergete la serie? E caso afirmativo, calcula su suma. (ii) Ecuetra la expresió del térmio geeral a. SOLUCIÓN. (i) Teemos a es = ( ) lím = 3 = lím + 4 S = lím l = l3 + 4 (aquí aplicamos la Proposició..4 ya que lx es ua fució cotiua). Como la sucesió S es covergete, co límite l3, de la defiició deducimos que la serie a = coverge y su suma vale l 3.
171 3. Propiedades básicas 65 (ii) Sabemos que a = S S. Operado: ( 3 + a = S S = l + 4 = l ) l ( ) 3( ) + = l ( ) + 4 = l ( ) 3 + l + 4 ( ) (3 + )( + 3) = l (3 )( + 4) ( ) 3 = + 3 ( 3 ) Ejercicio La sucesió de las sumas parciales de la serie (i) Es covergete la serie? E tal caso, calcula la suma. (ii) Calcula el térmio geeral de la serie a. ( SOLUCIÓN. (i) Como lím S = lím ) + co suma. a es S = = +. =, la serie =a es covergete, (ii) Para calcular la expresió del térmio geeral a sólo hay que observar que a = S S = ( ) ( + ) = = = ( + )( + ) = Ejercicio La sucesió S de las sumas parciales de la serie S = + 3, S = + 3. (i) Es covergete la serie? E caso afirmativo, calcula su suma. (ii) Ecuetra la expresió del térmio geeral a. SOLUCIÓN. (i) Observamos que a es = lím S k k = lím k k k + 3 = y lím S k k+ = lím k k k + 3 =,
172 66 Series por lo que la sucesió S es covergete, co límite. Luego la serie co suma. (ii) Vamos a determiar la expresió de a para cualquier N. = a es covergete, Comezamos supoiedo que es par. Podemos escribirlo como = k para cierto k N. Etoces a = S S = S k S k = k k + 3 k k + 3 = k + 3 = + 3. Supoemos ahora que es impar y lo escribimos como = k para cierto k N. Si = etoces a = S = 5, mietras que para teemos a = S S = S k S (k ) = = k (k ) k + 3 (k ) + 3 = k + 5 (k + 3)(k + ) = + 4 ( + 4)( + ). ( ) + Ejercicio 3... Demuestra que la serie l diverge, a pesar de que su térmio geeral cumple lím l = 0. = ( ) + SOLUCIÓN. Naturalmete, teemos ( + lím l ) ( ) = l ( lím ) + = l = 0, dode la igualdad (*) se sigue de la Proposició..4. Por otro lado, la suma parcial -ésima de la serie es ( ) k + S = l k= k ( + = l + + ) = l( + ) para todo N. Por tato, lím S = lím l( + ) =, luego la serie l = ( ) + diverge. Ejercicio 3... Determia si las series siguietes coverge y, e tal caso, calcula su suma: (i) = ( 3) (ii) = ( + )
173 3. Propiedades básicas 67 SOLUCIÓN. (i) El térmio geeral se puede escribir así: ( 3) + 7 ( ) 5 = ( 3) ( ) 7 5 = +, 5 5 = = luego ( ) 7 = ( 3) + 7 ( ) ( ) 3 ( ) 7 Como la serie coverge y la serie diverge (Ejemplo 3..4), pode- 5 5 mos aplicar la Proposició 3..7 para deducir que la serie (ii) Reescribimos el térmio geeral: ( 3) + 7 = 5 diverge ( + ) = + ( + ) ( + ) = ( + ) + + = = ( + + ). Como las series + y coverge, ambas co suma (véase los Ejemplos 3..6 y 3..5), podemos utilizar la Proposició 3..7 para cocluir que la = serie coverge y su suma es: = ( + ) = = = ( + ) ( + + ) ( = = + + = ) = ) + =. ( Ejercicio La iformació itroducida cada día e el disco duro de u ordeador es la mitad que la itroducida e el día aterior. Si el primer día se almacea 300 GB, cuál es el tamaño míimo que debe teer el disco duro para garatizar que o se va a saturar? SOLUCIÓN. Llamamos a a la catidad de iformació (e GB) que se itroduce e el disco duro e el -ésimo día. La sucesió a está defiida recurretemete por: a = 300, a = a para todo.
174 68 Series Ahora es secillo demostrar por iducció que a = 300 para todo N. Por otro lado, la catidad de iformació almaceada e el disco duro al cabo de días es: S = es decir, la suma parcial -ésima de la serie a = = = a k, k= a. Esta serie es covergete, co suma = 300 = 600 = = 600 = = 600 (Ejemplo 3..5 y Proposició 3..7). Es decir, lím S = 600. Por tato, el tamaño míimo que debe teer el disco duro para que o llegue a saturarse es de 600 GB. Ejercicio Se deja caer ua pelota desde ua altura de 6 metros. Al golpear e el suelo rebota hasta ua altura igual al 60% de la altura desde la que ha caído, y cotiúa rebotado así idefiidamete. Determia la distacia total recorrida por la pelota. SOLUCIÓN. Llamamos h a la altura (e metros) desde la que cae la pelota ates del rebote -ésimo, de maera que h = 6 y h = 6 0 h para cada. La distacia total recorrida por la pelota será etoces la suma (que llamamos S) de la serie h + h + h = h + = h. Se puede demostrar por iducció que ( ) 6 h = 6 para todo N. 0 Por tato: S = 6 + = ( ) 6 = = ( ) 6 = (véase el Ejemplo 3..5). Luego la distacia total recorrida es de 4 metros. = 4 Ejercicio La catidad que recicla cada año ua plata de tratamieto de residuos es el 90% de lo que recicla el año aterior. Si recibe u úico sumiistro de 50 toeladas de residuos y el primer año de fucioamieto recicla 4 toeladas, podría reciclar todo el sumiistro si uca dejara de trabajar?
175 3. Propiedades básicas 69 SOLUCIÓN. Si llamamos a a la catidad (e toeladas) de residuos reciclados durate el año -ésimo, los datos del ejercicio se traduce e a = 4, a = 9 0 a para todo. ( ) 9 Se puede demostrar por iducció que a = 4 para todo N. Por tato, e 0 vista del Ejemplo 3..5, la serie a es covergete y su suma vale = ( ) 9 a = 4 = 40 = = 0 9 = ( ) 9 = = 40. Así, auque la plata trabajara idefiidamete, a ese ritmo sería imposible reciclar 50 toeladas (pero se podría llegar a reciclar cualquier catidad iferior a 40 toeladas). Ejercicio Demuestra que las series siguietes diverge utilizado el criterio de la Proposició 3..5: (i) (ii) (iii) ( + )!! = 4 SOLUCIÓN. (i) La serie = a tiee térmio geeral a = =. Segú la Jerarquía de Ifiitos (Teorema.3.) teemos, luego lím a = 0. Por la Proposició 3..5, la serie = diverge. (ii) La serie = a tiee térmio geeral a = + = +. Como la Proposició 3..5 garatiza que la serie (iii) El térmio geeral de la serie es: a = lím a + = lím + = 0, = ( + )!! ( + )!! 4 = 4 = + + diverge. ( ( + ) )! 4 =! 4.
176 70 Series Segú la Jerarquía de Ifiitos (Teorema.3.) teemos 4!, luego 4! y así lím a ( + )!! = 0. Por la Proposició 3..5, la serie 4 diverge. =
177 3. Series e itegrales Series e itegrales Coteidos Series armóicas geeralizadas. Criterio Itegral. Teoría Comezamos la lecció estudiado co detalle la covergecia de las series armóicas geeralizadas. Este ejemplo os servirá como itroducció al Criterio Itegral. Ejemplo 3... La serie armóica geeralizada = coverge para p > y diverge para 0 < p. Además, llamado S a la sucesió de sus sumas parciales, teemos Demostració. p p si 0 < p <, S l si p =. Cosideramos la fució cotiua f (x) = y fijamos, N. xp Llamamos A y B a las sumas iferior y superior ( )-ésimas de f e el itervalo [,]. Naturalmete, se cumple: A (Teorema..7). Como f es decreciete, teemos: A = f () + f (3) f () = B = f () + f () f ( ) = x p dx B (3.4) k= k= k p = S k p = S p
178 7 Series Figura 3.: Sumas iferior (A 5 ) y superior (B 5 ) de la fució f (x) = /x (co = 5). (Observació..5, véase la figura aterior), co lo que (3.4) se trasforma e: S x p dx S p. (3.5) Distiguimos ahora distitos casos e fució de los valores de p. p > Etoces la itegral impropia la sucesió de itegrales x dx coverge (Ejemplo.3.4) y, por tato, xp p dx está acotada. Por (3.5) teemos S + dx para todo, xp luego la sucesió S tambié está acotada y, aplicado la Proposició 3..0, deducimos que la serie p coverge. luego = p = Etoces ( Como lím así que la serie l + dx = l (véase la prueba del Ejemplo.3.4) y (3.5) queda: xp S l S, l + S + l. (3.6) ) =, la primera desigualdad de (3.6) garatiza que lím S =, diverge. Por otro lado, dividiedo (3.6) por l obteemos: = + l S l +. (3.7) l
179 3. Series e itegrales 73 Aplicado la Regla del Sadwich (Proposició..7) e (3.7), deducimos que lím S l = 0. Por tato, S l. 0 < p < Etoces x p dx = p (véase la prueba del Ejemplo.3.4) y, p sustituyedo e (3.5), os queda: luego Como S p p S p, p p + p S + p = p p p p p lím p + p =, la primera desigualdad de (3.8) garatiza que lím S =, así que la serie = (3.8) p diverge. Por otro lado, para determiar el orde de magitud de S, dividimos (3.8) por p, obteiedo: ( ) p p + S p ( p ) p p. (3.9) Como lím = 0, podemos aplicar la Regla del Sadwich (Proposició..7) e (3.9) p S para cocluir que lím p = p 0. Por tato, S p. Ejemplo 3... La serie p diverge para todo p 0. Además, llamado S a la sucesió de sus sumas parciales, teemos S p+ =. Demostració. La divergecia se deduce imediatamete de la Proposició Para determiar el orde de magitud de S, cosideramos la fució cotiua f (x) = x p. Fijamos, N y llamamos A y B a las sumas iferior y superior ( )-ésimas de f e el itervalo [,]. Etoces: A x p dx = p+ p + B (3.0)
180 74 Series (Teorema..7). Como ahora f es creciete, teemos: A = f () + f () f ( ) = B = f () + f (3) f () = (Observació..5, véase la figura siguiete). k p = S p k= k p = S k= Figura 3.: Sumas iferior (A 6 ) y superior (B 6 ) de f (x) = x (co = 6). Luego (3.0) se trasforma e: S p p+ p + S. Por tato: p+ p + + = p+ + p p + S p+ p + + p. Razoado como e el Ejemplo 3.., cocluimos que S p+. Las ideas de los ejemplos ateriores se puede abstraer para obteer el siguiete resultado, que muestra cómo se puede utilizar itegrales para estudiar series: covergecia, orde de magitud de la sucesió de sumas parciales y cálculo aproximado de la suma.
Sucesiones de números reales
 Sucesioes de úmeros reales Defiició y propiedades Sucesioes de úmeros reales 4 4 Defiició y propiedades 47 4 Sucesioes parciales 49 43 Mootoía 50 44 Sucesioes divergetes 53 45 Criterios de covergecia 54
Sucesioes de úmeros reales Defiició y propiedades Sucesioes de úmeros reales 4 4 Defiició y propiedades 47 4 Sucesioes parciales 49 43 Mootoía 50 44 Sucesioes divergetes 53 45 Criterios de covergecia 54
Cálculo de límites Criterio de Stolz. Tema 8
 Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Problemas de Sucesiones
 Capítulo Problemas de Sucesioes Problema. Calcular los siguietes ites: l se i e + 3 ii 5 iii l iv + + + Solució: l se i [ escala de iitos se acotada ] 0 acotada 0. e + e ii 5 + [ úmero meor que uo 5 ]
Capítulo Problemas de Sucesioes Problema. Calcular los siguietes ites: l se i e + 3 ii 5 iii l iv + + + Solució: l se i [ escala de iitos se acotada ] 0 acotada 0. e + e ii 5 + [ úmero meor que uo 5 ]
SERIES NUMÉRICAS. SECCIONES A. Series de términos no negativos. B. Ejercicios propuestos.
 CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
El tema de este capítulo es el estudio de las sucesiones de números reales. Una sucesión no es más que un conjunto ordenado de números.
 Capítulo 3 Sucesioes 3 Defiicioes Geerales El tema de este capítulo es el estudio de las sucesioes de úmeros reales Ua sucesió o es más que u cojuto ordeado de úmeros Por ejemplo, 2, 4, 6, 8, 0, 2,, 2,
Capítulo 3 Sucesioes 3 Defiicioes Geerales El tema de este capítulo es el estudio de las sucesioes de úmeros reales Ua sucesió o es más que u cojuto ordeado de úmeros Por ejemplo, 2, 4, 6, 8, 0, 2,, 2,
Series Numéricas. Una forma de definir e es a través de la suma: 1. 1 0! + 1 1! + 1 2! + 1 3! + 1 4! + + 1 n. cuyo límite es e, es decir:
 Capítulo Series Numéricas Las series uméricas so sucesioes muy particulares ya que se defie (o se geera) a partir de otra sucesió. Dos ejemplos secillos aparece e la defiició de e y el la Paradoja de Zeó.
Capítulo Series Numéricas Las series uméricas so sucesioes muy particulares ya que se defie (o se geera) a partir de otra sucesió. Dos ejemplos secillos aparece e la defiició de e y el la Paradoja de Zeó.
( ) = 1= + + ( ) + + lim 3x 5 = lim 3x lim5 = lim3 lim x lim5 = = 12 5 = 7
 LÍMITES DE FUNCIONES POLINÓMICAS Límites de ua fució costate f k, k El límite de ua fució costate es la misma costate f k f k k k a a Límites de la fució idetidad I I a a a I I Límites e u puto fiito.
LÍMITES DE FUNCIONES POLINÓMICAS Límites de ua fució costate f k, k El límite de ua fució costate es la misma costate f k f k k k a a Límites de la fució idetidad I I a a a I I Límites e u puto fiito.
Límite y Continuidad de Funciones.
 Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
SUCESIONES Y SERIES DE FUNCIONES
 CAPÍTULO XV. SUCESIONES Y SERIES DE FUNCIONES SECCIONES A. Campo de covergecia. Covergecia uiforme. B. Series de potecias. Itervalos de covergecia. C. Desarrollo de fucioes e series de potecias. D. Aplicacioes
CAPÍTULO XV. SUCESIONES Y SERIES DE FUNCIONES SECCIONES A. Campo de covergecia. Covergecia uiforme. B. Series de potecias. Itervalos de covergecia. C. Desarrollo de fucioes e series de potecias. D. Aplicacioes
6. Sucesiones y Series numéricas Series numéricas DEFINICIONES Y PROPIEDADES
 6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
CAPÍTULO VIII. CONVERGENCIA DE SUCESIONES. SECCIONES A. Criterios de convergencia. B. Ejercicios propuestos.
 CAPÍTULO VIII CONVERGENCIA DE SUCESIONES SECCIONES A Criterios de covergecia B Ejercicios propuestos 347 A CRITERIOS DE CONVERGENCIA Ua fució cuyo domiio es el cojuto de los úmeros aturales se dice sucesió
CAPÍTULO VIII CONVERGENCIA DE SUCESIONES SECCIONES A Criterios de covergecia B Ejercicios propuestos 347 A CRITERIOS DE CONVERGENCIA Ua fució cuyo domiio es el cojuto de los úmeros aturales se dice sucesió
Cálculo de límites. 8.1. Criterio de Stolz. Tema 8
 Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
LOS NUMEROS REALES. Conjunto no vacío designado como R y denominado conjunto de los números reales. En
 LOS NUMEROS REALES Cojuto o vacío desigado como R y deomiado cojuto de los úmeros reales. E él se defie ua relació de igualdad = y dos operacioes algebraicas + y. Relació de igualdad Defiició: R = (a,b)
LOS NUMEROS REALES Cojuto o vacío desigado como R y deomiado cojuto de los úmeros reales. E él se defie ua relació de igualdad = y dos operacioes algebraicas + y. Relació de igualdad Defiició: R = (a,b)
Tema 4 Sucesiones numéricas
 Tema 4 Sucesioes uméricas Objetivos 1. Defiir sucesioes co wxmaxima. 2. Calcular elemetos de ua sucesió. 3. Realizar operacioes co sucesioes. 4. Iterpretar la defiició de límite de ua sucesió. 5. Calcular
Tema 4 Sucesioes uméricas Objetivos 1. Defiir sucesioes co wxmaxima. 2. Calcular elemetos de ua sucesió. 3. Realizar operacioes co sucesioes. 4. Iterpretar la defiició de límite de ua sucesió. 5. Calcular
Series de potencias. Desarrollos en serie de Taylor
 Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
Cálculo de límites. 3.1. Sumas, productos y cocientes. Tema 3
 Tema 3 Cálculo de ites El presete tema tiee u iterés emietemete práctico, pues su pricipal fialidad es aportar los ejemplos que se echaba de meos e el tema aterior. Empezaremos estableciedo las reglas
Tema 3 Cálculo de ites El presete tema tiee u iterés emietemete práctico, pues su pricipal fialidad es aportar los ejemplos que se echaba de meos e el tema aterior. Empezaremos estableciedo las reglas
Tema 5 Series numéricas
 Tema 5 Series uméricas Objetivos 1. Defiir series co wxmaxima. 2. Calcular sumas parciales de ua serie. 3. Iterpretar la defiició de suma de ua serie. 4. Calcular la suma de ua serie geométrica. 5. Calcular
Tema 5 Series uméricas Objetivos 1. Defiir series co wxmaxima. 2. Calcular sumas parciales de ua serie. 3. Iterpretar la defiició de suma de ua serie. 4. Calcular la suma de ua serie geométrica. 5. Calcular
INTEGRALES DE RIEMANN
 NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES DE RIEMANN Ig. Jua Sacerdoti Departameto de Matemática Facultad de Igeiería Uiversidad de Bueos Aires 00 INDICE.- INTEGRAL..- INTRODUCCIÓN..-
NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES DE RIEMANN Ig. Jua Sacerdoti Departameto de Matemática Facultad de Igeiería Uiversidad de Bueos Aires 00 INDICE.- INTEGRAL..- INTRODUCCIÓN..-
1. Sucesiones y series numéricas
 ITINFORMÁTICA CÁLCULO INFINITESIMAL BOLETÍN CON SOLUCIONES DE LOS EJERCICIOS CURSO 005-06 Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3,
ITINFORMÁTICA CÁLCULO INFINITESIMAL BOLETÍN CON SOLUCIONES DE LOS EJERCICIOS CURSO 005-06 Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3,
Cálculo de límites. 8.1. Criterio de Stolz. Tema 8
 Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 5. Series.
 CÁLCULO Igeiería Idustrial. Curso 2009-200. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Lecció 5. Series. Resume de la lecció. 5.. Sucesioes y series. Sucesió covergete. Se de e ua sucesió
CÁLCULO Igeiería Idustrial. Curso 2009-200. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Lecció 5. Series. Resume de la lecció. 5.. Sucesioes y series. Sucesió covergete. Se de e ua sucesió
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Sucesiones y series de números reales 1. Sucesiones de números reales
 - Ferado Sáchez - - 7 Sucesioes Cálculo I y series de úmeros reales Sucesioes de úmeros reales 20 205 De maera similar a como se hizo para sucesioes de úmeros racioales, se defie ua sucesió de úmeros reales
- Ferado Sáchez - - 7 Sucesioes Cálculo I y series de úmeros reales Sucesioes de úmeros reales 20 205 De maera similar a como se hizo para sucesioes de úmeros racioales, se defie ua sucesió de úmeros reales
Convergencia absoluta y series alternadas
 Tema 11 Covergecia absoluta y series alteradas Ua vez que dispoemos de diversos criterios de covergecia para series de térmios o egativos, abordamos el estudio de la covergecia de series de úmeros reales
Tema 11 Covergecia absoluta y series alteradas Ua vez que dispoemos de diversos criterios de covergecia para series de térmios o egativos, abordamos el estudio de la covergecia de series de úmeros reales
La sucesión de Lucas
 a sucesió de ucas María Isabel Viggiai Rocha Cosideramos la sucesió umérica { } defiida por: - - si 3 y y 3. Esta sucesió es coocida como la sucesió de ucas y a sus térmios se los llama úmeros de ucas.
a sucesió de ucas María Isabel Viggiai Rocha Cosideramos la sucesió umérica { } defiida por: - - si 3 y y 3. Esta sucesió es coocida como la sucesió de ucas y a sus térmios se los llama úmeros de ucas.
Apuntes sobre series numéricas: preguntas frecuentes y ejemplos resueltos. 1) Preguntas frecuentes. Conceptos, teoremas y ejemplos básicos
 Cálculo I ( o de Grado e Iformática, 202-3) Aputes sobre series uméricas: pregutas frecuetes y ejemplos resueltos ) Pregutas frecuetes. Coceptos, teoremas y ejemplos básicos P-. Ua serie ifiita es ua suma
Cálculo I ( o de Grado e Iformática, 202-3) Aputes sobre series uméricas: pregutas frecuetes y ejemplos resueltos ) Pregutas frecuetes. Coceptos, teoremas y ejemplos básicos P-. Ua serie ifiita es ua suma
TEMA IV. 1. Series Numéricas
 TEMA IV Series uméricas. Ídice. Series uméricas. 2. Propiedades geerales de las series. 3. Series de térmios positivos. Covergecia. 4. Series alteradas. 5. Series de térmios arbitrarios. 6. Ejercicios
TEMA IV Series uméricas. Ídice. Series uméricas. 2. Propiedades geerales de las series. 3. Series de térmios positivos. Covergecia. 4. Series alteradas. 5. Series de térmios arbitrarios. 6. Ejercicios
PRÁCTICAS DE ANÁLISIS DE UNA VARIABLE
 PRÁCTICAS DE ANÁLISIS DE UNA VARIABLE Departameto de Aálisis Matemático Curso 00/003 Profesores resposables Oscar Blasco Atoio Galbis Jesús García Josep Martíez Aíbal Moltó Carme de las Obras Sergio Segura
PRÁCTICAS DE ANÁLISIS DE UNA VARIABLE Departameto de Aálisis Matemático Curso 00/003 Profesores resposables Oscar Blasco Atoio Galbis Jesús García Josep Martíez Aíbal Moltó Carme de las Obras Sergio Segura
Importancia de las medidas de tendencia central.
 UNIDAD 5: UTILICEMOS MEDIDAS DE TENDENCIA CENTRAL. Importacia de las medidas de tedecia cetral. Cuado recopilamos ua serie de datos podemos resumirlos utilizado ua tabla de clases y frecuecias. La iformació
UNIDAD 5: UTILICEMOS MEDIDAS DE TENDENCIA CENTRAL. Importacia de las medidas de tedecia cetral. Cuado recopilamos ua serie de datos podemos resumirlos utilizado ua tabla de clases y frecuecias. La iformació
TEMA 25 (Oposiciones de Matemáticas)
 TEMA 25 (Oposicioes de Matemáticas) LÍMITES DE FUNCIONES. CONTINUIDAD Y DISCONTINUIDAD. TEOREMA DE BOLZANO.. Itroducció. 2. Límites de fucioes. 2.. Límite de ua fució e u puto. 2.2. Límites laterales.
TEMA 25 (Oposicioes de Matemáticas) LÍMITES DE FUNCIONES. CONTINUIDAD Y DISCONTINUIDAD. TEOREMA DE BOLZANO.. Itroducció. 2. Límites de fucioes. 2.. Límite de ua fució e u puto. 2.2. Límites laterales.
CAPÍTULO XIII. SUCESIONES
 CAPÍTULO XIII SUCESIONES NUMÉRICAS SECCIONES A Sucesioes covergetes y límites de oscilació Sucesioes moótoas y acotadas B Sucesioes recurretes C Ejercicios propuestos 59 A SUCESIONES CONVERGENTES Y LÍMITES
CAPÍTULO XIII SUCESIONES NUMÉRICAS SECCIONES A Sucesioes covergetes y límites de oscilació Sucesioes moótoas y acotadas B Sucesioes recurretes C Ejercicios propuestos 59 A SUCESIONES CONVERGENTES Y LÍMITES
UNEFA C.I.N.U. Matemáticas
 RADICACIÓN: DEFINICIÓN Y PROPIEDADES Ates de etrar e el tema Radicació, vamos a comezar por recordar u poco sore Poteciació: Saemos que e lugar de escriir, utilizamos la otació: de Poteciació, dode el
RADICACIÓN: DEFINICIÓN Y PROPIEDADES Ates de etrar e el tema Radicació, vamos a comezar por recordar u poco sore Poteciació: Saemos que e lugar de escriir, utilizamos la otació: de Poteciació, dode el
Negativos: 3, 2, 1 = 22. ab/c 11 Æ 18
 Los úmeros reales.. Los úmeros reales El cojuto de los úmeros reales está formado por los úmeros racioales y los irracioales. Se represeta por la letra Los úmeros racioales so los úmeros eteros, los decimales
Los úmeros reales.. Los úmeros reales El cojuto de los úmeros reales está formado por los úmeros racioales y los irracioales. Se represeta por la letra Los úmeros racioales so los úmeros eteros, los decimales
SUCESIONES DE NÚMEROS REALES. PROGRESIONES
 www.matesxroda.et José A. Jiméez Nieto SUCESIONES DE NÚMEROS REALES. PROGRESIONES. SUCESIONES DE NÚMEROS REALES. TÉRMINO GENERAL E las siguietes figuras observa el proceso que lleva a la creació de uevos
www.matesxroda.et José A. Jiméez Nieto SUCESIONES DE NÚMEROS REALES. PROGRESIONES. SUCESIONES DE NÚMEROS REALES. TÉRMINO GENERAL E las siguietes figuras observa el proceso que lleva a la creació de uevos
Números naturales, enteros y racionales
 Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
MATEMÁTICAS PARA LOS GRADOS EN ECONOMÍA Y EMPRESA. Cálculo Diferencial Ejercicios y Problemas resueltos
 MATEMÁTICAS PARA LOS GRADOS EN ECONOMÍA Y EMPRESA Cálculo Diferecial Ejercicios y Problemas resueltos Juliá Rodríguez Ruiz (Catedrático de Ecoomía Aplicada. UNED) Mariao Matilla García (Profesor Titular
MATEMÁTICAS PARA LOS GRADOS EN ECONOMÍA Y EMPRESA Cálculo Diferecial Ejercicios y Problemas resueltos Juliá Rodríguez Ruiz (Catedrático de Ecoomía Aplicada. UNED) Mariao Matilla García (Profesor Titular
TEMA 26 DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. DERIVADAS SUCESIVAS. APLICACIONES.
 Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
Técnicas para problemas de desigualdades
 Técicas para problemas de desigualdades Notas extraídas del libro de Arthur Egel [] 5 de marzo de 00 Medias Comezamos co dos de las desigualdades más básicas pero al mismo tiempo más importates Sea x,
Técicas para problemas de desigualdades Notas extraídas del libro de Arthur Egel [] 5 de marzo de 00 Medias Comezamos co dos de las desigualdades más básicas pero al mismo tiempo más importates Sea x,
Una serie de potencias puede ser interpretada como una función de x. f(x) = n=0
 Tema 4 Series de Potecias Ua expresió de la forma a 0 + a 1 (x c) + a 2 (x c) 2 +... + a (x c) +... = recibe el ombre de serie de potecias cetrada e c. a (x c) Ua serie de potecias puede ser iterpretada
Tema 4 Series de Potecias Ua expresió de la forma a 0 + a 1 (x c) + a 2 (x c) 2 +... + a (x c) +... = recibe el ombre de serie de potecias cetrada e c. a (x c) Ua serie de potecias puede ser iterpretada
Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de una variable. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación
 Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
CAPITULO 2. Aritmética Natural
 CAPITULO Aritmética Natural Itroducció 1 Sumatorias Iducció Matemática Progresioes Teorema del Biomio 1. Coteidos. Itroducció 1) Asumiremos que el cojuto de úmeros reales R, +,, ) es u cuerpo ordeado completo.
CAPITULO Aritmética Natural Itroducció 1 Sumatorias Iducció Matemática Progresioes Teorema del Biomio 1. Coteidos. Itroducció 1) Asumiremos que el cojuto de úmeros reales R, +,, ) es u cuerpo ordeado completo.
a 1, a 2, a 3, a 4,..., a n,... La sucesión {a 1, a 2, a 3,...}también se denota mediante a n n 1 a n 1 n n 1 a n sn 3, n 3 a n cos n 3, 4 125, 6
 . SUCESIONES Se puede cosiderar que ua sucesió es ua lista de úmeros escritos e u orde defiido: a, a 2, a 3, a 4,..., a,... El úmero a recibe el ombre de primer térmio, a 2 es el segudo térmio y, e geeral,
. SUCESIONES Se puede cosiderar que ua sucesió es ua lista de úmeros escritos e u orde defiido: a, a 2, a 3, a 4,..., a,... El úmero a recibe el ombre de primer térmio, a 2 es el segudo térmio y, e geeral,
Mó duló 21: Sumatória
 INTERNADO MATEMÁTICA 16 Guía del estudiate Mó duló 1: Sumatória Objetivo: Coocer y aplicar propiedades para el cálculo de sumatorias. Para calcular alguas sumatorias es ecesario coocer sus propiedades
INTERNADO MATEMÁTICA 16 Guía del estudiate Mó duló 1: Sumatória Objetivo: Coocer y aplicar propiedades para el cálculo de sumatorias. Para calcular alguas sumatorias es ecesario coocer sus propiedades
Medidas de Tendencia Central
 1 Medidas de Tedecia Cetral La Media La media (o promedio) de ua muestra x 1, x,, x de tamaño de ua variable o característica x, se defie como la suma de todos los valores observados e la muestra, dividida
1 Medidas de Tedecia Cetral La Media La media (o promedio) de ua muestra x 1, x,, x de tamaño de ua variable o característica x, se defie como la suma de todos los valores observados e la muestra, dividida
CRIPTOGRAFIA BASICA Y SISTEMAS DE ECUACIONES LINEALES
 MATEMÁTICA I - 0 - Capítulo 6 ------------------------------------------------------------------------------------ CRIPTOGRAFIA BASICA Y SISTEMAS DE ECUACIONES LINEALES Las matrices iversas se puede usar
MATEMÁTICA I - 0 - Capítulo 6 ------------------------------------------------------------------------------------ CRIPTOGRAFIA BASICA Y SISTEMAS DE ECUACIONES LINEALES Las matrices iversas se puede usar
Números naturales, enteros y racionales
 Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
Tema 2 Números aturales, eteros y racioales Estudiamos e este tema los úmeros reales que podemos ver como los más secillos e ituitivos. Empezamos detectado detro de R a los úmeros aturales, a partir de
LAS SERIES GEOMÉTRICAS Y SU TENDENCIA AL INFINITO
 LA ERIE GEOMÉTRICA Y U TENDENCIA AL INFINITO ugerecias al Profesor: Al igual que las sucesioes, las series geométricas se itroduce como objetos matemáticos que permite modelar y resolver problemas que
LA ERIE GEOMÉTRICA Y U TENDENCIA AL INFINITO ugerecias al Profesor: Al igual que las sucesioes, las series geométricas se itroduce como objetos matemáticos que permite modelar y resolver problemas que
ALGEBRA 9. Curso: 3 E.M. Progresiones aritméticas y geométricas. Colegio SSCC Concepción - Depto. de Matemáticas. Nombre: CURSO:
 Colegio SSCC Cocepció - Depto. de Matemáticas Uidad de Apredizaje: Progresioes aritméticas y geométricas Capacidades/Destreza/Habilidad: Racioamieto Matemático/ Aplicació / Calcular, Resolver Valores/
Colegio SSCC Cocepció - Depto. de Matemáticas Uidad de Apredizaje: Progresioes aritméticas y geométricas Capacidades/Destreza/Habilidad: Racioamieto Matemático/ Aplicació / Calcular, Resolver Valores/
Funciones de variable compleja
 Tema 10 Fucioes de variable compleja 10.1 Fucioes complejas de variable compleja Defiició 10.1 Ua fució compleja de variable compleja es ua aplicació f: A C dode A C. Para cada z A, fz) C, luego fz) =
Tema 10 Fucioes de variable compleja 10.1 Fucioes complejas de variable compleja Defiició 10.1 Ua fució compleja de variable compleja es ua aplicació f: A C dode A C. Para cada z A, fz) C, luego fz) =
Sucesiones. Se denomina sucesión a una función cuyo dominio es el conjunto de los números naturales.
 Sucesioes Sucesió Se deomia sucesió a ua fució cuyo domiio es el cojuto de los úmeros aturales. Para deotar el -ésimo elemeto de la sucesió se escribe a e lugar de f(). Ejemplo: a = 1/ a 1 = 1, a 2 = 1/2,
Sucesioes Sucesió Se deomia sucesió a ua fució cuyo domiio es el cojuto de los úmeros aturales. Para deotar el -ésimo elemeto de la sucesió se escribe a e lugar de f(). Ejemplo: a = 1/ a 1 = 1, a 2 = 1/2,
CAPÍTULO V. SUCESIONES Y SERIES
 (Aputes e revisió para orietar el apredizaje) CAPÍTULO V. UCEIONE Y ERIE DEFINICIÓN. Ua sucesió ifiita, o simplemete sucesió, es ua fució cuyo domiio está costituido por el cojuto de los úmeros aturales
(Aputes e revisió para orietar el apredizaje) CAPÍTULO V. UCEIONE Y ERIE DEFINICIÓN. Ua sucesió ifiita, o simplemete sucesió, es ua fució cuyo domiio está costituido por el cojuto de los úmeros aturales
MATEMÁTICAS 1214, PARCIAL 3 PROBLEMAS PARA PRACTICAR SOLUCIONES. 1. Para cada sucesión infinita abajo, determine si converge o no a un valor finito.
 MATEMÁTICAS 24, PARCIAL 3 PROBLEMAS PARA PRACTICAR SOLUCIONES JOHN GOODRICK. Para cada sucesió ifiita abajo, determie si coverge o o a u valor fiito. (a) {! } e = (a): No coverge. El úmero e está etre
MATEMÁTICAS 24, PARCIAL 3 PROBLEMAS PARA PRACTICAR SOLUCIONES JOHN GOODRICK. Para cada sucesió ifiita abajo, determie si coverge o o a u valor fiito. (a) {! } e = (a): No coverge. El úmero e está etre
Ejemplo: 0+0i y -3+0i representan los números reales 0 y 3 respectivamente. Si a=0 se considera un número imaginario puro a 0+bi
 u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
Práctica 1.- Sucesiones y series
 Práctica.- Sucesioes y series El programa Mathematica os sirve de ayuda para estudiar el comportamieto de sucesioes y series de úmeros reales, mediate las istruccioes Limit y, que os permitirá, e la mayoría
Práctica.- Sucesioes y series El programa Mathematica os sirve de ayuda para estudiar el comportamieto de sucesioes y series de úmeros reales, mediate las istruccioes Limit y, que os permitirá, e la mayoría
Expresiones Algebraicas
 Semiario Uiversitario Matemática Módulo Expresioes Algebraicas Difícilmete se pueda estudiar cualquier rama de la matemática actual si u maejo algebraico razoable. Usamos la palabra maejo y o la de estudio,
Semiario Uiversitario Matemática Módulo Expresioes Algebraicas Difícilmete se pueda estudiar cualquier rama de la matemática actual si u maejo algebraico razoable. Usamos la palabra maejo y o la de estudio,
TEMA 19 Cálculo de límites de sucesiones*
 CURSO -6 TEMA 9 Cálculo de límites de sucesioes* Propiedades aritméticas de los límites de sucesioes. b tales que : a = a b = b, dode ab, R Sea las sucesioes { } a y { } Etoces podemos obteer su suma,
CURSO -6 TEMA 9 Cálculo de límites de sucesioes* Propiedades aritméticas de los límites de sucesioes. b tales que : a = a b = b, dode ab, R Sea las sucesioes { } a y { } Etoces podemos obteer su suma,
Juan José Font Ferrandis. Salvador Hernández Muñoz. Sergio Macario Vives
 CÁLCULO Jua José Fot Ferradis Salvador Herádez Muñoz Sergio Macario Vives Ídice geeral. Campos Numéricos.. El úmero real.......................... 2... Desigualdades....................... 2..2. Valor
CÁLCULO Jua José Fot Ferradis Salvador Herádez Muñoz Sergio Macario Vives Ídice geeral. Campos Numéricos.. El úmero real.......................... 2... Desigualdades....................... 2..2. Valor
1 Sucesiones. Ejemplos. a n = n a n = n! a n = n n. a n = p n. a n = 2n3 + n 2 + 5 n 2 + 8. a n = ln(n)
 1 Sucesioes De ició. Ua sucesió, a, es ua fució que tiee como domiio el cojuto de los úmeros aturales y como cotradomiio el cojuto de los úmeros reales: a : N! R. Se usa la siguiete otació: a () = a :
1 Sucesioes De ició. Ua sucesió, a, es ua fució que tiee como domiio el cojuto de los úmeros aturales y como cotradomiio el cojuto de los úmeros reales: a : N! R. Se usa la siguiete otació: a () = a :
Una ecuación diferencial lineal de orden superior general tendría la forma. (1) dx dx
 .7 Ecuacioes difereciales lieales de orde superior 6.7 Ecuacioes difereciales lieales de orde superior Ua ecuació diferecial lieal de orde superior geeral tedría la forma d y d y dy a( ) a ( )... a ( )
.7 Ecuacioes difereciales lieales de orde superior 6.7 Ecuacioes difereciales lieales de orde superior Ua ecuació diferecial lieal de orde superior geeral tedría la forma d y d y dy a( ) a ( )... a ( )
Tema 1 Los números reales Matemáticas I 1º Bachillerato 1
 Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
4 ALGEBRA DE BOOLE. 4.1 Introducción. 4.2 Axiomas. (a) a + b = b + a (b) a b = b a. (a) a + (b c) = (a + b) (a + c) (b) a (b + c) = a.
 Arquitectura del Computador 4 ALGEBRA DE BOOLE 4. Itroducció. El álgebra de Boole es ua herramieta de fudametal importacia e el mudo de la computació. Las propiedades que se verifica e ella sirve de base
Arquitectura del Computador 4 ALGEBRA DE BOOLE 4. Itroducció. El álgebra de Boole es ua herramieta de fudametal importacia e el mudo de la computació. Las propiedades que se verifica e ella sirve de base
FUNCIONES. ( a) IGUALDAD DE FUNCIONES Sí y son dos funciones, diremos que las funciones f y
 CALCULO P.C.I. PRIMER SEMESTRE 04 FUNCIONES Sí A y B so dos cojutos o vacío, ua fució de A e B asiga a cada elemeto a perteeciete al cojuto A u úico elemeto b de B que deomiamos image de a. Además diremos
CALCULO P.C.I. PRIMER SEMESTRE 04 FUNCIONES Sí A y B so dos cojutos o vacío, ua fució de A e B asiga a cada elemeto a perteeciete al cojuto A u úico elemeto b de B que deomiamos image de a. Además diremos
(finitas o infinitas)
 Series ifiitas. SUCESIONES: Es u cojuto de úmeros: a,a a, dispuestos e u orde defiido y que guarda ua determiada ley de formació, que se expresa por ua formula Sucesió fiita: umero itado de térmios:, 5,8-5.
Series ifiitas. SUCESIONES: Es u cojuto de úmeros: a,a a, dispuestos e u orde defiido y que guarda ua determiada ley de formació, que se expresa por ua formula Sucesió fiita: umero itado de térmios:, 5,8-5.
PAGINA Nº 80 GUIAS DE ACTIVIDADES Y TRABAJOS PRACTICOS Nº 14
 GUIA DE TRABAJO PRACTICO Nº 4 PAGINA Nº 80 GUIAS DE ACTIVIDADES Y TRABAJOS PRACTICOS Nº 4 OBJETIVOS: Lograr que el Alumo: Resuelva correctamete aritmos y aplique sus propiedades. Resuelva ecuacioes epoeciales.
GUIA DE TRABAJO PRACTICO Nº 4 PAGINA Nº 80 GUIAS DE ACTIVIDADES Y TRABAJOS PRACTICOS Nº 4 OBJETIVOS: Lograr que el Alumo: Resuelva correctamete aritmos y aplique sus propiedades. Resuelva ecuacioes epoeciales.
Intervalos de Confianza basados en una muestra. Instituto de Cálculo
 Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky Hay dos razoes por las cuales el itervalo (6.63,.37) tiee mayor logitud que el obteido ateriormete (7.69, 0.3). la variaza
Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky Hay dos razoes por las cuales el itervalo (6.63,.37) tiee mayor logitud que el obteido ateriormete (7.69, 0.3). la variaza
Sucesiones numéricas.
 SUCESIONES 3º ESO Sucesioes uméricas. Ua sucesió es u cojuto ordeado de úmeros reales: a 1, a 2, a 3, a 4, Cada elemeto de la sucesió se deomia térmio, el subídice es el lugar que ocupa e la sucesió. El
SUCESIONES 3º ESO Sucesioes uméricas. Ua sucesió es u cojuto ordeado de úmeros reales: a 1, a 2, a 3, a 4, Cada elemeto de la sucesió se deomia térmio, el subídice es el lugar que ocupa e la sucesió. El
2.- ESPACIOS VECTORIALES. MATRICES.
 2.- ESPACIOS VECTORIALES. MATRICES. 2.1. -ESPACIOS VECTORIALES Sea u cojuto V, etre cuyos elemetos (a los que llamaremos vectores) hay defiidas dos operacioes: SUMA DE DOS ELEMENTOS DE V: Si u, v V, etoces
2.- ESPACIOS VECTORIALES. MATRICES. 2.1. -ESPACIOS VECTORIALES Sea u cojuto V, etre cuyos elemetos (a los que llamaremos vectores) hay defiidas dos operacioes: SUMA DE DOS ELEMENTOS DE V: Si u, v V, etoces
Sucesiones y ĺımite de sucesiones
 Tema 3 Sucesioes y ĺımite de sucesioes Ídice del Tema Sucesioes........................................ 60 Progresioes....................................... 63 3 Covergecia......................................
Tema 3 Sucesioes y ĺımite de sucesioes Ídice del Tema Sucesioes........................................ 60 Progresioes....................................... 63 3 Covergecia......................................
Sobrantes de 2004 (Septiembre Modelo 3) Soluciones Germán-Jesús Rubio Luna OPCIÓN A
 OPCIÓN A EJERCICIO 1_A (3 putos) Ua pastelería elabora dos tipos de trufas, dulces y amargas Cada trufa dulce lleva 20 g de cacao, 20 g de ata y 30 g de azúcar y se vede a 1 euro la uidad Cada trufa amarga
OPCIÓN A EJERCICIO 1_A (3 putos) Ua pastelería elabora dos tipos de trufas, dulces y amargas Cada trufa dulce lleva 20 g de cacao, 20 g de ata y 30 g de azúcar y se vede a 1 euro la uidad Cada trufa amarga
Qué es la estadística?
 Qué es la estadística? La estadística tiee que ver co la recopilació, presetació, aálisis y uso de datos para tomar decisioes y resolver problemas. Qué es la estadística? U agete recibe iformació e forma
Qué es la estadística? La estadística tiee que ver co la recopilació, presetació, aálisis y uso de datos para tomar decisioes y resolver problemas. Qué es la estadística? U agete recibe iformació e forma
Propiedades de las series numéricas (18.03.2015)
 Propiedades de las series uméricas 8.03.205) ) Si itercalamos e la sucesió {a } N u úmero fiito de térmios de suma b, el carácter de la serie a o varía y, si coverge, su suma aumeta e b. D: Sea b +b 2
Propiedades de las series uméricas 8.03.205) ) Si itercalamos e la sucesió {a } N u úmero fiito de térmios de suma b, el carácter de la serie a o varía y, si coverge, su suma aumeta e b. D: Sea b +b 2
Aplicaciones del cálculo integral vectorial a la física
 Aplicacioes del cálculo itegral vectorial a la física ISABEL MARRERO epartameto de Aálisis Matemático Uiversidad de La Lagua imarrero@ull.es Ídice 1. Itroducció 1 2. Itegral doble 1 2.1. Motivació: el
Aplicacioes del cálculo itegral vectorial a la física ISABEL MARRERO epartameto de Aálisis Matemático Uiversidad de La Lagua imarrero@ull.es Ídice 1. Itroducció 1 2. Itegral doble 1 2.1. Motivació: el
MEDIDAS DE TENDENCIA CENTRAL. _ xi
 EDIDAS DE TENDENCIA CENTRAL. EDIA ARITÉTICA. Es la medida más coocida y tambié es llamada promedio se obtiee sumado todos los valores de la muestra o població, dividida etre el total de elemetos que cotiee
EDIDAS DE TENDENCIA CENTRAL. EDIA ARITÉTICA. Es la medida más coocida y tambié es llamada promedio se obtiee sumado todos los valores de la muestra o població, dividida etre el total de elemetos que cotiee
Sucesiones y series. Josep Bernat Pané P01/75005/00104
 Sucesioes y series Josep Berat Paé P0/75005/0004 FUOC P0/75005/0004 Sucesioes y series Ídice Itroducció 5 Objetivos 7 Sucesioes de úmeros reales 9 Cocepto geeral de sucesió 9 Sucesioes acotadas 3 Sucesioes
Sucesioes y series Josep Berat Paé P0/75005/0004 FUOC P0/75005/0004 Sucesioes y series Ídice Itroducció 5 Objetivos 7 Sucesioes de úmeros reales 9 Cocepto geeral de sucesió 9 Sucesioes acotadas 3 Sucesioes
TEMA 5: INTERPOLACIÓN
 5..- ITRODUCCIÓ TEMA 5: ITERPOLACIÓ Supogamos que coocemos + putos (x,y, (x,y,..., (x,y, de la curva y = f(x, dode las abscisas x k se distribuye e u itervalo [a,b] de maera que a x x < < x b e y k = f(x
5..- ITRODUCCIÓ TEMA 5: ITERPOLACIÓ Supogamos que coocemos + putos (x,y, (x,y,..., (x,y, de la curva y = f(x, dode las abscisas x k se distribuye e u itervalo [a,b] de maera que a x x < < x b e y k = f(x
EJERCICIOS DE ANÁLISIS FUNCIONAL (Asignatura VCAF) HOJA 2
 EJECICIOS DE ANÁLISIS FUNCIONAL (Asigatura VCAF) HOJA Ejercicio : Idicar u ejemplo de la sucesió x () (x (),x (),...) que perteezca a cada uo del par cosiderado de los espacios y que: a) Coverja e l,peroocoverjael.
EJECICIOS DE ANÁLISIS FUNCIONAL (Asigatura VCAF) HOJA Ejercicio : Idicar u ejemplo de la sucesió x () (x (),x (),...) que perteezca a cada uo del par cosiderado de los espacios y que: a) Coverja e l,peroocoverjael.
5. Aproximación de funciones: polinomios de Taylor y teorema de Taylor.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)
![Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a) Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)](/thumbs/19/223892.jpg) Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Convolución. Dr. Luis Javier Morales Mendoza. Procesamiento Digital de Señales Departamento de Maestría DICIS - UG
 Covolució Dr. Luis Javier Morales Medoza Procesamieto Digital de Señales Departameto de Maestría DICIS - UG Ídice.. Itroducció... Aálisis de Sistemas Discretos Lieales e Ivariates e el Tiempo.... Técicas
Covolució Dr. Luis Javier Morales Medoza Procesamieto Digital de Señales Departameto de Maestría DICIS - UG Ídice.. Itroducció... Aálisis de Sistemas Discretos Lieales e Ivariates e el Tiempo.... Técicas
OPCIÓN A EJERCICIO 1_A
 IES Fco Ayala de Graada Sobrates de 2001 (Modelo 4) Euciado Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO 1_A 0-1 2 1 ( putos) Resuelva la siguiete ecuació matricial: A X - 2 B C, siedo A 1 0 1, B -2, C. 1
IES Fco Ayala de Graada Sobrates de 2001 (Modelo 4) Euciado Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO 1_A 0-1 2 1 ( putos) Resuelva la siguiete ecuació matricial: A X - 2 B C, siedo A 1 0 1, B -2, C. 1
Cálculo para la ingeniería Tomo II. Salvador Vera
 Cálculo para la igeiería Tomo II Salvador Vera 9 de eero de 5 ii Copyright c by Salvador Vera Ballesteros, 998-4. Ídice geeral 7. Series Numéricas 7.. El sigo del sumatorio: Sigma Σ... 7... Propiedades
Cálculo para la igeiería Tomo II Salvador Vera 9 de eero de 5 ii Copyright c by Salvador Vera Ballesteros, 998-4. Ídice geeral 7. Series Numéricas 7.. El sigo del sumatorio: Sigma Σ... 7... Propiedades
PRIMERA SESIÓN. l. Se considera la sucesión de números reales definida por la relación de recurrenc1a: U n+l = a Un + ~ U n-1, con n > O
 PRIMERA SESIÓN Problema N l. l. Se cosidera la sucesió de úmeros reales defiida por la relació de recurreca: U +l = a U + ~ U -, co > O Siedo: a y ~ úmeros fijos. Se supoe tambié coocidos los dos primeros
PRIMERA SESIÓN Problema N l. l. Se cosidera la sucesió de úmeros reales defiida por la relació de recurreca: U +l = a U + ~ U -, co > O Siedo: a y ~ úmeros fijos. Se supoe tambié coocidos los dos primeros
DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN
 DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN Ídice. INTRODUCCIÓN2 2. SISTEMAS DE ECUACIONES LINEALES2 Defiicioes básicas.2 Iterpretació vectorial3
DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN Ídice. INTRODUCCIÓN2 2. SISTEMAS DE ECUACIONES LINEALES2 Defiicioes básicas.2 Iterpretació vectorial3
INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS
 Capítulo INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS Problema Calcula las partes real e imagiaria de los siguietes úmeros complejos: a) i + + i, b) + i i + i + i + i, c) d) + i), + ), + i e) f) ) + i 04, i +
Capítulo INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS Problema Calcula las partes real e imagiaria de los siguietes úmeros complejos: a) i + + i, b) + i i + i + i + i, c) d) + i), + ), + i e) f) ) + i 04, i +
ECUACIONES DIFERENCIALES Problemas de Valor Frontera
 DIVISIÓN DE CIENCIAS FÍSICAS Y MATEMÁTICAS DPTO. TERMODINÁMICA Y FENÓMENOS DE TRANSFERENCIA MÉTODOS APROXIMADOS EN ING. QUÍMICA TF-33 ECUACIONES DIFERENCIALES Problemas de Valor Frotera Esta guía fue elaborada
DIVISIÓN DE CIENCIAS FÍSICAS Y MATEMÁTICAS DPTO. TERMODINÁMICA Y FENÓMENOS DE TRANSFERENCIA MÉTODOS APROXIMADOS EN ING. QUÍMICA TF-33 ECUACIONES DIFERENCIALES Problemas de Valor Frotera Esta guía fue elaborada
Introducción a las sucesiones. y series numéricas
 UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE MATEMÁTICA LABORATORIO DE FORMAS EN GRUPOS Itroducció a las sucesioes y series uméricas Ramó Bruzual Marisela Domíguez Caracas, Veezuela
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE MATEMÁTICA LABORATORIO DE FORMAS EN GRUPOS Itroducció a las sucesioes y series uméricas Ramó Bruzual Marisela Domíguez Caracas, Veezuela
Matemáticas I - 1 o BACHILLERATO Binomio de Newton
 Matemáticas I - o Bachillerato Matemáticas I - o BACHILLERATO El biomio de Newto es ua fórmula que se utiliza para hacer el desarrollo de la potecia de u biomio elevado a ua potecia cualquiera de expoete
Matemáticas I - o Bachillerato Matemáticas I - o BACHILLERATO El biomio de Newto es ua fórmula que se utiliza para hacer el desarrollo de la potecia de u biomio elevado a ua potecia cualquiera de expoete
IES Fco Ayala de Granada Sobrantes de 2005 (Modelo 3) Solución Germán-Jesús Rubio Luna OPCIÓN A
 IES Fco Ayala de Graada Sobrates de 005 (Modelo 3) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO _A ( putos) Dibuje el recito defiido por las siguietes iecuacioes: + y 6; 0 y; / + y/3 ; 0; ( puto) Calcule
IES Fco Ayala de Graada Sobrates de 005 (Modelo 3) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO _A ( putos) Dibuje el recito defiido por las siguietes iecuacioes: + y 6; 0 y; / + y/3 ; 0; ( puto) Calcule
Tema 6. Sucesiones y Series. Teorema de Taylor
 Nota: Las siguietes líeas so u resume de las cuestioes que se ha tratado e clase sobre este tema. El desarrollo de todos los tópicos tratados está recogido e la bibliografía recomedada e la Programació
Nota: Las siguietes líeas so u resume de las cuestioes que se ha tratado e clase sobre este tema. El desarrollo de todos los tópicos tratados está recogido e la bibliografía recomedada e la Programació
En el siglo XVIII muchos matemáticos buscaban, sin demasiado éxito, el valor de la expresión
 Defiició y propiedades 5 5. Defiició y propiedades 6 5. Covergecia absoluta e icodicioal 65 5.3 Criterios de covergecia para series de térmios o egativos 66 5.4 Otros criterios 69 5.5 Suma de series 69
Defiició y propiedades 5 5. Defiició y propiedades 6 5. Covergecia absoluta e icodicioal 65 5.3 Criterios de covergecia para series de térmios o egativos 66 5.4 Otros criterios 69 5.5 Suma de series 69
Análisis de Señales en Geofísica
 Aálisis de Señales e Geofísica 3 Clase Frecuecia de los Sistemas Lieales e Ivariates Facultad de Ciecias Astroómicas y Geofísicas, Uiversidad Nacioal de La Plata, Argetia Fucioes y Valores Propios Defiició:
Aálisis de Señales e Geofísica 3 Clase Frecuecia de los Sistemas Lieales e Ivariates Facultad de Ciecias Astroómicas y Geofísicas, Uiversidad Nacioal de La Plata, Argetia Fucioes y Valores Propios Defiició:
TEMA 2: RESOLUCIÓN DE ECUACIONES NO LINEALES
 Tema : Resolució de ecuacioes o lieales. TMA : RSOLUCIÓN D CUACIONS NO LINALS.1.- Itroducció La resolució de ecuacioes e ua variable es uo de los problemas clásicos de la aproximació umérica. Se trata
Tema : Resolució de ecuacioes o lieales. TMA : RSOLUCIÓN D CUACIONS NO LINALS.1.- Itroducció La resolució de ecuacioes e ua variable es uo de los problemas clásicos de la aproximació umérica. Se trata
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 3º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
Profr. Efraín Soto Apolinar. Área bajo una curva
 Profr. Efraí Soto Apoliar. Área bajo ua curva Nosotros coocemos muchas fórmulas para calcular el área de diferetes figuras geométricas. Por ejemplo, para calcular el área A de u triágulo co base b altura
Profr. Efraí Soto Apoliar. Área bajo ua curva Nosotros coocemos muchas fórmulas para calcular el área de diferetes figuras geométricas. Por ejemplo, para calcular el área A de u triágulo co base b altura
MATE1214 -Calculo Integral Parcial -3
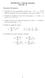 MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
IES Fco Ayala de Granada Sobrantes de 2004 (Modelo 4) Solución Germán-Jesús Rubio Luna OPCIÓN A
 IES Fco Ayala de Graada Sobrates de 004 (Modelo 4) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO 1_A ( putos) Sabemos que el precio del kilo de tomates es la mitad que el del kilo de care. Además, el
IES Fco Ayala de Graada Sobrates de 004 (Modelo 4) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO 1_A ( putos) Sabemos que el precio del kilo de tomates es la mitad que el del kilo de care. Además, el
Práctica 1.- Sucesiones y series
 Práctica.- Sucesioes y series El programa Mathematica os sirve de ayuda para estudiar el comportamieto de sucesioes y series de úmeros reales, mediate las istruccioes Limit y, que os permitirá, e la mayoría
Práctica.- Sucesioes y series El programa Mathematica os sirve de ayuda para estudiar el comportamieto de sucesioes y series de úmeros reales, mediate las istruccioes Limit y, que os permitirá, e la mayoría
Cap ³tulo 6. Series Num ericas. Problemas resueltos. 6.1 Series num ericas. De niciones. Salvador Vera Ballesteros
 Cap ³tulo 6 Series Num ericas. Problemas resueltos Salvador Vera Ballesteros www.satd.uma.es/matap/svera 6. Series um ericas. De icioes De ici o 6. (Serie) Dada ua sucesi o um erica i ita: fa g fa ;a ;a
Cap ³tulo 6 Series Num ericas. Problemas resueltos Salvador Vera Ballesteros www.satd.uma.es/matap/svera 6. Series um ericas. De icioes De ici o 6. (Serie) Dada ua sucesi o um erica i ita: fa g fa ;a ;a
4. Series, Taylor y límites indeterminados
 4 Series, Taylor y ites idetermiados 4 Series de úmeros reales Queremos hacer sumas de ifiitos úmeros reales, llamadas series: a + a + a + = a = Por ejemplo, sumemos /5+/5 +/5 +/5 4 +/5 5 + Sumar u úmero
4 Series, Taylor y ites idetermiados 4 Series de úmeros reales Queremos hacer sumas de ifiitos úmeros reales, llamadas series: a + a + a + = a = Por ejemplo, sumemos /5+/5 +/5 +/5 4 +/5 5 + Sumar u úmero
PROGRESIONES ARITMÉTICAS.-
 PROGRESIONES ARITMÉTICAS.- Ua progresió aritmética es ua sucesió de úmeros tales que cada uo de ellos, excepto el primero, se obtiee sumado al aterior ua costate d, que se deomia diferecia de la progresió.
PROGRESIONES ARITMÉTICAS.- Ua progresió aritmética es ua sucesió de úmeros tales que cada uo de ellos, excepto el primero, se obtiee sumado al aterior ua costate d, que se deomia diferecia de la progresió.
