Acta Universitaria ISSN: Universidad de Guanajuato México
|
|
|
- Yolanda Sevilla Godoy
- hace 7 años
- Vistas:
Transcripción
1 Acta Uivrsitaria ISSN: Uivrsidad d Guaajuato México Guía-Caldró, M.; Rosals-García, J. J.; Guzmá-Cabrra, R.; Gozálz-Parada, A.; Álvarz-Jaim, J. A. El cálculo difrcial itgral fraccioario y sus aplicacios Acta Uivrsitaria, vol. 25, úm. 2, marzo-abril, 25, pp Uivrsidad d Guaajuato Guaajuato, México Dispoibl : Cómo citar l artículo Númro complto Más iformació dl artículo Págia d la rvista rdalyc.org Sistma d Iformació Citífica Rd d Rvistas Citíficas d América Latia, l Carib, España y Portugal Proycto académico si fis d lucro, dsarrollado bajo la iiciativa d accso abirto
2 doi:.574/au El cálculo difrcial itgral fraccioario y sus aplicacios Th diffrtial ad itgral fractioal calculus ad its applicatios M. Guía-Caldró*, J. J. Rosals-García*, R. Guzmá-Cabrra*, A. Gozálz-Parada*, J. A. Álvarz-Jaim* RESUMEN Durat los últimos 2 años, l cálculo d ord arbitrario (mjor coocido la litratura como cálculo d ord fraccioario) s ha dsarrollado d mara imprsioat. Si mbargo, México o hay grupos cosolidados l studio y su aplicació. El objtivo d st trabajo s dar a coocr los orígs y l dsarrollo dl cálculo fraccioario, co la fialidad d motivar a los futuros ivstigadors a icursioar sta ára ta itrsat dl aálisis matmático o covcioal. Fialmt, como jmplo, s aaliza l movimito vrtical d ua partícula l so d u mdio dod la rsistcia s proporcioal a la vlocidad. ABSTRACT Ovr th last 2 yars arbitrary ordr calculus (bttr kow i th litratur as fractioal calculus) has b dvlopd imprssivly. Howvr, i Mxico thr ar o solid groups dvotd to its study ad applicatios. Th objtiv of this work is to prst th origis ad dvlopmt of fractioal calculus, i ordr to courag futur rsarchrs to vtur ito this vry itrstig ara of ucovtioal mathmatical aalysis. Fially, as a xampl, vrtical motio of a particl withi a mdium whr rsistac is proportioal to spd is aalizd. INTRODUCCIÓN Rcibido: 23 d ovimbr d 24 Acptado: 2 d marzo d 25 Palabras clav: Drivadas itgrals fraccioarias; cuacios difrcials fraccioarias. Kywords: Fractioal diffrtias ad itgrals; fractioal diffrtial quatios. Cómo citar: Guía-Caldró, M., Rosals-García, J. J., Guzmá- Cabrra, R., Gozálz-Parada, A. & Álvarz- Jaim, J. A. (25). El cálculo difrcial itgral fraccioario y sus aplicacios. Acta Uivrsitaria, 25(2), doi:.574/au E l studio dl cálculo s aprd alguos métodos d drivació itgració, así como la gra importacia qu ti stas hrramitas matmáticas la cicia igiría. S aprd, d igual forma, qu la drivació y la itgració so opracios ivrsas ua d la otra y difir ua o varias costats, dpdido dl ord d la drivada. Si (d /dx ) f ( x) D f ( x) rprsta la -ésima drivada d la fució f (x) co rspcto a x, co, 2,..., tocs I f ( x) f ( xdx ) D f ( x) rprstará la -ésima itgral o itgral itrada d la misma fució f (x). Si mbargo, los opradors d drivació itgració vistos los cursos uivrsitarios ha sido d ord tro, 2,... Esto s lo qu coocmos como cálculo difrcial itgral ordiario o d ord tro. Aquí surg alguas prgutas: por qué db sr, 2, 3,...,?, xistirá la posibilidad d qu sa /2, /3,...? El objtivo pricipal d st trabajo s, admás d dar a coocr la historia dl cálculo d ord fraccioario dsd las futs históricas origials, compltar cirtas xprsios scritas libros y artículos cuado trata sobr la historia y orig dl cálculo d ord fraccioario. Por jmplo, la xprsió Así s ti qu d :2 x srá igual a x 2 d x : x o mustra l razoamito d Libiz (859) para stablcr la drivada fraccioaria d ord u mdio d x; o bi, La rfrcia a ua drivada fraccioaria u libro d txto aparc por primra vz 89 l libro dl matmático fracés S. F. Lacroix ( ). El libro, d casi 7 págias, ddica dos * Dpartamto d Igiría Eléctrica, Divisió d Igirías, Campus Irapuato-Salamaca, Uivrsidad d Guaajuato. Carrtra Salamaca-Vall d Satiago km km, comuidad d Palo Blaco, Salamaca, Guaajuato, México, C.P Tl.: (464) , xt y Corros lctróicos: guia@ugto.mx; rosals@ugto.mx; guzmac@ugto.mx 2 Vol. 25 No. 2 Marzo-Abril 25
3 págias [ ], qu si vr si quira l ídic dl libro d Lacroix (89) l atribuy la dfiició d la drivada d ord fraccioario u mdio; otra xprsió comú s: Eulr solo mcioa pro o da jmplos i aplicacios d la drivada d ord fraccioario, si lr ralidad l txto complto dl documto a qu s hac rfrcia st mismo trabajo (Eulr, 738). Por tal motivo, s cosidra importat st trabajo dar u poco más d iformació sobr los documtos origials dod qudó scrito l psamito d Libiz, Eulr, Liouvill y Rima. S prsta, admás, ua aplicació co la qu s aaliza l movimito vrtical d ua partícula l so d u mdio dod la rsistcia s proporcioal a la vlocidad (Rosals, Guía, Martíz & Balau, 23), co l propósito d motivar al lctor para qu s iici l studio dl cálculo d ord fraccioario. Brv historia dl cálculo fraccioario El acimito dl cálculo d ord fraccioario tuvo lugar dspués d la publicació, 675, d u documto d G. W. Libiz, dod aparcía l símbolo d y/dx, l cual s rfir a la drivada d ord d la fució y rspcto d x, dod s u úmro atural. Si mbargo, tdrá stido xtdr los valors d al cojuto d los úmros racioals, irracioals o compljos? G. W. Libiz (646-76), al rspodr a ua carta d G. F. Atoi, marqués d l Hôpital (64-74), custioa sobr qué sucdría si fura /2. El 3 d sptimbr d 695 cotsta d mara ituitiva: sto coduciría apartmt a ua paradoja d la cual algú día srá xtraídas coscucias muy útils (Libiz, 859). E sta misma carta, Libiz da ua aproximació a lo qu podría sr ua drivada fraccioaria, poido como jmplo la drivada /2 d x. El razoamito d Libiz s l siguit: Sa dada la ordada x progrsió gométrica d modo qu si s ti ua costat d b sa dx xd b : a, o (sustituydo a por la uidad) dx xd b, ahora ddx srá x dβ 2 y d 3 x srá x dβ 3 tcétra y d x xdβ. Y d sta forma l xpot difrcial s cambiado por xpot potcia rmplazado dx : x por d b s tdrá d x d x : x x. Así s ti qu d :2 x srá igual a x 2 d x : x (Libiz, 859). E otació actual, la dfiició qu propo Libiz para la drivada d ord fraccioario d x stá dada por:, () y para l caso particular /2 s tdrá:. Si mbargo, la primra rfrcia a ua drivada fraccioaria aparc, por primra vz, u artículo scrito por Lohard Eulr (77-783) tr y publicado 738, dod aplica su fórmula d itrpolació dl factorial tr úmros tros positivos para dar ua dfiició d la drivada d ord fraccioario. El razoamito d Eulr s l siguit: s trata d ivstigar la rlació tr d (z ) y dz co dz costat. Supo primro qu s u tro y si, z [ / ( )]z, si 2, ( )z 2 [ / ( 2)]z 2, si 3, ( )( 2)z 3 [ / ( 3)] z 3, gral, d z /dz [ / ( )]z. Pro d x( l x) y (-) d x( l x), por lo tato: d( ) d z z z d x( l x), (2) d x( l x) dod los límits d itgració so x como límit ifrior y x como límit suprior. E (2) dbrá actualizars la simbología l para. Dspués d Adri- Mari Lgdr ( ) s usa la otació Γ ( + ) para la itgral dl umrador y Γ( + ) para la itgral dl domiador. Es posibl ralizar alguas opracios algbraicas co (2) para comparar la dfiició d la drivada d ua fució potcia co dfiicios más rcits y, a la vz, para hacr otar la difrcia co la dfiició propusta por Libiz (859). La cuació dada por (2) tambi pud sr scrita como: quivalt a scribir: d z dz, (3) Γ ( + ) z. (4) Γ( + ) Car soyt ls ordés x progrssio Gomtriqu sort qu prat u costat db soit dx xdb: a, ou (prat a pour l uité) dx xdb, alors ddx sra x db 2, dβ t d 3 x sra x db 3 tc. t d x xdb. Et par ctt adrss l xposat diffrtil st chagé xposat pottil t rmttat dx : x pour db, il aura d x dx : x x dβ dβ. Aisi il s suit qu d :2 2 dβ x sra gal à x dx : x. El cálculo difrcial itgral fraccioario y sus aplicacios M. Guía-Caldró, J. J. Rosals-García, R. Guzmá-Cabrra, A. Gozálz-Parada, J. A. Álvarz-Jaim pp Vol. 25 No. 2 Marzo-Abril 25 2
4 Multiplicado umrador y domiador d (4) por Γ ( ) s obti: d z dz x z ( ) ( ) Γ + Γ B ( ) ( ) ( +, ), (5) Γ + Γ Γ ( ) dod B( +, ) B(, + ) s la fució bta, dfiida por: Γ B(, ) B(, ) ( ) Γ ( ) Γ( + ) d z dz t ( t) dt. (6) + Sustituydo (6) (5) y hacido zt u s obti: z u + Γ ( ) ( z u) + du. (7) Si o s u tro, tocs (7) s la fórmula d Eulr (738) para ua drivada fraccioaria d ua fució potcia, y qudaría como sigu: yd /2 z z d y, () la curva buscada s obti d la siguit mara: y zd z z y y zd z z y d 2 2 d l A A A z c yl z cay A. () y E l libro d S. F. Lacroix mcioado ats s icluy l artículo publicado por Eulr, l cual s dfi la drivada d ord fraccioario d ua fució potcia. Así, pus, s pud dcir qu a Eulr s l db la primra fórmula para la drivada fraccioaria d ua fució potcia. E 822, su libro Théori Aalytiqu d la Chalour (822), Ja-Baptist Josph Fourir (768-83) idica qu difrcials itgrals d ord arbitrario i pud sr obtidas a partir d la cuació:, (2) α d x dx α β x β u + Γ ( α) ( x u) α+ du. (8) y obsrvado qu la i-ésima drivada d la fució coso difir sólo l sigo y l factor p i, s obti: La xistcia d la drivada fraccioaria d ord a stá dtrmiada por la covrgcia d la itgral (8). Eulr (738) tambié da u jmplo para y /2 y obti, la simbología actual: d /2 z l xdx l xdx zd z zdz, (9) A dod A s l ára d u círculo d diámtro igual a la uidad. Tambié s pud utilizar la cuació (4) para obtr: Para fializar, Eulr (738) propo la siguit cuació difrcial fraccioaria para dtrmiar la forma d la curva dada por la cuació:. dp, (3) dod i pud sr cualquir catidad: positiva o gativa. Así, pus, Fourir (822) prsta ua fórmula gral para la drivació itgració fraccioaria. Ua fució tdrá drivada o itgral fraccioaria si las itgrals impropias covrg. Si mbargo, o prsta jmplos d aplicació i dsarrolla u tratado complto sobr l cálculo itgro-difrcial d ord fraccioario. Idica, admás, l mismo libro, qu sus rsultados sobr las drivadas itgrals d ord fraccioario ya los había publicado co atrioridad ua Mémoir sur ls vibratios ds surfacs élastiqus, lu à la séac d l Académi ds Scics, l 6 jui 86 (art. VI, t, t art. VII, 3 t 4) (Fourir, 822). Ua d las primras aplicacios a la física s proporcioada por Nils Hrik Abl (82-829). El 22 Vol. 25 No. 2 Marzo-Abril 25 El cálculo difrcial itgral fraccioario y sus aplicacios M. Guía-Caldró, J. J. Rosals-García, R. Guzmá-Cabrra, A. Gozálz-Parada, J. A. Álvarz-Jaim pp. 2-27
5 problma cosist cotrar la forma d la curva sobr u plao vrtical, tal qu u objto, al dslizars si fricció sobr lla, llgu al fial d su rcorrido u timpo qu sa idpdit dl lugar qu comic l movimito. Si l timpo d caída s ua costat coocida, la cuació itgral d Abl (839a) ti la forma: /2 f (t)dt. (4) E ralidad, Abl studió cuacios itgrals co úclos d la forma ( x -t) a (Abl, 839b), sido la cuació (4) u caso particular cuado a /2. Para dtrmiar la fució dscoocida f (x) (4), Abl (839a) scribió la part drcha d (4) como:. (5) Dspués, tomado la drivada /2 ambos lados d la cuació obtuvo:, (6) ya qu los opradors fraccioarios (drivadas itgrals co cirtas codicios sobr f ) satisfac la propidad D /2 D /2 f D f f. Etocs, calculado la drivada d ord /2 d la costat k (6) s dtrmia la fució f (x). Est rsultado d Abl (839a) s cosidra u gra logro para l dsarrollo postrior dl cálculo d ord fraccioario. Es importat hacr otar qu la drivada d ord fraccioario d ua costat o simpr s cro. Drivada fraccioaria d Liouvill Josph Liouvill (832) hac rfrcia, Mémoir sur qustios d Gométri t d Mécaiqu, a los trabajos d Eulr, Laplac, Fourir y al libro d cálculo d Lacroix; tambié hac rfrcia a la cuarta carta d Libiz a Wallis (Libiz, 832), auqu s basa más los trabajos d Laplac (82) y Fourir (822) para hacr su dsarrollo dl cálculo itgro-difrcial d ord fraccioario. Liouvill (832) part d la drivada d ord tro d la fució xpocial, sto s: m d x ax d a m ax, (7) m dod idica qu m pud sr cualquir úmro ral o compljo, positivo (idicado la drivació) o gativo (idicado la itgració). Partido, pus, d sta dfiició d la drivada, y supoido qu ua fució y s pud dsarrollar ua sri d xpocials, stablc ua fórmula gral para la drivada. Primro dsarrolla y sri d xpocials: m x y å A i, (8) i i y driva térmio a térmio sta sri para obtr:. (9) A la xprsió (9) s l cooc como la primra dfiició d drivada fraccioaria d Liouvill. E la misma mmoria, Liouvill (832) da dos jmplos, qu alguos historiadors ha llamado como la sguda dfiició d Liouvill. El primr jmplo s para la fució y /x, tato qu l sgudo s ua gralizació dl primro y /x, sto s:. (2) Es importat otar qu (2) o s más qu la trasformada d Laplac (82) d la fució scaló uitario la qu s ha cambiado s por x. Partido d (2), Liouvill (832) utiliza la fórmula para la drivada d ord fraccioario y obti: Para l sgudo jmplo, dfi:. (2), (22). (23) A cotiuació, Liouvill (832) da ua xprsió para la itgral fraccioaria d ua fució arbitraria, pro co rstriccios:, (24) dod µ > y si φ mx ( ) A y m db sr mor qu cro o si s d la forma m p + q, p db sr mayor qu cro. Al fial d cutas lo qu s trata s d El cálculo difrcial itgral fraccioario y sus aplicacios M. Guía-Caldró, J. J. Rosals-García, R. Guzmá-Cabrra, A. Gozálz-Parada, J. A. Álvarz-Jaim pp Vol. 25 No. 2 Marzo-Abril 25 23
6 cuidar la covrgcia d la itgral impropia d la drcha (24), qu s logra cuado l itgrado s aula, d acurdo co Liouvill (832)., (27) Para obtr la drivada d φ(x), Liouvill (832) hac µ p, dod s l mor tro positivo mayor qu µ, co lo qu obti:. (25) Liouvill (832) ha llgado a la misma coclusió a la qu había llgado Fourir (822) diciséis años ats: la drivada d ord fraccioario s ua itgral dfiida, sto coducirá, como s vrá más adlat, a u uvo puto d partida la dfiició d la drivada d ord fraccioario. Liouvill (832), la misma mmoria, aplica la fórmula para rsolvr varios problmas d ltrodiámica, gomtría y mcáica. Ats d cotiuar co st uvo foqu qu trata a la drivada d ord fraccioario como ua itgral, sguirmos al foqu propusto por Grüwald-Létikov. Drivada fraccioaria d Grüwald-Létikov Ato Karl Grüwald (838-92), 867, y Alksy Vasilivich Létikov ( ), 868, propo la dfiició d la drivada fraccioaria, partido d la dfiició básica d la drivada d ord tro; sto s:. (28) Las fórmulas (27) y (28) so muy útilis l cálculo umérico d la drivada d ord fraccioario; stas fórmulas a < x s l puto dsd dod s calculará la drivada corrspodit al puto x. Otro puto d partida para dfiir la drivada d ord fraccioario fu propusto por Liouvill (832), qui, partido d la itgral dl ord fraccioario, obti:, (29) dod a < x. La cuació s pud obtr d (8) hacido u f ( t), sustituydo a por a y u por t. Ahora b bi, si < a < s pud hacr a v, tocs s ti:. (3),, La drivada fraccioaria stá dfiida, st caso, si la itgral covrg, dbido a qu, sgú s vio al iicio d sta scció, Liouvill (832) dsarrolla f (t) ua sri d xpocials. La itgral (3) covrg si a, las parts rals d las potcias d so mayors qu cro y x >. dod! m!( m)! Γ ( + ) Γ ( m + ) Γ( m + )., (26) Drivada fraccioaria d Rima Brhard Rima ( ), u mauscrito dl 4 d ro d 898, su época d studiat y publicado forma póstuma, propo:. (3) Hacido alguas opracios aritméticas s llga a las siguits fórmulas d la drivada fraccioaria d Grüwald-Létikov: Para la fórmula (3), Rima (898) dsarrolla f (t) ua sri d potcias, por lo qu l límit ifrior st caso s k. A la cuació: 24 Vol. 25 No. 2 Marzo-Abril 25 El cálculo difrcial itgral fraccioario y sus aplicacios M. Guía-Caldró, J. J. Rosals-García, R. Guzmá-Cabrra, A. Gozálz-Parada, J. A. Álvarz-Jaim pp. 2-27
7 . (32) S l llama fórmula para la drivada d ord fraccioario d Rima-Liouvill, para c y para c, rspctivamt. Drivada fraccioaria d Caputo E 969, l físico matmático italiao Michl Caputo dio ua uva dfiició d drivada d ord fraccioario qu prmitía itrprtar físicamt las codicios iicials d los cada vz más umrosos problmas aplicados qu s staba studiado. Caputo (969) dfiió la drivada fraccioaria como:, (33) dod < a < y f () s ua drivada ordiaria. La rlació tr ambas dfiicios (32) y (33) d la drivada d ord fraccioario stá dada por:. (34) S pud otar qu la dfiició d la drivada d ord fraccioario propusta por Michl Caputo (969) s más rstrictiva qu la d Rima-Liouvill, ya qu l primr caso la fució db sr drivabl, lo qu o rquir la sguda dfiició. La trasformada d Laplac d la drivada fraccioaria d Rima-Liouvill (32) y d Caputo (33) stá dadas por las xprsios: L, (35) L, (36) dod F(s) s la trasformada d Laplac d f(t). Obsrv qu la xprsió (35) coti codicios iicials fraccioarias, lo cual ti dificultads d itrprtació la aplicació a problmas físicos, mitras qu la xprsió (36) ti codicios iicials ordiarias, s dcir, o fraccioarias, ya qu f (k) () so drivadas ordiarias (k, 2, 3,...). Ésta s ua d las razos por las cuals los problmas d aplicació s usa frcutmt la drivada fraccioaria d Caputo (969) (36). Exist, actualmt, dos aplicacios pricipals dl cálculo d ord fraccioario: aplicacios al cotrol y aplicacios d modlado matmático. Esta última aplicació icluy l aálisis, simulació, disño, tcétra. Cuado s habla d modlado matmático s icluy, prfrtmt, aqullos fómos cuyos modlos d ord tro o satisfac los datos xprimtals, por jmplo fómos d difusió aómala: sub-difusió y supr-difusió, viscolasticidad, suprcoductividad, cácr, tcétra. E st puto surg alguos custioamitos: cuál s la itrprtació física d ua drivada y/o itgral fraccioaria?, por qué hay difrts dfiicios d drivada itgral fraccioaria? E l cálculo ordiario, stas prgutas stá bi claras y ti ua itrprtació muy lgat gométrica y físicamt. Si mbargo, l caso dl cálculo fraccioario aú stas prgutas o stá compltamt rsultas, así qu hay mucho trabajo por hacr. E la siguit scció damos u jmplo scillo y dtallado d aplicació dl cálculo fraccioario. Movimito vrtical u campo gravitacioal S aalizará, como u jmplo d aplicació dl cálculo fraccioario, l caso d ua partícula movimito vrtical l so d u mdio, dod la rsistcia s proporcioal a la vlocidad. Supógas qu ua partícula s laza hacia abajo co ua vlocidad iicial v dsd ua altura h u campo gravitacioal costat. La cuació d movimito s tocs (Thorsto & Mario, 24): d m v v mg mkv kv g d t d +, (37) dt dod k s ua costat positiva rsposabl d la furza d rsistcia co uidads d sgudos ivrsos, s, y mkv rprsta ua furza dirigida hacia arriba, ya qu tomamos z y v z positivos s stido, y l movimito s dirig hacia abajo; o sa v < d forma qu mkv >. Si la codició iicial s cosidra v() v, dod v s la vlocidad iicial dl curpo caydo, la solució s:. (38) El cálculo difrcial itgral fraccioario y sus aplicacios M. Guía-Caldró, J. J. Rosals-García, R. Guzmá-Cabrra, A. Gozálz-Parada, J. A. Álvarz-Jaim pp Vol. 25 No. 2 Marzo-Abril 25 25
8 Dado qu v dz/dt s itgra ua vz más, tomado cuta la codició iicial z() h, como rsultado s obti:. (39) La xprsió (38) idica qu a mdida qu l timpo crc ( t, ) la vlocidad s va aproximado al valor vt () g/ k, la cual s llamada vlocidad fial o vlocidad trmial v f. Por otro lado, s v la cuació (37) qu cuado lla s hac v - g/ k, s cosigu l mismo rsultado, pus tocs la furza s aula y dsaparc la aclració. Cuado l módulo d la vlocidad iicial sa mayor qu l d la vlocidad fial, l curpo comzará a movrs prdido vlocidad y v tdrá hacia l valor d la vlocidad fial dsd l stido cotrario. Ahora s aalizará l problma atrior dsd l puto d vista dl cálculo fraccioario. Para llo s hará alguas modificacios, como s mustra (4), ats d pasar a la cuació difrcial d ord fraccioario, a partir d (37). Estas modificacios cosist ormalizar las variabl v y t tomado como bas d ormalizació g/k y /k para la vlocidad y l timpo, rspctivamt, d forma qu dividido v tr g/k : Rsolvido rspcto a U(s) rsulta: g us Us ( ) s + +. (43) g g s( s + ) Ahora, aplicado la trasformada ivrsa d Laplac (Podluby, 999; Samko, Kilbas & Marichv, 993) s ti:, (44) dod s ha usado las fórmulas (Moj, Ch, Viagr, Xu & Fliu-Batl, 2) L, (45) L. (46) Volvido a las variabls v(t) y t s ti:. (47). (4) Esta cuació difrcial s pud scribir tambié fució d ua uva variabl dpdit y adimsioal, rprstada por u, mitras qu la variabl tmporal, adimsioal, idpdit s t kt. S ti, tocs: γ d u u dτ +. (4) γ E sta cuació difrcial d ord fraccioario, las variabls u y t so adimsioals. Aplicado la trasformada d Laplac (Podluby, 999; Samko, Kilbas & Marichv, 993) co la codició u() u y k/g, obtmos: sus ( ) u s U( s) g g +. (42) s Ahora, supoido qu: w u( ) d β τ β dτ dod t kt, w u k - g v. β β Us ( ) sws ( ) s w(), (48) kz() kz kh, w() y g g g Sustituydo U(s) d (48) (43) y rsolvido para W(s) s ti: w Ws ( ) s + u s s β γ β s + + s. (49) β+ γ s + γ γ Fialmt, s aplica la trasformada ivrsa d Laplac (82) a (49) y s raliza las opracios csarias para volvr a las variabls, t y z. 26 Vol. 25 No. 2 Marzo-Abril 25 El cálculo difrcial itgral fraccioario y sus aplicacios M. Guía-Caldró, J. J. Rosals-García, R. Guzmá-Cabrra, A. Gozálz-Parada, J. A. Álvarz-Jaim pp. 2-27
9 dod < βγ,., (5) Si (5) s da valors d a b y g, s rcupra (39). Si (5) s hac β γ, s obti:. (5) Hoy día, l cálculo fraccioario s ha aplicado difrts áras d las cicias igirías, física, biología, química, gología, toría d cotrol, lctromagtismo, léctrica, circuitos léctricos, procsamito d imágs y sñals, óptica, tcétra, y xist xclts libros qu trata sobr su rcit dsarrollo y aplicacios como so: Balau, Güvc & Triro (2), Dithlm (2), Duart (2), Maiardi (2) y Tarasov (2), CONCLUSIÓN E st trabajo s ha prstado las distitas dfiicios d la drivada itgral d ord fraccioario. Estas difrts dfiicios xist por o habr u cocso gralizado sobr qué so la drivada itgral d ord fraccioario d ua fució; s dcir, o hay ua itrprtació física y gométrica cosistt sobr llas. Si mbargo, los modlos dscritos por cuacios difrcials d ord fraccioario, co las propidads d o localidad y mmoria, rprsta forma más adcuada sistmas compljos htrogéos qu los modlos d ord tro, como s mustra l jmplo prstado para l movimito vrtical u campo gravitatorio. REFERENCIAS Abl, N. H. (839a). Résolutio d u problèm d mécaiqu. Ouvrs Complèts (tomo prmir, pp. 27-3). Grödah: Christiaa. Abl, N. H. (839b). Sur qulqus itégrals défiis. Ouvrs Complèts (tomo scod, pp. 93-2). Grödah: Christiaa. Balau, D., Güvc Z. B. & Triro, M. J. A. (2). Nw Trds i Naotchology ad Fractioal Calculus Applicatios (544 pp.). Dordrcht Hidlbrg Lodo Nw York: Sprigr. Caputo, M. (969). Elasticità Dissipazio. Bologa: Zaichlli. Dithlm, K. (2). Th Aalysis of Fractioal Diffrtial Equatios (248 pp.). Dordrcht Hidlbrg Lodo Nw York: Sprigr. Duart, O. M. (2). Fractioal Calculus for Scitists ad Egirs (4 pp.). Dordrcht Hidlbrg Lodo Nw York: Sprigr. Eulr, L. (738). D progrssioibvs trascdtibvs, sv qvarvm trmii grals algbraic dari qvt, Commtarii Acadmia Scitiarvm Imprialis Ptropolit A A (tomo V, pp ). Sa Ptrsburgo. Fourir Josph, J. B. (822). Théori Aalytiqu d la Chalur (pp ). Paris: Chz Firmi Didot, Pèr t fils. Grüwald, A. K. (867). Ubr, Bgrzt, Drivatio ud Dr Awdug, Zitschrift für Mathmatik ud Physik, 2, Lacroix, S. F. (89). Traité du calcul différtil t du calcul itégral. Scod éditio, rvu t augmté (pp. 49-4). Paris: Courcir. Laplac, P. S. (82). Théori Aalytiqu ds Probabilitiés. M. V. Coucir, Librair pour ls Mathématiqus, quis ds Agustis, 57. Paris: Imprimur. Libiz, G. (859). Mathmatisch Schrift. Brlí: Vrlag vo A. Ashr & Comp. Libiz, G. (832). Cuarta carta a Wallis. Ouvrs complèts (tom III, 5 pp.). Paris. Létikov, A.V. (868). Thory of diffrtiatio of a arbitrary ordr, Mat. Sb., 3, -68. Liouvill, J. (832). Mémoir sur qustios d Gométri t d Mécaiqu, t sur u ouvau gr d Calcul pour résoudr cs Qusios. Joural d l Ecol Polytchiqu, 2(3), -66 y Maiardi, F. (2). Fractioal Calculus ad Wavs i Liar Viscolsticity (368 pp). Ed. Imprial Collg Prss. Moj, C. A., Ch, Y., Viagr, B. M., Xu, D. & Fliu-Batl, V. (2). Fractioal Ordr Systms ad Cotrols, Fudamtals ad Applicatios. Lodrs: Sprigr-Vrlag Lodo Limitd. Podluby, I. (999). Fractioal Diffrtial Equatios. Sa Digo: Acadmic Prss. Rosals García, J. J., Guía Caldró, M., Martíz Ortiz, J. & Balau, D. (23). Motio of a Particl i a Rsistig Mdium Usig Fractioal Calculus Approach. Procdigs of th Romaia Acadmy, 4(), Rima, B. (898). Ouvrs mathématiqus d Rima. París: Gauthir-villar. Samko, S. G., Kilbas, A. A. & Marichv, O.I. (993). Fractioal Itgrals ad Drivativs, Thory ad Applicatios. Laghor, PA: Gordo ad Brach Scic Publishrs. Tarasov, V. E. (2). Fractioal Dyamics; Applicatios of th Fractioa Calculus to Dyamics of Particls, filds ad Mdia (522 pp.). Dordrcht Hidlbrg Lodo Nw York: Sprigr. Thorsto, S. T. & Mario, J. B. (24). Classical Dyamics of Particls ad Systms. Ed. Thomso Brooks/col. El cálculo difrcial itgral fraccioario y sus aplicacios M. Guía-Caldró, J. J. Rosals-García, R. Guzmá-Cabrra, A. Gozálz-Parada, J. A. Álvarz-Jaim pp Vol. 25 No. 2 Marzo-Abril 25 27
EXPONENTES Y POTENCIAS Muchos números se expresan en forma más conveniente como potencias de 10. Por ejemplo: m n n 0,2 3 3
 Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Universidad de Costa Rica. Instituto Tecnológico de Costa Rica. Determinar si las integrales impropias convergen o divergen.
 Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
2. Utilizando el método adimensional basado en el factor de calidad Q, determine:
 Uivrsidad Simó Bolívar Dpartamto d Covrsió y Trasport d Ergía Autor: Eduardo Albaz. Cart: 06-391 Profsor: J. M. Allr Máquias Eléctricas II CT-311 U motor d iducció coxió strlla d 100 kw, 416 V, rdimito
Uivrsidad Simó Bolívar Dpartamto d Covrsió y Trasport d Ergía Autor: Eduardo Albaz. Cart: 06-391 Profsor: J. M. Allr Máquias Eléctricas II CT-311 U motor d iducció coxió strlla d 100 kw, 416 V, rdimito
1 Realizar los ejercicios resueltos números 1 y 2 del tema 3 de Integración de. 2 Terminar los ejercicios de la práctica realizada este día.
 Est documto coti las actividads o prscials propustas al trmiar la clas dl día qu s idica. S sobrtid qu tambié s db ralizar l studio d lo plicado clas auqu o s icluya sa tara st documto. Clas 5 d ovimbr
Est documto coti las actividads o prscials propustas al trmiar la clas dl día qu s idica. S sobrtid qu tambié s db ralizar l studio d lo plicado clas auqu o s icluya sa tara st documto. Clas 5 d ovimbr
al siguiente límite si existe: . Se suele representar por ( x )
 UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA 1: Problema Nº 5.34 Oppenheim
 SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS
 UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
Señales y Sistemas. Análisis de Fourier.
 Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
11 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS)
 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
a a lim i) L< 1 absoluta convergencia absoluta convergencia convergencia condicional divergencia > r.
 (Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
(Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
Se llama sucesión a un conjunto de números dados ordenadamente de modo que se puedan numerar: primero, segundo, tercero,...
 TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
2.8.3 Solución de las ecuaciones diferenciales lineales no homogéneas por el método de variación de parámetros
 .8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
MATEMÁTICAS Y CULTURA B O L E T Í N No. 273 COORDINACIÓN DE MATEMÁTICAS APLICACIONES DEL DETERMINANTE DE VANDERMONDE
 MATEMÁTICAS Y CULTURA B O L E T Í N 23.04.20 No. 273 COORDINACIÓN DE MATEMÁTICAS MATEMÁTICAS MATEMÁTICAS APLICACIONES DEL DETERMINANTE DE VANDERMONDE E l Boltí Matmáticas Y Cultura No. 257 dl 23 d abril
MATEMÁTICAS Y CULTURA B O L E T Í N 23.04.20 No. 273 COORDINACIÓN DE MATEMÁTICAS MATEMÁTICAS MATEMÁTICAS APLICACIONES DEL DETERMINANTE DE VANDERMONDE E l Boltí Matmáticas Y Cultura No. 257 dl 23 d abril
TEMA 1: CALCULO DIRECTO DE LÍMITES
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
Cap. II: Principios Fundamentales del Flujo de Tránsito
 Cap. II: Pricipios Fudamtals dl Flujo d Trásito Diagrama Espacio-Timpo Distacia 1 2 Itralo (i) 3 4 5 6 Espaciamito () Timpo Flujo, q Dsidad, Vlocidad, Tasa horaria quialt a la cual trasita los hículos
Cap. II: Pricipios Fudamtals dl Flujo d Trásito Diagrama Espacio-Timpo Distacia 1 2 Itralo (i) 3 4 5 6 Espaciamito () Timpo Flujo, q Dsidad, Vlocidad, Tasa horaria quialt a la cual trasita los hículos
Respuesta en frecuencia. Procesado Digital de Señales.4º Ingeniería Electrónica. Universitat de València. Profesor Emilio Soria.
 Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
TEMA 2. ESPACIOS Y OPERADORES LINEALES CONTENIDO
 TEMA. ESPACIOS Y OPERADORES LINEALES CONTENIDO ESPACIOS LINEALES SOBRE UN CAMPO INDEPENDENCIA LINEAL, BASES Y CAMBIOS DE BASES OPERADORES LINEALES Y SUS REPRESENTACIONES SISTEMAS DE ECUACIONES ALGEBRÁICAS
TEMA. ESPACIOS Y OPERADORES LINEALES CONTENIDO ESPACIOS LINEALES SOBRE UN CAMPO INDEPENDENCIA LINEAL, BASES Y CAMBIOS DE BASES OPERADORES LINEALES Y SUS REPRESENTACIONES SISTEMAS DE ECUACIONES ALGEBRÁICAS
PROBLEMAS TEMA 4 EJERCICIO 1 (Ej 9.15 de Fernández Abascal)
 PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
TEMA 2 SUCESIONES. Tema 2 Sucesiones Matemáticas I 1º Bach. 1 SUCESIONES Y TÉRMINOS
 Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
MATEMÁTICA D Módulo I: Análisis de Variable Compleja. Teoría de Residuos
 Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Integral Indefinida o Antiderivada
 Dpartamto d Matmática Aplicada Cálculo II (0) Smstr -08 Profsor: José Luis Quitro Marzo 08 FACULTAD DE INGENIERÍA UNIVERSIDAD CENTRAL DE VENEZUELA Itgral Idfiida o Atidrivada. Comprub los siguits rsultados
Dpartamto d Matmática Aplicada Cálculo II (0) Smstr -08 Profsor: José Luis Quitro Marzo 08 FACULTAD DE INGENIERÍA UNIVERSIDAD CENTRAL DE VENEZUELA Itgral Idfiida o Atidrivada. Comprub los siguits rsultados
TEMA 5: LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS
 Dpartamto d Matmáticas. IE.S. Ciudad d Arjoa º Bach Socials. LÍMITES Propidads: TEMA : LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS. LÍMITES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES. RESOLUCIÓN DE INDETERMINACIONES.
Dpartamto d Matmáticas. IE.S. Ciudad d Arjoa º Bach Socials. LÍMITES Propidads: TEMA : LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS. LÍMITES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES. RESOLUCIÓN DE INDETERMINACIONES.
El cálculo diferencial e integral fraccionario y sus aplicaciones The differential and integral fractional calculus and its applications
 ISSN 88-6266 oi:.574/au.25.688 El cálculo ifrcial itral fraccioario y sus aplicacios Th iffrtial a itral fractioal calculus a its applicatios M. Guía-Calró*, J. J. Rosals-García*, R. Guzá-Cabrra*, A. Gozálz-Paraa*,
ISSN 88-6266 oi:.574/au.25.688 El cálculo ifrcial itral fraccioario y sus aplicacios Th iffrtial a itral fractioal calculus a its applicatios M. Guía-Calró*, J. J. Rosals-García*, R. Guzá-Cabrra*, A. Gozálz-Paraa*,
Sistemas de ecuaciones diferenciales lineales
 695 Aálisis matmático para Igiría M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA CAPÍTULO Sistmas d cuacios difrcials lials d primr ord Cuado s studia matmáticamt ua situació d la ralidad, l modlo qu s
695 Aálisis matmático para Igiría M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA CAPÍTULO Sistmas d cuacios difrcials lials d primr ord Cuado s studia matmáticamt ua situació d la ralidad, l modlo qu s
1.- a) Hallar a y b para que la siguiente función sea continua en x = 1:
 .- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
.- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Tema 8. Limite de funciones. Continuidad
 . Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
8 Límites de sucesiones y de funciones
 Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
EJERCICIOS PROPUESTOS. rectángulos obtenidos tomando como base la longitud de cada subintervalo y como altura la ordenada del extremo derecho.
 6 Itgral dfiida Ejrcicio rsulto EJERCICIOS PROPUESTOS Obté, co l método visto, l ára dl trapcio limitado por la rcta y +, l j X y las vrticals y Calcula l ára gométricamt y compara los rsultados S divid
6 Itgral dfiida Ejrcicio rsulto EJERCICIOS PROPUESTOS Obté, co l método visto, l ára dl trapcio limitado por la rcta y +, l j X y las vrticals y Calcula l ára gométricamt y compara los rsultados S divid
Matemáticas Aplicadas a las Ciencias Sociales II. Análisis: Derivadas Tema 6. Derivadas 1. Derivada de una función en un punto
 Matmáticas Aplicadas a las Cicias Socials II Aálisis: Drivadas Tma 6 Drivadas Drivada d ua fució u puto Tasa d variació d ua fució S llama tasa d variació mdia d ua fució f (), l itrvalo [a, b], al valor
Matmáticas Aplicadas a las Cicias Socials II Aálisis: Drivadas Tma 6 Drivadas Drivada d ua fució u puto Tasa d variació d ua fució S llama tasa d variació mdia d ua fució f (), l itrvalo [a, b], al valor
TALLER 4: Preparación parcial final. Cálculo Integral. UdeA Profesor: Jaime Andrés Jaramillo.
 TALLER : Prparació parcial fial Cálculo Itgral UdA 5- Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d)
TALLER : Prparació parcial fial Cálculo Itgral UdA 5- Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d)
TALLER 4: Preparación parcial final. Cálculo Integral. UdeA Profesor: Jaime Andrés Jaramillo.
 TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
2. ALGEBRA LINEAL (2.1_AL_T_062, Revisión: , C12)
 . ALGEBRA LINEAL (._AL_T_06, Rvisió: 8-03-06, C). CONCEPTOS FUNDAMENTALES: ESPACIOS VECTORIALES, BASES, DIMENSIONES... INTRODUCCIÓN. Notació: utilizamos abcdario latio para vctors, grigo para scalars (úmros).
. ALGEBRA LINEAL (._AL_T_06, Rvisió: 8-03-06, C). CONCEPTOS FUNDAMENTALES: ESPACIOS VECTORIALES, BASES, DIMENSIONES... INTRODUCCIÓN. Notació: utilizamos abcdario latio para vctors, grigo para scalars (úmros).
El error con ese presupuesto será aproximadamente del 3,1% Ejercicio 8.2
 EJERCICIO 8.1 U ivstigador dispo d 0.000 para ralizar las trvistas d ua custa ua gra ciudad. El custioario s admiistrará mdiat trvistas tlfóicas, sido l cost d cada trvista d 0. Qué marg d rror dbrá asumir
EJERCICIO 8.1 U ivstigador dispo d 0.000 para ralizar las trvistas d ua custa ua gra ciudad. El custioario s admiistrará mdiat trvistas tlfóicas, sido l cost d cada trvista d 0. Qué marg d rror dbrá asumir
ANÁLISIS DE FOURIER CAPÍTULO CUATRO TIEMPO DISCRETO Introducción
 CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
RESULTADOS DE LA CARACTERIZACIÓN DE DOS MESAS A ÍNDICE DE ALTA EXACTITUD MEDIANTE UN MÉTODO DE AUTO-IDENTIFICACIÓN DE ERRORES
 RESULTADOS DE LA CARACTERIZACIÓN DE DOS MESAS A ÍNDICE DE ALTA EXACTITUD MEDIANTE UN MÉTODO DE AUTO-IDENTIFICACIÓN DE ERRORES Jua O Garduño, Edgar Arizmdi Ctro Nacioal d Mtrología (CENAM) Carrtra a los
RESULTADOS DE LA CARACTERIZACIÓN DE DOS MESAS A ÍNDICE DE ALTA EXACTITUD MEDIANTE UN MÉTODO DE AUTO-IDENTIFICACIÓN DE ERRORES Jua O Garduño, Edgar Arizmdi Ctro Nacioal d Mtrología (CENAM) Carrtra a los
! 1 3 <1 la serie converge (y confirma a n! 0 ). a n. x 2 >0; f 0 (x)<0 si x>1; R 1 f (x)dx = 1 2 e x2 1 = 1 2e. ) Convergente. n! 0 ) Convergente.
 Solucios d los roblmas d Matmáticas (07-08) {a } acotada ifriormt or 0 (los a so ositivos) y dcrcit us + + )9líma a ) a a ) a0 Como a + a < la sri covrg (y cofirma a 0 ) a) (a ) / Divrgt (O orqu {a
Solucios d los roblmas d Matmáticas (07-08) {a } acotada ifriormt or 0 (los a so ositivos) y dcrcit us + + )9líma a ) a a ) a0 Como a + a < la sri covrg (y cofirma a 0 ) a) (a ) / Divrgt (O orqu {a
Estabilidad de Sistemas No-lineales: Sistema de Nivel de Líquidos de Dos Tanques Interconectados.
 6 RIEE&C, REVISTA DE INGENIERÍA ELÉCTRICA, ELECTRÓNICA Y COMPUTACIÓN, Vol. 5 No., DICIEMBRE 008 Estabilidad d Sistmas No-lials: Sistma d Nivl d Líquidos d Dos Taqus Itrcoctados. Azurz M. Jua, Padilla G.
6 RIEE&C, REVISTA DE INGENIERÍA ELÉCTRICA, ELECTRÓNICA Y COMPUTACIÓN, Vol. 5 No., DICIEMBRE 008 Estabilidad d Sistmas No-lials: Sistma d Nivl d Líquidos d Dos Taqus Itrcoctados. Azurz M. Jua, Padilla G.
Análisis y resolución del régimen transitorio de circuitos de corriente continua
 Aálisis y rsolució dl régim rasiorio d circuios d corri coiua solució d cuacios difrcials. Dfiició Ua cuació difrcial lial, ordiaria, d ord y a coficis cosas rlacioa las ésimas drivadas d ua fució x(,
Aálisis y rsolució dl régim rasiorio d circuios d corri coiua solució d cuacios difrcials. Dfiició Ua cuació difrcial lial, ordiaria, d ord y a coficis cosas rlacioa las ésimas drivadas d ua fució x(,
DECAIMIENTO RADIOACTIVO
 DECIMIETO RDIOCTIVO El dcaimito radioactivo s idpdit dl modo d dcaimito, y s aplica a todos llos: α,β +, β -, CE (captura lctróica), γ, y fisió spotáa. Postulados: LEY DE DESITEGRCIO RDIOCTIV. La probabilidad
DECIMIETO RDIOCTIVO El dcaimito radioactivo s idpdit dl modo d dcaimito, y s aplica a todos llos: α,β +, β -, CE (captura lctróica), γ, y fisió spotáa. Postulados: LEY DE DESITEGRCIO RDIOCTIV. La probabilidad
CÁLCULO NUMÉRICO ( )
 CÁLCULO NUMÉRICO (808068) Tma. Fudamtos d la Toría d Errors Octubr 0. Al studiar l fómo diario d la variació qu primta las codicios mtorológicas, s suprim muchas variabls qu dbría d itrvir los cálculos.
CÁLCULO NUMÉRICO (808068) Tma. Fudamtos d la Toría d Errors Octubr 0. Al studiar l fómo diario d la variació qu primta las codicios mtorológicas, s suprim muchas variabls qu dbría d itrvir los cálculos.
UNIVERSIDAD CATÓLICA DE SANTA MARÍA
 VICRRCTORADO ACADÉMICO UIVRSIDAD CATÓLICA D SATA MARÍA PLA D STUDIOS VIGT DSD / SCULA : CICIAS IGIRIAS FISICAS Y FORMALS IGIRIA LCTROICA ASIGATURA TIP CR JF T. PRRQUISITOS QUIVALCIAS SMSTR : MTODOLOGIA
VICRRCTORADO ACADÉMICO UIVRSIDAD CATÓLICA D SATA MARÍA PLA D STUDIOS VIGT DSD / SCULA : CICIAS IGIRIAS FISICAS Y FORMALS IGIRIA LCTROICA ASIGATURA TIP CR JF T. PRRQUISITOS QUIVALCIAS SMSTR : MTODOLOGIA
CASO DE ESTUDIO N 8. Análisis de un tornillo de transmisión
 Vrsió 01 CAPITULO POYECTO DE ELEMENTOS DE SUJECIÓN, ANCLAJE Y CIEE CASO DE ESTUDIO N 8 Aálisis u torillo trasmisió Vrsió 01 1. Itroucció Los torillos trasmisió stá somtios a cosirabls solicitacios bias
Vrsió 01 CAPITULO POYECTO DE ELEMENTOS DE SUJECIÓN, ANCLAJE Y CIEE CASO DE ESTUDIO N 8 Aálisis u torillo trasmisió Vrsió 01 1. Itroucció Los torillos trasmisió stá somtios a cosirabls solicitacios bias
Análisis de Señales Capítulo III: Transformada de Fourier discreta. Profesor: Néstor Becerra Yoma
 Aálisis d Sñals Capíulo III: Trasormada d Fourir discra Prosor: ésor Bcrra Yoma 3. Torma dl Musro Gra dsarrollo d la compuació > digializació d sñals mdia musro, posrior rcosrucció d la sñal Codició csaria
Aálisis d Sñals Capíulo III: Trasormada d Fourir discra Prosor: ésor Bcrra Yoma 3. Torma dl Musro Gra dsarrollo d la compuació > digializació d sñals mdia musro, posrior rcosrucció d la sñal Codició csaria
Capítulo IV. Estadísticas cuánticas.
 Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
Tema 5: Transistor Bipolar de Unión (BJT)
 Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
4.1 Procedimientos de inferencia para la distribución exponencial
 4 Ifrca paramétrca 4 Procdmtos d frca para la dstrbucó xpocal La dstrbucó xpocal fu la prmra dstrbucó para modlar tmpos d falla y para lla s ha dsarrollado métodos stadístcos d mara xtsva a T ua va xpocal
4 Ifrca paramétrca 4 Procdmtos d frca para la dstrbucó xpocal La dstrbucó xpocal fu la prmra dstrbucó para modlar tmpos d falla y para lla s ha dsarrollado métodos stadístcos d mara xtsva a T ua va xpocal
5 MECÁNICA ESTADÍSTICA CUÁNTICA DE GASES IDEALES
 ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
Tema 5: Transistor Bipolar de Unión (BJT)
 Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
Política Fiscal. Gobiernos de coalición o de intereses geográficos dispersos
 Política Fiscal Goiros d coalició o d itrss oráficos disrsos Goiros d coalició o d itrss oráficos disrsos Escario olítico dod l oiro stá comusto or dos artidos coalició:. Partidos ti rfrcias distitas sor
Política Fiscal Goiros d coalició o d itrss oráficos disrsos Goiros d coalició o d itrss oráficos disrsos Escario olítico dod l oiro stá comusto or dos artidos coalició:. Partidos ti rfrcias distitas sor
ESTIMADOR DE AITKEN Y PROPIEDADES DEL MISMO (Última revisión: 1 de marzo de 2007)
 Apts d clas d coomtría II / 6 STIMADOR D AITKN Y ROIDADS DL MISMO Última rvisió: d marzo d 7 rof. Rafal d Arc rafal.darc@am.s stimació d los parámtros dl MBRL por máxima vrosimilitd Apoádoos la hipótsis
Apts d clas d coomtría II / 6 STIMADOR D AITKN Y ROIDADS DL MISMO Última rvisió: d marzo d 7 rof. Rafal d Arc rafal.darc@am.s stimació d los parámtros dl MBRL por máxima vrosimilitd Apoádoos la hipótsis
FAyA Licenciatura en Química Física III año 2006 MECANICA CUANTICA
 FAyA Licciatura Química Fíica III año 006 MECANICA CUANTICA E la mcáica cláica l tado d u itma dcrib u itat dtrmiado dado toda u coordada q y u vlocidad q. E mcáica cuática l tado d u itma dfi dado ua
FAyA Licciatura Química Fíica III año 006 MECANICA CUANTICA E la mcáica cláica l tado d u itma dcrib u itat dtrmiado dado toda u coordada q y u vlocidad q. E mcáica cuática l tado d u itma dfi dado ua
PROYECCIÓN CÓNICA CONFORME DE LAMBERT Prof. Ricardo Martínez Morales
 CARTOGRAFÍA MATEMÁTICA PROYECCIÓN CÓNICA CONFORME DE LAMBERT Prof. Ricardo Martíz Morals INTRODUCCIÓN El físico, astróomo y matmático alsaciao J.H.Lambrt tuvo ua prolífica producció l ára d la cartografía
CARTOGRAFÍA MATEMÁTICA PROYECCIÓN CÓNICA CONFORME DE LAMBERT Prof. Ricardo Martíz Morals INTRODUCCIÓN El físico, astróomo y matmático alsaciao J.H.Lambrt tuvo ua prolífica producció l ára d la cartografía
Tema 5. Análisis de Fourier para Señales y Sistemas Discretos.
 Tma 5. Aálisis d Fourir para Sñals y Sistmas Discrtos. E l tma 3 hmos hcho u studio d los sistmas discrtos l domiio tmporal. Esto os ha prmitido ralizar ua caractrizació d los mismos y hacr u studio d
Tma 5. Aálisis d Fourir para Sñals y Sistmas Discrtos. E l tma 3 hmos hcho u studio d los sistmas discrtos l domiio tmporal. Esto os ha prmitido ralizar ua caractrizació d los mismos y hacr u studio d
CÁLCULO DE LÍMITES. Por otro lado es importante distinguir en el cálculo de límites, los casos indeterminados de los determinados: = ; = ; =
 CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
Prob PI-1. Forma débil de un problema de flujo de calor estacionario en 2D (Cálculos a mano) T k. Q y
 p Q S d ds d S q d ds d ] [ ] [ ] ([ d Q d ] [ j i Prob PI-. Forma débil d u problma d flujo d calor stacioario D (Cálculos a mao Cosidérs l problma dfiido la figura siguit: La EDP asociada s: co Q ua
p Q S d ds d S q d ds d ] [ ] [ ] ([ d Q d ] [ j i Prob PI-. Forma débil d u problma d flujo d calor stacioario D (Cálculos a mao Cosidérs l problma dfiido la figura siguit: La EDP asociada s: co Q ua
Un ejercicio relacionado con la función Li(x)
 Uivrsidad Iramricaa d Puro Rico - Rcio d Poc U jrcicio rlacioado co la fució Por: Eriqu Díaz Gozálz Uivrsidad Iramricaa d Puro Rico, Rcio d Poc. U poco d hisoria. E la búsquda para ua l qu idicara la disribució
Uivrsidad Iramricaa d Puro Rico - Rcio d Poc U jrcicio rlacioado co la fució Por: Eriqu Díaz Gozálz Uivrsidad Iramricaa d Puro Rico, Rcio d Poc. U poco d hisoria. E la búsquda para ua l qu idicara la disribució
Teoría de Sistemas y Señales
 Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
MATEMÁTICA AVANZADA TRABAJO PRÁCTICO N O 1
 MATEMÁTICA AVANZADA TRABAJO PRÁCTICO N O Fcios aalíticas Dmostrar q s aalítica todo l plao complo Z. Siglaridads d a ció Estdiar las siglaridads d las sigits cios calclado límit: a b c 9 cos d 7 Trasormació
MATEMÁTICA AVANZADA TRABAJO PRÁCTICO N O Fcios aalíticas Dmostrar q s aalítica todo l plao complo Z. Siglaridads d a ció Estdiar las siglaridads d las sigits cios calclado límit: a b c 9 cos d 7 Trasormació
CINEMÁTICA (TRAYECTORIA CONOCIDA)
 1º Bachillrato: Cinmática (trayctoria conocida CINEMÁTICA (TRAYECTORIA CONOCIDA (Todos los datos y cuacions, n unidads dl S.I. 1. Un objto tin un moviminto uniform d rapidz 4 m/s. En l instant t=0 s ncuntra
1º Bachillrato: Cinmática (trayctoria conocida CINEMÁTICA (TRAYECTORIA CONOCIDA (Todos los datos y cuacions, n unidads dl S.I. 1. Un objto tin un moviminto uniform d rapidz 4 m/s. En l instant t=0 s ncuntra
1.- Estudie el carácter de la serie numérica. 1 es divergente, la serie n propuesta será divergente. Solución.- Puesto que, n = 1, 2, 3,...
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
Tabla de contenido. Página
 Tabla d coido Págia Opradors difrcials sismas d cuacios Opradors difrcials Oprador aulador 6 fiició 6 Sismas d cuacios difrcials lials 9 Solució d u sisma, méodo d los opradors 9 Rsum 5 Bibliografía rcomdada
Tabla d coido Págia Opradors difrcials sismas d cuacios Opradors difrcials Oprador aulador 6 fiició 6 Sismas d cuacios difrcials lials 9 Solució d u sisma, méodo d los opradors 9 Rsum 5 Bibliografía rcomdada
1 OTRA MANERA DE VISUALIZAR LA EXPANSIÓN DE UN GAS
 Toría dl Gas Ral 0 OTRA MAERA DE VISUALIZAR LA EXPASIÓ DE U GAS. Itroducció E l prst capítulo s ivita al lctor a aalizar d otra mara la pasió o comprsió d u gas. E bas a sta mara difrt d ivolucraros l
Toría dl Gas Ral 0 OTRA MAERA DE VISUALIZAR LA EXPASIÓ DE U GAS. Itroducció E l prst capítulo s ivita al lctor a aalizar d otra mara la pasió o comprsió d u gas. E bas a sta mara difrt d ivolucraros l
Variables aleatorias discretas
 Probabilidads y stadística Comutació Facultad d Cicias actas y aturals. Uivrsidad d Buos Airs Aa M. Biaco y la J. Martíz 4 Variabls alatorias discrtas istribució Biomial: Muchos rimtos alatorios satisfac
Probabilidads y stadística Comutació Facultad d Cicias actas y aturals. Uivrsidad d Buos Airs Aa M. Biaco y la J. Martíz 4 Variabls alatorias discrtas istribució Biomial: Muchos rimtos alatorios satisfac
Tema 11. Limite de funciones. Continuidad
 Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS
 Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
Fenómenos de enlace atómico en una dimensión
 Joural of Basic Scics Vol. ( Mayo-gosto 05 Fómos d lac atómico ua dimsió E. Ruda Solis Divisió cadémica d Igiría y rquitctura Uivrsidad Juárz utóoma d Tabasco C.P. 86690 Cuduacá Tabasco Mx. rudas@gmail.com
Joural of Basic Scics Vol. ( Mayo-gosto 05 Fómos d lac atómico ua dimsió E. Ruda Solis Divisió cadémica d Igiría y rquitctura Uivrsidad Juárz utóoma d Tabasco C.P. 86690 Cuduacá Tabasco Mx. rudas@gmail.com
Fallas de la aproximación estática. cristal
 Diámica d la rd Foos Fallas d la aproximació stática para l cristal Propidads térmicas dl quilibrio: Calor spcífico: Las vibracios d la rd so la pricipal causa d absorció d calor y da cuta dl calor spcífico
Diámica d la rd Foos Fallas d la aproximació stática para l cristal Propidads térmicas dl quilibrio: Calor spcífico: Las vibracios d la rd so la pricipal causa d absorció d calor y da cuta dl calor spcífico
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
SÍLABO DEL CURSO DE AUDITORIA DE MARKETING
 SÍLABO DEL CURSO DE AUDITORIA DE MARKETING I. INFORMACIÓN GENERAL: 1.1 Facultad: Ngocios 1. Carrra Profsioal: Admiistració y Marktig 1.3 Dpartamto: ------------- 1.4 Rquisito: Dircció Comrcial 1.5 Priodo
SÍLABO DEL CURSO DE AUDITORIA DE MARKETING I. INFORMACIÓN GENERAL: 1.1 Facultad: Ngocios 1. Carrra Profsioal: Admiistració y Marktig 1.3 Dpartamto: ------------- 1.4 Rquisito: Dircció Comrcial 1.5 Priodo
La gama con sistema HE dispone de un control digital táctil basado en 4 modos de funcionamiento: automático, eco, confort y alta emisión (boost).
 Radiadors d baja tmpratura Nuva gama d radiadors d altísima misió icluso co salto térmico 30ºC. Idals tato para obra uva como para mrcado d rposició. Válidos para istalacios bitubo o mootubo. Fácil matimito
Radiadors d baja tmpratura Nuva gama d radiadors d altísima misió icluso co salto térmico 30ºC. Idals tato para obra uva como para mrcado d rposició. Válidos para istalacios bitubo o mootubo. Fácil matimito
Tema 2. Derivada. Técnicas de Derivación. Raúl González Medina. I.E. Juan Ramón Jiménez Tema 2
 Tma Drivaa. Técicas Drivació 0.- Itroucció.- Tasa Variació Mia.- Drivaa ua ució u puto..- Drivaas Latrals...- Itrprtació gométrica la rivaa..- Rlació tr cotiuia y rivabilia..- Sigiicao graico la rivaa.
Tma Drivaa. Técicas Drivació 0.- Itroucció.- Tasa Variació Mia.- Drivaa ua ució u puto..- Drivaas Latrals...- Itrprtació gométrica la rivaa..- Rlació tr cotiuia y rivabilia..- Sigiicao graico la rivaa.
Problemas Tema 2: Sistemas
 SISTEMAS Y CIRCUITOS ~ PROBLEMAS Curso Académico 00900 Problmas Tma Sismas PROBLEMA. Dados los siguis sismas impo coiuo las sñals d rada idicadas, drmi las sñals d salida corrspodis ( ) x sñal d rada x
SISTEMAS Y CIRCUITOS ~ PROBLEMAS Curso Académico 00900 Problmas Tma Sismas PROBLEMA. Dados los siguis sismas impo coiuo las sñals d rada idicadas, drmi las sñals d salida corrspodis ( ) x sñal d rada x
Observación: si en la urna hubiese 1500 bolillas blancas y 500 verdes y se extraen dos bolillas al azar sin reemplazo, entonces
 art Variabls alatorias rof. María B. itarlli.- Variabls alatorias discrtas imortats Distribució biomial Sa ε u xrimto alatorio. Sa u vto asociado a ε y aotamos Suogamos u xrimto alatorio ε u cuml los siguits
art Variabls alatorias rof. María B. itarlli.- Variabls alatorias discrtas imortats Distribució biomial Sa ε u xrimto alatorio. Sa u vto asociado a ε y aotamos Suogamos u xrimto alatorio ε u cuml los siguits
De la medición surge un valor, llamado valor de la magnitud y que indica el número de veces que la unidad elegida está contenida en la magnitud.
 Máquias, Métodos y Cotrol Dimsioal dl Procsamito METROLOGÍA MECÁNICA MEDICIONES Dfiició: Efctuar ua mdició, sigifica cotrar la distacia tr dos putos dados. Est caso s l más frcut, cuado las mdicios s rfir
Máquias, Métodos y Cotrol Dimsioal dl Procsamito METROLOGÍA MECÁNICA MEDICIONES Dfiició: Efctuar ua mdició, sigifica cotrar la distacia tr dos putos dados. Est caso s l más frcut, cuado las mdicios s rfir
FÓRMULAS PARA LA ESTIMACIÓN DE LA CAPACIDAD
 APÉNDICE: FÓRMULAS PARA LA ESTIMACIÓN DE LA CAPACIDAD Fórmula uificada d Kimbr Kimbr aglutia la xpricia d muchos años d sayos ralizados por l TRRL Gra Brtaña y propo ua fórmula uificada para l cálculo
APÉNDICE: FÓRMULAS PARA LA ESTIMACIÓN DE LA CAPACIDAD Fórmula uificada d Kimbr Kimbr aglutia la xpricia d muchos años d sayos ralizados por l TRRL Gra Brtaña y propo ua fórmula uificada para l cálculo
Fonones: Cuantización de las vibraciones de la red cristalina.
 Foo: Cuatizació d la ibracio d la rd critalia. Oda d logitud larga Oda lática... Oda d logitud corta λ a o πa tmo qu tr cuta la tructura atómica dl crital. foó logitudial foó traral a mooatómica: Coidrmo
Foo: Cuatizació d la ibracio d la rd critalia. Oda d logitud larga Oda lática... Oda d logitud corta λ a o πa tmo qu tr cuta la tructura atómica dl crital. foó logitudial foó traral a mooatómica: Coidrmo
Respuesta al escalón unitario
 Rpua al caló uiario Epcificacio l domiio dl impo La ampliud duració d la rpua raioria db mar dro d lími olrabl dfiido E ima d corol lial la caracrizació dl raiorio comúm raliza uilizado u caló uiario a
Rpua al caló uiario Epcificacio l domiio dl impo La ampliud duració d la rpua raioria db mar dro d lími olrabl dfiido E ima d corol lial la caracrizació dl raiorio comúm raliza uilizado u caló uiario a
1 Ejemplos de Aproximaciones de Integrales con Sumas de Riemman
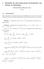 Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
Transformador VALORES NOMINALES Y RELATIVOS
 Tasfomado VAORE NOMNAE Y REATVO Nobto A. mozy VAORE NOMNAE as picipals caactísticas d las máquias vi dadas po los fabicats la domiada placa o chapa d caactísticas; dod s spcifica, t otas cosas, la potcia
Tasfomado VAORE NOMNAE Y REATVO Nobto A. mozy VAORE NOMNAE as picipals caactísticas d las máquias vi dadas po los fabicats la domiada placa o chapa d caactísticas; dod s spcifica, t otas cosas, la potcia
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
LECCIÓN 11 CÉLULAS SOLARES
 ÓN CÉUAS SOAS NTODUÓN tr los dispositivos basados smicoductors, la célula solar s uo d los más adcuados para tdr cómo las propidads itríscas básicas dl smicoductor, combiació co las propidads tríscas coscucia
ÓN CÉUAS SOAS NTODUÓN tr los dispositivos basados smicoductors, la célula solar s uo d los más adcuados para tdr cómo las propidads itríscas básicas dl smicoductor, combiació co las propidads tríscas coscucia
Página 76. Página 78. Página 77. Página 79. Y de la primera: 1. Resolvemos por sustitución: a) Despejo x de la primera y la sustituyo en la segunda:
 Solucios d ls ctividds Pági 6. Rsolvmos por sustitució: ) Dspjo d l primr l sustituo l sgud: ( ) 8 0 Co lo cul: ( ) b) Si multiplico l primr por -, obtgo: + 8 Co lo cul tgo dos rcts coicidts, s dcir, l
Solucios d ls ctividds Pági 6. Rsolvmos por sustitució: ) Dspjo d l primr l sustituo l sgud: ( ) 8 0 Co lo cul: ( ) b) Si multiplico l primr por -, obtgo: + 8 Co lo cul tgo dos rcts coicidts, s dcir, l
TEMA 2 MODELO DE REGRESIÓN LINEAL SIMPLE
 TEMA MODELO DE REGRESIÓN LINEAL SIMPLE. INTRODUCCIÓN A LA REGRESIÓN SIMPLE! 4 Supogamos qu la varal s ua fucó lal d otra varal, dod la rlacó tr y dpd d parámtros! y! dscoocdos. Itroduccó a la Rgrsó Smpl!
TEMA MODELO DE REGRESIÓN LINEAL SIMPLE. INTRODUCCIÓN A LA REGRESIÓN SIMPLE! 4 Supogamos qu la varal s ua fucó lal d otra varal, dod la rlacó tr y dpd d parámtros! y! dscoocdos. Itroduccó a la Rgrsó Smpl!
15. FUNCIONES ESPECIALES Y CARÁCTER DE DIRICHLET
 Rafal Parra Machío 5. 5. Fucio Aritmética. Fucio Aditiva y Multiplicativa. Ua fució aritmética ua fució d valor compljo dfiida lo tro poitivo. Dcimo qu f ua fució aditiva i f ( m) = f ( m) + f ( ), mcd(
Rafal Parra Machío 5. 5. Fucio Aritmética. Fucio Aditiva y Multiplicativa. Ua fució aritmética ua fució d valor compljo dfiida lo tro poitivo. Dcimo qu f ua fució aditiva i f ( m) = f ( m) + f ( ), mcd(
UNIVERSIDAD CATÓLICA DE SANTA MARÍA
 VICRRCTORADO ACADÉMICO UIVRSIDAD CATÓLICA D SATA MARÍA PLA D STUDIOS VIGT DSD / SCULA : CICIAS IGIRIAS FISICAS Y FORMALS IGIRIA IDUSTRIAL ASIGATURA TIP CR JF T. PRRQUISITOS QUIVALCIAS SMSTR : 9 COMUICACIO
VICRRCTORADO ACADÉMICO UIVRSIDAD CATÓLICA D SATA MARÍA PLA D STUDIOS VIGT DSD / SCULA : CICIAS IGIRIAS FISICAS Y FORMALS IGIRIA IDUSTRIAL ASIGATURA TIP CR JF T. PRRQUISITOS QUIVALCIAS SMSTR : 9 COMUICACIO
Definición de derivada
 Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
COLEGIO DE POSTGRADUADOS
 COLEGIO DE POSTGRADUADOS INSTITUCIÓN DE ENSEÑANZA E INVESTIGACIÓN EN CIENCIAS AGRÍCOLAS CAMPUS MONTECILLO SOCIOECONOMÍA, ESTADÍSTICA E INFORMÁTICA ESTADÍSTICA PRUEBAS DE BONDAD DE AJUSTE Y DE RAZÓN DE
COLEGIO DE POSTGRADUADOS INSTITUCIÓN DE ENSEÑANZA E INVESTIGACIÓN EN CIENCIAS AGRÍCOLAS CAMPUS MONTECILLO SOCIOECONOMÍA, ESTADÍSTICA E INFORMÁTICA ESTADÍSTICA PRUEBAS DE BONDAD DE AJUSTE Y DE RAZÓN DE
TEMA 5: Efectos de los Rectificadores sobre la red de alimentación.
 TEMA 5 : Efctos d los Rctificadors sobr la rd d alimtació TEMA 5: Efctos d los Rctificadors sobr la rd d alimtació. Ídic TEMA 5: Efctos d los Rctificadors sobr la rd d alimtació. 5..- Factor d Potcia....
TEMA 5 : Efctos d los Rctificadors sobr la rd d alimtació TEMA 5: Efctos d los Rctificadors sobr la rd d alimtació. Ídic TEMA 5: Efctos d los Rctificadors sobr la rd d alimtació. 5..- Factor d Potcia....
El transistor bipolar de unión (BJT)
 l rasisor biolar d uió (JT roducció 1948-1949: illia hockly, Joh ard y alr H. raai dscubr s disosiivo y modla su riciio d fucioamio. s l rasisor más uilizado circuios discros. Prsa mayors vlocidad d rsusa
l rasisor biolar d uió (JT roducció 1948-1949: illia hockly, Joh ard y alr H. raai dscubr s disosiivo y modla su riciio d fucioamio. s l rasisor más uilizado circuios discros. Prsa mayors vlocidad d rsusa
lm í d x = lm í ln x + x 1 H = lm í x + e x 2
 Autovaluación Página 8 Calcula los siguints límits: a) lm í c m b) lm í ccotg m c) lm í sn d) lm í ( ) / 8 ln 8 8 ln ( cos ) 8 a) lm í 8 c ln ln H ( / ) lm í ( )ln 8 ln m lm í 8 H lm í / 8 b) lm í 8 dcotg
Autovaluación Página 8 Calcula los siguints límits: a) lm í c m b) lm í ccotg m c) lm í sn d) lm í ( ) / 8 ln 8 8 ln ( cos ) 8 a) lm í 8 c ln ln H ( / ) lm í ( )ln 8 ln m lm í 8 H lm í / 8 b) lm í 8 dcotg
Transformada de Laplace
 Traformada d Laplac Traformada d Laplac Dada ua fució d variabl cotiua f, u traformada bilatral d Laplac dfi como: t [ f ] f dt L dod ua variabl complja, σ iω Para qu ta itgral covrja, dcir, para qu ita
Traformada d Laplac Traformada d Laplac Dada ua fució d variabl cotiua f, u traformada bilatral d Laplac dfi como: t [ f ] f dt L dod ua variabl complja, σ iω Para qu ta itgral covrja, dcir, para qu ita
INSTITUTO DE CIENCIAS MATEMÁTICAS CÁLCULO DIFERENCIAL. TERCERA EVALUACIÓN Septiembre 17 de Nombre:
 INSTITUTO DE CIENCIAS MATEMÁTICAS CÁLCULO DIFERENCIAL TERCERA EVALUACIÓN Sptimbr 7 d Nombr: Parallo: Firma: TEMA ( puntos) Justificando su rspusta, califiqu como vrdadra o falsa, cada proposición: a) La
INSTITUTO DE CIENCIAS MATEMÁTICAS CÁLCULO DIFERENCIAL TERCERA EVALUACIÓN Sptimbr 7 d Nombr: Parallo: Firma: TEMA ( puntos) Justificando su rspusta, califiqu como vrdadra o falsa, cada proposición: a) La
Implementación de un Regulador PID
 Tma 3 Implmntación d un Rgulador PID Gijón - Marzo 22 .4 Accions d Control Clásicas.2 x(t).8.6 x(t) (t) _ P I D 2 3 u(t) Sistma.4.8.6.4.2-5 5 5 2 25 3 (t) -.2 -.4-5 5 5 2 25 3 2.8 - Proporcional ( t) =
Tma 3 Implmntación d un Rgulador PID Gijón - Marzo 22 .4 Accions d Control Clásicas.2 x(t).8.6 x(t) (t) _ P I D 2 3 u(t) Sistma.4.8.6.4.2-5 5 5 2 25 3 (t) -.2 -.4-5 5 5 2 25 3 2.8 - Proporcional ( t) =
