Unidad 7. Trigonometría
|
|
|
- Rubén Méndez Montes
- hace 6 años
- Vistas:
Transcripción
1 Págin Resuelve. ) Rzon que l estc y su sombr formn un triángulo rectángulo. Ocurre lo mismo con cd árbol y su sombr? b) Por qué se hn de dr pris en señlr los etremos de ls sombrs? Rzon que todos los triángulos formdos por un árbol, o l estc, y sus correspondientes sombrs en cd instnte son semejntes. c) Sbiendo que hy un chopo cuy sombr midió,9 m, hll su ltur. ) L estc es verticl y el suelo es horizontl. L sombr se proyect sobre el suelo. Por tnto, l estc y su sombr son los ctetos de un triángulo rectángulo. EST Lo mismo ocurre con cd árbol y su sombr. (Los árboles hy que idelizrlos pr considerrlos como segmentos verticles). SOMR DE L EST b) Hy que señlr ls sombrs muy depris pr que no les fecte el movimiento del Sol. Los triángulos formdos por un estc y su sombr y por un árbol y su sombr siempre serán semejntes porque siempre serán rectángulos y comprtirán un ángulo gudo (el que corresponde l inclinción de los ryos del Sol). c) Longitud estc 6 cm Sombr de l estc 76 cm ltur del chopo Sombr del chopo,9 m 9 cm ,7 cm 8,07 m
2 Rzones trigonométrics de un ángulo gudo Págin. Dibuj sobre un ángulo como el nterior,, un triángulo rectángulo de tl modo que 00 mm. Hll sus rzones trigonométrics y observ que obtienes, proimdmente, los mismos vlores que en el ejemplo de rrib. 00 mm 6 mm sen cos 6 0, , mm tg 6 0,67 8. Dibuj, sobre un ángulo de, un triángulo rectángulo cuy hipotenus mid 0 cm. lcul, como en el ejemplo de rrib, ls rzones trigonométrics de. ómo son entre sí el seno y el coseno? uánto vle l tngente? Eplic por qué. 0 cm 7, cm sen cos tg 7, 0,7 0 7, 0,7 0 7, 7, 7, cm El triángulo demás de rectángulo es isósceles y, por tnto, los dos ctetos tienen l mism longitud, de hí que el seno y el coseno de sen igules y l tngente vlg.
3 Págin. Utilizndo un plntill de ppel milimetrdo como l de rrib y un trnsportdor de ángulos, clcul el seno y el coseno de 0, 0, 0, 0, 0, 60, 70 y 80, y l tngente de quellos que pueds. 0, O 0, U sen 0 0,8, cos 0 0,98, tg 0 0,8 sen 0 0,, cos 0 0,9, tg 0 0,7 sen 0 0,, cos 0 0,86, tg 0 0,8 sen 0 0,6, cos 0 0,76, tg 0 0,8 sen 0 0,76, cos 0 0,6 sen 60 0,86, cos 60 0, sen 70 0,9, cos 70 0, sen 80 0,98, cos 80 0,8
4 . lcul ls rzones trigonométrics, seno, coseno y tngente, de y comprueb que coinciden (ecepto decimles) con lo que clculste en el ejercicio de l págin nterior. D E 0, O 0, sen E cos O sen E sen 0,7 cos O cos 0,7 tg D D D tg O
5 Relciones trigonométrics fundmentles Págin 6. sen α 0,6. lcul cos α y tg α. sen α + cos α 0,6 + cos α cos α 0,6 tg α sen 8 cos cos α 0,6 tg 06, tg α 0,7 08, Por tnto, cos α 0,8 y tg α 0,7.. tg β 0,. lcul sen β y cos β. sen cos sen b b 0, 8 sen b 0, cos b b+ cos b tommos l ríz positiv cos α 0,8 (0,cos β) + cos β 0,809cos β + cos β,809cos β cos β sen β 0,cos β sen β 0,7 Por tnto, sen β 0,7 y cos β 0,88., 809 tommos l ríz positiv cos β 0,88
6 Págin 7. Teniendo en cuent que tg, deduce el vlor de sen y de cos medinte ls relciones fundmentles. sen ; sen cos cos (sen ) + (cos ) (cos ) + (cos ) cos ± ± Solo tommos el resultdo positivo: cos sen. Teniendo en cuent que sen 0 /, hll el vlor de cos 0 y de tg 0 medinte ls relciones fundmentles. sen 0 (sen 0 ) + (cos 0 ) + (cos 0 ) cos 0 ± Tommos el resultdo positivo: cos 0 tg 0 / /. lcul el seno y l tngente de un ángulo cuyo coseno vle 0,8. cos α 0,8 (sen α) + (cos α) (0,8) + (sen α) sen α ±0,6 Tommos solo el vlor positivo: sen α 0,6 tg α 06, 0,7 08, 6. Hll el seno y el coseno de un ángulo cuy tngente vle 0,7. tg α sen 0,7; sen α 0,7 cos α cos (sen α) + (cos α) (0,7cos α) + (cos α),9(cos α) cos α ±0,8 Solo tommos el vlor positivo: cos α 0,8 sen α 0,7 0,8 sen α 0,7 6
7 7. opi en tu cuderno y complet l siguiente tbl de rzones trigonométrics: sen α 0,9 / cos α 0,8 / tg α, En ls operciones donde prezcn frcciones o rdicles, trbj con ellos; no utilices su epresión deciml. En todos los csos, solo tomremos los resultdos positivos. sen α 0,9 cos α 0,8 (cos α) + (0,9) cos α 0, (sen α) + (0,8) sen α 0,7 tg α 09,,76 tg α 07, 0,69 0, 08, sen α tg α, c m + (cos α) cos α tg α / / cos α (sen α) + (sen α) + (cos α) sen sen α, cos α cos (,cos α) + (cos α) cos α 0,7 sen α, 0,7 sen α 0,96 e o sen α tg α sen ; sen α cos α cos tg α / / (sen α) + (cos α) (cos α) + (cos α) cos α sen α sen α 0,9 0,7 / 0,96 / / cos α 0, 0,8 / 0,7 / / tg α,76 0,69 /, / 7
8 Utilizción de l clculdor en trigonometrí Págin 8. Obtén ls siguientes rzones trigonométrics y escribe en tu cuderno los resultdos redondendo ls milésims. ) sen 86 b) cos 9 c) tg d) sen ' '' e) cos 9 7' f ) tg 86 ' g) sen 0 0'' (tención, 0 0' 0'') ) sen 86 0,998 b) cos 9 0, c) tg 0,0 d) sen ( ' ") 0,66 e) cos (9 7') 0,08 f) tg (86 ') 8,68 g) sen (0 0") 0,7 8
9 Págin 9. D el vlor del ángulo α en form segesiml, en cd cso: ) sen α 0,9 b) tg α,8 c) cos α 0, d) tg α 0, e) sen α 0,08 f ) cos α 0,88 ) α 6 0' 9" b) α 80 6' " c) α 6 9' " d) α 8 6' " e) α ' 9" f) α 8 ' 7". ) lcul sen α sbiendo que cos α 0,9. b) lcul cos α sbiendo que tg α 6,. c) lcul tg α sbiendo que cos α 0,06. d) lcul tg α sbiendo que cos α 0,96. e) lcul sen α sbiendo que tg α 0,. ) cos α 0,9 sen α 0, b) tg α 6, cos α 0, c) cos α 0,06 tg α 6,67 d) cos α 0,96 tg α 0,9 e) tg α 0, sen α 0,099 9
10 Resolución de triángulos rectángulos Págin 0. Los dos ctetos de un triángulo rectángulo miden 8 cm y 7 cm. Hll los dos ángulos gudos. 8 cm b 7 cm tg α 8 0,676 α ' 9,7" 7 β 90 ' 9,7" 86',7". En un triángulo rectángulo, un ángulo gudo mide 7, y el cteto opuesto, 87 m. Hll el otro cteto y l hipotenus. 87 m c 7 sen ,6 m sen 7 tg 7 87 c 87, m c tg 7. lcul el rdio de un octógono regulr de 0 cm de ldo. uánto mide su potem? r, 0 sen, 0 r r 0 6, cm sen, cos, potem potem, cm r. Hll l potem de un heptágono regulr de 0 cm de rdio. lcul tmbién l longitud del ldo. 0 cm α l/ α 60 : ' " cos ( ' ") 0 0 cos ( ' ") 9 cm sen ( ' ") l/ l 0 l Por tnto, el ldo del heptágono mide 8,68 cm y su potem 9 cm. 0 sen ( ' "), cm l 8,68 cm 0
11 Resolución de triángulos oblicuángulos Págin. En un triángulo, hll conociendo 7 cm, 0 cm y ^. 7 cm h cos 7,8 cm sen h h 9,6 cm 7 y 0 cm y 0 0,8 8,6 cm h + y 7,0 cm. Hll los ldos y de un triángulo en el que sbemos 00 cm, ^ y ^ 8. c h 8 H 00 Trzmos l ltur sobre y dividimos el triángulo & en dos triángulos rectángulos H & y H &. En H & : tg h 0, 900 h 8 En H & : tg 8 h 0, h h 0, 900 h 0, ( 00 ) onociendo y h podemos hllr los ldos 0,900 0,(00 ) 0,900, 0,,,, 6, cm, h,8 cm y. En H & : cos 6, c 6, c,7 cm c cos En H & : cos , 7, 77, cm cos 8 Por tnto, c,7 cm y 77, cm.
12 6 Rzones trigonométrics de 0 60 Págin. Indic el signo de cd un de ests rzones trigonométrics, situndo proimdmente los ángulos en l circunferenci goniométric: ) sen 8 b) cos 0 c) tg 00 d) cos 0 e) cos 0 f ) tg 9 g) cos 7 h) sen 8 i) tg 6 ) b) c) sen 8 < 0 cos 0 > 0 tg 00 < 0 d) e) f) cos 0 > 0 cos 0 < 0 tg 9 < 0 g) h) i ) cos 7 > 0 sen 8 > 0 tg 6 > 0. Indic en qué cudrnte se encuentr cd uno de los ángulos α, β, γ y ϕ: ) sen α < 0 y tg α > 0 b) cos β > 0 y tg β < 0 c) sen γ < 0 y cos γ < 0 d) cos ϕ > 0 y sen ϕ < 0 Qué signo tiene cd un de ls rzones trigonométrics que fltn? ) sen α < 0 α III o IV cudrnte tg α > 0 α I o III cudrnte demás, cos α < 0. α III cudrnte
13 b)cos β > 0 β I o IV cudrnte tg β < 0 β II o IV cudrnte β IV cudrnte demás, sen β < 0. c) sen γ < 0 γ III o IV cudrnte cos γ < 0 γ II o III cudrnte γ III cudrnte demás, tg γ > 0. d)cos ϕ > 0 ϕ I o IV cudrnte sen ϕ < 0 ϕ III o IV cudrnte ϕ IV cudrnte demás, tg ϕ < 0.. Dibuj sobre un circunferenci goniométric, en ppel milimetrdo, los ángulos siguientes: 6,, y 00 Represent sus rzones trigonométrics y d su vlor proimdo. sen 6 0,88 cos 6 0,7 tg 6,88 sen 0, cos 0,9 tg 0,9 sen 0,89 cos 0, tg,96 sen 00 0,87 cos 00 0, tg 00,7. En l págin nterior, en l circunferenci goniométric sobre l que se hn representdo el seno y el coseno, hy un triángulo coloredo, O'. ) Rzonndo sobre él y teniendo en cuent que O, justific que cos α O' y sen α. ' b) plicndo el teorem de Pitágors en este triángulo, justific que (sen α) + (cos α). c) Justific que (sen β) + (cos β), rzonndo sobre el correspondiente triángulo. ) cos α O ' O ' ' O O O b) (sen α) + (cos α) `' j + ` ' j `Oj c) (sen β) + (cos β) O. Di el vlor de sen α y cos α cundo α vle 0, 90, 80, 70 y 60. α sen α cos α 0 0
14 6. Teniendo en cuent l semejnz de los triángulos O' y OUT, y que OU, demuestr que: sen tg cos sen α T tg α α cos α O ' U Por l semejnz de triángulos: O' ' OU 8 UT ' OU ' tg α UT O' O' ' O' sen cos
15 7 Ángulos de medids culesquier. Rzones trigonométrics Págin. Epres con vlores comprendidos entre 80 y 80 estos ángulos: ) 87 b) 8 c)0 8 d) 80 omprueb con l clculdor que, en cd cso, coinciden ls rzones trigonométrics de uno y otro ángulo. ) sen 87 sen 7 0,60 cos 87 cos 7 0,799 tg 87 tg 7 0,7 b) sen 8 sen 8 0,88 cos 8 cos 8 0,69 tg 8 tg 8,88 c) sen 8 sen ( 9 ) 0,87 cos 8 cos ( 9 ) 0, tg 8 tg ( 9 ),66 d) sen 80 sen ( ) 0, cos 80 cos ( ) 0,906 tg 80 tg ( ) 0,66
16 8 Funciones trigonométrics. El rdián Págin. Ps rdines los siguientes ángulos: ) b) 00 c)00 d) 0 Epres el resultdo en función de π y, luego, en form deciml. Por ejemplo: 80 π rd, rd. ) π rd π rd 0, rd 60 6 b) π rd π rd,7 rd 60 9 c) 0 d) 0 0 π rd π rd,6 rd π rd π rd,6 rd Ps grdos los siguientes ángulos: ) 0, rd b), rd c) π rd d) π rd e),8 rd f ) π rd ) 0, rd 0, 60 π 8 9' 6" b), rd, 60 π 8 9' " c) π rd d) π rd 80 8, 60 e),8 rd π 7 8' 6" f) π rd
17 Págin 6. Verddero o flso? ) El rdián es un medid de longitud equivlente l rdio. b) Un rdián es un ángulo lgo menor que 60. c) Puesto que l longitud de l circunferenci es πr, un ángulo completo (60 ) tiene π rdines. d) 80 es lgo menos de rdines. e) Un ángulo recto mide π/ rdines. f) Ls funciones trigonométrics son periódics. g) Ls funciones sen y cos tienen un periodo de π. h) L función tg tiene periodo π. i) L función cos es como sen desplzd π/ l izquierd. ) Flso, el rdián es un unidd de medid de ángulos. Se llm rdián un ángulo tl que el rco que brc tiene l mism longitud que el rdio con el que se h trzdo. b) Verddero. rd 7 7' " c) Verddero. d) Flso. 80 π rd, rd e) Verddero. f) Verddero. g) Verddero. h) Verddero. i ) Verddero, se cumple sen b + π l cos α, α. 7
18 Págin 7 Hzlo tú. Repite el problem nterior suponiendo que el stélite ve l Tierr bjo un ángulo de 00. % % ) En este cso, TSO 0 y, por tnto, SOT 0. Siguiendo el mismo rzonmiento que en el libro de teto: d km cos 0 b) h R ( cos 0 ) 6 7 ( cos 0 ) 90, Áre del csquete πr h km El áre de l porción visible de l Tierr es de unos 60 millones de km. Hzlo tú. qué ltur hemos de subir pr ver un lugr situdo 00 km? d R S R 00 km T O, omo el cudrnte de meridino terrestre tiene km y corresponde un ángulo recto, l rco de 00 km le corresponde un ángulo de,. Siguiendo el mismo rzonmiento que en el ejercicio resuelto en el libro de teto: d 67 c m 9,7 km cos, Deberímos elevrnos unos 9 km. Hzlo tú. Repite el problem con estos dtos:.ª medición, 0 ; cmin 0 m;.ª medición,. Siguiendo el plntemiento del ejercicio resuelto del libro de teto: tg 0 y y tg y 9, 6,; y 7,77 y ( + 0) 07, El ncho del río es 6, m y l ltur del árbol, 7,77 m. 8
19 Ejercicios y problems Págin 8 Prctic Rzones trigonométrics de un ángulo gudo. Hll ls rzones trigonométrics del ángulo α en cd uno de estos triángulos: ) b) c) 7 m m α,6 cm ) sen α 7 7 0,8; cos α 0,96; tg α 7 0,9 b) sen α cos α c) sen α cos α 60 68, 6 8 8, 0,7, 6, 6 8 0,69; tg α, ,, , ,88; tg α 7 60 α 8 m 8 0,. Hll ls rzones trigonométrics de los ángulos gudos de los siguientes triángulos rectángulos (^ 90 ): ) b 6 cm; 6, cm b) b,6 cm; c, cm c) b 6 cm; 6 cm ) sen ^ 7, cm 6, cm cos ^ 6 0,90 6, m 6, 6 7, 0,8 6, 6, α 60 m 6 cm tg ^ 6,0 7, sen ^ 7, 0,8; cos ^ 6, 6 0,90; tg ^ 6, 7, 0,87 6 9
20 b) sen ^, cm,9 cm,6 cm cos ^, 6, +, 6, 0,, 9, 6 0,99, 9 sen ^, 0,; cos ^, 9 tg ^, 6 7,67,, 6 0,99; tg ^, 9, 9,9, c) sen ^ 6 6 cm cos ^ 6! 0, 6 6 cm, cm tg ^,,06 6, 6 0,896 sen ^ 6! 0, ; cos ^ 6, 0,896; tg ^ 6 6 0,96, % %. lcul ls rzones trigonométrics de los ángulos ^, ^, D y D. cm cm D 9 cm cm D 6 cm sen cos D D 0,8 0 0,6 9 0,6 6 0,8 0 ^ ^ 9 0,6 6 0,8 0 tg, 9! 6 0,7 0,8 0 0,6 6! 9 0,7, Relciones fundmentles. Si sen α 0,8, clcul cos α y tg α utilizndo ls relciones fundmentles (α < 90 ). cos α 0, 8 0,96; tg α 08, 0,9 096,. Hll el vlor ecto (con rdicles) de sen α y tg α sbiendo que cos α / (α < 90 ). sen α c m ; tg α 9 / / 0
21 6. Si tg α, clcul sen α y cos α (α < 90 ). sen s c cos sen cos + ( c) + c 8 6c 8 cos 6 sen α omplet en tu cuderno est tbl con ls rzones trigonométrics que fltn siendo α < 90. Utiliz rdicles cundo se posible. sen α 0,9 / cos α 0, / tg α 0,7 omo α < 90 sen α > 0, cos α > 0 y tg α > 0 en todos los csos. sen α 0,9 cos α 0, 9 0,9 tg α cos α 0, sen α 0, 0,99 tg α tg α 0,7 sen cos sen 07, 8 sen 07, cos + cos 09,,6 09, 099, 8, 0, (0,7 cos α) + cos α 0,6cos α + cos α,6cos α cos α sen α 0,7 cos α sen α 0,6 cos α 0,8, 6 sen α cos α tg α 9 9 cos α sen α 7 7 tg α 9 9 tg α sen cos sen 8 sen cos + cos / / 7/ 7 / ( cos α) + cos α cos α + cos α cos α sen α cos α sen α cos α cos α
22 Por tnto: sen α 0,9 0,99 0,6 / 7 / / cos α 0,9 0, 0,8 / / / tg α,6 8, 0,7 / / 8. lcul el vlor de ls siguientes epresiones sin utilizr l clculdor: ) sen cos b) sen 0 + cos 60 c) sen 0 + cos 0 d) tg 0 + tg 60 e) tg cos 60 f) tg + sen ) sen cos 0 b) sen 0 + cos 60 + c) sen 0 + cos d) tg 0 + tg 60 + e) tg cos 60 f) tg + sen + + lculdor 9. omplet en tu cuderno l tbl siguiente, utilizndo l clculdor: α 0' 7 ' 0'' 8, sen α 0,6 0,8 0,9 0,997 cos α 0,97 0,7 0,0 0,078 tg α 0,7,,6,7 0. Hll el ángulo α < 90 en cd cso. Epréslo en grdos, minutos y segundos. ) sen α 0,8 b) cos α 0,7 c) tg α, d) sen α e) cos α f ) tg α ) α 7' " b) α ' " c) α 68 ' " d) α 8 ' " e) α ' 8" f) α 76 ' ". Hll, con l clculdor, ls otrs rzones trigonométrics del ángulo α < 90 en cd uno de los csos siguientes: ) sen α 0, b) cos α 0,7 c) tg α,7 d) sen α e) tg α f ) cos α ) cos α 0,97; tg α 0, b) sen α 0,67; tg α 0,9 c) sen α 0,87; cos α 0, d) cos α 0,7; tg α e) sen α 0,87; cos α 0, f) sen α 0,; tg α 0,8
23 Resolución de triángulos. Resuelve los siguientes triángulos rectángulos (^ 90 ) hllndo l medid de todos los elementos desconocidos: ) cm, b cm. Hll c, ^, ^. b) m, ^ 7. Hll b, c, ^. c) 7 m, ^ 8. Hll b, c, ^. d) c,8 km, ^ 7. Hll, b, ^. ) Por el teorem de Pitágors: c cm c + c 69 c cm tg ^ ^ 7' " b cm ^ 90 ^ ^ 67 ' 9" b) ^ 90 ^ ^ sen 7 c c sen 7 c m c 7, m tg 7 b b tg 7 7 b 7,06 m b c) ^ 90 ^ c b 8 7 m tg 8 b 7 ^ b 7 tg 8 b,0 m cos 8 7 c 7 c cos 8 c, m d) ^ 90 ^ ^ 9 c,8 km sen 7 cos 7 8, b 8,,8 sen 7,8 km b,8 cos 7 b,89 km 7 b
24 . undo los ryos del sol formn 0 con el suelo, l sombr de un árbol mide 8 m. uál es su ltur? 0 8 m tg 0 8 El árbol mide, m.. Un escler de m está poyd en un pred. Qué ángulo form l escler con el suelo si su bse está, m de l pred? m cos α, 0, α 66 ' 9", m
25 Págin 9. lcul el perímetro y el áre de un triángulo isósceles en el que el ángulo desigul mide 7 y l medid del ldo opuesto ese ángulo es de 6 m. 7 ^ m 8 m cos 8 8 8,6 m cos Perímetro,6 + 6, m ltur, h: tg 8 h h 8 tg,0 m Áre 6, 0 88, m 6. Un mástil está sujeto tierr con dos cbles de m que formn ángulos de 0 con el suelo. lcul l ltur del mástil y l distnci de l bse los puntos de sujeción. M m m 0 0 d d sen 0 cos 0 d sen 0 9,9 m d cos 0 d 7,7 m El mástil mide 9,9 m y l distnci de l bse del mástil los puntos de sujeción y es 7,7 m. 7. lcul l ltur, h, y el áre de los siguientes triángulos: 8 cm h h 8 cm 6 D cm D cm sen 6 h h 6, cm sen h h 6, cm 8 8 6, 60,8 cm 6, 0,6 cm 8. Pr medir l ltur de un árbol, nos situmos 0 m de su bse y observmos, desde el suelo, su prte más lt bjo un ángulo de 0. uánto mide el árbol? h 0 0 m tg 0 h h 0 tg 0,8 m 0
26 9. Un comet está sujet l suelo medinte un hilo que mide 0 m y que form con l horizontl un ángulo de 60. qué ltur está l comet? OMET sen 60 h h 0 sen 60 h m 60 h h m L comet está un ltur de m. Rzones trigonométrics de ángulos culesquier 0. Sitú en l circunferenci goniométric los siguientes ángulos e indic el signo de sus rzones trigonométrics. ) 8 b) 98 c) 87 d) 98 e) 8 f ) 0 ompruéblo con l clculdor. ) 8 b) 8 sen + cos tg sen cos tg + c) 87 d) 87 sen + cos + tg sen + cos tg e) 8 f) 8 sen cos + tg 0 0 sen cos + tg. Eplic en qué cudrnte está el ángulo α en cd cso y clcul ls rzones trigonométrics que fltn: ) sen α 0,6; cos α < 0 b) cos α /; tg α > 0 c) tg α ; sen α > 0 d) sen α /; tg α < 0 Represent el ángulo α en un circunferenci goniométric en cd cso. ) sen 06, > 0 8 é IoII cudrnte α II cudrnte cos < 0 8 éii oiii cudrnte sen α + cos α cos α sen α cos α 0,6 cos α 0,6 tg α sen tg α cos cos α 06, cos α 0,8 06, 08, tg α 0,7 6
27 Representción de α en un circunferenci goniométric: 6 ' " sen α 0,6 α ) 78 ' " sen cos α II cudrnte α 7' 8" b) cos < 0 8 éii o IIIcudrnte α III cudrnte tg > 0 8 éioiiicudrnte sen α + cos α sen α cos α sen α c m sen α 8 9 tg α sen α 8 sen α 9 sen tg α 8 tg cos Representción de α en l circunferenci goniométric: cos α α 09 8' 6" ) 0 ' " α III cudrnte α 0 ' " cos sen c) tg < 0 8 éiioiv cudrnte α II cudrnte sen > 0 8 éioii cudrnte sen cos sen + cos 8 sen cos ( cos α) + cos α cos α + cos α cos α cos α sen α cos α sen α cos α 7
28 Representción de α en l circunferenci goniométric: 6 ' " tg α α ) 96 ' " tg α II cudrnte α 6 ' " sen cos d) sen < 0 8 éiii oiv cudrnte α IV cudrnte tg < 0 8 éii oiv cudrnte sen α + cos α cos α sen α cos α c m tg α sen tg α cos cos α 9 cos α tg α Representción de α en l circunferenci goniométric: sen α α 8 ' " ) 8' 7" cos sen α IV cudrnte α 8 ' ". Justific en qué cudrnte está α, en cd cso, y clcul ls restntes rzones trigonométrics: ) sen α /; α < 90 b) cos α /; α > 70 c) tg α ; α >80 d) cos α /; α < 80 ) sen α, α < 90 α I cudrnte y cos α > 0 sen α + cos α cos α tg α sen tg α cos / / c m cos α 9 cos α 9 8
29 b) cos α, α > 70 α IV cudrnte y sen α < 0 sen α + cos α sen α c m sen α sen α 9 9 tg α sen tg α cos c) tg α, α > 80 α III cudrnte sen cos sen + cos 8 sen cos (cos α) + cos α 9cos α + cos α 0cos α cos α 0 cos α 0 0 sen α cos α sen α d) cos α, α < 80 α II cudrnte y sen α > 0 sen α + cos α sen α cos α sen α c m tg α sen tg α cos plic lo prendido. Hll: ) L longitud. b) El áre del triángulo. ) En sen α 7 sen α & D, cos D 8 D, 8 cm En D &, cos D 8 D 9 cm b) Hllmos l ltur h en el triángulo D: 7 cm D,8 + 9,8 cm h cm sen h h 8,7 cm bc h, 8 8, 7 9,9 cm 9
30 . El ldo de un rombo mide 8 cm y el ángulo menor es de 8. uánto miden ls digonles del rombo? sen 9 y 8 y 8 sen 9 y,60 cm y 8 cm 9 Digonl menor y,0 cm cos 9 8 cos 9 7,6 cm 8 Digonl myor, cm. Hll el áre de un prlelogrmo cuyos ldos miden 6 cm y cm y formn un ángulo de 0. 6 cm 0 h cm sen 0 h h 6 sen 0 h 0,8 cm 6 Áre 0,8 6,7 cm 6. En un crreter de montñ, un señl indic un ltitud de 78 m. Tres kilómetros más delnte, l ltitud es de 06 m. Hll l pendiente medi de l crreter y el ángulo que form con l horizontl. α 000 m m sen α 80 sen α 7 α ' 9" tg α 0,09 pendiente 9, % 7. ) En el triángulo, rectángulo en, clcul H y H. b) Hll ls rzones trigonométrics del ángulo ^ en el triángulo y en el triángulo H y comprueb que coinciden. 7 cm H cm cm ) Por el teorem del cteto: H 8 H 8 H,0 cm Por el teorem de Pitágors: H,0 H, 0 8 H 6,7 cm b) Rzones trigonométrics de ^ sen ^ cos ^ tg ^ H H H H 67, 0,8, 0 0,96 67, 0,9, 0 en H & : 0
31 Rzones trigonométrics de ^ en & : sen ^ cos ^ 7 0,8 0,96 tg ^ 7 0,9 8. Hll, en cd triángulo, l ltur y el ldo desconocido: ) b) 8 cm h 6 P cm 7 cm 9 cm h 0 P y ) En el triángulo P : sen 6 h h 6, cm 8 cos 6 P 8 8 P 7,6 P P 7,6,9 + P 6, +, 9, cm h b) En el triángulo P : cos 0 7 0,9 cm sen 0 h h,0 cm 7 En el triángulo P : y 9 h 9, 0,9 cm + y 6,8 cm 9. En un circunferenci de rdio 6 cm trzmos un cuerd cm del centro O. % Hll el ángulo O. M O O 6 cm; OM cm O cos 8 cos % α O 0
32 0. ) Epres en rdines los ángulos de 0,, 60 y 90 prtir de l equivlenci 80 π rd. b) Epres en rdines los siguientes ángulos teniendo en cuent que son múltiplos de los nteriores: 0 ; ; 0 ; 00 y 70. ) 0 0π 80 π 80 rd π rd b) rd π rd 60 60π rd π rd 0 60 π rd π 80 rd π rd π 6 π rd rd π rd π rd
33 Págin 60. Epres en grdos los siguientes ángulos ddos en rdines: Teniendo en cuent que π rd 80 : π ; π ; π ; 7π ; π; π 6 9 π rd 80 0 π rd π rd 80 7π rd π rd 80 0 π rd ) En un circunferenci de 8 cm de rdio, dibujmos un ángulo de, rdines. Qué longitud tendrá el rco correspondiente? b) Si en l mism circunferenci, un rco mide cm, hll l medid del ángulo centrl en grdos y en rdines. ) Sbemos que si un ángulo mide rd entonces el rco correspondiente tendrá un longitud igul l rdio, por tnto, un ángulo de, rd le corresponde un rco cuy longitud es, veces el rdio. En nuestro cso: Longitud del rco α r, 8 0 cm b) Longitud delrco cm Rdio 8cm Longitud delrco 8 rd, r 8 rd 80 π rd, rd 8, ' " π Resuelve problems. Desde el punto donde estoy, l visul l punto más lto del edificio que tengo en frente form un ángulo de 8 con l horizontl. Si me cerco 0 m, el ángulo es de 0. uál es l ltur del edificio? 8 0 m 0 h tg tg 0 8 h h 0 + h tg 0 h tg 8 ( 0 + ) tg 0 tg 8 (0 + ) tg 0 0 tg 8 + tg 8 (tg 0 tg 8 ) 0 tg 8 h tg 0 h 9,0 m Por tnto, el edificio mide 9,0 m. 0 tg 8,9 m tg 0 tg 8
34 . Dos edificios distn entre sí 90 m. Desde un punto que está entre los dos edificios vemos que ls visules los puntos más ltos de estos formn con l horizontl ángulos de y 0. uál es l ltur de los edificios si sbemos que uno es 6 m más lto que el otro? Primer solución: el edificio es más lto que el. EDIFIIO EDIFIIO h m h tg h + 6 h tg 6 8 tg 6 tg 0 (90 ) tg 0 h h tg 0 ( 90 ) 90 tg 6 90 tg 0 tg 0 tg + tg 0 90 tg (tg + tg 0 ) 90 tg tg tg + tg 0 6, m h tg 6 h 9,0 m ltur del edificio h + 6,0 m ltur del edificio h 9,0 m Segund solución: el edificio es más lto que el. EDIFIIO EDIFIIO h 0 90 m 90 h + 6 tg h h tg 8 tg 0 (90 ) tg + 6 tg 0 h + 6 tg 0 ( 90 ) h tg 0 tg 0 tg tg 0 6 (tg + tg 0 ) 90 tg 0 6 tg + tg 0, m h tg h 7,60 m ltur del edificio h 7,60 m ltur del edificio h + 6,60 m
35 . Un vión P vuel entre dos ciuddes y que distn entre sí 0 km. Desde el % % vión se miden los ángulos P 0 y P 0. qué ltur está el vión? P h 0 0 km 0 0 tg tg 0 h h tg 0 8 tg 0 tg 0 (0 ) 0 h h tg 0 ( 0 ) 0 tg 0 0 tg 0 tg 0 0 tg 0 tg 0 + tg 0 0,67 km h tg 0 h,6 km Por tnto, el vión vuel,6 km de ltur. 6. En lo lto de un edificio en construcción hy un grú de m. Desde un punto del suelo se ve el punto más lto de l grú bjo un ángulo de con respecto l horizontl y el punto más lto del edificio bjo un ángulo de 0 con l horizontl. lcul l ltur del edificio. GRÚ m h 0 tg tg 0 h h tg 0 8 tg 0 tg h + h tg (tg tg 0 ),86 m tg tg 0 h tg 0 h 0,86 m Por tnto, el edificio mide 0,86 m de ltur.
36 7. Pr clculr l ltur del edificio, PQ, hemos medido los ángulos que indic l figur. Sbemos que hy un funiculr pr ir de S Q, cuy longitud es de 0 m. Hll PQ. P Q 0 0 m S 0 R lculmos SR RQ sen y RQ en el triángulo SRQ & : RQ 0 sen 0 RQ m cos 0 SR 8 SR 0 cos SR m & lculmos RP en el triángulo SPR : tg 0 RP 8 8 8, SR tg 0 RP RP tg 0 RP 8 67 m Luego PQ RP RQ 8,67 m m 6,67 m Por tnto, l ltur del edificio es de 6,67 m. 8. Pr loclizr un emisor clndestin, dos receptores, y, que distn entre sí 0 km, orientn sus ntens hci el punto donde está l emisor. E Ests direcciones formn con ángulos de 0 y 6. qué distnci de y se encuentr l emisor? 0 0 km 6 tg tg 6 0 y y tg 6 8 y y tg 0 ( 0 ) 0 y E tg 6 tg 0 (0 ) tg 6 0 tg 0 tg 0 (tg 6 + tg 0 ) 0 tg 0 0 tg 0 tg 6 + tg 0,8 km y tg 6 y 6,0 km onocidos e y podemos hllr ls distncis de y l emisor. sen 0 sen 6 y E y E 8 y E sen 0 8 E 9,8 km 8 y E sen 6 8 E 6,6 km Por tnto, l emisor se encuentr 9,8 km de y 6,6 km de. 6
37 9. Desde un cntildo 0 m sobre el nivel del mr, se observ un helicóptero en práctics de slvmento. Un person desciende verticlmente hst un brco en el que lguien está en peligro. Si los ángulos de observción son de 7 pr el helicóptero y 8 pr el brco, cuánto medirá el cble que v desde el helicóptero l brco? En el triángulo PQ tg PQ,6 m PQ m P 7 8 Q 0 m Q En el triángulo PQ tg 7 8 PQ Longitud del cble 9, + 0, m Q,6 tg 7 9, m 0. En un trpecio isósceles de bses y D, conocemos los ldos m y m, y los ángulos que form l bse myor con los ldos oblicuos, que son de. Hll su áre. m m h D Áre ( + ) m sen h h m cos m se myor + + m. Desde un fro F se observ un brco bjo un ángulo de con respecto l líne de l cost; y un brco, bjo un ángulo de. El brco está km de l cost, y el, km. lcul l distnci entre los brcos. lculmos F sen sen F F 8 8 y F : F 7, km sen F 8,7 km sen Pr clculr d utilizmos el triángulo de l derech: sen h 7, h 7, sen,7 km cos 7, 7, cos 6,8 km y 8,7 y 8,7 6,8,7 km F F 7, km 8,7 km Utilizmos el teorem de Pitágors: d + y 7, +, 7,6 km L distnci entre y es de,6 km. h d km km h y d 7
38 . Pr iluminr un prcel rectngulr se hn colocdo tres focos en P de modo que los ángulos de iluminción P %, P % y PD % son igules. 0 m P D Un verí pg el foco centrl. uál es el áre y el perímetro de l zon oscurecid, si P 0 m? 0 m P D En el triángulo P tg En el triángulo P tg En el triángulo P cos P P 8,9 m 86,6 m 00 m Áre rectángulo 0 86, 6 0 m Áre Áre P 8, 9 0 7, m PD 86, m Áre de P: 0 ( 7, + 6), m lculmos hor el perímetro de P : En P, cos P 7, 7 m P 86, 6 89, 7, 7 m Perímetrode P: P + + P, m 8
39 Págin 6. En l prcel D conocemos ^ D^ 90 ; ^ 0 ; D 8 m y 9 m. Queremos verigur l longitud de l digonl. 9 m 8 m D Un migo topógrfo nos sugiere prolongr los ldos y D hst que se corten en % un punto P y verigur cuánto mide el ángulo PD. Hzlo tú. 9 m 0 8 m 60 0 P D % PD % PD En el triángulo PD, sen 0 8 P 8 P 6 m P m En el triángulo P : tg , m En el triángulo 9 + 7, 7, m Problems +. Sobre l circunferenci goniométric señlmos un ángulo α en el primer cudrnte y prtir de él dibujmos los ángulos: usc l relción que eistre entre: 80 α 80 + α 60 α ) sen (80 α) y sen α b) sen (80 + α) y sen α c) sen (60 α) y sen α cos (80 α) y cos α cos (80 + α) y cos α cos (60 α) y cos α tg (80 α) y tg α tg (80 + α) y tg α tg (60 α) y tg α 80 α α 80 + α α 60 α α ) sen (80 α) sen α b) sen (80 + α) sen α c) sen (60 α) sen α cos (80 α) cos α cos (80 + α) cos α cos (60 α) cos α tg (80 α) tg α tg (80 + α) tg α tg (60 α) tg α 9
40 . Sitú el ángulo ddo sobre l circunferenci goniométric y epres sus rzones trigonométrics utilizndo un ángulo gudo como en el ejemplo: Ángulo: sen sen cos cos tg tg ) 0 b) 0 c) 00 d) e) 00 f ) 0 ) sen 0 sen 0 b) sen 0 sen 60 c) sen 00 sen 60 cos 0 cos 0 cos 0 cos 60 cos 00 cos 60 tg 0 tg 0 tg 0 tg 60 tg 00 tg d) sen sen e) sen 00 sen 80 f) sen 0 sen 0 cos cos cos 00 cos 80 cos 0 cos 0 tg tg tg 00 tg 80 tg 0 tg Hll los ángulos comprendidos entre 0 y 60 que verificn ls siguientes ecuciones, como en el ejemplo: cos 0 cos / 60 ; 00 ) sen b) sen c) tg + 0 d) (sen ) e) (sen ) sen 0 f ) (sen ) 0 g) (cos ) cos 0 60 ) sen sen ) b) sen sen ) 0
41 c) tg + 0 tg tg ) 90 d) sen sen ± sen ) sen e) (sen ) sen 0 sen (sen ) 0 0 sen 0 ) sen 0 sen 90 f) (sen ) 0 sen sen sen ± sen 0 ) sen 0 ) 0 0 0
42 g) (cos ) cos 0 Efectumos el cmbio de vrible cos t t t 0 t ± + 8 ± Deshcemos el cmbio de vrible: t t / t cos t cos 0 ) Usndo ls relciones fundmentles, demuestr ests igulddes: ) (sen α + cos α) + (sen α cos α) b) ( sen ) + sen ( cos ) sen c) ( sen ) + sen ( cos ) cos d) + ( tg ) ( cos ) tg ) (sen α + cos α) + (sen α cos α) (sen α + cos α + sen α cos α) + (sen α + cos α sen α cos α) + sen α cos α + sen α cos α b) sen + sen cos sen ( sen + cos ) sen sen sen α + cos α c) sen + sen cos sen ( sen + cos ) sen cos cos cos sen tg α cos d) + tg α + sen cos + sen cos cos cos
43 Refleion sobre l teorí 8. Verddero o flso? Justific y pon ejemplos. ) En un ángulo gudo, el seno es siempre myor que l tngente. b) No eiste ningún ángulo α tl que sen α / y tg α /. c) El coseno de un ángulo de π rdines es igul. d) El vlor máimo de l tngente de un ángulo es. e) Si 70 < α < 60, entonces tg α < 0 y cos α > 0. f ) No eiste ningún ángulo α tl que: sen α + cos α 0 g) L ltur de un triángulo es igul l producto de uno de sus ldos por el seno del ángulo que form dicho ldo con l bse. ) Flso, por ejemplo, sen < tg. b) Verddero. Si sen α y tg α entonces: tg α c) Verddero. sen 8 cos sen 8 cos cos, imposible. tg d) Flso, l tngente de un ángulo puede tomr culquier vlor rel. e) Verddero. f) Flso: sen α + cos α 0 sen α cos α tg α sen cos 6 ' " ) 96 ' " g) Verddero. α h sen α h 8 h sen α 9. Los dos ángulos gudos de un triángulo rectángulo se llmn complementrios porque su sum es uno recto. Observ l figur, copi y complet l tbl, y epres simbólicmente lo que obtienes: c α 90 α b α 90 α sen b/ c/ cos c/ b/ tg b/c c/b sen α cos (90 α) cos α sen (90 α) tg α tg ( 90 )
44 Págin 6 Entrénte resolviendo problems Qué frcción de l superficie del triángulo se h coloredo? m m Los triángulos & y DE & están en posición de Tles, son semejntes y l rzón de semejnz es Si l rzón de semejnz es : D m. m Áre DE & Áre & Áre & FE Áre G & Por tnto: m m D F G E Áre FEG & Áre G & Áre & FE Áre G & Áre G & Áre G & < & & Áre F Áre 8 El rombo tiene un superficie de cm, y su digonl menor es igul los tres curtos de l myor. lcul el áre del círculo inscrito. r En primer lugr hllremos l longitud de ls digonles y del ldo del rombo. Digonl myor Digonl menor 8 c m cm Áre rombo cm
45 Luego: Digonl myor 8 cm; Digonl menor 6 cm l Por el teorem de Pitágors: l + l cm Por tnto, el ldo del rombo mide cm. hor hllremos l longitud del rdio del círculo. El círculo es tngente l rombo en D D, es decir, D es l ltur sobre l hipotenus del triángulo rectángulo & y divide este en otros dos triángulos rectángulos, r D D & y D &. En En & ì : sen D & : sen ì D D 8 D, cm El rdio del círculo es D, cm. Finlmente hllmos el áre del círculo: Áre π,,76π cm 8,09 cm Infórmte Eclipses omplet en tu cuderno los dtos que fltn en l tbl, y comprueb que el ángulo β es similr si se clcul prtir de los dtos reltivos l Lun o de los reltivos l Sol. diámetro (km) distnci medi l tierr (km) tg α lun ?? sol ?? β lun: Diámetro 00 km R 70 km tg α sol: 0,007 α 0 ' 0" β α 0 ' 0" Diámetro R' tg α ,00676 α 0 6' " β 0 ' 9" diámetro (km) distnci medi l tierr (km) tg α lun ,007 0 ' 0" sol , ' 9" β
46 Págin 6 utoevlución. ) Si cos α 0, y α < 90, clcul sen α y tg α. b) Si tg β y β < 90, clcul sen β y cos β. ) sen α ( cos ) 0, 0,8; tg α 0,8/0,,6 sen b b ( / ) cos b b) tg b sen cos b ( cos b) ( cos b) 8 69 ( cos b) 8 ( sen b) ( cos b) + + (cos β) cos β 69 cos β 8 sen b. Los brzos de un compás, que miden cm, formn un ángulo de 0. uál es el rdio de l circunferenci que puede trzrse con es bertur? sen,07 cm 0 cm Rdio de l circunferenci 0, cm. Pr medir l nchur de un río, hemos tomdo ls medids indicds en l figur. Hálll. 6 y 0 tg 6 y tg y 0 y tg 6 y (0 ) tg 6 0 m tg 6 (0 ) tg y tg 6 8 m El río tiene 8 m de nchur. 0 tg tg 6 + tg 8,89 6
47 . En este triángulo, hll l ltur sobre, el áre del triángulo y el ángulo ^. 7 m 68 8 m ltur sobre h sen 68 h h,76 m 7 Áre del triángulo 8, 76 0,6 m cos m 68 h 8 tg ^ 6,7 m; 8,6 m h 0,79 ^ 6 ' " 6 8. En un huerto hy un pozo de, m de ncho. undo está vcío vemos, desde el brocl, el borde opuesto del fondo bjo un ángulo de 70 con l horizontl. undo el gu sube, vemos el borde opuesto del gu bjo un ángulo de. uál es l ltur del pozo? uánto subió el gu? P En el triángulo P tg 70 P, 8 P, m D En el triángulo PD tg PD, 8 PD, m ltur del pozo: P, m 70, m ltur del gu: P PD,,, m 6. Si cos α / y tg α < 0, indic en qué cudrnte está el ángulo α y clcul sus restntes rzones trigonométrics. cos < 0 8 é IIoIII cudrnte α II cudrnte tg < 0 8 éii oivcudrnte sen α + cos α sen α cos α sen α c m sen α sen α sen α 6 tg α sen tg α cos 6 tg α 6 Por tnto, sen α 6, cos α y tg α 6. 7
1 Halla las razones trigonométricas del ángulo a en cada uno de estos triángulos: a) b) c)
 Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
7Soluciones a los ejercicios y problemas PÁGINA 161
 7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
BLOQUE III Geometría
 LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
Resolución de triángulos
 8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
Trigonometría I. 1. Ángulos. página Razones trigonométricas de un ángulo agudo. página 70
 Trigonometrí I E S Q U E M D E L U N I D D.. Ángulo en el plno págin 67. Ángulos págin 67.. riterio de orientción de ángulos págin 67.. Sistems de medid de ángulos págin 67.4. Reducción de ángulos l primer
Trigonometrí I E S Q U E M D E L U N I D D.. Ángulo en el plno págin 67. Ángulos págin 67.. riterio de orientción de ángulos págin 67.. Sistems de medid de ángulos págin 67.4. Reducción de ángulos l primer
11. Triángulos SOLUCIONARIO 1. CONSTRUCCIÓN DE TRIÁNGULOS 2. MEDIANAS Y ALTURAS DE UN TRIÁNGULO
 SLUINRI 95 11. Triángulos 1. NSTRUIÓN DE TRIÁNULS PIENS Y LUL Justific si se pueden dibujr los siguientes triángulos conociendo los dtos: ) Tres ldos cuys longitudes son 1 cm, 2 cm y 3 cm b) Un ldo de
SLUINRI 95 11. Triángulos 1. NSTRUIÓN DE TRIÁNULS PIENS Y LUL Justific si se pueden dibujr los siguientes triángulos conociendo los dtos: ) Tres ldos cuys longitudes son 1 cm, 2 cm y 3 cm b) Un ldo de
REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS
 TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
1.6 Perímetros y áreas
 3 1.6 Perímetros y áres Perímetro: es l medid del contorno de un figur. Superficie (pln): es el conjunto de puntos del plno encerrdos por un figur geométric pln. Áre: es l medid de un superficie. Represente
3 1.6 Perímetros y áres Perímetro: es l medid del contorno de un figur. Superficie (pln): es el conjunto de puntos del plno encerrdos por un figur geométric pln. Áre: es l medid de un superficie. Represente
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Clasifica los siguientes polígonos. a) b) c) d)
 1 FIGURS PLNS EJERIIS PR ENTRENRSE Polígonos 1.44 lsific los siguientes polígonos. ) b) c) d) ) Pentágono irregulr cóncvo. b) Heptágono regulr convexo. c) ctógono irregulr cóncvo. d) Hexágono irregulr
1 FIGURS PLNS EJERIIS PR ENTRENRSE Polígonos 1.44 lsific los siguientes polígonos. ) b) c) d) ) Pentágono irregulr cóncvo. b) Heptágono regulr convexo. c) ctógono irregulr cóncvo. d) Hexágono irregulr
Senx a) 0 b) 1 c) 2 d) 2
 EJERIIOS. lculr en : Sen( - 0º) = os( + 0º) ) b) c) 4 d) 6 e). Si : Tg (8 º) Tg ( + º) = Hllr: K = Sen tg 6 7 7 ) b) c) - d) - e) ) 0, b) c), d) e) 8. Si : Tg =, Sen lculr : K Tg ) c) e) ( ) b) d) ( ).
EJERIIOS. lculr en : Sen( - 0º) = os( + 0º) ) b) c) 4 d) 6 e). Si : Tg (8 º) Tg ( + º) = Hllr: K = Sen tg 6 7 7 ) b) c) - d) - e) ) 0, b) c), d) e) 8. Si : Tg =, Sen lculr : K Tg ) c) e) ( ) b) d) ( ).
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Razones trigonométricas
 LECCIÓ CODESADA 12.1 Rzones trigonométrics En est lección Conocerás ls rzones trigonométrics seno, coseno y tngente Usrás ls rzones trigonométrics pr encontrr ls longitudes lterles desconocids en triángulos
LECCIÓ CODESADA 12.1 Rzones trigonométrics En est lección Conocerás ls rzones trigonométrics seno, coseno y tngente Usrás ls rzones trigonométrics pr encontrr ls longitudes lterles desconocids en triángulos
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGIN 13 EJERCICIOS Operciones con ángulos y tiempos 1 Efectú ls siguientes operciones: ) 7 31' 15" 43 4' 57" b) 163 15' 43" 96 37' 51" c) (37 4' 19") 4 d) (143 11' 56") : 11 ) 7 31' 15" 43 4' 57"
Pág. 1 PÁGIN 13 EJERCICIOS Operciones con ángulos y tiempos 1 Efectú ls siguientes operciones: ) 7 31' 15" 43 4' 57" b) 163 15' 43" 96 37' 51" c) (37 4' 19") 4 d) (143 11' 56") : 11 ) 7 31' 15" 43 4' 57"
EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES 2º PARCIAL
 Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
PROBLEMAS DE OPTIMIZACIÓN
 PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
Semejanza. 2. Relación entre perímetros, áreas y volúmenes de figuras semejantes 51
 Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
Trigonometría: ángulos / triángulos. matemática / arquitectura
 Trigonometrí: ángulos / triángulos mtemátic / rquitectur Grn pirámide de Guiz. Egipto. 2750.C. (h=146,62m / l=230,35m) Pirámide del Museo Louvre. Pris. 1989. rq. Ieoh Ming Pei. (h=20m / l=35m) Grn pirámide
Trigonometrí: ángulos / triángulos mtemátic / rquitectur Grn pirámide de Guiz. Egipto. 2750.C. (h=146,62m / l=230,35m) Pirámide del Museo Louvre. Pris. 1989. rq. Ieoh Ming Pei. (h=20m / l=35m) Grn pirámide
Los polígonos y la circunferencia
 l: ldo 12 Los polígonos y l circunferenci 1. Polígonos lcul cuánto mide el ángulo centrl mrcdo en los siguientes polígonos: P I E N S Y L U L R l: ldo R R? R? R R? R R? R E l: ldo l: ldo F E 360 : 3 =
l: ldo 12 Los polígonos y l circunferenci 1. Polígonos lcul cuánto mide el ángulo centrl mrcdo en los siguientes polígonos: P I E N S Y L U L R l: ldo R R? R? R R? R R? R E l: ldo l: ldo F E 360 : 3 =
TEMA 1. NÚMEROS REALES
 TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
2.- Dos ángulos de un triángulo miden 73º y 58º respectivamente. Determina el ángulo que forman sus bisectrices.
 GEOMETRÍ 1.- Determin ls medids de los ángulos desconocidos. ) b) " 31º " 20º 47º 2.- Dos ángulos de un triángulo miden 73º y 58º respectivmente. Determin el ángulo que formn sus bisectrices. 3.- uánto
GEOMETRÍ 1.- Determin ls medids de los ángulos desconocidos. ) b) " 31º " 20º 47º 2.- Dos ángulos de un triángulo miden 73º y 58º respectivmente. Determin el ángulo que formn sus bisectrices. 3.- uánto
3. Expresa los siguientes radicales mediante potencias de exponente fraccionario y simplifica: 625 d) 0, 25 e) c) ( ) 4 8
 POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
SOLUCIONARIO 1. PERÍMETROS Y ÁREAS DE LOS POLÍGONOS (I) 4. Calcula el área de un triángulo rectángulo en el que los catetos miden 22 m y 16 m
 11 elige Mtemátics, curso y tem. 13. Perímetros y áres 4. Clcul el áre de un triángulo rectángulo en el que los ctetos miden m y 16 m 1. PERÍMETROS Y ÁREAS DE LOS POLÍGONOS (I) PIENSA Y CALCULA Hll mentlmente
11 elige Mtemátics, curso y tem. 13. Perímetros y áres 4. Clcul el áre de un triángulo rectángulo en el que los ctetos miden m y 16 m 1. PERÍMETROS Y ÁREAS DE LOS POLÍGONOS (I) PIENSA Y CALCULA Hll mentlmente
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
( )( ) 0 1,1 1, 5 2 2, 3. 1 Resuelve las siguientes inecuaciones: a) 2x + 4 > x +6 b) - x + 1 < 2x + 4 c) x + 51 > 15x + 9
 1 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 < x + 4 c) x + 51 > 15x + 9 x < x > -1 c) x < 4 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 > x + 4 c) 5x + 10 < 1x - 4 x > x < -
1 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 < x + 4 c) x + 51 > 15x + 9 x < x > -1 c) x < 4 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 > x + 4 c) 5x + 10 < 1x - 4 x > x < -
FUNCIONES. Analíticamente, la correspondencia anterior se escribe del modo siguiente:
 FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
EJERCICIOS DE GEOMETRÍA
 VECTORES EJERCICIOS DE GEOMETRÍA 1. Hllr un vector unitrio u r r r r de l mism dirección que el vector v = 8i 6j.Clculr otro vector ortogonl v r y de módulo 5.. Normliz los vectores: u r = ( 1, v r = (-4,3
VECTORES EJERCICIOS DE GEOMETRÍA 1. Hllr un vector unitrio u r r r r de l mism dirección que el vector v = 8i 6j.Clculr otro vector ortogonl v r y de módulo 5.. Normliz los vectores: u r = ( 1, v r = (-4,3
Se traza la paralela al lado a y distancia la altura h a.
 Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
10.- Teoremas de Adición.
 Trigonometrí 10.- Teorems de Adición. Rzones trigonométrics de los ángulos A + B y A B. Hy que tener cuiddo de no confundir l rzón trigonométric de l sum de dos ángulos, con l sum de dos rzones trigonométrics.
Trigonometrí 10.- Teorems de Adición. Rzones trigonométrics de los ángulos A + B y A B. Hy que tener cuiddo de no confundir l rzón trigonométric de l sum de dos ángulos, con l sum de dos rzones trigonométrics.
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
11 Perímetros y áreas de figuras planas
 86464 _ 0371-0384.qxd 1//07 09:4 Págin 371 Perímetros y áres de figurs plns INTRODUCCIÓN En est unidd repsmos ls uniddes de longitud y superficie. Se introducen tmbién lguns uniddes de medid del sistem
86464 _ 0371-0384.qxd 1//07 09:4 Págin 371 Perímetros y áres de figurs plns INTRODUCCIÓN En est unidd repsmos ls uniddes de longitud y superficie. Se introducen tmbién lguns uniddes de medid del sistem
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
POLIEDROS - PRISMAS POLIEDRO. I. POLIEDRO: es el sólido limitado por cuatro o más regiones poligonales llamados caras.
 POIROS - PRISMS POIRO I. POIRO: es el sólido limitdo por cutro o más regiones poligonles llmdos crs. RIST TR TUR RIST SI PRISM VRTI S R 1. PRISM: l prism es un poliedro cuys crs lterles son tres o más
POIROS - PRISMS POIRO I. POIRO: es el sólido limitdo por cutro o más regiones poligonles llmdos crs. RIST TR TUR RIST SI PRISM VRTI S R 1. PRISM: l prism es un poliedro cuys crs lterles son tres o más
LA FUNCIÓN LOGARÍTMICA
 LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA 7: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS
 TEMA 7: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS. POTENCIAS L epresión n se llm potenci de bse y eponente n: Si n es un número nturl: n =, n veces. 0 =, = n m n n m = y = n Ejercicios: º)
TEMA 7: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS. POTENCIAS L epresión n se llm potenci de bse y eponente n: Si n es un número nturl: n =, n veces. 0 =, = n m n n m = y = n Ejercicios: º)
LA RECTA DEL PLANO P O L I T E C N I C O 1 ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS
 L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 06 EJERCICIOS Tipos de poliedros 1 Di, justificdmente, qué tipo de poliedro es cd uno de los siguientes: A B C D E Hy entre ellos lgún poliedro regulr? A Prism pentgonl recto. Su bse es un
Pág. 1 PÁGINA 06 EJERCICIOS Tipos de poliedros 1 Di, justificdmente, qué tipo de poliedro es cd uno de los siguientes: A B C D E Hy entre ellos lgún poliedro regulr? A Prism pentgonl recto. Su bse es un
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 4: Lunes 1 - Viernes 5 de Abril. Contenidos
 Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
INSTITUTO POLITECNICO NACIONAL CECYT MIGUEL BERNARD PERALES GUIA DE GEOMETRIA ANALITICA
 INSTITUTO POLITECNICO NACIONAL CECYT MIGUEL BERNARD PERALES GUIA DE GEOMETRIA ANALITICA I. LA RECTA. Ejercicios pr resolver. 1. Demuestr que los puntos A(-,8); B(-6,1) C(0,4) son los vértices de un tringulo
INSTITUTO POLITECNICO NACIONAL CECYT MIGUEL BERNARD PERALES GUIA DE GEOMETRIA ANALITICA I. LA RECTA. Ejercicios pr resolver. 1. Demuestr que los puntos A(-,8); B(-6,1) C(0,4) son los vértices de un tringulo
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA. Capítulo SISTEMA DE COORDENADAS. Demostrar que los puntos A = ( 0,1) son los vértices de un cuadrado.
 PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA Cpítulo SISTEMA DE COORDENADAS Demostrr que los puntos A ( 0,) B (,5) ; C ( 7,) D (, ) son los vértices de un cudrdo. Solución AB 9 6 5 5 BC 6 9 5 5 AD 9 6 5 5 CD
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA Cpítulo SISTEMA DE COORDENADAS Demostrr que los puntos A ( 0,) B (,5) ; C ( 7,) D (, ) son los vértices de un cudrdo. Solución AB 9 6 5 5 BC 6 9 5 5 AD 9 6 5 5 CD
E-mail: grupociencia@hotmail.com 405 4466 Web-page: www.grupo-ciencia.jimdo.com 945 631 619
 1. En el prlelogrmo mostrdo en l figur M N son puntos medios. Hlle = ++ en función de 3 + D + C +3. En l figur muestr los vectores de inscritos en un cudro de 6m de ldo. Determine el vector unitrio del
1. En el prlelogrmo mostrdo en l figur M N son puntos medios. Hlle = ++ en función de 3 + D + C +3. En l figur muestr los vectores de inscritos en un cudro de 6m de ldo. Determine el vector unitrio del
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
UNIDAD: GEOMETRÍA POLÍGONOS CUADRILÁTEROS
 u r s o : Mtemátic Mteril N 13 GUÍ TÓRIO PRÁTI Nº 11 UNI: GOMTRÍ POLÍGONOS URILÁTROS POLÍGONOS FINIIÓN: Un polígono es un figur pln, cerrd, limitd por trzos llmdos ldos y que se intersectn sólo en sus
u r s o : Mtemátic Mteril N 13 GUÍ TÓRIO PRÁTI Nº 11 UNI: GOMTRÍ POLÍGONOS URILÁTROS POLÍGONOS FINIIÓN: Un polígono es un figur pln, cerrd, limitd por trzos llmdos ldos y que se intersectn sólo en sus
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Resolución de triángulos rectángulos
 Resoluión de triángulos retángulos Ejeriio nº 1.- Uno de los tetos de un triángulo retángulo mide 4,8 m y el ángulo opuesto este teto mide 4. Hll l medid del resto de los ldos y de los ángulos del triángulo.
Resoluión de triángulos retángulos Ejeriio nº 1.- Uno de los tetos de un triángulo retángulo mide 4,8 m y el ángulo opuesto este teto mide 4. Hll l medid del resto de los ldos y de los ángulos del triángulo.
ÁlgebrayGeometría. 5. Halla la ecuación de la circunferencia que pasa por (3, 0), ( 1, 0) y (0, 3).
 ÁlgebryGeometrí 1. ) Ddos tres puntos A, B y C en el plno demuestr que l circunferenci de diámetro AC ps por B siysólosielánguloâbc es recto. b) Ddos dos puntos A y B del plno y un rect r, determin, cundo
ÁlgebryGeometrí 1. ) Ddos tres puntos A, B y C en el plno demuestr que l circunferenci de diámetro AC ps por B siysólosielánguloâbc es recto. b) Ddos dos puntos A y B del plno y un rect r, determin, cundo
1. Perímetro y área de los polígonos (I) Halla mentalmente el perímetro y el área de un rectángulo que mide 60 m de largo y 40 m de alto.
 13 Perímetros y áres 1. Perímetro y áre de los polígonos (I) Hll mentlmente el perímetro y el áre de un rectángulo que mide 60 m de lrgo y 40 m de lto. Perímetro: (60 + 40) = 00 m Áre = 60 40 = 400 m P
13 Perímetros y áres 1. Perímetro y áre de los polígonos (I) Hll mentlmente el perímetro y el áre de un rectángulo que mide 60 m de lrgo y 40 m de lto. Perímetro: (60 + 40) = 00 m Áre = 60 40 = 400 m P
LA ELIPSE EJERCICIOS RESUELTOS. Colegio Sor Juana Inés de la Cruz Sección Preparatoria Matemáticas III Bloque VII Ing. Jonathan Quiroga Tinoco
 LA ELIPSE EJERCICIOS RESUELTOS Colegio Sor Jun Inés de l Cruz Sección Preprtori Mtemátics III Bloque VII Ing. Jonthn Quirog Tinoco 1. Pr encontrr l ecución de l elipse con centro en el origen, un foco
LA ELIPSE EJERCICIOS RESUELTOS Colegio Sor Jun Inés de l Cruz Sección Preprtori Mtemátics III Bloque VII Ing. Jonthn Quirog Tinoco 1. Pr encontrr l ecución de l elipse con centro en el origen, un foco
( ) 4. Colegio Diocesano Sagrado Corazón de Jesús. MATEMÁTICAS I / 1º Bachillerato C y T LOGARTIMOS. log. log. log. 1 log log 3.
 Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
60 α α. 3 lados 2 lados 3 lados. α 1. (0 < α n. Rectángulo:
 Personl Trinig for PSU nro.1. Prof. hef. Triángulos I: Propieddes ásics efinición dos los puntos,, ; se define triángulo como l reunión. P = punto interior Q = punto eterior ê 2 Q c P ê 1 φ b ê 3 Notción
Personl Trinig for PSU nro.1. Prof. hef. Triángulos I: Propieddes ásics efinición dos los puntos,, ; se define triángulo como l reunión. P = punto interior Q = punto eterior ê 2 Q c P ê 1 φ b ê 3 Notción
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA
 Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN:
 TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
FICHA DE TRABAJO. Bimestre IVº 4ºgrado - sección A B C D Ciclo IVº Fecha: - 11-10 Área : Matemática POLIEDROS REGULARES E IRREGULARES
 I TRJ Nombre Nº orden imestre IVº 4ºgrdo - sección iclo IVº ech: - 11-10 Áre : temátic Tem LIRS RULRS IRRULRS LIRS RULRS s quel poliedro en el cul sus crs son regiones poligonles congruentes entre sí,
I TRJ Nombre Nº orden imestre IVº 4ºgrdo - sección iclo IVº ech: - 11-10 Áre : temátic Tem LIRS RULRS IRRULRS LIRS RULRS s quel poliedro en el cul sus crs son regiones poligonles congruentes entre sí,
La Elipse. B( 0, b ) P( x, y ) a b. B'( 0, -b ) PF' PF VV ' (x + c) + y = 2a (x c) + y elevando al cuadrado (x + c) + y = 2a (x c) + y
 L Elipse Regresr Wikispces L elipse es el conjunto de todos los puntos P de un plno, tles que l sum de ls distncis de culquier punto dos puntos fijos del plno es constnte y su ecución se llm ecución ordinri.
L Elipse Regresr Wikispces L elipse es el conjunto de todos los puntos P de un plno, tles que l sum de ls distncis de culquier punto dos puntos fijos del plno es constnte y su ecución se llm ecución ordinri.
RELACIONES MÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 TUTORIAL DE PREPARAIÓN MATEMATIA 009 RELAIONES MÉTRIAS EN EL TRIÁNGULO RETÁNGULO I.- MARO TEORIO DEPTO. DE MATEMATIA Ls relciones métrics en un triángulo rectángulo son 5 relciones plicles sólo este tipo
TUTORIAL DE PREPARAIÓN MATEMATIA 009 RELAIONES MÉTRIAS EN EL TRIÁNGULO RETÁNGULO I.- MARO TEORIO DEPTO. DE MATEMATIA Ls relciones métrics en un triángulo rectángulo son 5 relciones plicles sólo este tipo
TRIGONOMETRÍA (4º OP. A)
 SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
Tema 6: LA DERIVADA. Índice: 1. Derivada de una función.
 LA DERIVADA Tem 6: LA DERIVADA Índice:. Derivd de un unción... Derivd de un unción en un punto... Interpretción geométric.3. Derivds lterles..4. Función derivd. Derivds sucesivs.. Derivbilidd y continuidd.
LA DERIVADA Tem 6: LA DERIVADA Índice:. Derivd de un unción... Derivd de un unción en un punto... Interpretción geométric.3. Derivds lterles..4. Función derivd. Derivds sucesivs.. Derivbilidd y continuidd.
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
Módulo 6. Trigonometría
 Seminrio Universitrio Mtemátic Módulo 6 Trigonometrí L mtemátic compr los más diversos fenómenos y descubre ls nlogís secrets que los unen Joseph Fourier ÁNGULO ORIENTADO Pr comenzr trbjr con trigonometrí
Seminrio Universitrio Mtemátic Módulo 6 Trigonometrí L mtemátic compr los más diversos fenómenos y descubre ls nlogís secrets que los unen Joseph Fourier ÁNGULO ORIENTADO Pr comenzr trbjr con trigonometrí
153 ESO. La mayoría de los hombres nacen como originales y terminan como copias. Oriental
 L myorí de los omres ncen como originles y terminn como copis 15 ESO Orientl ÍNDICE: MILLA NÁUTICA PISTA DE ATLETISMO 1. FÓRMULAS FUNDAMENTALES PARA CÁLCULO DE LONGITUDES, SUPERFICIES Y VOLÚMENES. LONGITUDES
L myorí de los omres ncen como originles y terminn como copis 15 ESO Orientl ÍNDICE: MILLA NÁUTICA PISTA DE ATLETISMO 1. FÓRMULAS FUNDAMENTALES PARA CÁLCULO DE LONGITUDES, SUPERFICIES Y VOLÚMENES. LONGITUDES
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
 Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Haga clic para cambiar el estilo de título
 Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
PÁGINA 76. sen 34 = BC AB = = 0,56. cos 34 = AC AB = = 0,82. tg 34 = BC AC = = 0,68. Pág mm. 35 mm. 51 mm
 Soluciones a las actividades de cada epígrafe PÁGIN 76 Pág. 1 1 Dibuja sobre un ángulo como el anterior, 34, un triánguo rectángulo mucho más grande. Halla sus razones trigonométricas y observa que obtienes,
Soluciones a las actividades de cada epígrafe PÁGIN 76 Pág. 1 1 Dibuja sobre un ángulo como el anterior, 34, un triánguo rectángulo mucho más grande. Halla sus razones trigonométricas y observa que obtienes,
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
PSU Matemática NM-4 Guía 22: Congruencia de Triángulos
 Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES
 71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
UNIDAD: GEOMETRÍA TRIÁNGULO RECTÁNGULO
 u r s o : Mtemátic 3º Medio Mteril Nº MT-16 UNI: GOMTÍ TIÁNGULO TÁNGULO TOM ITÁGOS n todo triángulo rectángulo, l sum de ls áres de los cudrdos construidos sobre sus ctetos, es igul l áre del cudrdo construido
u r s o : Mtemátic 3º Medio Mteril Nº MT-16 UNI: GOMTÍ TIÁNGULO TÁNGULO TOM ITÁGOS n todo triángulo rectángulo, l sum de ls áres de los cudrdos construidos sobre sus ctetos, es igul l áre del cudrdo construido
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
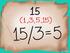 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
SELECTIVIDAD CASTILLA Y LEÓN/ MATEMÁTICAS / ANÁLISIS DE FUNCIONES
 Junio 009 SELECTIVIDAD CASTILLA Y LEÓN/ MATEMÁTICAS / ANÁLISIS DE FUNCIONES PR-.- Un cmpo de tletismo de 00 metros de perímetro consiste en un rectángulo y dos semicírculos en dos ldos opuestos, según
Junio 009 SELECTIVIDAD CASTILLA Y LEÓN/ MATEMÁTICAS / ANÁLISIS DE FUNCIONES PR-.- Un cmpo de tletismo de 00 metros de perímetro consiste en un rectángulo y dos semicírculos en dos ldos opuestos, según
Ejercicios de optimización
 Ejercicios de optimizción 1. Entre todos los triángulos isósceles de perímetro 0, cuál es el de áre máxim? Función mximizr: A yh Relcionr vribles: Estudimos l función: h h y x h x y x y 0 x 0y 0 y 0 0y
Ejercicios de optimizción 1. Entre todos los triángulos isósceles de perímetro 0, cuál es el de áre máxim? Función mximizr: A yh Relcionr vribles: Estudimos l función: h h y x h x y x y 0 x 0y 0 y 0 0y
Resolución del examen de Matemáticas II de Selectividad Andalucía Junio de 2006
 Resolución del emen de Mtemátics II de Selectividd Andlucí Junio de 6 Antonio Frncisco Roldán López de Hierro * de junio de 6 Opción A Ejercicio [ 5 puntos] Determin un punto de l curv de ecución y e pendiente
Resolución del emen de Mtemátics II de Selectividd Andlucí Junio de 6 Antonio Frncisco Roldán López de Hierro * de junio de 6 Opción A Ejercicio [ 5 puntos] Determin un punto de l curv de ecución y e pendiente
12 Áreas. y volúmenes. 1. Área de figuras planas
 Áres y volúmenes. Áre de figurs plns Hll mentlmente ls áres de un cudrdo de 7 m de ldo y de un rectángulo de 9 m de lrgo y 5 m de lto. Áre del cudrdo: 49 m Áre del rectángulo: 45 m P I E N S A Y C C U
Áres y volúmenes. Áre de figurs plns Hll mentlmente ls áres de un cudrdo de 7 m de ldo y de un rectángulo de 9 m de lrgo y 5 m de lto. Áre del cudrdo: 49 m Áre del rectángulo: 45 m P I E N S A Y C C U
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA
 SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 007 - Noiones de Trigonometrí: L trigonometrí se dedi l estudio de ls reliones que existen entre ls medids de los ángulos y ldos de un triángulo.
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 007 - Noiones de Trigonometrí: L trigonometrí se dedi l estudio de ls reliones que existen entre ls medids de los ángulos y ldos de un triángulo.
RESOLUCIÓN DE TRIÁNGULOS
 RESOLUIÓN DE TRIÁNGULOS Págin 0 PR EMPEZR, REFLEXION Y RESUELVE Prolem Pr lulr l ltur de un árol, podemos seguir el proedimiento que utilizó Tles de Mileto pr llr l ltur de un pirámide de Egipto: omprr
RESOLUIÓN DE TRIÁNGULOS Págin 0 PR EMPEZR, REFLEXION Y RESUELVE Prolem Pr lulr l ltur de un árol, podemos seguir el proedimiento que utilizó Tles de Mileto pr llr l ltur de un pirámide de Egipto: omprr
La hipérbola es el lugar geométrico de todos los puntos cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante e igual a 2a.
 INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
PROPORCIONALIDAD DIRECTA E INVERSA
 PROPORCIONALIDAD DIRECTA E INVERSA Rzón entre dos números Siempre que hblemos de Rzón entre dos números nos estremos refiriendo l cociente (el resultdo de dividirlos) entre ellos. Entonces: Rzón entre
PROPORCIONALIDAD DIRECTA E INVERSA Rzón entre dos números Siempre que hblemos de Rzón entre dos números nos estremos refiriendo l cociente (el resultdo de dividirlos) entre ellos. Entonces: Rzón entre
XI. LA HIPÉRBOLA LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO
 XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
DIVERSIFICACIÓN CURRICULAR
 ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
pág CONTINUIDAD 1.1 FUNCIÓN CONTINUA EN UN PUNTO Decimos que f es continua en a si:
 .- CONTINUIDAD TEMA 6 Continuidd, Cálculo Diferencil. FUNCIÓN CONTINUA EN UN PUNTO Decimos que f es continu en si: Lim f( ) f( ) Pr que un función se continu en un punto se h de cumplir: º f ( ) D º Lim
.- CONTINUIDAD TEMA 6 Continuidd, Cálculo Diferencil. FUNCIÓN CONTINUA EN UN PUNTO Decimos que f es continu en si: Lim f( ) f( ) Pr que un función se continu en un punto se h de cumplir: º f ( ) D º Lim
Colegio Diocesano Sagrado Corazón de Jesús EJERCICIOS MATEMÁTICAS 3º ESO VERANO 2015
 Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
PROBLEMAS DE ESTÁTICA
 UCM PEMS DE ESÁIC undmentos ísicos de l Ingenierí. Deprtmento ísic plicd UCM Equipo docente: ntonio J rbero lfonso Cler Mrino Hernández. ES grónomos lbcete Pblo Muñiz Grcí José. de oro Sáncez EU. I.. grícol
UCM PEMS DE ESÁIC undmentos ísicos de l Ingenierí. Deprtmento ísic plicd UCM Equipo docente: ntonio J rbero lfonso Cler Mrino Hernández. ES grónomos lbcete Pblo Muñiz Grcí José. de oro Sáncez EU. I.. grícol
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
TEMA 1: FUNCIONES. LÍMITES Y CONTINUIDAD
 Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
1. Perímetro y área de los polígonos (I) Halla mentalmente el perímetro y el área de un rectángulo que mide 60 m de largo y 40 m de alto.
 13 Perímetros y áres 1. Perímetro y áre de los polígonos (I) Hll mentlmente el perímetro y el áre de un rectángulo que mide 60 m de lrgo y 40 m de lto. Perímetro: (60 + 40) = 00 m Áre = 60 40 = 400 m P
13 Perímetros y áres 1. Perímetro y áre de los polígonos (I) Hll mentlmente el perímetro y el áre de un rectángulo que mide 60 m de lrgo y 40 m de lto. Perímetro: (60 + 40) = 00 m Áre = 60 40 = 400 m P
