Fijación de primas de seguros bajo técnicas de robustez bayesiana
|
|
|
- Antonia Casado López
- hace 8 años
- Vistas:
Transcripción
1 Fijación de primas de seguros bajo écnicas de robusez bayesiana Gómez Déniz E. Deparameno de Méodos Cuaniaivos en Economía y Gesión. Universidad de Las Palmas de G.C. Fac. CC. Económicas. Módulo D. Campus de Tafira. 357 Las Palmas de G.C. Tfno: Fax: emilio@empresariales.ulpgc.es Pérez Sánchez J. M. Deparameno de Méodos Cuaniaivos en Economía y Gesión. Universidad de Las Palmas de G.C. Fac. CC. Económicas. Módulo D. Campus de Tafira. 357 Las Palmas de G.C. Tfno: Fax: josema@empresariales.ulpgc.es Clasificación AMS: 6F5 6P5. Invesigación parcialmene financiada por la Dirección General de Invesigación Cienífica y Técnica (España) mediane proyeco PB Los auores de la Universidad de Las Palmas de G.C. desean asimismo agradecer la financiación parcial de la Dirección General de Universidades e Invesigación del Gobierno Auónomo de Canaria proyeco 75. Los auores agradecen los valiosos comenarios de un evaluador anónimo cuyas aporaciones han mejorado sensiblemene ese rabajo. Los auores agradecen muy sinceramene los comenarios del evaluador que han ayudado a mejorar el rabajo.
2 Fijación de primas de seguros bajo écnicas de robusez bayesiana Gómez Déniz E. Pérez Sánchez J. M. ESUMEN La esadísica acuarial ha abordado el problema de la arificación en los seguros de no vida desde un puno de visa clásico y bayesiano clásico. En los primeros el parámero de riesgo se considera conocido mienras que en los segundos se considera aleaorio. En ese rabajo se esudia la prima obenida siguiendo ambas meodologías en el modelo colecivo de la eoría del riesgo. La uilización de la meodología bayesiana supone una confianza absolua en la disribución a priori del parámero de riesgo y eso ha sido ampliamene criicado por los esadísicos no bayesianos. Para salvar esa siuación y uilizando la meodología de robusez bayesiana mediremos la sensibilidad de la prima obenida en un conexo bayesiano con respeco a perurbaciones en la disribución a priori del parámero de riesgo uilizando la clase de ε -conaminación. Palabras Clave: Teoría de la Credibilidad Principio de Cálculo de Prima obusez Bayesiana Clase de ε -conaminación. ABSTACT Acuarial saisics have approached arifficaion problem in no-life insurances from a Bayesian and classic poin of view. From he classic poin of view parameer is known while he bayesians considered i random. In his work we sudied risk premium under boh mehodologies in he collecive model of he isk Theory. Bayesian mehodology supposes an absolue confidence in he prior disribuion of he risk parameer and i has been widely criicized by he classic saisicians. To save his siuaion and using he Bayesian sensiiviy mehodology we will measure he sensiiviy of Bayesian Premium wih respec o disurbances in he prior disribuion from he risk parameer using ε -conaminaed class. Key words: Credibiliy Theory Premium Calculaion Principle Bayesian obusness ε - Conaminaion Class.
3 . INTODUCCIÓN Los acuarios son las personas que raan con oda clase de problemas maemáicos y esadísicos en seguros. Las compañías de seguros acepan riesgos de sus clienes los asegurados frene a un ciero precio denominado prima. La eoría de la credibilidad se basa en agrupar las pólizas referenes a un mismo riesgo con una serie de caracerísicas comunes en un colecivo al cual le corresponde como al una deerminada prima coleciva. Pero cada póliza a su vez iene un conjuno de caracerísicas específicas que la diferencia de las demás pólizas. Esas caracerísicas en la mayoría de los casos son inobservables o difíciles de cuanificar pero obviamene han de enerse en cuena para calcular las primas de riesgo individuales. La eoría de la credibilidad esima dichas primas basándose en la información pasada de la experiencia de siniesralidad y las fórmulas obenidas son en muchas ocasiones una suma ponderada de la prima coleciva del riesgo y la media empírica de las indemnizaciones pagadas. El facor de ponderación uilizado se conoce con el nombre de facor de credibilidad. Hasa hace poco se inenaba deerminar la prima para el colecivo sin preocuparse excesivamene por la heerogeneidad de la carera. Sin embargo la endencia acual y fuura parece considerar ambién las caracerísicas pariculares de cada riesgo. Los méodos bayesianos juegan aquí un papel muy imporane pues permien incorporar la información resulane de la hisoria paricular de cada riesgo. En la prácica el cálculo de la prima requiere que la disribución del riesgo X bajo consideración sea conocida (o al menos cieros momenos cuaniles ec.). Nosoros consideraremos como es usual en eoría de la credibilidad el caso en el que la disribución de X esá especificada salvo un parámero desconocido. La erminología que uilizaremos será la siguiene. Supondremos variables aleaorias X X X... ales que oma valores en algún espacio paramérico (generalmene un subconjuno de la reca real) y dado X X X... son independienes e idénicamene disribuidas con función de densidad de probabilidad f ( x ). La prima nea de riesgo que la compañía aseguradora cobra al riesgo X viene dada por P ( ) E [ X ] bajo el supueso de que el parámero sea conocido. Uno de los principales ópicos en eoría de la credibilidad es precisamene la inceridumbre de dicho parámero (Eichenauer J. e al. (988); Gómez E. e al. (999); Klugman S. e al. (998); enre oros). Asumiremos pues una disribución a priori ( ) 3
4 (función esrucura en érminos acuariales) para dicho parámero. Ahora suponiendo para el riesgo alguna experiencia de siniesralidad m la prima Bayesiana vendrá dada por ( m ) E { E [ ]} P X. Muchos rabajos se han publicado en eoría de la credibilidad acerca de la aproximación Bayesiana (Herzog T. (994) ; Gómez E. e al. (999); Klugman S. e al. (998); enre oros). Sin embargo muy pocos han raado el asuno de la robusez bayesiana. Eichenauer J. e al. (988); Gómez E. e al. (998); Gómez E. e al. (999) Heilmann W. y Schröer K. (987) son algunos ejemplos de ellos. El problema de inerés en ese arículo será el análisis bayesiano basado en información a priori parcial en eoría de la credibilidad. El análisis de robusez bayesiano ha recibido una aención considerable en las úlimas dos décadas y numerosos auores han propueso soluciones para ese problema (Berger J. (994); Moreno E. y Cano J. (99); Sivaganesan S. y Berger J. (989); Sivaganesan S. (99); enre oros). Bajo dicho análisis el acuario será incapaz de especificar una única disribución a priori para el parámero de riesgo. Aunque exisen numerosos ipos de clases de disribuciones a priori que pueden uilizarse dedicaremos nuesra aención a la clase de ε -conaminación Γ ε { ( ) ( ε ) ( ) + ε q ( ): q Q} donde ε mide la inceridumbre que se iene en la disribución a priori inicial y Q es una clase plausible de conaminaciones. Esa clase ha sido uilizada en siuaciones diversas (Berger J. (994); Moreno E. y Cano J. (99); Sivaganesan S. y Berger J. (989); enre oros) para esudiar la sensibilidad de alguna canidad a poseriori de inerés medida generalmene por el rango de variación de la misma. El arículo esá organizado como sigue. En la sección se realiza una inroducción a la eoría de la credibilidad y se procede al cálculo de la prima nea en sus disinas versiones. En la sección 3 exponemos el modelo gamma-gamma de la eoría del riesgo. En la sección 4 procedemos a flexibilizar las enradas que exige un análisis bayesiano inercambiando la disribución a priori inicial por oda una clase de disribuciones posibles. En la sección 5 se ilusran odas las ideas aneriores con ejemplos numéricos. En la sección 6 presenamos las propiedades exigibles a un principio de cálculo de prima y proponemos un nuevo sisema de arificación basado en la robusez bayesiana. Finalmene la sección 7 concluye con algunos comenarios y posibles líneas abieras para fuuras invesigaciones. 4
5 . LA TEOIA DE LA CEDIBILIDAD Y EL PINCIPIO DE PIMA NETA El problema de la credibilidad se basa en esimar las ponderaciones que afecan a la experiencia de siniesralidad de una póliza respeco a la experiencia de un colecivo al que perenece el suscripor de dicha póliza. La cuesión básica es deerminar hasa qué puno es creíble la experiencia observada de un asegurado individual en relación a la experiencia de un colecivo al que el asegurado perenece. En lo que sigue asumiremos que la siniesralidad de un riesgo o asegurado es una variable aleaoria X con función de densidad de probabilidad f ( x ) y que el valor de es fijo para un riesgo dado aunque desconocido. Si deseamos disinguir en qué año o período ocurre la siniesralidad X escribimos X i para la siniesralidad en el año o período i.... Luego supondremos variables aleaorias X X X... ales que X i son independienes dado e idénicamene disribuidas. Denoaremos como es usual en eoría de la credibilidad mediane ( ) la función de densidad de a la que se le llama función esrucura. En érminos bayesianos esa función de densidad represena una opinión a priori subjeiva acerca del parámero desconocido que puede represenar por ejemplo la propensión de un conducor a reclamar un siniesro y ( ) puede describir de qué modo esa propensión se disribuye a ravés de la población de conducores asegurados. Luego ( ) represena nuesra opinión a priori acerca de un conducor seleccionado aleaoriamene de la carera. f (x) describe la disribución de la variable experiencia de siniesralidad para un conrao elegido aleaoriamene de la carera y es ( x) f ( x ) ( ) d f () que se raa de la densidad de X incondicional de. En eoría de la credibilidad se usan los érminos individual y colecivo como sinónimos de conrao y carera y se disingue enre prima de riesgo prima coleciva y prima bayesiana. La prima nea de riesgo viene dada por ( ) f ( x ) dx P x () 5
6 y la prima nea de riesgo coleciva se obiene como ( x) dx x f ( x ) ( ) d P ( ) ( ) P d. (3) x f Si ahora en un período de iempo se observan las indemnizaciones x x... x y asumiendo independencia de un período a oro la disribución a poseriori viene dada uilizando el eorema de Bayes por ( ) ( m ) ( ) ( m ) ( ) d f m (4) f donde f m ) f ( x x... x ) es la verosimiliud observada. Esa función esrucura a poseriori ( (disribución a poseriori) nos permie obener la prima nea bayesiana que se calcula de la misma forma que la prima coleciva inercambiando en (3) la disribución a priori ( ) por la disribución a poseriori ( ). Ahora la prima nea bayesiana resula m ( m ) P( ) ( m ) d. P La prima de riesgo represena la asa eórica que la compañía de seguros cobraría a un individuo dado al asegurarse. Para su cálculo la compañía (el acuario) debe conocer la forma de la disribución de probabilidad del riesgo y los parámeros de esa disribución. Si se dispone de esa información la prima de riesgo se podrá calcular y por lo ano no exisirán moivos para hacer ajuses de credibilidad. Sin embargo en eoría de la credibilidad se supone que esa información no esá disponible. En ese caso la prima que la compañía cobra es la coleciva. Para su cálculo se requiere que el acuario especifique una disribución a priori para el parámero de riesgo. La información que para ello se necesia se puede obener de los daos de una población de conraos similares. La prima bayesiana como ya dijimos anes es muy similar a la prima coleciva. Considera para su cálculo la información a priori acerca de los parámeros del proceso de reclamaciones y la información muesral o experiencia de siniesralidad. Uilizando ambas informaciones se calcula la disribución a poseriori para siguiendo el mismo camino que en el cálculo de la prima coleciva obener la prima bayesiana. Evidenemene la meodología seguida para el cálculo de la prima es solamene una posibilidad de acuar enre la amplia gama de principios de cálculo enre los que elegir. Algunos principios de 6
7 cálculo de primas más comunes son el de prima nea exponencial Esscher y varianza enre oros. Una excelene revisión y discusión de ese ópico se encuenra en Heilmann W. (989). Los acuarios gusan de uilizar primas de la forma [ ( m )] ( ) ZP g + Z (5) P con [ ] Z y lim Z donde g es un esimador máximo verosímil de. Aquí [ g( m )] P podría denominarse prima de riesgo individual y P prima coleciva. La expresión (5) recibe el nombre de fórmula de credibilidad y Z es el facor de credibilidad. Bühlmann H. (967) fue el primero en dar una formulación explícia para Z basada en la aproximación por mínimos cuadrados obeniendo Z donde + k k [ V ( X )] [ E( X )] E. (6) V V (.) represena la varianza y Z y Z se inerprean como la credibilidad parcial de los daos observados y de la información a priori. 3. EL MODELO. CALCULO DE PIMAS Un modelo usado con frecuencia en los sisemas de arificación en seguros asume que el riesgo iene la disribución gamma Γ ( ϑ) para la canidad de indemnización (Bühlmann 97) con una disribución ambién gamma a lo largo de la población para el parámero desconocido. Bajo dicho modelo f(x) viene dada por f ϑ x ( x ) f ( x ) ( ) d x e Γ Γ ϑ a ( ϑ ) ( b ) b b e a d ϑ b ϑ ( b + ϑ ) x a ϑ + ( + ) Γ Γ ( ) Γ ( ) b a x x a e d b Γ ( ϑ ) Γ ( b ) ( a + x ) b ϑ + ϑ b que resula ser una disribución generalizada de Pareo GPar(abϑ ). 7
8 La prima nea de riesgo se obiene uilizando () y es ϑ P ( ). La prima de riesgo coleciva o a priori es de (3) P aϑ > b b ya que se raa de la esperanza de una disribución generalizada de Pareo GPar(abϑ ). Ahora si en un período de iempo se observan las indemnizaciones x x... x la probabilidad de ese suceso (la verosimiliud) es ϑ ϑ m f ( m ) ( x x x ) ( ) e m xi Γ ϑ i mienras que la disribución a poseriori de dada la muesra es de (4) b + ϑ ( a + m ) ( m ) e que resula ser una disribución ambién gamma con parámeros a + m y b + ϑ. La prima bayesiana se calcula de la misma manera que la prima coleciva susiuyendo ( ) por ( ) resulando m ( a + m ) ϑ P ( m ). (7) b + ϑ En nuesro caso donde X Γ( ϑ) y Γ( a b) se iene E [ X ] ϑ / V [ X ] ϑ / EV [ ( X )] E ( ϑ / ) ϑa ( b )( b ) [ ( X )] V ( / ) VE ϑ a ( b ) ( b ). 8
9 Luego usando las expresiones de (6) Z. + ( b ) / ϑ Obsérvese que (7) puede reescribirse como P ( m ) ( a b + + m ) ϑ ϑ b ϑ m + ϑ + b b + ϑ aϑ b Z m + ( Z ) P. Teniendo en cuena que si ~ ( ϑ) X Γ con ϑ conocido enonces el esimador de máxima verosimiliud de para una muesra de amaño es ϑ ( xi ) en cuena que ( ) ϑ P que P ( g ( m )) P ( ) ϑ m. y de aquí se deduce eniendo La prima bayesiana pues en nuesro modelo adopa la forma de una fórmula de credibilidad con facor de credibilidad como en (6). 4. CONSIDEACIONES MAS FLEXIBLES PAA EL CALCULO DE LA PIMA BAYESIANA A pesar de los avances en el campo de la esadísica bayesiana varios son los problemas que suelen achacarse a esa aproximación. La elección de la disribución a priori que iene un carácer subjeivo al esar basada en la información previa acumulada por el invesigador. Sin embargo en la prácica puede ser muy difícil discernir enre cieras disribuciones con caracerísicas similares. Por ejemplo podemos esar convencidos de que la disribución a priori es unimodal y simérica pero disinguir enre las disribuciones normal y Cauchy puede resular muy difícil. En oras ocasiones la especificación de la disribución a priori se hace difícil porque la decisión ha de ser omada por un grupo de personas que pudieran ener opiniones a priori diferenes. Para salvar esa dificulad y desde hace algún iempo se rabaja en análisis bayesiano con una meodología que consise en procesar información a priori más flexible que la que se exige en un análisis bayesiano clásico. Bajo esas ideas el problema a raar consise en realizar un análisis de sensibilidad bayesiano en el proceso de arificación de primas de seguros. Por ejemplo si las creencias a priori del acuario ienen una forma menos elaborada que una disribución a priori nos planeamos si se podrían ampliar las enradas del análisis bayesiano permiiendo que la 9
10 especificación a priori fuera una clase o familia de disribuciones en lugar de una sola. Para concrear esa clase podríamos incorporar caracerísicas que pudieran ser muy claras para un acuario como la unimodalidad conocimieno de algunos cuaniles ec. Sobre esa familia el acuario calcularía los exremos inferior y superior de la prima a cobrar de modo que si la diferencia enre esos dos valores denominada rango de variación es grande se habla de carencia de robusez; por el conrario si la diferencia es pequeña se dice enonces que el modelo es robuso. La carencia de robusez debe inerprearse de la siguiene forma: densidades muy parecidas no producen canidades próximas y de ahí que el acuario deberá omar sus decisiones con mucha precaución. Por conra un modelo robuso debe inerprearse de esa ora forma: las decisiones del acuario no se ver susancialmene modificadas con un elemeno u oro de la clase. Una familia que permie realizar un análisis de sensibilidad como el aneriormene señalado es la clase de conaminación (Berger J. (994); Moreno E. y Cano J. (99); Sivaganesan S. y Berger J. (989); enre oros). En ella la disribución a priori del parámero esá denro de una clase de disribuciones a priori de la forma Γε { ( ε) + ε q : q Q} (8) en la que [ ] ε deermina la canidad de inceridumbre en la disribución a priori inicial y Q es una clase de posibles conaminaciones. Un inerés naural del análisis de robusez consise en enconrar el rango de variación de una magniud a poseriori de inerés en nuesro caso la prima nea bayesiana; luego esamos { } ineresados en calcular el inf P ( m ); y el sup P ( m ) Γ ε para ello se expone a coninuación. Para la clase de conaminación en (8) se iene que { ; } Γ ε. La meodología a seguir ( m ) f f ( m ) ( ) ( m ) ( ) d ( ε ) ( m ) f ( m ) ( ) ( ) ( ) ( ) d + ε q m f m q ( ε ) f ( m ) ( ) d + ε f ( m ) q( ) d d la prima bayesiana para el modelo de la sección 3 puede escribirse como
11 ϑ P ( m ) ( m ) d ( ε ) P ( m ) ( ) ( ) ( ) ( ) ( ) ( ) f m d + εp q m f m q d ( ε ) f ( m ) ( ) d + ε f ( m ) q( ) d. (9) En ese arículo desarrollaremos el análisis de sensibilidad de la prima bayesiana para las clases i ε Γ { ( ε ) + ε q : q Q } i i omando como clases conaminanes Q {Todas las disribuciones de probabilidad} y Q {Disribuciones unimodales con la misma moda que ( ) }. Los siguienes resulados muesran cómo calcular el rango de variación de la prima bayesiana que pasa por calcular los exremos de una función de una variable. Lema. Si X Γ( ϑ) y Γ( a b) enonces: inf P ( m ) inf Γε 3 P ( m ) + ( ) + ( ) ε f ( ) ( ) d ( ) ε ( ϑ / ) f ( m ) ) ( ) donde ( ) m como en (7). El supremo se obiene reemplazando inf por sup. y P ( m ) 3 ( Demosración.- Basa aplicar el lema A.. de Sivaganesan S. y Berger J. (989) a la expresión (9).
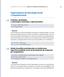
12 Γ Lema. Si X Γ( ϑ) y Γ( a b) enonces inf P ( m ) infz ( z) donde ε P ( z) ( m ) + + ( / z) ( / z) + z + z 3 ( ) d ( ) d si z > y () P ( m ) + ( ) + ( ) 3 con ( ) 3 ( ) y ( m ) P como en el lema. El supremo se obiene reemplazando inf por sup. Demosración.- Basa aplicar el lema 3.. y el lema A.. de Sivaganesan S. y Berger J. (989) a la expresión (9). Como medida de la robusez uilizaremos el facor de sensibilidad relaiva inroducido por Sivaganesan (99) y que adapado a nuesro problema viene dado por S i sup i { P ( m ); Γε } inf P ( m ) P ( m ) i { ; Γ } ε % ( i ) que puede inerprearse como el porcenaje de variación de la prima calculada para la disribución alrededor de la prima calculada para la disribución a priori inicial. En la sección 5 se aplican los resulados de esa sección a casos concreos. 5. APLICACIÓN Para ilusrar las ideas expuesas aneriormene desarrollaremos res ejemplos numéricos. Supongamos que el acuario confía que la variable indemnización de reclamaciones iene una disribución gamma con media en orno a 5 unidades monearias (u.m.) y que la indemnización
13 media más frecuene la moda esá en orno a.5 u.m. Un modelo que refleje lo anerior puede ser el siguiene X Γ( ) Γ(6) donde por comodidad compuacional rabajaremos con los daos divididos por. Tomaremos como observación muesral m la canidad media de indemnización observada en los úlimos años de vigencia de la póliza que supondremos es de y 5 u.m. para res ejemplos considerados. Después de los cálculos oporunos se obienen los rangos de variación y los valores del facor S que aparecen en las figuras y 3. Se ha omado como grado de conaminación valores desde hasa el.35 con pasos de.5 observándose que el facor S no resula paricularmene alo en ninguno de los casos aquí considerados; luego los resulados son razonablemene robusos. Por ejemplo para el caso en que la media muesral es de 5 u.m. se obiene como valor de la prima bayesiana 5.7 u.m. omando el facor S valores desde.3 hasa el 7.69% para conaminaciones con Q. Ese facor se reduce hasa omar los valores desde.47 hasa el 3.6% para conaminaciones con Q. Luego desde nuesro puno de visa la compañía aseguradora puede senirse ranquila cobrando en ese caso como valor de la prima cualquiera de los que se encuenren en el inervalo de variación. Por ejemplo si el acuario confía en una disribución a priori gamma en un 95% ( ε. 5 ) en el caso de conaminaciones unimodales la prima bayesiana oma valores en el inervalo [ ]. La prima coleciva ambién en ese ejemplo oma el valor 6.66 u.m. de lo que resula Z.574. Eso quiere decir que la información muesral o daos observados pondera un 57% mienras la información del colecivo o información a priori lo hace un 43%. En érminos acuariales se comena que la información muesral es creíble al 57% y la del colecivo al 43%. Para un asegurado que se incorpore a la compañía de seguros y del que no dispongamos de hisorial anerior la compañía aseguradora le cobraría la prima coleciva con una credibilidad del 43%; en la medida que se vaya disponiendo de experiencia de reclamaciones para ese sujeo la prima que se le cobraría se le iría ajusando adecuadamene. Para finalizar con ese aparado digamos que odos los cálculos han sido elaborados con el sofware Mahemaica y los gráficos con el sofware Malab en un Penium II a 55 Mh. y un iempo de cómpuo relaivamene rápido. 3
14 Figura. angos de variación de la prima bayesiana con media Inferior y superior de la prima bayesiana Grado de conaminación Todas las disribuciones Disribuciones unimodales Facor S Grado de conaminación Todas las disribuciones Disribuciones unimodales Figura. angos de variación de la prima bayesiana con media Inferior y superior de la prima bayesiana Grado de conaminación Todas las disribuciones Disribuciones unimodales Facor S Grado de conaminación Todas las disribuciones Disribuciones unimodales 4
15 Figura 3. angos de variación de la prima bayesiana con media 5 Inferior y superior de la prima bayesiana Grado de conaminación Facor S Grado de conaminación Todas las disribuciones Disribuciones unimodales Todas las disribuciones Disribuciones unimodales 6. TAIFICACIÓN ALTENATIVA DEL IESGO En la lieraura acual no exise un sisema axiomáico comúnmene acepado de propiedades que un principio de cálculo de prima debería saisfacer. Sin ser exhausivos conribuciones imporanes en esa maeria pueden enconrarse en Gerber H. (979) Heilmann W. (989) Hürlimann W. (994) Kuen S. y Yang H. (999) y Young V. (999) enre oros. Generalmene se acepa que las propiedades que un principio de cálculo de prima [ X ] P H debería saisfacer son: i. Sobreprima de seguridad no negaiva: P E [ X ]. Eso significa que para eviar la ii. ruina écnica la ganancia esperada será no negaiva. No esafa: La prima no excederá a la reclamación máxima posible r X eso es P r X. iii. Consisencia: Para cada riesgo X y cada consane c H [ X + c] H [ X ] + c. Eso significa que si el beneficio se incremena en una consane ésa iene que ser añadida a la prima. 5
16 iv. Adiividad: Si X y X son riesgos independienes siempre se endrá que cumplir [ X X ] H [ X ] H [ ] H + +. Eso quiere decir que la incorporación de riesgos X independienes no afecan a la prima oal. v. H [] c c para oda consane c X c con Prob[Xc] la prima a cobrar será c. vi. Homogeneidad posiiva: [ cx ] ch [ X ] conveniene para corregir efecos inflacionarios.. Eso significa que para un riesgo no aleaorio H para odo c que resula vii. H [ p X + qy ] ph [ X ] + qh [ Y ] p > q > ales que p + q. Es fácil probar que la prima nea de riesgo coleciva y bayesiana verifica odas las propiedades aneriores. La cuesión es averiguar si cualquier valor de la prima bayesiana conenida en el inervalo de variación [ inf P ( m ) i i { ; Γ } sup{ P ( m ); Γ } ] propiedades. Para esudiar eso obsérvese que de (9) se iene que ε ε sigue conservando esas P ( m ) P ( m ) + ε P ( ) f ( m ) q( ) + ε f ( m ) q( ) d d que puede reescribirse de la forma P ( m ) ε P P ( m ) + + ε f ( m ) q( ) d + ε f P ( m ) + + ε f ( m ) q( ) d + ε ( m ) + ( ) P ( m ) γp γ q ( m ) q( ) d f ( m ) q( ) ( ) f ( m ) q( ) ε f ( m ) q( ) d d d P ( ) f ( m ) q( ) f ( m ) q( ) d d con γ + ε f m ( ) q( ) d [ ] ya que ( ) q( ) d > f m. Luego la prima bayesiana obenida en el modelo de conaminaciones puede escribirse como una combinación convexa de dos primas bayesianas la calculada para la disribución a priori inicial y la 6
17 calculada para la disribución conaminane (esa es una prima eórica no calculable). A parir de aquí es fácil comprobar que las propiedades se conservan al pasar al modelo de conaminaciones con Q. Ahora pueso que Q Q se desprende que las propiedades son ambién válidas en el modelo de conaminaciones unimodales. La propuesa que hacemos nosoros es la siguiene. Si el modelo es robuso dado un ε y por ano para una confianza en la disribución a priori de ( ε ) % - la compañía aseguradora puede cobrar como valor de la prima cualquiera del inervalo de variación de la prima bayesiana. Esa políica de arificación novedosa en los escenarios acuariales le puede reporar a la compañía un elenco de valores a cobrar que pudiera solucionarle problemas de compeiividad acaparando mayor cuoa de mercado. 7. CONCLUSIONES Y POSIBLES EXTENSIONES En ese arículo se ha ilusrado el uso del análisis bayesiano robuso en eoría de la credibilidad para medir la sensibilidad de la prima nea bayesiana en el modelo gamma-gamma. El análisis bayesiano robuso asume inceridumbre en la función esrucura e inercambia ésa por clases de disribuciones a priori plausibles lo que proporciona un inervalo de variación de la prima bayesiana. Los resulados obenidos indican que se obiene una reducción significaiva del facor S cuando se considera la unimodalidad. Esa aproximación permie ofrecer resulados más flexibles que con los méodos Bayesianos clásicos lo que puede ser aprovechado por las compañías aseguradoras para resolverles problemas de compeiividad acaparando mayor cuoa de mercado. Una pequeña modificación en el lema podría llevarse a cabo si el acuario considera conveniene añadir la propiedad de simería a la de unimodalidad. Eso es posible reemplazando ( ) + z / z ( ) d ( ) + por / ( z) z z ( ) d (Sivaganesan S. y Berger J. (989)). Ora posible modificación sería considerar mixuras de disribuciones si el acuario desea considerar disribuciones bimodales (o mulimodales) como función esrucura que es razonable en muchos ramos de seguros. Lo fundamenal es que la clase de ε -conaminación es muy flexible y se puede rabajar con ella sin complicar demasiado los procedimienos maemáicos. Por oro lado la mayoría de los modelos bayesianos en credibilidad uilizan una aproximación bayesiana pura uilizando dos niveles el primero inroduce la verosimiliud y el segundo una disribución a priori para algún parámero de aquélla. Esa disribución coniene nuesro 7
18 conocimieno sobre las relaciones enre las disinas clases de asegurados. No es nuesra opinión a priori sobre una clase en paricular. Una solución a eso lo da el análisis bayesiano jerárquico incluyendo un ercer nivel. En el primer nivel como aneriormene se inroduce una disribución que describe las variaciones denro de cada grupo de asegurados; el segundo nivel incorpora una disribución que describe las variaciones enre los grupos; finalmene el ercer nivel proporciona una disribución a priori para los parámeros desconocidos en los niveles aneriores. Desaforunadamene en ese caso las écnicas bayesianas son complicadas desde el puno de visa analíico y sólo se ha desarrollado el modelo con disribuciones normales para los dos primero niveles e impropia para el ercero. Sin embargo es obvio que la disribución normal no resula adecuada para modelar escenarios acuariales por lo que resularía ineresane la invesigación de oros modelos en el análisis bayesiano jerárquico. Bibliografía Berger J. (994). "An Overview of obus Bayesian Analysis." TEST 3 pp Bühlmann H.(967). "Experience raing and credibiliy." Asin Bullein 5 II pp Bühlmann H.(97). Mahemaical Mehods in isk Theory. Springer. New York. Eichenauer J. Lehn J. y eig S. (988). "A gamma-minimax resul in credibiliy heory."insurance: Mahemaics and Economics 7 pp Gerber H. (979). An inroducion o mahemaical risk heory. Huebner Foundaion. Gómez E. Hernández A y Vázquez F. (998). Un análisis de sensibilidad del proceso de arificación en los seguros generales. Esudios de Economía Aplicada 9 pp Gómez E.; Hernández A. y Vázquez F. (999). The Esscher Premium Principle in isk Theory: a Bayesian Sensiiviy Sudy." Insurance: Mahemaics and Economics 5 (3) pp Heilmann W. (989). "Decision heoreic foundaions of credibiliy heory." Insurance: Mahemaics and Economics 8 pp
19 Heilmann W. y Schöer K. (987). On he robusness of premium principles. Insurance: Mahemaics and Economics 6 pp Herzog T. (994). Inroducion o Credibiliy Theory. ACTEX Publicaions Winsed. Hurlimann W. (994). A noe on experience raing reinsurance and premium principles. Insurance: Mahemaics and Economics 4 pp Klugmann S. Panjer H. y Willmo G. (988). Loss Models: From Daa o Decisions. John Wiley & Sond Inc. New York. Kuen S. y Yang H. (999). "Subjeive isk Measures: Bayesian Predicive Scenarios Analysis." Insurance: Mahemaics and Economics 5 pp Moreno E. y Cano J. (99). "obus Bayesian Analysis for ε -conaminaions parially known." Journal of he oyal Saisical. Series B 53 pp Sivaganesan S. (99). "Sensiiviy of some poserior summaries when he prior is unimodal wih specified quaniles." The Canadian Journal of Saisics Vol. 9 pp Sivaganesan S. y Berger J. (989). "anges of poserior measures for priors wih unimodal conaminaions." The Annals of Saisics Vol. 7 pp Young V. (999). Opimal insurance under Wang s premium principle. Insurance: Mahemaics and Economics 5 pp
Estudios de Economía Aplicada Asociación de Economía Aplicada, (ASEPELT) secretaria.tecnica@revista-eea.net ISSN: 1133-3197 ESPAÑA
 Esudios de Economía Aplicada Asociación de Economía Aplicada (ASEPELT) secrearia.ecnica@revisa-eea.ne ISSN: 33-397 ESPAÑA E. Gómez Déniz / J. M. Pérez Sánchez FIJACIÓN DE PRIMAS DE SEGUROS BAJO TÉCNICAS
Esudios de Economía Aplicada Asociación de Economía Aplicada (ASEPELT) secrearia.ecnica@revisa-eea.ne ISSN: 33-397 ESPAÑA E. Gómez Déniz / J. M. Pérez Sánchez FIJACIÓN DE PRIMAS DE SEGUROS BAJO TÉCNICAS
PROCESOS ESTOCÁSTICOS PROCESOS ESTOCÁSTICOS INTEGRAL ESTOCÁSTICA ECUACIONES DIFERENCIALES ESTOCASTICAS: LEMA DE ITO
 PROCESOS ESOCÁSICOS PROCESOS ESOCÁSICOS INEGRAL ESOCÁSICA ECUACIONES DIFERENCIALES ESOCASICAS: LEMA DE IO Procesos esocásicos Un proceso esocásico describe la evolución emporal de una variable aleaoria.
PROCESOS ESOCÁSICOS PROCESOS ESOCÁSICOS INEGRAL ESOCÁSICA ECUACIONES DIFERENCIALES ESOCASICAS: LEMA DE IO Procesos esocásicos Un proceso esocásico describe la evolución emporal de una variable aleaoria.
Métodos de Previsión de la Demanda Datos
 Daos Pronósico de la Demanda para Series Niveladas Esime la demanda a la que va a hacer frene la empresa "Don Pinzas". La información disponible para poder esablecer el pronósico de la demanda de ese produco
Daos Pronósico de la Demanda para Series Niveladas Esime la demanda a la que va a hacer frene la empresa "Don Pinzas". La información disponible para poder esablecer el pronósico de la demanda de ese produco
1.- ALGORITMOS RÁPIDOS PARA LA EJECUCIÓN DE FILTROS DE PILA
 hp://www.vinuesa.com 1.- ALGORITMOS RÁPIDOS PARA LA EJECUCIÓN DE FILTROS DE PILA 1.1.- INTRODUCCIÓN Los filros de pila consiuyen una clase de filros digiales no lineales. Un filro de pila que es usado
hp://www.vinuesa.com 1.- ALGORITMOS RÁPIDOS PARA LA EJECUCIÓN DE FILTROS DE PILA 1.1.- INTRODUCCIÓN Los filros de pila consiuyen una clase de filros digiales no lineales. Un filro de pila que es usado
Y t = Y t Y t-1. Y t plantea problemas a la hora de efectuar comparaciones entre series de valores de distintas variables.
 ASAS DE VARIACIÓN ( véase Inroducción a la Esadísica Económica y Empresarial. eoría y Pácica. Pág. 513-551. Marín Pliego, F. J. Ed. homson. Madrid. 2004) Un aspeco del mundo económico que es de gran inerés
ASAS DE VARIACIÓN ( véase Inroducción a la Esadísica Económica y Empresarial. eoría y Pácica. Pág. 513-551. Marín Pliego, F. J. Ed. homson. Madrid. 2004) Un aspeco del mundo económico que es de gran inerés
Modelo de regresión lineal simple
 Modelo de regresión lineal simple Inroducción Con frecuencia, nos enconramos en economía con modelos en los que el comporamieno de una variable,, se puede explicar a ravés de una variable X; lo que represenamos
Modelo de regresión lineal simple Inroducción Con frecuencia, nos enconramos en economía con modelos en los que el comporamieno de una variable,, se puede explicar a ravés de una variable X; lo que represenamos
Cobertura de una cartera de bonos con forwards en tiempo continuo
 Coberura de una carera de bonos con forwards en iempo coninuo Bàrbara Llacay Gilber Peffer Documeno de Trabajo IAFI No. 7/4 Marzo 23 Índice general Inroducción 2 Objeivos......................................
Coberura de una carera de bonos con forwards en iempo coninuo Bàrbara Llacay Gilber Peffer Documeno de Trabajo IAFI No. 7/4 Marzo 23 Índice general Inroducción 2 Objeivos......................................
Práctica 20. CARGA Y DESCARGA DE UN CONDENSADOR ELÉCTRICO
 Prácica 20. CARGA Y DESCARGA DE UN CONDENSADOR ELÉCTRICO OBJETIVOS Esudiar los procesos de carga y de descarga de un condensador. Medida de capacidades por el méodo de la consane de iempo. MATERIAL Generador
Prácica 20. CARGA Y DESCARGA DE UN CONDENSADOR ELÉCTRICO OBJETIVOS Esudiar los procesos de carga y de descarga de un condensador. Medida de capacidades por el méodo de la consane de iempo. MATERIAL Generador
TEMA 9: LA TASA NATURAL DE DESEMPLEO Y LA CURVA DE PHILLIPS
 TEMA 9: LA TASA NATURAL DE DESEMPLEO Y LA CURVA DE PHILLIPS 9.2 La asa naural de desempleo y la curva de Phillips La relación enre el desempleo y la inflación La curva de Phillips, basada en los daos aneriores
TEMA 9: LA TASA NATURAL DE DESEMPLEO Y LA CURVA DE PHILLIPS 9.2 La asa naural de desempleo y la curva de Phillips La relación enre el desempleo y la inflación La curva de Phillips, basada en los daos aneriores
3 Aplicaciones de primer orden
 CAÍTULO 3 Aplicaciones de primer orden 3.2. Modelo logísico El modelo de Malhus iene muchas limiaciones. or ejemplo, predice que una población crecerá exponencialmene con el iempo, que no ocurre en la
CAÍTULO 3 Aplicaciones de primer orden 3.2. Modelo logísico El modelo de Malhus iene muchas limiaciones. or ejemplo, predice que una población crecerá exponencialmene con el iempo, que no ocurre en la
El comportamiento del precio de las acciones
 El comporamieno del precio de las acciones Esrella Peroi Invesigador enior Bolsa de Comercio de Rosario eperoi@bcr.com.ar Para comprender el funcionamieno de los modelos de valuación de opciones sobre
El comporamieno del precio de las acciones Esrella Peroi Invesigador enior Bolsa de Comercio de Rosario eperoi@bcr.com.ar Para comprender el funcionamieno de los modelos de valuación de opciones sobre
Las derivadas de los instrumentos de renta fija
 Las derivadas de los insrumenos de rena fija Esrella Peroi, MBA Ejecuivo a cargo Capaciación & Desarrollo Bolsa de Comercio de Rosario eperoi@bcr.com.ar Como viéramos en el arículo el dilema enre la asa
Las derivadas de los insrumenos de rena fija Esrella Peroi, MBA Ejecuivo a cargo Capaciación & Desarrollo Bolsa de Comercio de Rosario eperoi@bcr.com.ar Como viéramos en el arículo el dilema enre la asa
Aplicaciones de la Probabilidad en la Industria
 Aplicaciones de la Probabilidad en la Indusria Cuara pare Final Dr Enrique Villa Diharce CIMAT, Guanajuao, México Verano de probabilidad y esadísica CIMAT Guanajuao,Go Julio 010 Reglas para deección de
Aplicaciones de la Probabilidad en la Indusria Cuara pare Final Dr Enrique Villa Diharce CIMAT, Guanajuao, México Verano de probabilidad y esadísica CIMAT Guanajuao,Go Julio 010 Reglas para deección de
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, CONCEPTOS BÁSICOS Y GRÁFICAS
 CINEMÁTICA: MOVIMIENTO RECTILÍNEO, CONCEPTOS BÁSICOS Y GRÁFICAS Dada la dependencia de la velocidad con la posición en un movimieno recilíneo mosrada por la siguiene gráfica, deerminar la dependencia con
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, CONCEPTOS BÁSICOS Y GRÁFICAS Dada la dependencia de la velocidad con la posición en un movimieno recilíneo mosrada por la siguiene gráfica, deerminar la dependencia con
Análisis de inversiones y proyectos de inversión
 Análisis de inversiones y proyecos de inversión Auora: Dra. Maie Seco Benedico Índice 5. Análisis de Inversiones 1. Inroducción. 2. Crierios para la valoración de un proyeco. 3. Técnicas de valoración
Análisis de inversiones y proyecos de inversión Auora: Dra. Maie Seco Benedico Índice 5. Análisis de Inversiones 1. Inroducción. 2. Crierios para la valoración de un proyeco. 3. Técnicas de valoración
Capítulo 5 Sistemas lineales de segundo orden
 Capíulo 5 Sisemas lineales de segundo orden 5. Definición de sisema de segundo orden Un sisema de segundo orden es aquel cuya salida y puede ser descria por una ecuación diferencial de segundo orden: d
Capíulo 5 Sisemas lineales de segundo orden 5. Definición de sisema de segundo orden Un sisema de segundo orden es aquel cuya salida y puede ser descria por una ecuación diferencial de segundo orden: d
UNA MODELIZACIÓN PARA LOS ACCIDENTES DE TRABAJO EN ESPAÑA Y ANDALUCÍA
 UNA MODELIZACIÓN PARA LOS ACCIDENTES DE TRABAJO EN ESPAÑA Y ANDALUCÍA Por Mónica Orega Moreno Profesora Esadísica. Deparameno Economía General y Esadísica RESUMEN El aumeno de la siniesralidad laboral
UNA MODELIZACIÓN PARA LOS ACCIDENTES DE TRABAJO EN ESPAÑA Y ANDALUCÍA Por Mónica Orega Moreno Profesora Esadísica. Deparameno Economía General y Esadísica RESUMEN El aumeno de la siniesralidad laboral
METODOLOGÍA PARA EL AJUSTE DE LAS TASAS DE ESCOLARIZACIÓN A PARTIR DE LA INFORMACIÓN DEL CENSO NACIONAL DE POBLACIÓN, HOGARES Y VIVIENDA DE 2001
 METODOLOGÍA PARA EL AJUSTE DE LAS TASAS DE ESCOLARIZACIÓN A PARTIR DE LA INFORMACIÓN DEL CENSO NACIONAL DE POBLACIÓN, HOGARES Y VIVIENDA DE 2001 Insiuo Nacional de Esadísica y Censos (INDEC) Dirección
METODOLOGÍA PARA EL AJUSTE DE LAS TASAS DE ESCOLARIZACIÓN A PARTIR DE LA INFORMACIÓN DEL CENSO NACIONAL DE POBLACIÓN, HOGARES Y VIVIENDA DE 2001 Insiuo Nacional de Esadísica y Censos (INDEC) Dirección
Ecuaciones diferenciales, conceptos básicos y aplicaciones
 GUIA 1 Ecuaciones diferenciales, concepos básicos y aplicaciones Las ecuaciones diferenciales ordinarias son una herramiena básica en las ciencias y las ingenierías para el esudio de sisemas dinámicos
GUIA 1 Ecuaciones diferenciales, concepos básicos y aplicaciones Las ecuaciones diferenciales ordinarias son una herramiena básica en las ciencias y las ingenierías para el esudio de sisemas dinámicos
MACROECONOMIA II. Grado Economía 2013-2014
 MACROECONOMIA II Grado Economía 2013-2014 PARTE II: FUNDAMENTOS MICROECONÓMICOS DE LA MACROECONOMÍA 3 4 5 Tema 2 Las expecaivas: los insrumenos básicos De qué dependen las decisiones económicas? Tipo de
MACROECONOMIA II Grado Economía 2013-2014 PARTE II: FUNDAMENTOS MICROECONÓMICOS DE LA MACROECONOMÍA 3 4 5 Tema 2 Las expecaivas: los insrumenos básicos De qué dependen las decisiones económicas? Tipo de
Master en Economía Macroeconomía II. 1 Problema de Ahorro-Consumo en Horizonte Finito
 Maser en Economía Macroeconomía II Profesor: Danilo Trupkin Se de Problemas 1 - Soluciones 1 Problema de Ahorro-Consumo en Horizone Finio Considere un problema de ahorro-consumo sobre un horizone finio
Maser en Economía Macroeconomía II Profesor: Danilo Trupkin Se de Problemas 1 - Soluciones 1 Problema de Ahorro-Consumo en Horizone Finio Considere un problema de ahorro-consumo sobre un horizone finio
Investigación y Técnicas de Mercado. Previsión de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE.
 Invesigación y écnicas de Mercado Previsión de Venas ÉCNICAS CUANIAIVAS ELEMENALES DE PREVISIÓN UNIVARIANE. (II) écnicas elemenales: Modelos Naive y Medias Móviles. Medición del error de previsión. Profesor:
Invesigación y écnicas de Mercado Previsión de Venas ÉCNICAS CUANIAIVAS ELEMENALES DE PREVISIÓN UNIVARIANE. (II) écnicas elemenales: Modelos Naive y Medias Móviles. Medición del error de previsión. Profesor:
Keywords: seguro de vida, provisión matemática, probabilidad, función de distribución, solvencia, value at risk, VAT, valor actual neto, VAN.
 El seguro de vida como variable aleaoria. Cómo calcular su función de disribución. Nieo Ranero, Armando Universiy of Valencia, Spain Do. Maemáicas Económico Empresarial, Edificio Deparamenal Orienal, Av.
El seguro de vida como variable aleaoria. Cómo calcular su función de disribución. Nieo Ranero, Armando Universiy of Valencia, Spain Do. Maemáicas Económico Empresarial, Edificio Deparamenal Orienal, Av.
TEMA 1 INTRODUCCIÓN A LA ELECTRÓNICA DIGITAL. 1. Sistemas analógicos y digitales.
 T-1 Inroducción a la elecrónica digial 1 TEMA 1 INTRODUCCIÓN A LA ELECTRÓNICA DIGITAL El raamieno de la información en elecrónica se puede realizar de dos formas, mediane écnicas analógicas o mediane écnicas
T-1 Inroducción a la elecrónica digial 1 TEMA 1 INTRODUCCIÓN A LA ELECTRÓNICA DIGITAL El raamieno de la información en elecrónica se puede realizar de dos formas, mediane écnicas analógicas o mediane écnicas
TEMA I: FUNCIONES ELEMENTALES
 TEMA I: FUNCIONES ELEMENTALES. Función Logarimo Todos conocemos la definición de logarimo en base b, siendo b un número enero posiivo disino de. u = log b x x = b u y la propiedad fundamenal log b (xy)
TEMA I: FUNCIONES ELEMENTALES. Función Logarimo Todos conocemos la definición de logarimo en base b, siendo b un número enero posiivo disino de. u = log b x x = b u y la propiedad fundamenal log b (xy)
Foundations of Financial Management Page 1
 Foundaions of Financial Managemen Page 1 Combinaciones empresarias: decisiones sobre absorciones y fusiones de empresas Adminisración financiera UNLPam Faculad de Ciencias Económicas y Jurídicas Profesor:
Foundaions of Financial Managemen Page 1 Combinaciones empresarias: decisiones sobre absorciones y fusiones de empresas Adminisración financiera UNLPam Faculad de Ciencias Económicas y Jurídicas Profesor:
Master en Economía Macroeconomía II. 1 Learning by Doing (versión en tiempo discreto)
 Maser en Economía Macroeconomía II Profesor: Danilo Trupkin Se de Problemas 4 - Soluciones 1 Learning by Doing (versión en iempo discreo) Considere una economía cuyas preferencias, ecnología, y acumulación
Maser en Economía Macroeconomía II Profesor: Danilo Trupkin Se de Problemas 4 - Soluciones 1 Learning by Doing (versión en iempo discreo) Considere una economía cuyas preferencias, ecnología, y acumulación
Guía de Ejercicios Econometría II Ayudantía Nº 3
 Guía de Ejercicios Economería II Ayudanía Nº 3 1.- La serie del dao hisórico del IPC Español desde enero de 2002 hasa diciembre de 2011, esá represenada en el siguiene gráfico: 115 110 105 100 95 90 85
Guía de Ejercicios Economería II Ayudanía Nº 3 1.- La serie del dao hisórico del IPC Español desde enero de 2002 hasa diciembre de 2011, esá represenada en el siguiene gráfico: 115 110 105 100 95 90 85
RE01 DIFERENCIA DEL LOGRO PROMEDIO EN COMPRENSIÓN LECTORA Y MATEMÁTICAS PARA 6 DE PRIMARIA Y 3 DE SECUNDARIA ENTRE 2000 Y 2005
 RESULTADOSEDUCATIVOS RE01 DIFERENCIA DEL LOGRO PROMEDIO EN COMPRENSIÓN LECTORA Y MATEMÁTICAS PARA 6 DE PRIMARIA Y 3 DE SECUNDARIA ENTRE 2000 Y 2005 FÓRMULA RE01 NOMBREdelINDICADOR Diferencia del loro promedio
RESULTADOSEDUCATIVOS RE01 DIFERENCIA DEL LOGRO PROMEDIO EN COMPRENSIÓN LECTORA Y MATEMÁTICAS PARA 6 DE PRIMARIA Y 3 DE SECUNDARIA ENTRE 2000 Y 2005 FÓRMULA RE01 NOMBREdelINDICADOR Diferencia del loro promedio
1 Introducción... 2. 2 Tiempo de vida... 3. 3 Función de fiabilidad... 4. 4 Vida media... 6. 5 Tasa de fallo... 9. 6 Relación entre conceptos...
 Asignaura: Ingeniería Indusrial Índice de Conenidos 1 Inroducción... 2 2 Tiempo de vida... 3 3 Función de fiabilidad... 4 4 Vida media... 6 5 Tasa de fallo... 9 6 Relación enre concepos... 12 7 Observaciones
Asignaura: Ingeniería Indusrial Índice de Conenidos 1 Inroducción... 2 2 Tiempo de vida... 3 3 Función de fiabilidad... 4 4 Vida media... 6 5 Tasa de fallo... 9 6 Relación enre concepos... 12 7 Observaciones
Metodología de cálculo del diferencial base
 Meodología de cálculo del diferencial base El diferencial base es el resulado de expresar los gasos generales promedio de operación de las insiuciones de seguros auorizadas para la prácica de los Seguros
Meodología de cálculo del diferencial base El diferencial base es el resulado de expresar los gasos generales promedio de operación de las insiuciones de seguros auorizadas para la prácica de los Seguros
Nota Técnica Índice de Tipo de Cambio Efectivo Real Multilateral con ponderadores móviles
 Noa Técnica Índice de Tipo de Cambio Efecivo Real Mulilaeral con ponderadores móviles 1. Inroducción: La presene noa écnica preende inroducir y explicar al público el Índice de Tipo de Cambio Efecivo Real
Noa Técnica Índice de Tipo de Cambio Efecivo Real Mulilaeral con ponderadores móviles 1. Inroducción: La presene noa écnica preende inroducir y explicar al público el Índice de Tipo de Cambio Efecivo Real
Examen Parcial de Econometría II. Nombre: RESOLUCION DEL EXAMEN PARCIAL Paralelo:
 Escuela Superior Poliécnica del Lioral Faculad de Economía y Negocios 30-11-2011 Examen Parcial de Economería II Nombre: RESOLUCION DEL EXAMEN PARCIAL Paralelo: REGLAMENTO DE EVALUACIONES Y CALIFICACIONES
Escuela Superior Poliécnica del Lioral Faculad de Economía y Negocios 30-11-2011 Examen Parcial de Economería II Nombre: RESOLUCION DEL EXAMEN PARCIAL Paralelo: REGLAMENTO DE EVALUACIONES Y CALIFICACIONES
Test. Cada pregunta correcta está valorada con 0.5 puntos y cada incorrecta resta 0.25 puntos
 Teléf.: 91 533 38 4-91 535 19 3 8003 MADRID EXAMEN DE ECONOMETRÍA (enero 010) 1h 15 Apellidos: Nombre: Tes. Cada preguna correca esá valorada con 0.5 punos y cada incorreca resa 0.5 punos 1.- Al conrasar
Teléf.: 91 533 38 4-91 535 19 3 8003 MADRID EXAMEN DE ECONOMETRÍA (enero 010) 1h 15 Apellidos: Nombre: Tes. Cada preguna correca esá valorada con 0.5 punos y cada incorreca resa 0.5 punos 1.- Al conrasar
ACTIVIDADES UNIDAD 7: Funciones elementales
 ACTIVIDADES UNIDAD 7: Funciones elemenales 1. La facura del gas de una familia, en sepiembre, fue de 4,8 euros por 1 m 3, y en ocubre, de 43,81 por 4 m 3. a) Escribe la función que da el impore de la facura
ACTIVIDADES UNIDAD 7: Funciones elemenales 1. La facura del gas de una familia, en sepiembre, fue de 4,8 euros por 1 m 3, y en ocubre, de 43,81 por 4 m 3. a) Escribe la función que da el impore de la facura
PRÁCTICA 3: Sistemas de Orden Superior:
 PRÁCTICA 3: Sisemas de Orden Superior: Idenificación de modelo de POMTM. Esabilidad y Régimen Permanene de Sisemas Realimenados Conrol e Insrumenación de Procesos Químicos. . INTRODUCCIÓN Esa prácica se
PRÁCTICA 3: Sisemas de Orden Superior: Idenificación de modelo de POMTM. Esabilidad y Régimen Permanene de Sisemas Realimenados Conrol e Insrumenación de Procesos Químicos. . INTRODUCCIÓN Esa prácica se
MATEMATICAS I FUNCIONES ELEMENTALES. PROBLEMAS
 1º) La facura del gas se calcula a parir de una canidad fija y de un canidad variable que se calcula según los m 3 consumidos (el precio de cada m 3 es consane). El impore de la facura de una familia,
1º) La facura del gas se calcula a parir de una canidad fija y de un canidad variable que se calcula según los m 3 consumidos (el precio de cada m 3 es consane). El impore de la facura de una familia,
13.0 COSTOS Y VALORACIÓN ECONÓMICA
 13.0 COSTOS Y VALORACIÓN ECONÓMICA 13.1 INTRODUCCIÓN En esa sección, se calcula el valor económico de los impacos ambienales que generará el Proyeco Cruce Aéreo de la Fibra Ópica en el Kp 184+900, el cual
13.0 COSTOS Y VALORACIÓN ECONÓMICA 13.1 INTRODUCCIÓN En esa sección, se calcula el valor económico de los impacos ambienales que generará el Proyeco Cruce Aéreo de la Fibra Ópica en el Kp 184+900, el cual
La transformada de Laplace
 Capíulo 8 La ransformada de Laplace 8.. Inroducción a las ransformadas inegrales En ese aparado aprenderemos un méodo alernaivo para resolver el problema de valores iniciales (4.5.) y (x) + py (x) + qy(x)
Capíulo 8 La ransformada de Laplace 8.. Inroducción a las ransformadas inegrales En ese aparado aprenderemos un méodo alernaivo para resolver el problema de valores iniciales (4.5.) y (x) + py (x) + qy(x)
La Conducción de la Política Monetaria del Banco de México a través del Régimen de Saldos Diarios
 La Conducción de la Políica Monearia del Banco de México a ravés del Régimen de Saldos Diarios INDICE I. INTRODUCCIÓN...2 II. LA OPERACIÓN DEL BANCO DE MÉXICO EN EL MERCADO DE DINERO...3 III. IV. II.1.
La Conducción de la Políica Monearia del Banco de México a ravés del Régimen de Saldos Diarios INDICE I. INTRODUCCIÓN...2 II. LA OPERACIÓN DEL BANCO DE MÉXICO EN EL MERCADO DE DINERO...3 III. IV. II.1.
MEDICIÓ N DEL VALOR ECONÓ MICO AGREGADO: INVERSIÓ N RECUPERADA Y VALOR AGREGADO IRVA
 MEDICIÓ N DEL VALOR ECONÓ MICO AGREGADO: INVERSIÓ N RECUPERADA Y VALOR AGREGADO IRVA (Borrador) Ignacio Vélez-Pareja Deparameno de Adminisración Universidad Javeriana, Bogoá, Colombia Abril de 2000 Resumen
MEDICIÓ N DEL VALOR ECONÓ MICO AGREGADO: INVERSIÓ N RECUPERADA Y VALOR AGREGADO IRVA (Borrador) Ignacio Vélez-Pareja Deparameno de Adminisración Universidad Javeriana, Bogoá, Colombia Abril de 2000 Resumen
Técnicas cualitativas para las Ecuaciones diferenciales de primer orden: Campos de pendientes y líneas de fase
 Lección 5 Técnicas cualiaivas para las Ecuaciones diferenciales de primer orden: Campos de pendienes y líneas de fase 5.. Técnicas Cualiaivas Hasa ahora hemos esudiado écnicas analíicas para calcular,
Lección 5 Técnicas cualiaivas para las Ecuaciones diferenciales de primer orden: Campos de pendienes y líneas de fase 5.. Técnicas Cualiaivas Hasa ahora hemos esudiado écnicas analíicas para calcular,
RESOLUCIÓN 34-03 SOBRE COMISIONES DE LAS ADMINISTRADORAS DE FONDOS DE PENSIONES
 RESOLUCIÓN 34-03 SOBRE COMISIONES DE LAS ADMINISTRADORAS DE FONDOS DE PENSIONES CONSIDERANDO: Que el arículo 86 de la Ley 87-01 de fecha 9 de mayo de 2001, que crea el Sisema Dominicano de Seguridad Social,
RESOLUCIÓN 34-03 SOBRE COMISIONES DE LAS ADMINISTRADORAS DE FONDOS DE PENSIONES CONSIDERANDO: Que el arículo 86 de la Ley 87-01 de fecha 9 de mayo de 2001, que crea el Sisema Dominicano de Seguridad Social,
Tema 5: Diferenciabilidad: Aplicaciones
 Prof. Susana López 1 UniversidadAuónomadeMadrid Tema 5: Diferenciabilidad: Aplicaciones 1 Funciones compuesas y Regla de la cadena Recordemos que la regla de la cadena para funciones de una sola variable
Prof. Susana López 1 UniversidadAuónomadeMadrid Tema 5: Diferenciabilidad: Aplicaciones 1 Funciones compuesas y Regla de la cadena Recordemos que la regla de la cadena para funciones de una sola variable
Solvencia II. Los Conceptos Básicos. Por: P. Aguilar. Febrero de 2008
 Solvencia II Los Concepos Básicos Por: P. Aguilar Febrero de 2008 El esquema regulaorio de Solvencia II planea un impaco relevane en el ejercicio de la prácica acuarial. Tal esquema se caraceriza por descansar
Solvencia II Los Concepos Básicos Por: P. Aguilar Febrero de 2008 El esquema regulaorio de Solvencia II planea un impaco relevane en el ejercicio de la prácica acuarial. Tal esquema se caraceriza por descansar
J.1. Análisis de la rentabilidad del proyecto... 3
 Esudio de la implanación de una unidad produciva dedicada a la Pág 1 abricación de conjunos soldados de aluminio J.1. Análisis de la renabilidad del proyeco... 3 J.1.1. Desglose del proyeco en coses ijos
Esudio de la implanación de una unidad produciva dedicada a la Pág 1 abricación de conjunos soldados de aluminio J.1. Análisis de la renabilidad del proyeco... 3 J.1.1. Desglose del proyeco en coses ijos
Departamento de Psicología Social y Organizacional
 universidad caólica del uruguay anuario de acividades de invesigación 2010 135 Deparameno de Psicología Social y Organizacional Aciudes, idenidades y esereoipos nacionales y supranacionales. Invesigador:
universidad caólica del uruguay anuario de acividades de invesigación 2010 135 Deparameno de Psicología Social y Organizacional Aciudes, idenidades y esereoipos nacionales y supranacionales. Invesigador:
Dispositivos semiconductores
 Deparameno de Telecomunicaciones Disposiivos semiconducores 3 Inroduccion Veremos los disposiivos semiconducores más básicos: los diodos. Veremos las variables más comunes de esos semiconducores; El diodo
Deparameno de Telecomunicaciones Disposiivos semiconducores 3 Inroduccion Veremos los disposiivos semiconducores más básicos: los diodos. Veremos las variables más comunes de esos semiconducores; El diodo
Modelos de Ajuste Nominal Incompleto. Por Agustín Casas, UdeSa. Diego Hofman, Princeton. Analía Olgiati, BID. Javier DiFiori, Morgan Stanley
 Modelos de Ajuse Nominal Incompleo Por Agusín Casas, UdeSa. Diego Hofman, Princeon. Analía Olgiai, BID. Javier DiFiori, Morgan Sanley JEL CLASS: E12 - Keynes; Keynesian; Pos-Keynesian E13 - Neoclassical
Modelos de Ajuse Nominal Incompleo Por Agusín Casas, UdeSa. Diego Hofman, Princeon. Analía Olgiai, BID. Javier DiFiori, Morgan Sanley JEL CLASS: E12 - Keynes; Keynesian; Pos-Keynesian E13 - Neoclassical
IGEP Tema 2. Leyas financieras básicas: estudio usando aplicaciones informáticas.
 IGEP Tema 2. Leyas financieras básicas: esudio usando aplicaciones informáicas. onenido. apial financiero... 2. Leyes financieras: capialización y descueno...4 2. Leyes de capialización...4 2.2 Leyes de
IGEP Tema 2. Leyas financieras básicas: esudio usando aplicaciones informáicas. onenido. apial financiero... 2. Leyes financieras: capialización y descueno...4 2. Leyes de capialización...4 2.2 Leyes de
UNA APROXIMACION A LA SOSTENIBILIDAD FISCAL EN REPUBLICA DOMINICANA Juan Temístocles Montás
 UNA APROXIMACION A LA SOSTENIBILIDAD FISCAL EN REPUBLICA DOMINICANA Juan Temísocles Monás Puede el comporamieno acual de la políica fiscal sosenerse sin generar una deuda pública que crezca sin límie?
UNA APROXIMACION A LA SOSTENIBILIDAD FISCAL EN REPUBLICA DOMINICANA Juan Temísocles Monás Puede el comporamieno acual de la políica fiscal sosenerse sin generar una deuda pública que crezca sin límie?
Control de un péndulo invertido usando métodos de diseño no lineales
 Conrol de un péndulo inverido usando méodos de diseño no lineales F. Salas salas@caruja.us.es J.Aracil aracil@esi.us.es F. Gordillo gordillo@esi.us.es Depo de Ingeniería de Sisemas y Auomáica.Escuela Superior
Conrol de un péndulo inverido usando méodos de diseño no lineales F. Salas salas@caruja.us.es J.Aracil aracil@esi.us.es F. Gordillo gordillo@esi.us.es Depo de Ingeniería de Sisemas y Auomáica.Escuela Superior
Capítulo 4 Sistemas lineales de primer orden
 Capíulo 4 Sisemas lineales de primer orden 4. Definición de sisema lineal de primer orden Un sisema de primer orden es aquel cuya salida puede ser modelada por una ecuación diferencial de primer orden
Capíulo 4 Sisemas lineales de primer orden 4. Definición de sisema lineal de primer orden Un sisema de primer orden es aquel cuya salida puede ser modelada por una ecuación diferencial de primer orden
LÍNEAS DE FASES. Fig. 1. dx (1) dt se llama Ecuación Diferencial Ordinaria (E.D.O.) de Primer Orden definida en Ω.
 LÍNEAS DE FASES E. SÁEZ Sea el dominio Ω R R y la función F : Ω R. F R Ω Una epresión de la forma Fig. 1 d (1) = F(,), o bien, ẋ = F(,) se llama Ecuación Diferencial Ordinaria (E.D.O.) de Primer Orden
LÍNEAS DE FASES E. SÁEZ Sea el dominio Ω R R y la función F : Ω R. F R Ω Una epresión de la forma Fig. 1 d (1) = F(,), o bien, ẋ = F(,) se llama Ecuación Diferencial Ordinaria (E.D.O.) de Primer Orden
TEMA 2 MODELO LINEAL SIMPLE (MLS) Gujarati, Econometria (2004)
 EMA 2 MODELO LINEAL SIMPLE (MLS) Gujarai, Economeria (2004). Planeamieno e inerpreación del modelo economérico lineal simple. Capíulo 2 páginas 36 a 39 2. Hipóesis Básicas del Modelo Capíulo 3 páginas
EMA 2 MODELO LINEAL SIMPLE (MLS) Gujarai, Economeria (2004). Planeamieno e inerpreación del modelo economérico lineal simple. Capíulo 2 páginas 36 a 39 2. Hipóesis Básicas del Modelo Capíulo 3 páginas
TEMA: FUNCIONES: Cuadrantes 3 er cuadrante, x 0, 4º cuadrante, x 0,
 TEMA: FUNCIONES: ÍNDICE:. Inroducción.. Dominio y recorrido.. Gráficas de funciones elemenales. Funciones definidas a rozos. 4. Coninuidad.. Crecimieno y decrecimieno, máimos y mínimos. 6. Concavidad y
TEMA: FUNCIONES: ÍNDICE:. Inroducción.. Dominio y recorrido.. Gráficas de funciones elemenales. Funciones definidas a rozos. 4. Coninuidad.. Crecimieno y decrecimieno, máimos y mínimos. 6. Concavidad y
Sistemade indicadores compuestos coincidentey adelantado julio,2010
 Sisemade indicadores compuesos coincideney adelanado julio,2010 Sisema de Indicadores Compuesos: Coincidene y Adelanado SI REQUIERE INFORMACIÓN MÁS DETALLADA DE ESTA OBRA, FAVOR DE COMUNICARSE A: Insiuo
Sisemade indicadores compuesos coincideney adelanado julio,2010 Sisema de Indicadores Compuesos: Coincidene y Adelanado SI REQUIERE INFORMACIÓN MÁS DETALLADA DE ESTA OBRA, FAVOR DE COMUNICARSE A: Insiuo
TEMA 2 LOS MODELOS ECONOMETRICOS Y SU PROBLEMATICA
 TEMA 2 LOS MODELOS ECONOMETRICOS Y SU PROBLEMATICA 1. CONCEPTO DE MODELO El ermino modelo debe de idenificarse con un esquema menal ya que es una represenación de la realidad. En ese senido, Pulido (1983)
TEMA 2 LOS MODELOS ECONOMETRICOS Y SU PROBLEMATICA 1. CONCEPTO DE MODELO El ermino modelo debe de idenificarse con un esquema menal ya que es una represenación de la realidad. En ese senido, Pulido (1983)
INSTITUTO NACIONAL DE PESCA
 INSTITUTO NACIONAL DE PESCA Dirección General de Invesigación Pesquera en el Pacífico Nore Subdirección de Tecnología en el Pacífico Nore. Indicadores económico-financieros para la capura de camarón y
INSTITUTO NACIONAL DE PESCA Dirección General de Invesigación Pesquera en el Pacífico Nore Subdirección de Tecnología en el Pacífico Nore. Indicadores económico-financieros para la capura de camarón y
TEMA 3 EXPECTATIVAS, CONSUMO E INVERSIÓN
 TEMA 3 EXPECTATIVAS, CONSUMO E INVERSIÓN En el Tema 2 analizamos el papel de las expecaivas en los mercados financieros. En ése nos cenraremos en los de bienes y servicios. El papel que desempeñan las
TEMA 3 EXPECTATIVAS, CONSUMO E INVERSIÓN En el Tema 2 analizamos el papel de las expecaivas en los mercados financieros. En ése nos cenraremos en los de bienes y servicios. El papel que desempeñan las
Representación gráfica de curvas en forma paramétrica x a(t sent) 1.- Representar la curva dada por
 Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
PROBLEMAS RESUELTOS 1 (continuidad, derivabilidad y diferenciabilidad de funciones de varias variables)
 Funciones de varias variables. PROBLEMAS RESUELTOS 1 (coninuidad, derivabilidad y diferenciabilidad de funciones de varias variables) PROBLEMA 1 Esudiar la coninuidad de la función: xy ( xy, ) (,) x +
Funciones de varias variables. PROBLEMAS RESUELTOS 1 (coninuidad, derivabilidad y diferenciabilidad de funciones de varias variables) PROBLEMA 1 Esudiar la coninuidad de la función: xy ( xy, ) (,) x +
Introducción a la Estadística Empresarial. Capítulo 4.- Series temporales Jesús Sánchez Fernández
 Inroducción a la Esadísica Empresarial. Capíulo 4.- Series emporales CAPITULO 4.- SERIES TEMPORALES 4. Inroducción. Hasa ahora odas las variables que se han esudiado enían en común que, por lo general,
Inroducción a la Esadísica Empresarial. Capíulo 4.- Series emporales CAPITULO 4.- SERIES TEMPORALES 4. Inroducción. Hasa ahora odas las variables que se han esudiado enían en común que, por lo general,
Solución: El sistema de referencia, la posición del cuerpo en cada instante respecto a dicha referencia, el tiempo empleado y la trayectoria seguida.
 1 Qué es necesario señalar para describir correcamene el movimieno de un cuerpo? El sisema de referencia, la posición del cuerpo en cada insane respeco a dicha referencia, el iempo empleado y la rayecoria
1 Qué es necesario señalar para describir correcamene el movimieno de un cuerpo? El sisema de referencia, la posición del cuerpo en cada insane respeco a dicha referencia, el iempo empleado y la rayecoria
UNIDAD IX. Técnicas de Suavización
 UNIDAD IX Técnicas de Suavización UNIDAD IX La esadísica demuesra que suele ser más fácil hacer algo bien que explicar por qué se hizo mal. Allen L. Webser, 1998 Cuál es el objeivo de la Técnica de suavización?
UNIDAD IX Técnicas de Suavización UNIDAD IX La esadísica demuesra que suele ser más fácil hacer algo bien que explicar por qué se hizo mal. Allen L. Webser, 1998 Cuál es el objeivo de la Técnica de suavización?
domótico Extras 2.1 Unidad de control 2.2 Dispositivos de entrada 2.4 Electrodomésticos domóticos 2.5 Medios de comunicación en redes domésticas
 2 Elemenos de un sisema domóico Conenidos 2.1 Unidad de conrol 2.2 Disposiivos de enrada 2.3 Acuadores 2.4 Elecrodomésicos domóicos 2.5 Medios de comunicación en redes domésicas 2.6 Tecnologías aplicadas
2 Elemenos de un sisema domóico Conenidos 2.1 Unidad de conrol 2.2 Disposiivos de enrada 2.3 Acuadores 2.4 Elecrodomésicos domóicos 2.5 Medios de comunicación en redes domésicas 2.6 Tecnologías aplicadas
Sus experiencias con el cáncer
 Número de OMB: 0935-0118 Fecha de vencimieno de la aprobación: 01/31/2013 Sus experiencias con el cáncer l Esa encuesa es acerca de las secuelas o efecos secundarios del cáncer y de los raamienos para
Número de OMB: 0935-0118 Fecha de vencimieno de la aprobación: 01/31/2013 Sus experiencias con el cáncer l Esa encuesa es acerca de las secuelas o efecos secundarios del cáncer y de los raamienos para
DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS
 DEPARTAMETO DE QUÍMICA AALÍTICA Y TECOLOGÍA DE ALIMETOS FUDAMETOS DE AÁLISIS ISTRUMETAL. 7º RELACIÓ DE PROBLEMAS..- Las susancias A y B ienen iempos de reención de 6.4 y 7.63 min, respecivamene, en una
DEPARTAMETO DE QUÍMICA AALÍTICA Y TECOLOGÍA DE ALIMETOS FUDAMETOS DE AÁLISIS ISTRUMETAL. 7º RELACIÓ DE PROBLEMAS..- Las susancias A y B ienen iempos de reención de 6.4 y 7.63 min, respecivamene, en una
{ 3} Nota. La raíz no impone condiciones al dominio por ser de índice impar.
 . Esudia el dominio de las siguienes unciones: a ( : Función Racional, el dominio son odos los números reales ecepo los que anulen el denominador. R / 0 : 0 : : ± [ ( ] { } R ± { } b ( : Función Racional,
. Esudia el dominio de las siguienes unciones: a ( : Función Racional, el dominio son odos los números reales ecepo los que anulen el denominador. R / 0 : 0 : : ± [ ( ] { } R ± { } b ( : Función Racional,
4.7. Integración de Word y Excel
 47 Inegración de Word y Excel 471 Combinar correspondencia Qué procedimieno seguiría para hacer las siguienes areas? Generar una cara de soliciud de permiso de los padres de familia para cada uno de sus
47 Inegración de Word y Excel 471 Combinar correspondencia Qué procedimieno seguiría para hacer las siguienes areas? Generar una cara de soliciud de permiso de los padres de familia para cada uno de sus
= Δx 2. Escogiendo un sistema de referencia común para ambos móviles x A
 Ejemplos de solución a problemas de Cinemáica de la parícula Diseño en PDF MSc. Carlos Álvarez Marínez de Sanelices, Dpo. Física, Universidad de Camagüey. Carlos.alvarez@reduc.edu.cu Acividad # C1. Un
Ejemplos de solución a problemas de Cinemáica de la parícula Diseño en PDF MSc. Carlos Álvarez Marínez de Sanelices, Dpo. Física, Universidad de Camagüey. Carlos.alvarez@reduc.edu.cu Acividad # C1. Un
MÉTODO DE DEFLACIÓN DE VARIABLES ECONÓMICAS: CUENTAS ECONÓMICAS Y TABLAS INPUT-OUTPUT CRISTINA PRADO
 MÉTODO DE DEFLACIÓN DE VARIABLES ECONÓMICAS: CUENTAS ECONÓMICAS Y TABLAS INPUT-OUTPUT CRISTINA PRADO EUSKAL ESTATISTIKA ERAKUNDEA INSTITUTO VASCO DE ESTADISTICA Donosia-San Sebasián, 1 01010 VITORIA-GASTEIZ
MÉTODO DE DEFLACIÓN DE VARIABLES ECONÓMICAS: CUENTAS ECONÓMICAS Y TABLAS INPUT-OUTPUT CRISTINA PRADO EUSKAL ESTATISTIKA ERAKUNDEA INSTITUTO VASCO DE ESTADISTICA Donosia-San Sebasián, 1 01010 VITORIA-GASTEIZ
Guías y tutoriales/compresores/winrar
 g coordinación de uoriales: Graciela Sosisky exo: Horacio Marínez Philipps edición: Gabriela Tenner diseño: CAFE Guías y uoriales/compresores/winrar Los orígenes de ese programa se remonan a las experiencias
g coordinación de uoriales: Graciela Sosisky exo: Horacio Marínez Philipps edición: Gabriela Tenner diseño: CAFE Guías y uoriales/compresores/winrar Los orígenes de ese programa se remonan a las experiencias
6 METODOLOGÍA PROPUESTA PARA VALORAR USOS IN SITU DEL AGUA
 38 6 METODOLOGÍA PROPUESTA PARA VALORAR USOS IN SITU DEL AGUA 6.1 Méodo general Para valorar los usos recreacionales del agua, se propone una meodología por eapas que combina el uso de diferenes écnicas
38 6 METODOLOGÍA PROPUESTA PARA VALORAR USOS IN SITU DEL AGUA 6.1 Méodo general Para valorar los usos recreacionales del agua, se propone una meodología por eapas que combina el uso de diferenes écnicas
Mtro. Horacio Catalán Alonso
 ECONOMETRIA TEORÍA DE LA COINTEGRACIÓN Mro. I. REGRESIÓN ESPURÍA Y X Dos series que presenan camino aleaorio. Si ambas series se consideran en una modelo economérico. Y = Y -1 + u u N(0,s 2 u) X =X -1
ECONOMETRIA TEORÍA DE LA COINTEGRACIÓN Mro. I. REGRESIÓN ESPURÍA Y X Dos series que presenan camino aleaorio. Si ambas series se consideran en una modelo economérico. Y = Y -1 + u u N(0,s 2 u) X =X -1
Aplicación de la teoría de Opciones Reales al Análisis de Inversiones en Nuevas Tecnologías *. 41092 Sevilla, pedroluis@esi.us.
 ƒ Índice Aplicación de la eoría de Opciones Reales al Análisis de Inversiones en Nuevas ecnologías *. José Miguel León Blanco 1, José Manuel Framiñán orres 2, Rafael Ruiz Usano 3, Pedro Luis González Rodríguez
ƒ Índice Aplicación de la eoría de Opciones Reales al Análisis de Inversiones en Nuevas ecnologías *. José Miguel León Blanco 1, José Manuel Framiñán orres 2, Rafael Ruiz Usano 3, Pedro Luis González Rodríguez
FUNCIONES VECTORIALES CON DERIVE.
 FUNCIONES VECTORIALES CON DERIVE. Las operaciones de cálculo de Dominio, adición susracción, muliplicación escalar y vecorial de funciones vecoriales, se realizan de manera similar a las operaciones con
FUNCIONES VECTORIALES CON DERIVE. Las operaciones de cálculo de Dominio, adición susracción, muliplicación escalar y vecorial de funciones vecoriales, se realizan de manera similar a las operaciones con
UD: 3. ENERGÍA Y POTENCIA ELÉCTRICA.
 D: 3. ENEGÍA Y OENCA ELÉCCA. La energía es definida como la capacidad de realizar rabajo y relacionada con el calor (ransferencia de energía), se percibe fundamenalmene en forma de energía cinéica, asociada
D: 3. ENEGÍA Y OENCA ELÉCCA. La energía es definida como la capacidad de realizar rabajo y relacionada con el calor (ransferencia de energía), se percibe fundamenalmene en forma de energía cinéica, asociada
3. Matrices y álgebra matricial
 Marices y álgebra maricial Repasaremos algunos concepos básicos de la eoría maricial Nos cenraremos en aspecos relacionados con el álgebra lineal, la inversión y la diagonalización de marices Veremos algunas
Marices y álgebra maricial Repasaremos algunos concepos básicos de la eoría maricial Nos cenraremos en aspecos relacionados con el álgebra lineal, la inversión y la diagonalización de marices Veremos algunas
En esta sección inicial el estudiante se va a familiarizar con el uso de algunos instrumentos de laboratorio.
 Prácica de Laboraorio Nº 1. INSTRUMENTOS DE LORTORIO EL INVERSOR LÓGIO. Objeivos : - Familiarizarse con el uso de algunos insrumenos de laboraorio. - Funcionamieno del inversor lógico. Medición de algunos
Prácica de Laboraorio Nº 1. INSTRUMENTOS DE LORTORIO EL INVERSOR LÓGIO. Objeivos : - Familiarizarse con el uso de algunos insrumenos de laboraorio. - Funcionamieno del inversor lógico. Medición de algunos
Tema 8: SERIES TEMPORALES
 Inroducción a la Economería Tema 8: ERIE TEMPORALE Tema 8: ERIE TEMPORALE. Concepo y componenes de una serie emporal. Definiremos una serie emporal como cualquier conjuno de N observaciones cuaniaivas
Inroducción a la Economería Tema 8: ERIE TEMPORALE Tema 8: ERIE TEMPORALE. Concepo y componenes de una serie emporal. Definiremos una serie emporal como cualquier conjuno de N observaciones cuaniaivas
Soluciones Acotadas para Ecuaciones Diferenciales Ordinarias de Orden 2
 Divulgaciones Maemáicas Vol. 7 No. 1 (1999), pp. 49 57 Soluciones Acoadas para Ecuaciones Diferenciales Ordinarias de Orden 2 Bounded Soluions for Second Order Ordinary Differenial Equaions Raúl Naulin
Divulgaciones Maemáicas Vol. 7 No. 1 (1999), pp. 49 57 Soluciones Acoadas para Ecuaciones Diferenciales Ordinarias de Orden 2 Bounded Soluions for Second Order Ordinary Differenial Equaions Raúl Naulin
Medición del tiempo de alza y de estabilización.
 PRÁCTICA # 2 FORMAS DE ONDA 1. Finalidad Esudiar la respuesa de configuraciones circuiales simples a diferenes formas de exciación. Medición del iempo de alza y de esabilización. Medición del reardo. Medición
PRÁCTICA # 2 FORMAS DE ONDA 1. Finalidad Esudiar la respuesa de configuraciones circuiales simples a diferenes formas de exciación. Medición del iempo de alza y de esabilización. Medición del reardo. Medición
LA VELOCIDAD DE CIRCULACION DE DINERO EN EL ECUADOR
 1 LA VELOCIDAD DE CIRCULACION DE DINERO EN EL ECUADOR José Luis Moncayo Carrera 1 Ec. Manuel González 2 RESUMEN El presene documeno iene como objeivo, presenar la aplicación de écnicas economéricas en
1 LA VELOCIDAD DE CIRCULACION DE DINERO EN EL ECUADOR José Luis Moncayo Carrera 1 Ec. Manuel González 2 RESUMEN El presene documeno iene como objeivo, presenar la aplicación de écnicas economéricas en
CORRELACIÓN LINEAL Y ANÁLISIS DE REGRESIÓN
 CORRELACIÓN LINEAL Y ANÁLISIS DE REGRESIÓN Auores: Alicia Vila (avilag@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Ana López (alopezra@uoc.edu), Ángel A. Juan (ajuanp@uoc.edu), MAPA CONCEPTUAL Definición
CORRELACIÓN LINEAL Y ANÁLISIS DE REGRESIÓN Auores: Alicia Vila (avilag@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Ana López (alopezra@uoc.edu), Ángel A. Juan (ajuanp@uoc.edu), MAPA CONCEPTUAL Definición
Indicadores demográficos METODOLOGÍA
 Indicadores demográicos METOOLOGÍA 1. Objeivos y uilidades El objeivo de esa operación esadísica es la obención de una serie de indicadores descripivos de la siuación demográica de Galicia, con la que
Indicadores demográicos METOOLOGÍA 1. Objeivos y uilidades El objeivo de esa operación esadísica es la obención de una serie de indicadores descripivos de la siuación demográica de Galicia, con la que
Uso de Análisis Factorial Dinámico para Proyecciones Macroeconómicas
 Uso de Análisis Facorial Dinámico para Proyecciones Macroeconómicas Alvaro Aguirre y Luis Felipe Céspedes * Resumen En ese rabajo implemenamos el méodo desarrollado por Sock y Wason (998) de análisis facorial
Uso de Análisis Facorial Dinámico para Proyecciones Macroeconómicas Alvaro Aguirre y Luis Felipe Céspedes * Resumen En ese rabajo implemenamos el méodo desarrollado por Sock y Wason (998) de análisis facorial
Macroeconomía II (2009) Universitat Autònoma de Barcelona Prof. Stefano Trento
 Macroeconomía II (009) Universia Auònoma de Barcelona Prof. Sefano Treno Problemas del Tema 1: Microfundamenos reales. Los problemas más imporanes esán marcados con una esrellia (*). Los oros son problemas
Macroeconomía II (009) Universia Auònoma de Barcelona Prof. Sefano Treno Problemas del Tema 1: Microfundamenos reales. Los problemas más imporanes esán marcados con una esrellia (*). Los oros son problemas
CARLOS FORNER RODRÍGUEZ Departamento de Economía Financiera y Contabilidad, UNIVERSIDAD DE ALICANTE
 ApunA es de Ingeniería Financiera TEMA 9: Value a Risk (VAR) CARLOS FORNER RODRÍGUEZ Deparameno de Economía Financiera y Conabilidad, UNIVERSIDAD DE ALICANTE En ese ema vamos a esudiar una forma alernaiva
ApunA es de Ingeniería Financiera TEMA 9: Value a Risk (VAR) CARLOS FORNER RODRÍGUEZ Deparameno de Economía Financiera y Conabilidad, UNIVERSIDAD DE ALICANTE En ese ema vamos a esudiar una forma alernaiva
Índice de Precios y Cotizaciones de la Bolsa Mexicana de Valores S.A.B. de C.V. (en adelante IPC y BMV respectivamente).
 Auorización SHCP: 09/11/2010 Fecha de publicación úlima modificación: 29/08/2014 Fecha de enrada en vigor: 05/09/2014 Condiciones Generales de Conraación del Conrao de Fuuro sobre el Índice de Precios
Auorización SHCP: 09/11/2010 Fecha de publicación úlima modificación: 29/08/2014 Fecha de enrada en vigor: 05/09/2014 Condiciones Generales de Conraación del Conrao de Fuuro sobre el Índice de Precios
FÍSICA. PRUEBA ACCESO A UNIVERSIDAD +25 TEMA 8. Corriente eléctrica
 FÍSC. PUEB CCESO UNESDD +5 TEM 8. Corriene elécrica Una corriene elécrica es el desplazamieno de las cargas elécricas. La eoría aómica acual supone ue la carga elécrica posiiva esá asociada a los proones
FÍSC. PUEB CCESO UNESDD +5 TEM 8. Corriene elécrica Una corriene elécrica es el desplazamieno de las cargas elécricas. La eoría aómica acual supone ue la carga elécrica posiiva esá asociada a los proones
Observatorio * EL AUMENTO DEL IVA EN ESPAÑA: UNA CUANTIFICACIÓN ANTICIPADA DE SUS EFECTOS **
 Revisa de Economía Aplicada E Número 53 (vol. XVIII), 2010, págs. 163 a 183 A Observaorio * EL AUMENTO DEL IVA EN ESPAÑA: UNA CUANTIFICACIÓN ANTICIPADA DE SUS EFECTOS ** GONZALO FERNÁNDEZ-DE-CÓRDOBA Universidad
Revisa de Economía Aplicada E Número 53 (vol. XVIII), 2010, págs. 163 a 183 A Observaorio * EL AUMENTO DEL IVA EN ESPAÑA: UNA CUANTIFICACIÓN ANTICIPADA DE SUS EFECTOS ** GONZALO FERNÁNDEZ-DE-CÓRDOBA Universidad
REVISTA INVESTIGACION OPERACIONAL Vol. 24, No. 1, 2003
 REVISTA INVESTIGACION OPERACIONAL Vol. 24, No. 1, 2003 ADAPTACION DE LOS TIPOS DE INTERES DE INTERVENCION A LA REGLA DE TAYLOR. UN ANALISIS ECONOMETRICO Carlos Paeiro Rodríguez 1, Deparameno de Análisis
REVISTA INVESTIGACION OPERACIONAL Vol. 24, No. 1, 2003 ADAPTACION DE LOS TIPOS DE INTERES DE INTERVENCION A LA REGLA DE TAYLOR. UN ANALISIS ECONOMETRICO Carlos Paeiro Rodríguez 1, Deparameno de Análisis
Condiciones Generales de Contratación de los Contratos de Futuro sobre Acciones (Liquidación en Especie)
 Condiciones Generales de Conraación de los Conraos de Fuuro sobre Acciones (Liquidación en Especie) I. OBJETO. 1. Acivo Subyacene. Las Acciones, Cerificados de Paricipación Ordinarios emiidos sobre Acciones
Condiciones Generales de Conraación de los Conraos de Fuuro sobre Acciones (Liquidación en Especie) I. OBJETO. 1. Acivo Subyacene. Las Acciones, Cerificados de Paricipación Ordinarios emiidos sobre Acciones
Construcción de señales usando escalones y rampas
 Consrucción de señales usando escalones y rampas J. I. Huircán Universidad de La Fronera March 3, 24 bsrac Se planean méodos para componer y descomponer señales basadas en escalones y rampas. Se de ne
Consrucción de señales usando escalones y rampas J. I. Huircán Universidad de La Fronera March 3, 24 bsrac Se planean méodos para componer y descomponer señales basadas en escalones y rampas. Se de ne
PRÁCTICA 4 TEMA 6: SERIES TEMPORALES
 PRÁCTICA 4 TEMA 6: SERIES TEMPORALES En las prácicas aneriores se habían analizado observaciones de variables de ipo ransversal (por ejemplo, obenidas para diferenes municipios). Llamaremos Serie Temporal
PRÁCTICA 4 TEMA 6: SERIES TEMPORALES En las prácicas aneriores se habían analizado observaciones de variables de ipo ransversal (por ejemplo, obenidas para diferenes municipios). Llamaremos Serie Temporal
DERECHOS BÁSICOS DE APRENDIZAJE matemáticas - grado 9
 4 Reconoce el significado de los eponenes racionales posiivos negaivos uiliza las lees de los eponenes. Por ejemplo: 7 7 7 + 7 4 7 7 7 7 40 ( 7 / ) / 7 / / 7 /0 0 7,... Uiliza la noación cienífica para
4 Reconoce el significado de los eponenes racionales posiivos negaivos uiliza las lees de los eponenes. Por ejemplo: 7 7 7 + 7 4 7 7 7 7 40 ( 7 / ) / 7 / / 7 /0 0 7,... Uiliza la noación cienífica para
01 Ejercicios de Selectividad Matrices y Sistemas de Ecuaciones
 01 Ejercicios de Selecividad Marices y Sisemas de Ecuaciones Ejercicios propuesos en 009 1- [009-1-A-1] a) [1 5] En un comercio de bricolaje se venden lisones de madera de res longiudes: 090 m, 150 m y
01 Ejercicios de Selecividad Marices y Sisemas de Ecuaciones Ejercicios propuesos en 009 1- [009-1-A-1] a) [1 5] En un comercio de bricolaje se venden lisones de madera de res longiudes: 090 m, 150 m y
Molécula de Azúcar ( C 12 H 22 O 11 ) Informe estadístico del sector agroindustrial de la caña de azúcar Zafras 2007/08 2013/14
 Molécula de Azúcar ( C 12 H 22 O 11 ) Informe esadísico del secor agroindusrial de la caña de azúcar Zafras 2007/08 2013/14 INTRODUCCIÓN Ese primer informe esadísico del secor agroindusrial de la caña
Molécula de Azúcar ( C 12 H 22 O 11 ) Informe esadísico del secor agroindusrial de la caña de azúcar Zafras 2007/08 2013/14 INTRODUCCIÓN Ese primer informe esadísico del secor agroindusrial de la caña
