d AB =r A +r B = 2GM
|
|
|
- Francisco José Macías Espejo
- hace 8 años
- Vistas:
Transcripción
1 Física de º Bachilleato Campo gavitatoio Actividad 1 [a] Enuncia la tecea ley de Keple y compueba su validez paa una óbita cicula. [b] Un satélite atificial descibe una óbita elíptica alededo de la Tiea, como se indica en la figua. Las velocidades en los extemos del eje mayo son v A y v B. Si la masa de la Tiea es M y la constante de la gavitación G, calcula la distancia AB. [c] Explica azonadamente si v A es mayo, igual o meno que v B. Tiea A B [a] Compueba que a pati de la tecea ley de Keple se puede deduci la ley de gavitación univesal. [b] En pime luga, se dibuja las velocidades, elativas al satélite, en los puntos A y B. vb A A Tiea B B v A El movimiento del satélite está egido po dos leyes de consevación: la del momento angula y la de la enegía mecánica. En consecuencia, se cumple que: A mv A = B mv B A v A = B v B B 1 mv A GMm A = 1 mv B GMm De la 1ª ecuación se deduce que:, simplificando se llega a: B v A GM A =v B GM ; llevando este esultado a la ª ecuación, escita A = v B v A B en la foma v B v A =GM( 1 B 1 A ), queda: v B v A =GM( 1 B v A v B B ) ; v B v A =GM( v B v A, de donde se puede obtene el valo de B : v B B ) B = GM(v B v A ) v B v b v A = GM(v B v A ) v B (v B v A )(v B +v A ) = GM v B (v B +v A ). El valo de A es, entonces, A = GM v A (v B +v A ) d AB = A + B = GM. Po lo tanto, la distancia AB es:. [c] El satélite evoluciona sometido a la acción de una fueza cental; en consecuencia, el momento angula del satélite especto a la Tiea se conseva, esto es, A mv A = B mv B ; A v A = B v B ; como en el punto A el satélite se encuenta más ceca de la Tiea que en el punto B, la apidez en A es mayo que la apidez en B. v A v B fagm, septiembe 009 { 1 }
2 Física de º Bachilleato Campo gavitatoio Actividad En los Juegos Olímpicos del año teeste 14 celebados en Mate, un atleta maciano obtiene la medalla de oo en salto de altua al supea el listón colocado a 5,75 m. [a] Calcula la gavedad en Mate. [b] Si las puebas olímpicas se hubiean ealizado en la Tiea, calcula la altua que hubiea podido salta el atleta maciano. DATOS: Constante de la Gavitación Univesal, G = 6, U.S.I., masa de Mate, M = 6, kg, adio de Mate, R = 3400 km, gavedad en la supeficie de la Tiea, g = 9,81 m/s². [a] Hay que entende, en pime luga, que gavedad en Mate significa intensidad del campo gavitatoio en su supeficie. Po lo tanto, g Mate =G M Mate 11 6,50$103 =6,67$10 =3,75. (3,4$10 6 ) kg [b] Se puede calcula la apidez con que el atleta maciano inicia el salto. De ente las ecuaciones del MRUA la más significativa ahoa es: v²-v o ² = a y; al aplicala al salto en Mate queda: 0 v o =$( 3,75)$5,75; v o =43,1; v o =6,57( m s). Paa calcula la altua en la Tiea aplicamos la misma ecuación, con la difeencia de que ahoa la incógnita es el desplazamiento vetical: 0 43,1 =$( 9,81)$ y y ; = 43,1 19,6 =,0m. R Mate fagm, septiembe 009 { }
3 Física de º Bachilleato Campo gavitatoio Actividad 3 La N.A.S.A. coloca en óbita cicula un satélite atificial de 300 kg de masa, de foma que un obsevado teeste, convenientemente situado, podía velo inmóvil en el fimamento. Este tipo de satélite se denomina geoestacionaio o geosincónico y se utiliza pincipalmente en comunicaciones. [a] Calcula el adio de la óbita y su altua especto a la supeficie teeste. [b] Detemina la enegía mecánica del satélite en su óbita. DATOS: Constante de la Gavitación Univesal, G = 6, U.S.I., masa de la Tiea, M = 5, kg, adio de la Tiea, R = 6370 km. [a] De la infomación del enunciado se deduce que el peiodo del satélite es de 4 h. Si se aplica la ª ley de Newton al satélite, se puede escibi: G M Tm =m ; po oto lado, sabemos que = T ; de ambas, simplificando la masa del satélite, se llega a: G M T = 4 ; ; 3 T 3 = GM TT 4 = 3 GM TT 4 =. La altua especto a 3 6,67$10 11 $5,97$10 4 $(8,64$10 4 ) 4 =4,$10 6 m =4.00km la supeficie teeste es: h = R T =4,$10 6 6,37$10 6 =35,8$10 6 m =35.800km. Vemos que los esultados son independientes de la masa del satélite y que la altua a que se encuenta un satélite geoestacionaio es casi seis veces el adio teeste (35800/6370 = 5,6). [b] La enegía mecánica de un cuepo que descibe una óbita cicula se calcula mediante: E m = G M Tm ; así que E m = 6.67$10 115,97$104 $300 $4,$10 = 1.4$10 9 (J). 7 fagm, septiembe 009 { 3 }
4 Física de º Bachilleato Campo gavitatoio Actividad 4 [a] Explica el concepto de enegía potencial gavitatoia. Qué enegía potencial gavitatoia tiene una patícula de masa m situada a una distancia de ota de masa M? [b] La enegía potencial gavitatoia de una patícula de masa m en las poximidades de la supeficie de un planeta, po ejemplo la Tiea, puede expesase en la foma apoximada E p = mgh, donde h es la altua especto a un cieto nivel de efeencia. En qué cicunstancias es válida esta expesión? El mencionado nivel de efeencia, debe se necesaiamente la supeficie del planeta? Razona tus contestaciones. [a] Consulta los apuntes de Física. [b] Si se toma como efeencia la supeficie del planeta, la enegía potencia gavitatoia de una patícula de masa m a una distancia del cento del planeta, de adio R, se calcula mediante: GMm U() = R = GMm[ 1 ]. Se cumple que, R =GMm[ 1 R 1 ]=GMm( R) R =R +h siendo h la altua de la patícula especto a la supeficie. En las poximidades del planeta, se puede hace la siguiente apoximación: =R +hjr, po lo que la expesión anteio se puede escibi como sigue: U =GMm h = GMmh, ya que. (R+h)R R =mg o h g o = GM R La condición que hemos impuesto es que la patícula se mueva ceca de la supeficie teeste; po oto lado, al hace la integal se ha supuesto que la enegía potencial gavitatoia es ceo en la supeficie del planeta. fagm, septiembe 009 { 4 }
5 Física de º Bachilleato Campo gavitatoio Actividad 5 [a] Escibe y comenta la Ley de Gavitación Univesal. [b] La Tiea tada un año en ealiza su óbita en tono al Sol. Esta óbita es apoximadamente cicula con adio R = 1, m. Sabiendo que G = 6, Nm²kg -, calcula la masa del Sol. [a] Consulta el libo de Física. [b] La Tiea evoluciona po la acción de la fueza de atacción gavitatoia del Sol; esta fueza se compota como fueza centípeta, po lo que, al aplica la ª ley de Newton al movimiento de la Tiea, queda: G M SM T =M ; la masa de la Tiea se puede simplifica T en esta expesión y, como = T, finalmente se llega a M S = 4 3. El peiodo del movimiento de la Tiea alededo del Sol vale: T =365(d as)$4 hoas s d a $3600 d a =3,15$10 7 (s). La masa del Sol es, entonces, 4 M S = $(1,49$10 11 ) 3 6,67$ $(3,15$10 7 ) =1,97$10 30 (kg) GT fagm, septiembe 009 { 5 }
6 Física de º Bachilleato Campo gavitatoio Actividad 6 Imagina un planeta sin atmósfea, pefectamente esféico, de adio R = 5000 km y masa M = kg. Desde su supeficie, se dispaa hoizontalmente un poyectil. G = 6, Nm²kg -. [a] Calcula la velocidad con que debe dispaase el poyectil paa que desciba una óbita cicula asante a la supeficie del planeta. [b] Explica qué es la velocidad de escape y calcúlala en nuesto caso. [a] Se aplica la ª ley de Newton al poyectil en su óbita cicula asante. El adio de esta óbita coincide con el adio del planeta, R. Se cumple que G Mm R =m v ; al simplifica, queda: R GM 6,67$10 11 $5$10 4 G M R =v ; v = R = 5$10 =8,17$10 3 ( m. 6 s ) m v M R $6,67$10 11 $5$10 4 [b] La velocidad de escape es la velocidad que hay que comunica a una patícula en la supeficie de un planeta paa que escape de su atacción gavitatoia. Se calcula mediante la expe- GM sión: v escape = R = 5$10 =1,15$10 4 ( m s). 6 Este esultado es coheente con el del apatado anteio: hace falta más enegía cinética paa lanza, desde la supeficie del planeta, un satélite al infinito que paa ponelo en óbita. fagm, septiembe 009 { 6 }
7 Física de º Bachilleato Campo gavitatoio Actividad 7 [a] Momento angula de una patícula: definición; teoema de consevación. [b] Un satélite atificial, de masa m = 00 kg, descibe una óbita cicula de adio R = 6700 km en tono a la Tiea. Calcula su momento angula especto al cento de la Tiea. Es constante? Po qué? DATOS: G = 6, Nm²kg - ; M T = 5, kg. [a] Véase el libo de Física. [b] El módulo del momento angula del satélite especto al cento de la Tiea se calcula mediante: L =Rmv, donde v es la apidez del satélite en su óbita. Esta apidez se puede calcula a pati de la ª ley de Newton aplicada al movimiento cicula del satélite: G M Tm R =m v, de donde se deduce que. En R v = R = 6,7$10 =7,7$10 3 ( m s) 6 consecuencia, L =6,7$10 6 (m)$00(kg)$7,7$10 3 ( m s) =1,03$10 13 kg$m s. GM T 6,67$10 11 $5,98$10 4 fagm, septiembe 009 { 7 }
8 Física de º Bachilleato Campo gavitatoio Actividad 8 La Luna es apoximadamente esféica, con adio R = 1, m y masa M = 7,3510 kg. [a] Calcula la aceleación de la gavedad en la supeficie luna. [b] Si se deja cae una pieda desde una altua de m sobe la supeficie luna, cuál seá su velocidad al choca con la supeficie? DATOS: G = 6, Nm²kg -. [a] La aceleación debida a la gavedad coincide numéicamente con la intensidad del campo gavitatoio, esto es, g o = GM R = 6,67$10 11 $7,35$10. (1,74$10 6 ) =1,6( kg ) [b] Se tata de un movimiento ectilíneo unifomemente aceleado; paa este ejecicio se puede utiliza la expesión: v v o =g o h; como la velocidad inicial es nula, v = $1,6$ =!,55( m s). En este caso, si consideamos positivas las magnitudes que apuntan hacia aiba, lo el signo - tiene sentido, así que la velocidad es -,55 (m/s). fagm, septiembe 009 { 8 }
9 Física de º Bachilleato Campo gavitatoio Actividad 9 [a] Enuncia la tecea ley de Keple y compueba que se cumple paa óbitas ciculaes en tono a un planeta esféico de masa M. [b] Los satélites de comunicaciones geoestacionaios desciben óbitas ciculaes en el plano ecuatoial de la Tiea. El peiodo de estas óbitas coincide con el de otación de la Tiea (un día), de foma que cada satélite geoestacionaio se encuenta siempe sobe el mismo punto del ecuado. Calcula el adio de esta óbita. DATOS: G = 6, Nm²kg - ; M T = 5, kg. [a] Se tata de deduci la 3ª ley de Keple a pati de la ley de la gavitación univesal y de las leyes de Newton de la dinámica. La fueza gavitatoia sobe un objeto en óbita cicula alededo de un planeta se compota como fueza centípeta, po lo que G Mm =m v, de donde se deduce que v = GM. Po oto lado, el peiodo del movimiento cicula del objeto es: T = v, po lo que T = 4 v ; al sustitui en esta igualdad el valo de la apidez antes calculado, se llega a: T = 4, expesión que coesponde a la 3ª ley de Keple. GM 3 [b] De la infomación del enunciado se deduce que el peiodo del satélite es de 4 h. Acabamos de ve que T = 4, de donde se deduce que 3 = GMT ; GM 3 = 3 GMT 4 = 3 6,67$10 11 $5,97$10 4 $(8,64$10 4 ) 4 4. =4,$10 6 m =4.00km fagm, septiembe 009 { 9 }
10 Física de º Bachilleato Campo gavitatoio Actividad 10 Una nave espacial, con los motoes apagados, descibe una óbita cicula de adio R =, m en tono a la Tiea. [a] Calcula la velocidad obital de la nave y el peiodo de la óbita. [b] Calcula la enegía cinética y la enegía potencial gavitatoia de la nave, de masa m = 510³ kg. [c] Cuánto tabajo tendían que ealiza, como mínimo, los motoes de la nave paa escapa de la atacción gavitatoia de la Tiea? Explica tu planteamiento. DATOS: G = 6, Nm²kg - ; M T = 5, kg. [a] Se aplica la ª ley de Newton a la nave espacial en su óbita cicula. La fueza gavitatoia sobe la nave espacial se compota como fueza centípeta, po lo que G M Tm =m v, de GM T 6,67$10 11 $5,98$10 4 donde se deduce que v = GM T ; v = =,55$10 =3,95$10 3 ( m s). El peiodo 7 es el tiempo invetido po la nave en una vuelta completa: T = v = $,55$107 3,95$10 =4,06$10 4 (s) =11,3(h). 3 [b] La enegía cinética es: E c = 1 mv = 1 5$103 $ (3,95$10 3 ) =3,90$10 10 (J). La enegía potencial gavitatoia vale: U = G M Tm = 6,67$10 11 $5,98$10 4 $5$10 3,55$10 = 7,8$10 10 (J) 7 [c] La enegía mecánica de la nave es: E m =3,90$10 10 (J) 7,8$10 10 (J) = 3,9$10 10 (J). Si se quiee que la nave escape de la atacción teeste, es deci, que llegue al infinito, debeá tene una enegía mecánica nula (sin enegía cinética ni potencial gavitatoia). En consecuencia, se debeá cumpli: E m,óbita +W motoes =E m, ; 3,9$10 10 (J) +W motoes =0; W motoes =3,9$10 10 (J). Este es el valo mínimo, ya que la nave llega al infinito con velocidad nula. fagm, septiembe 009 { 10 }
11 Física de º Bachilleato Campo gavitatoio Actividad 11 Tes patículas iguales de masa M están fijas en tes vétices de un cuadado de lado L. [a] Detemina el potencial gavitatoio en los puntos A y B, vétice vacante y cento del cuadado, espectivamente. [b] Si situamos una cuata patícula en el punto A y la soltamos con velocidad inicial nula, se moveá hacia B. Po qué? Detemina la velocidad de esta patícula cuando pase po B. Supón conocida la constante de gavitación univesal, G. M L B A M L M [a] El potencial gavitatoio del campo ceado po una patícula de masa M, a una distancia, se calcula mediante: V = G M. El potencial gavitatoio en el punto A es la suma de los potenciales gavitatoios asociados a las tes patículas; el punto A está de dos ellas a una distancia L, mientas que de la ota se encuenta a una distancia igual a la diagonal del cuadado: L. Po lo tanto, V total,a = G M L G M = 4GM L L GM L = GM(4+ ) L De manea simila se calcula el potencial gavitatoio en el punto B; en este caso, el punto se encuenta a la misma distancia de las tes patículas: L = L V total,b = 3 GM L = 3 GM L = 6 GM L ; en consecuencia, [b] Puede compobase que el potencia gavitatoio en A es mayo que el potencial gavitatoio en B; una patícula se mueve espontáneamente de los puntos de mayo potencial a los de meno potencial; po lo tanto, la cuata patícula se moveá de A a B. La simetía de la distibución sugiee que la cuata patícula se moveá según la diagonal que pasa po los puntos A y B. Paa detemina su velocidad en B tenemos en cuenta la consevación de la enegía mecánica: E m,a =E m,b ; mv A = 1 mv B +mv B ; al simplifica la masa de la cuata patícula, queda: V A V B = 1 v B ; v B =(V A V B ). Al sustitui los valoes de los potenciales gavitatoios se llega a: v B = GM(4+ ) L + 6 GM L = GM L ( 4 +6 ) =3,071 GM L 3GM L la patícula cuando pasa po B es, finalmente, v B =.. La velocidad de fagm, septiembe 009 { 11 }
12 Física de º Bachilleato Campo gavitatoio Actividad 1 [a] Escibe y comenta la Ley de Gavitación Univesal. [b] Calcula el adio de la óbita de Neptuno en tono al Sol, supuesta cicula, sabiendo que tada 165 años teestes en ecoela. DATOS: G = 6, Nm²kg - ; M Sol = 1, kg. [a] Véase cualquie libo de texto. [b] Si se aplica la ª ley de Newton al planeta Neptuno, se puede escibi: G M SM =M ; po oto lado, sabemos que = T ; de ambas, simplificando la masa del planeta, se llega a: G M S = 4 ; ; po oto lado, el peiodo del movimiento cicula de Neptuno vale: 3 T 3 = GM ST 4 T =165(años)$365 d as año $4 hoas d a $3600 s d a =5,0$10 9 (s); el adio de la óbita es, entonces, = GM ST 3 =4,50$10 1 m. 4 = 3 6,67$10 11 $1,99$10 30 $(5,$10 9 ) 4 fagm, septiembe 009 { 1 }
13 Física de º Bachilleato Campo gavitatoio Actividad 13 [a] La intensidad media del campo gavitatoio teeste en la supeficie de la Tiea es g = 9,81 N/kg. Calcula la masa de la Tiea. [b] A qué altua sobe la supeficie se educe g a la mitad del valo indicado? DATOS: G = 6, Nm²kg - ; adio de la Tiea: R = 6, m. [a] En la supeficie teeste, la intensidad del campo gavitatoio vale: g o =G M T R ecuación se deduce que M T = gor G = 9,81( /kg)$(6,37$106 ) (m ) 6,67$ ( m kg ) =5,98$10 4 (kg) ; de esta [b] Se ha de cumpli que g = 1 g o, es deci, G M T = 1, de donde se deduce que ; GM T R =R = R. Po oto lado, sabemos que =R +h, po lo que h = R; al sustitui el valo calculado de, queda: h = R R =( 1)R =0,414$6,37$10 6 =,64$10 6 (m). fagm, septiembe 009 { 13 }
14 Física de º Bachilleato Campo gavitatoio Actividad 14 Una sonda de exploación, de masa m = 500 kg, descibe una óbita cicula en tono a Mate. Sabiendo que el adio de dicha óbita es R = 3, m, que la masa de Mate es M = 6,410 3 kg y que G = 6, Nm²kg -, calcula: [a] La velocidad obital de la sonda y su momento angula especto al cento de Mate. [b] Las enegías cinética, potencial y mecánica de la sonda. [a] Se aplica la ª ley de Newton a la sonda de exploación en su óbita cicula. La fueza gavitatoia sobe la sonda se compota como fueza centípeta, po lo que G Mm =m v, de donde se deduce que v = GM GM 6,67$10 ; v = = 11 $6,4$10 3 3,50$10 =3,50$10 3 ( m s). 6 El módulo del momento angula de la sonda es: L =mv =3,50$10 6 (m)$500(kg)$3,50$10 3 ( m s) =6,13$10 1 kg$m s. [b] La enegía cinética es: E c = 1 mv = 1 5$10 $ (3,50$10 3 ) =3,06$10 9 (J). La enegía potencial gavitatoia vale: U = G Mm = 6,67$10 11 $6,4$10 3 $5$10 3,50$10 = 6,1$10 9 (J). 6 La enegía mecánica de la sonda es, entonces: E m =3,06$10 9 (J) 6,1$10 9 (J) = 3,06$10 9 (J). fagm, septiembe 009 { 14 }
15 Física de º Bachilleato Campo gavitatoio Actividad 15 [a] Explica los conceptos de enegía potencial gavitatoia y potencial gavitatoio. Qué potencial gavitatoio cea una patícula de masa M? Cómo son las supeficies equipotenciales? [b] Imagina dos esfeas iguales de masa M y adio R. Se sitúan de foma que la distancia ente sus centos es 10R y se libea una de ellas con velocidad inicial nula. Con qué velocidad se moveá cuando llegue a choca con la ota? Supón conocida la constante de gavitación univesal. 10R M M R R [a] Véase dichos conceptos en cualquie manual de Física. El potencial gavitatoio ceado po una patícula de masa M, en un punto situado a una distancia de su cento, está dado po: V = G M. Las supeficies equipotenciales son los lugaes geométicos en los que el potencial gavitatoio es constante; de acuedo con la expesión anteio, si V es constante, también lo es, po lo que el luga geomético de los puntos que equidistan de oto fijo es una cicunfeencia, si se tabaja en el plano, o una supeficie esféica, paa casos tidimensionales. [b] Las esfeas evolucionan sometidas a la acción de un campo consevativo, así que la enegía mecánica del sistema pemanece constante. Sea el estado 1 el mostado en el enunciado y sea el estado el epesentado a continuación: v 10R Tenemos que: E m,estado1 =E m,estado. En el estado 1 el sistema sólo tiene enegía potencial gavitatoia, mientas que en el estado el sistema tiene enegía cinética y enegía potencial gavitatoia; po lo tanto, G M 10R = 1 Mv G M 1 R ; Mv =G M R G M 1 10R ; Mv =G M 5R ; al dividi todo po M y multiplica po dos, queda: v = 4GM. La apidez de la esfea móvil 4GM 5R cuando choca con la esfea fija es, entonces, v =. 5R fagm, septiembe 009 { 15 }
16 Física de º Bachilleato Campo gavitatoio Actividad 16 [a] Explica el concepto de enegía potencial gavitatoia. Qué enegía potencial gavitatoia tiene una patícula de masa m situada a una distancia de ota de masa M? [b] Seguo que la expesión E p = mgh paa la enegía potencial gavitatoia te esulta familia. Explica su significado y las cicunstancias en las que es aplicable. [a] Consulta el libo, o incluso los apuntes, de Física. La enegía potencial gavitatoia de una patícula de masa m, en un punto situado a una distancia de ota patícula de masa M, está dada po: U = G Mm. [b] Si se toma como efeencia la supeficie del planeta, la enegía potencia gavitatoia de una patícula de masa m a una distancia del cento del planeta, de adio R, se calcula mediante: GMm U() = R = GMm[ 1 ]. Se cumple que, R =GMm[ 1 R 1 ]=GMm( R) R =R +h siendo h la altua de la patícula especto a la supeficie. En las poximidades del planeta, se puede hace la siguiente apoximación: =R +hjr, po lo que la expesión anteio se puede escibi como sigue: U =GMm h = GMmh, ya que. (R+h)R R =mg o h g o = GM R La condición que hemos impuesto es que la patícula se mueva ceca de la supeficie teeste; po oto lado, al hace la integal se ha supuesto que la enegía potencial gavitatoia es ceo en la supeficie del planeta. fagm, septiembe 009 { 16 }
17 Física de º Bachilleato Campo gavitatoio Actividad 17 [a] Momento angula de una patícula: definición; teoema de consevación. [b] Un cometa ealiza una óbita elíptica con el Sol en uno de los focos. El cociente ente las a distancias máxima (afelio) y mínima (peihelio) del cometa al cento del Sol es. Calcula la elación ente las velocidades del cometa en estos dos puntos,. v a v p p =100 [a] Véase el libo de Física. [b] En pime luga, dibujamos un esquema con las posiciones del cometa especto al Sol: P Sol p a v p va A El cometa evoluciona sometido a la acción de una fueza cental; en consecuencia, el momento angula del cometa especto al Sol se conseva, esto es, a mv a = p mv p ; de donde a se deduce que: p = vp v a v a ; estos cocientes son iguales a 100, po lo que v p =0,01; como en el punto P el cometa se encuenta más ceca del Sol que en el punto A, la apidez en P es mayo que la apidez en A. La distancia al Sol y la apidez del cometa son invesamente popocionales. fagm, septiembe 009 { 17 }
18 Física de º Bachilleato Campo gavitatoio Actividad 18 [a] Enuncia las Leyes de Keple. [b] Euopa es un satélite de Júpite que tada 3,55 días en ecoe su óbita, de 6, m de adio medio, en tono a dicho planeta. Oto satélite de Júpite, Ganímedes, tiene un peiodo obital de 7,15 días. Calcula el adio medio de la óbita de Ganímedes y la masa de Júpite. Constante de gavitación: G = 6, Nm²kg -. [a] Consulta el libo de Física. [b] En pime luga, se dibuja un esquema con los dos satélites de Júpite. Se ha de cumpli paa los mismos la 3ª ley de Keple: los cuadados de los peiodos son popocionales a los cubos de las distancias medias de los satélites al planeta, esto T es, T, que se puede escibi: T E = [ G ; G = E T G T E = 3 Euopa 3 Gan medes T G E ] 3 3 G =6,71$10 8 (m)$ G =1,07$10 9 (m). 7,15 d as 3,55 d as 3 Euopa E G Ganímedes Paa halla la masa de Júpite nos fijamos en los datos elativos al satélite Euopa. Éste evoluciona po la acción de la fueza de atacción gavitatoia de Júpite; esta fueza se compota como fueza centípeta, po lo que, al aplica la ª ley de Newton al movimiento de Euopa, queda: G M JM E =M ; la masa de Euopa se puede simplifica en esta expe- E sión y, como = T, finalmente se llega a M J = 4 3 GT. El peiodo del movimiento de Euopa alededo de Júpite vale: T =3,55(d as)$4 hoas s d a $3600 d a =3,07$10 5 (s). La masa de Júpite es, entonces, 4 M J = $(6,71$10 8 ) 3. 6,67$10 11 $(3,07$10 5 ) =1,90$10 7 (kg) fagm, septiembe 009 { 18 }
19 Física de º Bachilleato Campo gavitatoio Actividad 19 [a] Explica el concepto de campo gavitatoio ceado po una o vaias patículas. [b] Dos patículas de masas M 1 y M = 4M 1 están sepaadas una distancia d = 3 m. En el punto P, situado ente ellas, el campo gavitatoio total ceado po estas patículas es nulo. Calcula la distancia x ente P y M 1. M x P 1 d M i=n gi i=1 [a] Si se dispone en una egión del espacio de una o más patículas, el espacio alededo de las mismas adquiee cietas caacteísticas que no existían cuando las patículas no estaban. Este hecho se puede compoba acecando ota patícula de pueba. Decimos que las patículas oiginales han ceado un campo gavitatoio. Éste está descito vectoialmente mediante la llamada intensidad del campo gavitatoio. Si el campo gavitatoio está ceado po vaias patículas, la intensidad del campo gavitatoio esultante es la suma vectoial de las intensidades individuales: g total =. [b] Dibujamos los vectoes intensidad del campo gavitatoio, ceados po cada una de las patículas, en el punto P: M g P g 1 1 Los módulos de dichas intensidades son: g 1 =G M 1 x y g. Como la intensidad del =G 4M 1 (3 x) campo gavitatoio esultante es nula, se cumpliá que g total =g 1 g =0; G M 1 x =G 4M 1 ; (3 x) ; si se extae la aíz cuadada, tenemos: x = 3 x ; x = 3-x; 3x = 3; x = 1 (m). 1 x = 4 (3 x) x d M fagm, septiembe 009 { 19 }
20 Física de º Bachilleato Campo gavitatoio Actividad 0 [a] Escibe y comenta la Ley de Gavitación Univesal. [b] Recientemente ha sido puesto en óbita el satélite euopeo Envisat (envionment satellite; satélite del medio ambiente). La altua de su óbita sobe la supeficie de la Tiea es h = 800 km. Calcula la velocidad obital del Envisat y el peiodo de su óbita. DATOS: G = 6, Nm²kg - ; M T = 5, kg; R T = 6, m. [a] Véase el libo de Física. [b] El adio de la óbita del Envisat es: =R T +h =6,37$ ,8$10 6 =7,17$10 6 (m). Se aplica la ª ley de Newton a dicho satélite en su óbita cicula. La fueza gavitatoia sobe el mismo se compota como fueza centípeta, po lo que G M Tm =m v, de donde se deduce GM T 6,67$10 11 $5,97$10 4 que v = GM T ; v = = 7,17$10 =7,45$10 3 ( m s). El peiodo es el tiempo 6 invetido po la nave en una vuelta completa: T = v = $7,17$106 7,45$10 =6,05$10 3 (s) =1,68(h). 3 fagm, septiembe 009 { 0 }
21 Física de º Bachilleato Campo gavitatoio Actividad 1 [a] Calcula la intensidad del campo gavitatoio, g, en la supeficie de Júpite. A qué altua sobe la supeficie de Júpite, h, se educe g al valo supeficial teeste de 9,81 N/kg? DATOS: G = 6, Nm²kg - ; M J = 1, kg; R J = 6, m. [b] El peiodo de oscilación de un péndulo simple en la supeficie de la Tiea es T = 1, s. Cuál seía su peiodo de oscilación en la supeficie de Júpite? [a] En la supeficie de Júpite la intensidad del campo gavitatoio se calcula mediante: g o =G M J. Esta intensidad es algo más de dos veces y media R = 6,67$10 11 $1,90$10 7 =6,0 J (6,98$10 7 ) kg supeio a la existente en la supeficie teeste. A una distancia del cento de Júpite, la intensidad del campo gavitatoio es: g =G M J ; de GM J 6,67$10 11 $1,90$10 7 donde se deduce que = GM J g ; = g = 9,81 =1,14$10 8 (m); la altua sobe la supeficie seá, entonces, h = R J =1,14$10 8 6,98$10 7 =4,4$10 6 (m). [b] El peiodo de oscilación de un péndulo de longitud L está dado po la expesión: T = L g L g o,tiea En la supeficie teeste, el peiodo es: T Tiea =. L g o,júpite En la supeficie jupiteina, el peiodo vale: T Júpite =. T Júpite T Tiea = g o,tiea g o,júpite Al dividi la segunda ecuación po la pimea, se obtiene: ; T Júpite 9,81 T Tiea = 6 =0,614; T Júpite =0,614$T Tiea =0,614$1,(s) =0,737(s). Este esultado es coheente con el hecho de que, cuanto mayo sea la atacción gavitatoia, meno seá la duación de una oscilación completa del péndulo. fagm, septiembe 009 { 1 }
22 Física de º Bachilleato Campo gavitatoio Actividad [a] Explica el concepto de enegía potencial gavitatoia. Qué enegía potencial gavitatoia tiene una patícula de masa m situada a una distancia de ota patícula de masa M? [b] Un planeta esféico sin atmósfea tiene masa M = 1,10 3 kg y adio R = 1,310 6 m. Desde su supeficie se lanza veticalmente un poyectil que llega a alcanza una altua máxima h = R/ antes de volve a cae hacia la supeficie. Con qué velocidad inicial se ha lanzado el poyectil? G = 6, Nm²kg -. [a] Consulta el libo, o incluso los apuntes, de Física. La enegía potencial gavitatoia de una patícula de masa m, en un punto situado a una distancia de ota patícula de masa M, está dada po: U = G Mm. [b] Se tata de un ejecicio que puede esolve fácilmente mediante la ley de consevación de la enegía mecánica; peo antes, dibujamos un esquema de la situación. La posición final del poyectil es: =R +h =R + R = 3R. Se cumple que: v = 0 E m,inicial =E m,final R v o h=r/ 1 mv o G Mm R = GMm Al dividi todo po m vemos que el esultado es independiente de la masa del poyectil: 1 v o =GM( 1 R ) 3R v o =GM 1 3R ; v o = GM 3R v o = $6,67$10 11 $1,$10 3 3$1,3$10 =,03$10 3 ( m s). 6 fagm, septiembe 009 { }
23 Física de º Bachilleato Campo gavitatoio Actividad 3 Un satélite atificial descibe una óbita elíptica, con el cento de la Tiea en uno de sus focos. [a] En el movimiento obital del satélite, se conseva su enegía mecánica? Y su momento v angula especto al cento de la Tiea? Razona P tus espuestas. [b] Supón que se conocen las distancias máxima y mínima del satélite al cento de la Tiea (apogeo y peigeo), R A y R P espectivamente. Plantea azonadamente, sin esolvelas, las R P R A ecuaciones necesaias paa detemina las M velocidad obitales del satélite en estos puntos, v A y v P. DATOS: Constante de gavitación univesal, G. v A Masa de la Tiea, M. [a] Si se supone que el satélite evoluciona sometido exclusivamente a la acción del campo gavitatoio teeste, que es un campo consevativo, la enegía mecánica del satélite pemanece constante. La fueza gavitatoia sobe el satélite es una fueza cental, así que el momento de la misma especto al cento de la Tiea es nulo; en consecuencia, el momento angula del satélite también pemanece constante. [b] La consevación de la enegía mecánica exige que: E m,p =E m,a, esto es, 1 mv P G Mm R P = 1 mv A G Mm R A ; al dividi po la masa del satélite m, multiplica po dos y eodena los téminos de la igualdad, se llega a: v P v A =GM 1 (1) R P 1 R A La consevación del momento angula implica que: R P mv P =R A mv A ; R P v P =R A v A () Resolviendo el sistema fomado po las ecuaciones (1) y () se obtendía las velocidad obitalev A y v P. Si tienes ganas, puedes compoba que las soluciones de este sistema de ecuacio- nes son: v A = v P = GMR P R A (R A +R P ) GMR A R P (R A +R P ) fagm, septiembe 009 { 3 }
24 Física de º Bachilleato Campo gavitatoio Actividad 4 [a] Explica el concepto de campo gavitatoio ceado po una o vaias patículas. [b] La distancia ente los centos de la Tiea y la Luna es d = 3, m. En un cieto punto P, situado ente ambas, el campo gavitatoio total es nulo. Sabiendo que la masa de la Tiea es 81 veces supeio a la de la Luna, calcula la distancia x ente P y el cento de la Luna. Tiea d P x Luna [a] Véase la actividad 19. [b] Dibujamos los vectoes intensidad del campo gavitatoio, ceados po la Tiea y la Luna, en el punto P: Tiea g 1 g P x d Luna Los módulos de dichas intensidades son: g 1 =G M T y g =G M L. Como la intensidad del campo gavitatoio esultante es nula, se cumpliá que g total =g 1 g =0; G M L x =G M T ; ( d x x ) = M T M L ; si se extae la aíz cuadada, tenemos: M L ; el miembo de la deecha vale 9, po lo que d x =9x;d=10x;x= d 10 =3,84$107 (m). (d x) d x x = M T x (d x) fagm, septiembe 009 { 4 }
25 Física de º Bachilleato Campo gavitatoio Actividad 5 Dos planetas esféicos tienen masas difeentes, M 1 y M = 9M 1, peo en sus supeficies la intensidad del campo gavitatoio es la misma, g 1 = g. [a] Calcula la elación ente los adios de los planetas, R /R 1, y ente sus densidades de masa, / 1. [b] Son iguales las velocidades de escape desde las supeficies de los dos planetas? Razona tu espuesta. [a] En pime luga, escibimos las expesiones de las intensidades de campo gavitatoio g 1 =G M 1 R debidas a los dos planetas: 1. Si son iguales se cumpliá que ;. g =G 9M R R 1 =9R 1 R 1 =3 R En función de la densidad y del tamaño del planeta, la masa del mismo es: M 1 = 4 3 R Las intensidades de campo gavitatoio son, ahoa: g 1 = 4 3 G R 1 1. Si estas intensidades g = 4 3G R son iguales, se cumpliá: R 1 1 =R ;. 1 = R 1 R = 1 3 [b] La velocidad de escape es la velocidad que hay que comunica a una patícula en la supeficie de un planeta paa que escape de su atacción gavitatoia. Se calcula mediante la expesión: v escape = R = gr. Vemos que la velocidad de escape depende de la intensidad GM de campo gavitatoio en la supeficie del planeta y del adio del mismo. En nuesto caso, los dos planetas tienen el mismo valo de la intensidad y difeente adio (R > R 1 ); po lo tanto, la velocidad de escape seá mayo paa el segundo planeta. fagm, septiembe 009 { 5 }
26 Física de º Bachilleato Campo gavitatoio Actividad 6 [a] Enuncia las Leyes de Keple y demuesta la tecea en el caso paticula de óbita ciculaes. [b] Neptuno y la Tiea desciben óbitas en tono al Sol, siendo el adio medio de la pimea óbita teinta veces mayo que el de la segunda. Cuántos años teestes tada Neptuno en ecoe su óbita? [a] Consulta el libo de Física. Se tata de deduci la 3ª ley de Keple a pati de la ley de la gavitación univesal y de las leyes de Newton de la dinámica. La fueza gavitatoia sobe un objeto en óbita cicula alededo de un planeta se compota como fueza centípeta, po lo que G Mm =m v, de donde se deduce que v = GM. Po oto lado, el peiodo del movimiento cicula del objeto es: T = v, po lo que T = 4 v ; al sustitui en esta igualdad el valo de la apidez antes calculado, se llega a: T = 4, expesión que coesponde a la 3ª ley de Keple. GM 3 T = 3 eptuno [b] De acuedo con la 3ª ley de Keple, T ; ; T eptuno T Tiea = eptuno 3/ Tiea T eptuno = eptuno 3 Tiea T eptuno T Tiea = 3/ ; Tiea TTiea =30 3/ $1(año) =9,7(años). eptuno 3 Tiea fagm, septiembe 009 { 6 }
27 Física de º Bachilleato Campo gavitatoio Actividad 7 [a] Explica cómo es y qué intensidad tiene el campo gavitatoio en las poximidades de la supeficie teeste. Qué enegía potencial gavitatoia tiene una patícula de masa m en pesencia de este campo? Explica tu contestación. [b] Desde una altua especto al suelo h = 10 m se lanza una patícula con velocidad inicial v i = 0 m/s, fomando un vi ángulo α = 30º con la hoizontal. Supuesta despeciable la ficción con el aie, detemina la velocidad de la patícula cuando choca con el suelo, v f α (módulo, v f, y ángulo especto al suelo, θ). Considea g = 10 m/s². h v f θ [a] Véase cualquie libo de Física. [b] En pime luga, se elige un sistema de efeencia; las condiciones iniciales son, entonces, x o =0 v i,x =0 cos 30 =17,3( m s) a continuación, se esciben las ecuaciones de y o =10(m) v i,y =0sen30 =10,0( m s) los movimientos en los ejes X e Y: y EjeX x =17,3$t v a=-10 (m/s ) i v x =17,3( m s) vi,y α EjeY y =10 +10$t 5$t v i,x v y =10 10$t El tiempo que tada en llega al suelo x se obtiene de la condición: y = 0, 0 =10 +10$t 5$t ; t =,73(s) ; θ así que las componentes de la velocidad cuando la patícula llega al suelo vf v x =17,3( m s) son:. El v y =10 7,3 =17,3( m s) módulo de esta velocidad es: v = v x +v y =17,3$ =4,5( m s), la cual foma con la hoizontal un ángulo = 45 o. fagm, septiembe 009 { 7 }
28 Física de º Bachilleato Campo gavitatoio Actividad 8 L L [a] Momento angula de una patícula: definición; teoema de consevación. [b] Un satélite atificial de masa m = 500 kg descibe una óbita cicula en tono a la Tiea, a una altua h = 600 km sobe su supeficie. Calcula el módulo del momento angula del satélite especto al cento de la Tiea. Si la óbita está en el plano ecuatoial, qué diección tiene el momento angula,? Es un vecto constante? Po qué? DATOS: G = 6, Nm²kg -. Masa y adio de la Tiea: M T = 5, kg; R T = 6, m. [a] Consulta el libo de Física. [b] En pime luga, se calcula la velocidad del satélite en su óbita cicula. El adio de la óbita del satélite es: =R T +h =6,37$ ,6$10 6 =6,97$10 6 (m) La fueza gavitatoia sobe el mismo se compota como fueza centípeta, po lo que G M Tm =m v, de donde se GM T 6,67$10 11 $5,98$10 4 deduce que v = GM T ; v = = 6,97$10 =7,56$10 3 ( m s). 6 El módulo del momento angula se calcula mediante: L =mv =6,97$10 6 (m)$500(kg)$7,56$10 3 ( m s) =,63$10 13 kg$m s. La diección del momento angula es pependicula al plano de la óbita, esto es, pependicula al plano ecuatoial. Se tata de un vecto constante, ya que el momento angula del satélite especto al cento de la Tiea se conseva. La consevación del momento angula es debido a que el momento de la fueza gavitatoia sobe el satélite, especto al cento de la Tiea, es ceo. El sentido del momento angula se muesta en la siguiente figua. L v Satélite Tiea fagm, septiembe 009 { 8 }
29 Física de º Bachilleato Campo gavitatoio Actividad 9 [a] Escibe y comenta la Ley de Gavitación Univesal. [b] Se deja cae un cuepo desde una altua h = m sobe la supeficie de la Luna. Calcula su velocidad cuando choca con la supeficie y el tiempo de caída. DATOS: G = 6, Nm²kg -. Masa y adio de la Luna: M L = 7,3410 kg; R L = 1, m. [a] Consulta cualquie libo de Física. [b] Hemos se calcula la aceleación en la supeficie luna; esta aceleación coincide numéicamente con la intensidad del campo gavitatoio en la supeficie de la Luna, esto es, a L =g o =G M L 11 7,34$10 =6,67$10. Con el sistema de efeencia mostado R L (1,74$10 6 ) =1,6 m s en la figua, y teniendo en cuenta que se tata de un movimiento ectilíneo unifomemente aceleado, se puede escibi: vo = 0 m x a = 1,6 m/s² v v o =a y v = a y =! $1,6$ =,55( m s) De las dos soluciones que tiene la aíz cuadada, se ha elegido el signo +, que es el que tiene sentido de acuedo con el sistema de efeencia. v=? y fagm, septiembe 009 { 9 }
30 Física de º Bachilleato Campo gavitatoio Actividad 30 La aceleación de la gavedad en la supeficie de Mate es g = 3,87 m/s². [a] Calcula la masa de Mate. [b] Se lanza veticalmente un objeto desde la supeficie de Mate, con velocidad inicial igual a la mitad de la de escape. Calcula la máxima altua sobe la supeficie, h, que llega a alcanza el objeto. DATOS: G = 6, Nm²kg -. Radio de la Tiea: R M = 3,310 6 m. [a] La intensidad del campo gavitatoio en la supeficie de Mate es: deduce que: M M = gor M G = 3,87( /kg)$(3,3$106 ) (m ). 6,67$10 11 ( m /kg ) =6,40$10 3 (kg) [b] Se sabe que la velocidad de escape está dada po: v escape = GM M R M g o =G M M R M ; de donde se. El objeto se mueve en un campo de fuezas consevativo en el que la enegía mecánica pemanece constante. Po lo tanto; E m,inicial =E m,final h=? v = 0 RM v o = v / escape 1 mv o G M Mm R M = G M Mm Si se divide todo po la masa m del objeto y se sustituye la velocidad inicial po su valo, queda: 1 1 GM M R M GM M Simplificando se llega a: R M = GM M GM M R M = GM M = 4 3 R M; h = R M = 4 3 R M R M = 1 3 R M; h = 1 3 3,3$106 =1,11$10 6 (m). fagm, septiembe 009 { 30 }
31 Física de º Bachilleato Campo gavitatoio Actividad 31 Un satélite de masa m = 500 kg descibe una óbita cicula de adio = 7, m en tono a la Tiea. [a] Calcula la velocidad obital del satélite. [b] Paa pasa a ota óbita cicula de adio, cuánto tabajo deben ealiza los motoes del satélite? DATOS: G = 6, Nm²kg -. Masa de la Tiea: M T = 5, kg. [a] Se aplica la ª ley de Newton al satélite en su óbita cicula. La fueza gavitatoia sobe el satélite se compota como fueza centípeta, po lo que G M Tm =m v, de donde se deduce GM T 6,67$10 11 $5,98$10 4 que v = GM T ; v = = 7,50$10 =7,9$10 3 ( m s). 6 [b] El tabajo que tienen que hace los motoes es la difeencia ente las enegías mecánicas final e inicial: W motoes =E m,final E m,inicial. Po oto lado, la enegía mecánica de un objeto de masa m que descibe una óbita cicula de adio en tono a la Tiea está dada po: E m = GM Tm ; en consecuencia, W motoes = GM Tm 4 + GM Tm =GM T m( ) = GM Tm 4 W motoes = 6,67$10 11 $5,98$10 4 $500 4$7,50$10 6 =6,65$10 9 (J) fagm, septiembe 009 { 31 }
32 Física de º Bachilleato Campo gavitatoio Actividad 3 [a] Explica el concepto de campo gavitatoio ceado po una o vaias patículas. La Tiea es apoximadamente esféica, de adio R T = 6, m. La intensidad media del campo gavitatoio en su supeficie es g g = 9,81 m/s². [b] Calcula la densidad de masa media de la Tiea, ρ. [c] A qué altua h sobe la supeficie de la Tiea se educe g a la cuata pate de g o? DATO: G = 6, Nm²kg -. i=n gi i=1 [a] Si se dispone en una egión del espacio de una o más patículas, el espacio alededo de las mismas adquiee cietas caacteísticas que no existían cuando las patículas no estaban. Este hecho se puede compoba acecando ota patícula de pueba. Decimos que las patículas oiginales han ceado un campo gavitatoio. Éste está descito vectoialmente mediante la llamada intensidad del campo gavitatoio. Si el campo gavitatoio está ceado po vaias patículas, la intensidad del campo gavitatoio esultante es la suma vectoial de las intensidades individuales: g total =. [b] La densidad es la masa po unidad de volumen; paa el caso de la Tiea, la densidad está dada po: = M T. Vemos que se necesita conoce la masa de la Tiea. Esta V T = M T 4 = 3M T 3 R T 3 4 R3 T magnitud se puede calcula a pati de la intensidad del campo gavitatoio en la supeficie teeste: g o =G M T ; de donde se deduce que M T = gor T ; sustituyendo este valo en la expe- R T G 3$9,81 sión anteio tenemos: = 3goR T 3go 4 GR t = 4 $6,67$ $6,37$10 =5,51$10 3 kg 6 m 3 4 GR T 3 = [c] A una distancia del cento de la Tiea, la intensidad del campo gavitatoio es: g =G M T ; po oto lado, la intensidad del campo gavitatoio en la supeficie teeste es: g o =G M T ; al dividi la segunda po la pimea, queda: g o g = R T lo que =4R T ; =R T ; la altua sobe la supeficie es, entonces, h = R T =R T =6,37$10 6 (m). ; el miembo de la izquieda vale 4, po R T fagm, septiembe 009 { 3 }
33 Física de º Bachilleato Campo gavitatoio Actividad 33 [a] Calcula la velocidad de escape desde la supeficie de la Luna. [b] Se lanza veticalmente un objeto desde la supeficie de la Luna, con velocidad inicial igual a la de escape. A qué distancia del cento de la Luna se educe su velocidad a la mitad de la inicial? DATOS: G = 6, Nm²kg -. Masa y adio de la Luna: M L = 7,3410 kg; R L = 1, m. [a] La velocidad de escape es la velocidad que hay que comunica a una patícula en la supeficie luna paa que escape de su atacción gavitatoia. Se calcula mediante la aplicación de la ley de consevación de la enegía mecánica: E m,inicial =E m,, esto es, 1 mv escape G M Lm GM R L =0; de donde se deduce que v escape = L. [b] El objeto se mueve en un campo de fuezas consevativo en el que la enegía mecánica pemanece constante. Po lo tanto; E m,inicial =E m,final RL v = v escape / =? v o = v escape 1 mv escape R L G M Lm R L = 1 m1 4 v escape G M Lm De esta ecuación hemos de obtene el valo de ; antes de que el alumno se lance como un poseso a sustitui valoes, es conveniente lleva a cabo alguna simplificación algebaica. Si se divide todo po la masa m del objeto y se multiplica po ocho, queda: 4v escape 8G M L R L =v escape 8G M L 3v escape 8G M L R L = 8G M L Sustituyendo la velocidad de escape po su valo se llega a: 6G M L R L 8G M L R L = 8G M L ; G M L R L = 8G M L ; R L = 8 ; =4R L =4$1,74$10 6 =6,96$10 6 (m). Obseva la sencillez y la elegancia de la espuesta po habe utilizado leticas. fagm, septiembe 009 { 33 }
34 Física de º Bachilleato Campo gavitatoio Actividad 34 Desde la supeficie de un planeta esféico sin atmósfea, de adio R =,310 6 m y masa M = 8,610 3 kg, se dispaa un poyectil con velocidad inicial v o hoizontal, es deci, en diección tangente a la supeficie. [a] Calcula el valo de v o paa que el poyectil desciba una óbita cicula asante a la supeficie del planeta. Cuál es el peiodo de esta óbita? [b] Si el poyectil se dispaa con una velocidad doble de la anteio, escapaá de la atacción gavitatoia del planeta? Justifica tu espuesta. DATO: G = 6, Nm²kg -. [a] Se aplica la ª ley de Newton al poyectil en su óbita cicula asante. El adio de esta óbita coincide con el adio del planeta, R. Se cumple que GM 6,67$10 11 $8,6$10 3 G Mm R =m v o ; al simplifica, queda: R G M R =v o ; v o = R =,3$10 =5,00$10 3 ( m. El peiodo de esta óbita es: 6 s ) T = R v o = $,3$106 5$10 =,89$10 3 (s) =0,80(h). 3 m v o M R $6,67$10 11 $8,6$10 3 [b] La velocidad de escape es la velocidad que hay que comunica a una patícula en la supeficie de un planeta paa que escape de su atacción gavitatoia. Se calcula mediante la expe- GM sión: v escape = R =,3$10 =7,06$10 3 ( m s). 6 Si se lanza el poyectil con una velocidad doble de la obtenida en el apatado anteio, se supea con ceces la velocidad de escape y el poyectil escapa de la atacción gavitatoia del planeta; incluso llega al infinito con una velocidad distinta del ceo. fagm, septiembe 009 { 34 }
35 Física de º Bachilleato Campo gavitatoio Actividad 35 [a] Explica el concepto de enegía potencial gavitatoia. Qué enegía potencial gavitatoia tiene una patícula de masa m situada a una distancia de ota patícula de masa M? [b] Un meteoito se diige hacia la Luna, de masa M L = 7,3410 kg y adio R L = 1, m. A una altua h = 3R L sobe la supeficie de la Luna, la velocidad del meteoito es v o = 500 m/s. Calcula su velocidad cuando choca con la supeficie. DATO: G = 6, Nm²kg -. [a] Consulta el libo de Física. [b] La enegía mecánica del meteoito pemanece constante, ya que evoluciona en un campo consevativo. En el instante inicial el meteoito se encuenta a una distancia =h +R L =4R L del cento de la Luna. Se cumple, entonces, que: RL v =? v o h = 3R L E m,inicial =E m,final 1 mv o G M Lm 4R L = 1 mv G M Lm R L Si se multiplica toda po dos y se divide po la masa del meteoito m, se obtiene: v o G M L R L =v G M L R L v =v o +3G M L R L ; v = v o +3G M L R L v = $6,67$10 11 $7,34$10 $1,74$10 6 =1,68$10 3 ( m s) La velocidad del meteoito cuando choca con la supeficie luna es mayo, como tiene que se, que la que tenía inicialmente. fagm, septiembe 009 { 35 }
36 Física de º Bachilleato Campo gavitatoio Actividad 36 [a] Enuncia las Leyes de Keple y demuesta la tecea en el caso paticula de óbitas ciculaes. [b] Rhea y Titán son dos satélites de Satuno que tadan, espectivamente, 4,5 y 15,9 días teestes en ecoe sus óbitas en tono a dicho planeta. Sabiendo que el adio medio de la óbita de Rhea es 5,910 8 m, calcula el adio medio de la óbita de Titán y la masa de Satuno. DATO: G = 6, Nm²kg -. [a] Se tata de deduci la 3ª ley de Keple a pati de la ley de la gavitación univesal y de las leyes de Newton de la dinámica. La fueza gavitatoia sobe un objeto en óbita cicula alededo de un planeta se compota como fueza centípeta, po lo que G Mm =m v, de donde se deduce que v = GM. Po oto lado, el peiodo del movimiento cicula del objeto es: T = v, po lo que T = 4 v ; al sustitui en esta igualdad el valo de la apidez antes calculado, se llega a: T = 4, expesión que coesponde a la 3ª ley de Keple. GM 3 [b] En pime luga, se dibuja un esquema con los dos satélites de Satuno. Se ha de cumpli paa los mismos la 3ª ley de Keple: los cuadados de los peiodos son popocionales a los cubos de las distancias medias de los satélites al planeta, esto es, T, que se T R puede escibi: T T = [ R ; T = R T T T R 3 T =5,9$10 8 (m)$ T =1,$10 9 (m). T ] 3 15,9 d as 4,5 d as 3 Rhea T 3 Rhea = 3 Titán Titán Paa halla la masa de Satuno nos fijamos en los datos elativos al satélite Rhea. Éste evoluciona po la acción de la fueza de T atacción gavitatoia de Satuno; esta fueza se compota como fueza centípeta, po lo que, al aplica la ª ley de Newton al movimiento de Rhea, queda: G M SM R =M ; la masa de Rhea se R puede simplifica en esta expesión y, como = T, finalmente se llega a M S = 4 3 GT. El peiodo del movimiento de Rhea alededo de Satuno vale: T =4,5(d as)$4 hoas s d a $3600 d a =3,91$10 5 (s). La masa de Satuno es, entonces, 4 M S = $(5,9$10 8 ) 3 6,67$ $(3,91$10 5 ) =5,73$10 6 (kg) R fagm, septiembe 009 { 36 }
37 Física de º Bachilleato Campo gavitatoio Actividad 37 [a] Escibe y comenta la Ley de Gavitación Univesal. [b] Dos planetas esféicos tienen la misma masa, M 1 = M, peo la aceleación de la gavedad en la supeficie del pimeo es cuato veces mayo que en la del segundo, g 1 = 4g. Calcula la elación ente los adios de los planetas, R 1/R, y ente sus densidades, 1 /. [a] Consulta el libo de Física. [b] En pime luga, escibimos las expesiones de la intensidad del campo gavitatoio paa los g 1 = GM 1 R dos planetas: 1. Al impone la condición del enunciado se llega a: ; g = GM 1 R = 4 1 R R R 1 ;. Se compueba, como tiene que se, que en el planeta más pequeño -con la R = 1 R 1 4 R =0,5 misma masa- la intensidad del campo gavitatoio en su supeficie es mayo. En función de la densidad y del tamaño del planeta, la masa del mismo es: M 1 = 4 3 R Las intensidades del campo gavitatoio son, ahoa: g 1 = 4 3G R 1 1. Con la condición g = 4 3 G R 1 del enunciado, se cumpliá: R 1 1 =4R ; = 4R R 1 = 4 0,5 =8. Con las condiciones del enunciado vemos que el planeta más pequeño ha de se el más denso. fagm, septiembe 009 { 37 }
38 Física de º Bachilleato Campo gavitatoio Actividad 38 La elación ente los adios medios de las óbitas de Mate y la Tiea en tono al Sol es R M/R T = 1,53. Calcula el peiodo de la óbita de Mate en tono al Sol (duación del año maciano ). Se ha de cumpli paa los dos planetas la 3ª ley de Keple: los cuadados de los peiodos son popocionales a los cubos de las distancias medias de los planetas al Sol, esto es, T R 3 Tiea = T R 3 Mate R M 3 R T = T M T T ; esta igualdad se puede escibi como sigue: ; se extae la aíz cuadada a los dos miembos de la igualdad: T M =T T R M R T 3/. R M 3/ T R T = M T T ; de donde se deduce que: El peiodo de evolución de la Tiea en tono al Sol es de 1 año; en consecuencia, el peiodo de evolución de Mate alededo del Sol seá: T M =1(año)$(1,53) 3/ =1,89(años). El año maciano dua 1,89 años teestes. fagm, septiembe 009 { 38 }
39 Física de º Bachilleato Campo gavitatoio Actividad 39 La óbita de Plutón en tono al Sol es notablemente excéntica. La elación de distancias máxima y mínima ente su cento y el del Sol (afelio y peihelio) es R a/r p = 5/3. Razonando tus espuestas, calcula la elación (cociente) ente los valoes en el afelio y en el peihelio de las siguientes magnitudes de Plutón: [a] Momento angula especto al cento del Sol. [b] Enegía cinética. [c] Enegía potencial gavitatoia. R p Sol Plutón R a [a] Sobe Plutón está actuando una fueza gavitatoia diigida hacia el cento del Sol. El momento de esta fueza especto dicho punto es ceo, po lo que el momento angula de Plutón, especto al cento del Sol, es constante. Po lo tanto, la elación ente los valoes de L a esta magnitud en el afelio y en el peihelio es igual a la unidad: L p =1. [b] El momento angula de una patícula de masa m, que lleva una apidez v, situada a una distancia del punto de efeencia está dada po: L =mv. Po oto lado, la enegía cinética de dicha patícula vale: E c = 1 mv. De la pimea ecuación, v = m L ; sustituyendo esta expesión en la segunda ecuación se llega a E c = L. m Aplicando esta expesión al caso de Plutón, en el afelio y en el peihelio, se obtiene: E c,a = L a MR a E c,a. Los momento angulaes son iguales, po lo que. E c,p = L p E c,p = R p R a =( 3 5 ) = 9 5 MR p La apidez en el afelio es meno que en el peihelio, lo mismo que la enegía cinética. [c] La enegía potencial gavitatoia se calcula mediante: U = G Mm ; esta magnitud es invesa- U a U p = Rp R a = 3 5 mente popocional a la distancia de Plutón al Sol; po lo tanto,. fagm, septiembe 009 { 39 }
40 Física de º Bachilleato Campo gavitatoio Actividad 40 Io es un satélite de Júpite cuya masa es M io = 8,910 kg y su adio R io = 1,810 6 m. El adio de la óbita, supuesta cicula, en tono a Júpite es = 4,10 8 m. [a] Cuál es el peiodo de otación de Io en tono a Júpite? [b] Detemina la velocidad y la aceleación de Io en su óbita, (módulo y diección). DATOS: G = 6, Nm²kg - ; M Júpite = 1, kg; R Júpite = 6, m. [a] Se aplica la ª ley de Newton al satélite en su óbita cicula. La fueza gavitatoia que ejece Júpite sobe el satélite Ío se compota como fueza centípeta, po lo que G M JM Io =M ; como, la expesión de la ª ley de Newton se puede escibi: Io = T G M J = 4 ; de donde se deduce que ;. 3 T T = GM J T = $(4,$10 8 ) 3 6,67$10 11 $1,90$10 =1,5$10 5 (s) 7 [b] El módulo de la velocidad se obtiene de la aplicación de la ª ley de Newton escita de foma GM J 6,67$10 11 $1,90$10 7 conveniente: G M JM Io v ;. =M Io v = = 4,$10 =1,74$10 4 ( m s) 8 También se puede obtene el valo de la apidez una vez conocido el peiodo: v = T = $4,$108 1,5$10 =1,74$10 4 ( m s). 5 La aceleación de Io coincide con el valo de la intensidad del campo gavitatoio, debido a Júpite, a esa distancia; esto es, a =g=g M J = 6,67$10 11 $1,90$10 7 =0.718 m. (4,$10 8 ) s La diección y el sentido de los vectoes velocidad y aceleación se muestan en la siguiente figua. La velocidad es tangente a la tayectoia y la aceleación, que es centípeta, está diigida hacia el cento de Júpite. Son dos vectoes pependiculaes que están en el mismo plano. v Ío Júpite a fagm, septiembe 009 { 40 }
10.- www.lortizdeo.tk I.E.S. Francisco Grande Covián Campo Gravitatorio mailto:lortizdeo@hotmail.com 27/01/2005 Física 2ªBachiller
 www.lotizdeo.tk I.E.S. Fancisco Gande Covián Campo Gavitatoio mailto:lotizdeo@hotmail.com 7/01/005 Física ªBachille 10.- Un satélite atificial descibe una óbita elíptica, con el cento de la iea en uno
www.lotizdeo.tk I.E.S. Fancisco Gande Covián Campo Gavitatoio mailto:lotizdeo@hotmail.com 7/01/005 Física ªBachille 10.- Un satélite atificial descibe una óbita elíptica, con el cento de la iea en uno
+ + h. 8 v A. = = 2026 m s 1 3 1,3 10 6 m
 m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
CAMPO GRAVITATORIO FCA 10 ANDALUCÍA
 CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
Ejercicios resueltos
 Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
CAMPO GRAVITATORIO FCA 04 ANDALUCÍA
 CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN
 Física P.A.U. GRAVIACIÓN 1 GRAVIACIÓN INRODUCCIÓN MÉODO 1. En geneal: Se dibujan las fuezas que actúan sobe el sistema. Se calcula la esultante po el pincipio de supeposición. Se aplica la ª ley de Newton
Física P.A.U. GRAVIACIÓN 1 GRAVIACIÓN INRODUCCIÓN MÉODO 1. En geneal: Se dibujan las fuezas que actúan sobe el sistema. Se calcula la esultante po el pincipio de supeposición. Se aplica la ª ley de Newton
D.1.- Considere el movimiento de una partícula de masa m bajo la acción de una fuerza central del tipo. n ˆ
 Cuso Mecánica (FI-1A), Listado de ejecicios. Edito: P. Aceituno 34 Escuela de Ingenieía. Facultad de Ciencias Físicas y Matemáticas. Univesidad de Chile. D: FUERZAS CENTRALES Y MOVIMIENTOS PLANETARIOS
Cuso Mecánica (FI-1A), Listado de ejecicios. Edito: P. Aceituno 34 Escuela de Ingenieía. Facultad de Ciencias Físicas y Matemáticas. Univesidad de Chile. D: FUERZAS CENTRALES Y MOVIMIENTOS PLANETARIOS
C. VALENCIANA / SEPTIEMBRE 04. LOGSE / FÍSICA / EXAMEN COMPLETO
 . VALENANA / SEPEMBRE 04. LOGSE / FÍSA / EXAMEN EXAMEN El alumno ealizaá una opción de cada uno de los bloques La puntuación máxima de cada poblema es de puntos, y la de cada cuestión es de,5 puntos. BLOQUE
. VALENANA / SEPEMBRE 04. LOGSE / FÍSA / EXAMEN EXAMEN El alumno ealizaá una opción de cada uno de los bloques La puntuación máxima de cada poblema es de puntos, y la de cada cuestión es de,5 puntos. BLOQUE
Leyes de Kepler. Ley de Gravitación Universal
 Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
a = G m T r T + h 2 a = G r T
 www.clasesalacata.com Ley de la Gavitación Univesal 0.- Gavitación Univesal y Campo Gavitatoio Esta ley fomulada po Newton, afima que la fueza de atacción que expeimentan dos cuepos dotados de masa es
www.clasesalacata.com Ley de la Gavitación Univesal 0.- Gavitación Univesal y Campo Gavitatoio Esta ley fomulada po Newton, afima que la fueza de atacción que expeimentan dos cuepos dotados de masa es
La fuerza gravitatoria entre dos masas viene dada por la ley de gravitación universal de Newton, cuya expresión vectorial es
 LGUNS CUESTIONES TEÓICS SOE LOS TEMS Y.. azone si las siuientes afimaciones son vedadeas o falsas a) El tabajo que ealiza una fueza consevativa sobe una patícula que se desplaza ente dos puntos, es meno
LGUNS CUESTIONES TEÓICS SOE LOS TEMS Y.. azone si las siuientes afimaciones son vedadeas o falsas a) El tabajo que ealiza una fueza consevativa sobe una patícula que se desplaza ente dos puntos, es meno
CAMPO GRAVITATORIO FCA 05 ANDALUCÍA
 CAPO GRAVIAORIO FCA 05 ANDALUCÍA 1. Un satélite descibe una óbita cicula alededo de la iea. Conteste azonadaente a las siguientes peguntas: a) Qué tabajo ealiza la fueza de atacción hacia la iea a lo lago
CAPO GRAVIAORIO FCA 05 ANDALUCÍA 1. Un satélite descibe una óbita cicula alededo de la iea. Conteste azonadaente a las siguientes peguntas: a) Qué tabajo ealiza la fueza de atacción hacia la iea a lo lago
PROBLEMAS CAMPO GRAVITATORIO
 PROBLEMAS CAMPO GRAVITATORIO 1. a) Desde la supeficie de la Tiea se lanza veticalmente hacia aiba un objeto con una velocidad v. Si se despecia el ozamiento, calcule el valo de v necesaio paa que el objeto
PROBLEMAS CAMPO GRAVITATORIO 1. a) Desde la supeficie de la Tiea se lanza veticalmente hacia aiba un objeto con una velocidad v. Si se despecia el ozamiento, calcule el valo de v necesaio paa que el objeto
Examen de Selectividad de Física. Septiembre 2008. Soluciones.
 Depatamento de Física y Química. I. E.. Atenea (.. Reyes, Madid) Examen de electividad de Física. eptiembe 2008. oluciones. Pimea pate Cuestión 1. Calcule el módulo del momento angula de un objeto de 1000
Depatamento de Física y Química. I. E.. Atenea (.. Reyes, Madid) Examen de electividad de Física. eptiembe 2008. oluciones. Pimea pate Cuestión 1. Calcule el módulo del momento angula de un objeto de 1000
CAMPO GRAVITATORIO FCA 06 ANDALUCÍA
 CAMPO AVIAOIO FCA 06 ANDALUCÍA 1.- Si po alguna causa la iea edujese su adio a la itad anteniendo su asa, azone cóo se odificaían: a) La intensidad del capo gavitatoio en su supeficie. b) Su óbita alededo
CAMPO AVIAOIO FCA 06 ANDALUCÍA 1.- Si po alguna causa la iea edujese su adio a la itad anteniendo su asa, azone cóo se odificaían: a) La intensidad del capo gavitatoio en su supeficie. b) Su óbita alededo
CUESTIONES Y PROBLEMAS DE CAMPO ELÉCTRICO. Ejercicio nº1 Cómo se manifiesta la propiedad de la materia denominada carga eléctrica?
 UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
Actividades del final de la unidad
 Actividades del final de la unidad. Indica cuál de las siguientes afimaciones es falsa: a) En la época de Aistóteles ya se aceptaba que la iea ea esféica. b) La estimación del adio teeste que llevó a cabo
Actividades del final de la unidad. Indica cuál de las siguientes afimaciones es falsa: a) En la época de Aistóteles ya se aceptaba que la iea ea esféica. b) La estimación del adio teeste que llevó a cabo
b) La velocidad de escape se calcula con la siguiente expresión:
 ADID / JUNIO 0. LOGSE / FÍSICA / CAPO GAVIAOIO PIEA PAE CUESIÓN Un planeta esféico tiene un adio de 000 km, y la aceleación de la gavedad en su supeficie es 6 m/s. a) Cuál es su densidad media? b) Cuál
ADID / JUNIO 0. LOGSE / FÍSICA / CAPO GAVIAOIO PIEA PAE CUESIÓN Un planeta esféico tiene un adio de 000 km, y la aceleación de la gavedad en su supeficie es 6 m/s. a) Cuál es su densidad media? b) Cuál
avance de un sacacorchos que gira como lo hacemos para llevar el primer vector sobre el segundo por el
 /5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
/5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
Capitulo 9: Leyes de Kepler, Gravitación y Fuerzas Centrales
 Capitulo 9: Leyes de Keple, Gavitación y Fuezas Centales Índice. Las 3 leyes de Keple 2. Campo gavitacional 4 3. Consevación de enegía 6 4. Movimiento cicula 8 5. Difeentes tayectoias 0 6. Demosta Leyes
Capitulo 9: Leyes de Keple, Gavitación y Fuezas Centales Índice. Las 3 leyes de Keple 2. Campo gavitacional 4 3. Consevación de enegía 6 4. Movimiento cicula 8 5. Difeentes tayectoias 0 6. Demosta Leyes
Ejercicios de Gravitación
 jecicios de Gavitación Seway.5: Calcule la magnitud y diección del campo gavitacional en un punto P sobe la bisectiz pependicula de la ecta que une dos cuepos de igual masa sepaados po una distancia a,
jecicios de Gavitación Seway.5: Calcule la magnitud y diección del campo gavitacional en un punto P sobe la bisectiz pependicula de la ecta que une dos cuepos de igual masa sepaados po una distancia a,
Es el producto escalar de la fuerza aplicada al cuerpo por el vector r r Por lo tanto es una magnitud escalar.
 TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
Tema 2. Sistemas conservativos
 Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
BLOQUE 1: INTERACCIÓN GRAVITATORIA
 BLOQUE 1: INTERACCIÓN GRAVITATORIA 1.-EL MOVIMIENTO DE LOS PLANETAS A TRAVÉS DE LA HISTORIA La inteacción gavitatoia tiene una gan influencia en el movimiento de los cuepos, tanto de los que se encuentan
BLOQUE 1: INTERACCIÓN GRAVITATORIA 1.-EL MOVIMIENTO DE LOS PLANETAS A TRAVÉS DE LA HISTORIA La inteacción gavitatoia tiene una gan influencia en el movimiento de los cuepos, tanto de los que se encuentan
Potencial eléctrico. Trabajo y energía potencial en el campo eléctrico. Potencial de una carga puntual: Principio de superposición
 Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Parte 3: Electricidad y Magnetismo
 Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
IES Fco Ayala de Granada Junio de 2014 (Modelo 1) Soluciones Germán-Jesús Rubio Luna. Opción A. Ejercicio 2 opción A, modelo_1 Junio 2014
 IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
Examen de Selectividad de Física. Junio 2009. Soluciones.
 Depatamento de Física y Química. I. E. S. Atenea (S. S. Reyes, Madid) Examen de Selectividad de Física. Junio 009. Soluciones. Pimea pate Cuestión 1.- Un satélite atificial de 500 kg que descibe una óbita
Depatamento de Física y Química. I. E. S. Atenea (S. S. Reyes, Madid) Examen de Selectividad de Física. Junio 009. Soluciones. Pimea pate Cuestión 1.- Un satélite atificial de 500 kg que descibe una óbita
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
Parametrizando la epicicloide
 1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
Ejercicios resueltos
 Ejecicios esueltos Boletín 1 Leyes de Keple y Ley de gavitación univesal Ejecicio 1 Dos planetas de masas iguales obitan alededo de una estella de masa mucho mayo. El planeta 1 descibe una óbita cicula
Ejecicios esueltos Boletín 1 Leyes de Keple y Ley de gavitación univesal Ejecicio 1 Dos planetas de masas iguales obitan alededo de una estella de masa mucho mayo. El planeta 1 descibe una óbita cicula
L Momento angular de una partícula de masa m
 Campo gavitatoio Momento de un vecto con especto a un punto: M El momento del vecto con especto al punto O se define como el poducto vectoial M = O Es un vecto pependicula al plano fomado po los vectoes
Campo gavitatoio Momento de un vecto con especto a un punto: M El momento del vecto con especto al punto O se define como el poducto vectoial M = O Es un vecto pependicula al plano fomado po los vectoes
v L G M m =m v2 r D M S r D
 Poblemas de Campo Gavitatoio 1 Calcula la velocidad media de la iea en su óbita alededo del ol y la de la luna en su óbita alededo de la iea, sabiendo que el adio medio de la óbita luna es 400 veces meno
Poblemas de Campo Gavitatoio 1 Calcula la velocidad media de la iea en su óbita alededo del ol y la de la luna en su óbita alededo de la iea, sabiendo que el adio medio de la óbita luna es 400 veces meno
2.7 Cilindros, conos, esferas y pirámides
 UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
CAMPO ELÉCTRICO 7.1. FENÓMENOS DE ELECTRIZACIÓN 7.2. LEY DE COULOMB
 7 CAMPO ELÉCTRICO 7.. FENÓMENOS DE ELECTRIZACIÓN. Un péndulo electostático es un dispositivo fomado po una esfea ligea, de mateial aislante, suspendida de un hilo de masa despeciable. Utilizando ese dispositivo,
7 CAMPO ELÉCTRICO 7.. FENÓMENOS DE ELECTRIZACIÓN. Un péndulo electostático es un dispositivo fomado po una esfea ligea, de mateial aislante, suspendida de un hilo de masa despeciable. Utilizando ese dispositivo,
PROBLEMAS DE ELECTROESTÁTICA
 PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
www.fisicaeingenieria.es Vectores y campos
 www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
5. Sistemas inerciales y no inerciales
 5. Sistemas ineciales y no ineciales 5.1. Sistemas ineciales y pincipio de elatividad de Galileo El conjunto de cuepos especto de los cuales se descibe el movimiento se denomina sistema de efeencia, y
5. Sistemas ineciales y no ineciales 5.1. Sistemas ineciales y pincipio de elatividad de Galileo El conjunto de cuepos especto de los cuales se descibe el movimiento se denomina sistema de efeencia, y
L r p. Teniendo en cuenta que p es el momento lineal (masa por el vector velocidad) la expresión anterior nos queda: L r mv m r v. d L dr dv dt dt dt
 EOEA DE CONSEVACIÓN DE OENO ANGUA: El momento angula se define como: p CASE 4.- EYES DE CONSEVACIÓN eniendo en cuenta que p es el momento lineal (masa po el vecto velocidad) la expesión anteio nos queda:
EOEA DE CONSEVACIÓN DE OENO ANGUA: El momento angula se define como: p CASE 4.- EYES DE CONSEVACIÓN eniendo en cuenta que p es el momento lineal (masa po el vecto velocidad) la expesión anteio nos queda:
Sustituyendo los valores que nos da el problema obtenemos el siguiente valor para la fuerza:
 1. Caga eléctica 2. Fueza electostática 3. Campo eléctico 4. Potencial electostático 5. Enegía potencial electostática 6. Repesentación de campos elécticos 7. Movimiento de cagas elécticas en el seno de
1. Caga eléctica 2. Fueza electostática 3. Campo eléctico 4. Potencial electostático 5. Enegía potencial electostática 6. Repesentación de campos elécticos 7. Movimiento de cagas elécticas en el seno de
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES
 PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
TEMA 2.- Campo gravitatorio
 ema.- Campo gavitatoio EMA.- Campo gavitatoio CUESIONES.- a) Una masa m se encuenta dento del campo gavitatoio ceado po ota masa M. Si se mueve espontáneamente desde un punto A hasta oto B, cuál de los
ema.- Campo gavitatoio EMA.- Campo gavitatoio CUESIONES.- a) Una masa m se encuenta dento del campo gavitatoio ceado po ota masa M. Si se mueve espontáneamente desde un punto A hasta oto B, cuál de los
CANARIAS / SEPTIEMBRE 03. LOGSE / FÍSICA / EXAMEN COMPLETO
 De las dos opciones popuestas, sólo hay que desaolla una opción completa. Cada poblema coecto vale po tes puntos. Cada cuestión coecta vale po un punto. Poblemas OPCIÓN A.- Un satélite descibe una óbita
De las dos opciones popuestas, sólo hay que desaolla una opción completa. Cada poblema coecto vale po tes puntos. Cada cuestión coecta vale po un punto. Poblemas OPCIÓN A.- Un satélite descibe una óbita
CAPITULO VI FUERZAS CENTRALES. " Qué es lo que hace que los planetas giren en torno al Sol?
 FUEZAS CENALES CAPIULO VI " Qué es lo que hace que los planetas gien en tono al Sol? En los tiempos de Keple algunas pesonas contestaban esta pegunta diciendo que había ángeles detás de ellos, agitando
FUEZAS CENALES CAPIULO VI " Qué es lo que hace que los planetas gien en tono al Sol? En los tiempos de Keple algunas pesonas contestaban esta pegunta diciendo que había ángeles detás de ellos, agitando
[b] La ecuación de la velocidad se obtiene derivando, con respecto al tiempo, la ecuación de la
![[b] La ecuación de la velocidad se obtiene derivando, con respecto al tiempo, la ecuación de la [b] La ecuación de la velocidad se obtiene derivando, con respecto al tiempo, la ecuación de la](/thumbs/75/72620212.jpg) Nombe y apellidos: Puntuación: 1. Pimeo vetical, luego hoizontal Un muelle, de masa despeciable, se defoma 20 cm cuando se le cuelga un cuepo de 1,0 kg de masa (figua 1). A continuación, se coloca sin
Nombe y apellidos: Puntuación: 1. Pimeo vetical, luego hoizontal Un muelle, de masa despeciable, se defoma 20 cm cuando se le cuelga un cuepo de 1,0 kg de masa (figua 1). A continuación, se coloca sin
Soluciones de la Tarea #6 de Física I
 Soluciones de la Taea #6 de Física I Tomás Rocha Rinza 4 de octube de 006 1. Puesto que la tayectoia del satélite alededo de la Tiea es cicula, entonces ocue en un plano. Si se considea a la Tiea fija
Soluciones de la Taea #6 de Física I Tomás Rocha Rinza 4 de octube de 006 1. Puesto que la tayectoia del satélite alededo de la Tiea es cicula, entonces ocue en un plano. Si se considea a la Tiea fija
CANARIAS / SEPTIEMBRE 02. LOGSE / FÍSICA / EXAMEN COMPLETO
 CANAIAS / SEPTIEMBE 0. LOGSE / FÍSICA / EXAMEN COMPLETO De las dos opciones popuestas, sólo hay que desaolla una opción completa. Cada poblema coecto vale po tes puntos. Cada cuestión coecta vale po un
CANAIAS / SEPTIEMBE 0. LOGSE / FÍSICA / EXAMEN COMPLETO De las dos opciones popuestas, sólo hay que desaolla una opción completa. Cada poblema coecto vale po tes puntos. Cada cuestión coecta vale po un
[b] La ecuación de la velocidad se obtiene al derivar la elongación con respecto al tiempo: v(t) = dx
![[b] La ecuación de la velocidad se obtiene al derivar la elongación con respecto al tiempo: v(t) = dx [b] La ecuación de la velocidad se obtiene al derivar la elongación con respecto al tiempo: v(t) = dx](/thumbs/52/30574321.jpg) Nombe y apellidos: Puntuación:. Las gáficas del oscilado amónico En la figua se muesta al gáfica elongacióntiempo de una patícula de,5 kg de masa que ealiza una oscilación amónica alededo del oigen de
Nombe y apellidos: Puntuación:. Las gáficas del oscilado amónico En la figua se muesta al gáfica elongacióntiempo de una patícula de,5 kg de masa que ealiza una oscilación amónica alededo del oigen de
UNIVERSIDAD DE GRANADA PRUEBA DE ACCESO A LA UNIVERSIDAD TERRITORIO DEL MINISTERIO DE EDUCACIÓN CURSO
 UNIVERSIDAD DE GRANADA PRUEBA DE AESO A LA UNIVERSIDAD ERRIORIO DEL MINISERIO DE EDUAIÓN URSO 00-0 ÍSIA Instucciones: a) Duación: hoa y 30 minutos. b) Debe desaolla tes poblemas (uno de campo gavitatoio
UNIVERSIDAD DE GRANADA PRUEBA DE AESO A LA UNIVERSIDAD ERRIORIO DEL MINISERIO DE EDUAIÓN URSO 00-0 ÍSIA Instucciones: a) Duación: hoa y 30 minutos. b) Debe desaolla tes poblemas (uno de campo gavitatoio
2 Campo gravitatorio. Actividades del interior de la unidad
 Campo gavitatoio Actividades del inteio de la unidad. Enumea las cuato inteacciones fundamentales de la natualeza. Las inteacciones fundamentales son cuato: gavitatoia, electomagnética, nuclea fuete y
Campo gavitatoio Actividades del inteio de la unidad. Enumea las cuato inteacciones fundamentales de la natualeza. Las inteacciones fundamentales son cuato: gavitatoia, electomagnética, nuclea fuete y
[a] Para un tubo abierto la menor frecuencia corresponde a la frecuencia fundamental, dada por f 1 = v. . La longitud de onda es, entonces,
![[a] Para un tubo abierto la menor frecuencia corresponde a la frecuencia fundamental, dada por f 1 = v. . La longitud de onda es, entonces, [a] Para un tubo abierto la menor frecuencia corresponde a la frecuencia fundamental, dada por f 1 = v. . La longitud de onda es, entonces,](/thumbs/85/91836336.jpg) Física de º Bachilleato Junio de 0 Opción A. Ejecicio Considee dos tubos sonoos de la misma longitud, L =,36 m, el pimeo con sus dos extemos abietos a la atmósfea y el segundo con uno abieto y oto ceado.
Física de º Bachilleato Junio de 0 Opción A. Ejecicio Considee dos tubos sonoos de la misma longitud, L =,36 m, el pimeo con sus dos extemos abietos a la atmósfea y el segundo con uno abieto y oto ceado.
INTERACCIÓN ELECTROMAGNÉTICA ELECTROMAGNETISMO. Campo magnético creado por un conductor
 TERACCÓ ELECTROMAGÉTCA ELECTROMAGETSMO ES La Magdalena. Avilés. Astuias La unión electicidad-magnetismo tiene una fecha: 180. Ese año Oested ealizó su famoso expeimento (ve figua) en el cual hacía cicula
TERACCÓ ELECTROMAGÉTCA ELECTROMAGETSMO ES La Magdalena. Avilés. Astuias La unión electicidad-magnetismo tiene una fecha: 180. Ese año Oested ealizó su famoso expeimento (ve figua) en el cual hacía cicula
Campo gravitatorio: cuestiones PAU
 Campo gavitatoio: cuestiones PU 3. Descibe bevemente las teoías que se han sucedido a lo lago de la histoia paa explica la estuctua del sistema sola. La obsevación del cielo y sus astos ha sido, desde
Campo gavitatoio: cuestiones PU 3. Descibe bevemente las teoías que se han sucedido a lo lago de la histoia paa explica la estuctua del sistema sola. La obsevación del cielo y sus astos ha sido, desde
TEMA3: CAMPO ELÉCTRICO
 FÍIC º BCHILLERTO. CMPO ELÉCTRICO. TEM3: CMPO ELÉCTRICO o Natualeza eléctica de la mateia. o Ley de Coulomb vs Ley de Newton. o Pincipio de supeposición. o Intensidad del campo elético. o Líneas del campo
FÍIC º BCHILLERTO. CMPO ELÉCTRICO. TEM3: CMPO ELÉCTRICO o Natualeza eléctica de la mateia. o Ley de Coulomb vs Ley de Newton. o Pincipio de supeposición. o Intensidad del campo elético. o Líneas del campo
rad/s EXAMEN FÍSICA PAEG UCLM. JUNIO 2013. SOLUCIONARIO
 EXAMEN FÍSICA PAEG UCLM. JUNIO 01. SOLUCIONARIO OPCIÓN A. PROBLEMA 1 Una onda tansvesal se popaga po una cueda tensa fija po sus extemos con una velocidad de 80 m/s, y al eflejase se foma el cuato amónico
EXAMEN FÍSICA PAEG UCLM. JUNIO 01. SOLUCIONARIO OPCIÓN A. PROBLEMA 1 Una onda tansvesal se popaga po una cueda tensa fija po sus extemos con una velocidad de 80 m/s, y al eflejase se foma el cuato amónico
b) ; como el trabajo no conservativo es nulo, la energía mecánica se conserva, es igual en el perihelio y en el afelio.
 Depataento de ísica y Quíica 1 PAU ísica, septiebe 2010. ase específica. OPCIÓN A Cuestión 1. - Un coeta se ueve en una óbita elíptica alededo del Sol. Explique en qué punto de su óbita, afelio (punto
Depataento de ísica y Quíica 1 PAU ísica, septiebe 2010. ase específica. OPCIÓN A Cuestión 1. - Un coeta se ueve en una óbita elíptica alededo del Sol. Explique en qué punto de su óbita, afelio (punto
Tema 2. Sistemas conservativos
 Tema. Sistemas consevativos Cuata pate: Movimiento planetaio. Satélites A) Ecuaciones del movimiento Suponemos que uno de los cuepos, de masa M mucho mayo que m, se encuenta en eposo en el oigen de coodenadas
Tema. Sistemas consevativos Cuata pate: Movimiento planetaio. Satélites A) Ecuaciones del movimiento Suponemos que uno de los cuepos, de masa M mucho mayo que m, se encuenta en eposo en el oigen de coodenadas
MAGNITUDES VECTORIALES:
 Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
GALICIA / JUNIO 03. LOGSE / FÍSICA / EXAMEN COMPLETO
 GALICIA / JUNIO 3. LOGSE / FÍSICA / EXAMEN COMPLEO El examen de física de las P.A.U. pesenta dos opciones de semejante nivel de dificultad. Cada opción consta de tes pates difeentes(poblemas, cuestiones
GALICIA / JUNIO 3. LOGSE / FÍSICA / EXAMEN COMPLEO El examen de física de las P.A.U. pesenta dos opciones de semejante nivel de dificultad. Cada opción consta de tes pates difeentes(poblemas, cuestiones
r 2 F 2 E = E C +V = 1 2 mv 2 GMm J O = mr 2 dθ dt = mr 2 ω = mrv θ v θ = J O mr E = O 2mr GMm 2 r
 Física paa Ciencias e Ingenieía 18.1 18.1 Leyes de Keple Supongamos que se ha lanzado un satélite atificial de masa m, sometido al campo gavitatoio teeste, de tal manea que su enegía mecánica sea negativa.
Física paa Ciencias e Ingenieía 18.1 18.1 Leyes de Keple Supongamos que se ha lanzado un satélite atificial de masa m, sometido al campo gavitatoio teeste, de tal manea que su enegía mecánica sea negativa.
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO
 PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
Solución a los ejercicios de vectores:
 Tema 0: Solución ejecicios de intoducción vectoes Solución a los ejecicios de vectoes: Nota : Estas soluciones pueden tene eoes eatas (es un ollo escibios las soluciones bonitas con el odenado), así que
Tema 0: Solución ejecicios de intoducción vectoes Solución a los ejecicios de vectoes: Nota : Estas soluciones pueden tene eoes eatas (es un ollo escibios las soluciones bonitas con el odenado), así que
U.D. 3. I NTERACCIÓN GRAVITATORIA
 U.D. 3. I NERACCIÓN GRAVIAORIA RESUMEN Ley de gavitación univesal: odos los cuepos se ataen con una fueza diectamente popocional al poducto de sus masas e invesamente popocional al cuadado de la distancia
U.D. 3. I NERACCIÓN GRAVIAORIA RESUMEN Ley de gavitación univesal: odos los cuepos se ataen con una fueza diectamente popocional al poducto de sus masas e invesamente popocional al cuadado de la distancia
I.E.S. Al-Ándalus. Dpto. de Física-Química. Física 2º Bachillerato. Tema 2. Int. Gravitatoria - 1 - TEMA 2: INTERACCIÓN GRAVITATORIA
 I.E.. l-ándalus. Dpto. de Física-Química. Física º achilleato. Tema. Int. Gavitatoia - 1 - TE : INTECCIÓN GVITTOI.1 Inteacción avitatoia; ley de avitación univesal. Campo y potencial avitatoios; eneía
I.E.. l-ándalus. Dpto. de Física-Química. Física º achilleato. Tema. Int. Gavitatoia - 1 - TE : INTECCIÓN GVITTOI.1 Inteacción avitatoia; ley de avitación univesal. Campo y potencial avitatoios; eneía
5.2 Capítulo 5. FUERZAS CENTRALES Y ÓRBITAS GRAVITATORIAS
 5.2 Capítulo 5. FUERZAS CENTRALES Y ÓRBITAS GRAVITATORIAS descitos en una efeencia inecial (I) po sus vectoes de posición 0 y 1 espectivamente. I m 1 1 F 10 1 F 01 m 1 0 0 0 Figua 5.1: Sistema binaio aislado
5.2 Capítulo 5. FUERZAS CENTRALES Y ÓRBITAS GRAVITATORIAS descitos en una efeencia inecial (I) po sus vectoes de posición 0 y 1 espectivamente. I m 1 1 F 10 1 F 01 m 1 0 0 0 Figua 5.1: Sistema binaio aislado
Deflexión de rayos luminosos causada por un cuerpo en rotación
 14 Defleión de ayos luminosos causada po un cuepo en otación 114 Intoducción Cuando un ayo luminoso pasa po la cecanía de un cuepo se ve obligado a abandona su tayectoia ectilínea y cuvase más o menos
14 Defleión de ayos luminosos causada po un cuepo en otación 114 Intoducción Cuando un ayo luminoso pasa po la cecanía de un cuepo se ve obligado a abandona su tayectoia ectilínea y cuvase más o menos
FÓRMULAS Y DEDUCCIONES QUE HAY QUE SABER. Mm v GM
 CLASE : LEY DE LA GRAVIACIÓN UNIVERSAL. SAÉLIES I FÓRMULAS Y DEDUCCIONES QUE HAY QUE SABER VELOCIDAD ORBIAL DE UN SAÉLIE: g c gr Mm v 0 F F G m v PERIODO DE UN SAÉLIE: v g0r PESO DE UN SAÉLIE EN UNA ÓRBIA:
CLASE : LEY DE LA GRAVIACIÓN UNIVERSAL. SAÉLIES I FÓRMULAS Y DEDUCCIONES QUE HAY QUE SABER VELOCIDAD ORBIAL DE UN SAÉLIE: g c gr Mm v 0 F F G m v PERIODO DE UN SAÉLIE: v g0r PESO DE UN SAÉLIE EN UNA ÓRBIA:
6.5 ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS
 6.. Gáficas de ectas usando m b Po ejemplo, paa gafica la ecta Maca el valo de b (odenada al oigen) sobe el eje, es deci el punto (0,). A pati de ese punto, como la pendiente es, se toma una unidad a la
6.. Gáficas de ectas usando m b Po ejemplo, paa gafica la ecta Maca el valo de b (odenada al oigen) sobe el eje, es deci el punto (0,). A pati de ese punto, como la pendiente es, se toma una unidad a la
INTRODUCCION AL ANALISIS VECTORIAL
 JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
Solución al examen de Física
 Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
Tema 6: Campo Eléctrico
 Física º Bachilleato Tema 6: Campo Eléctico 6.1.- Intoducción En el capítulo anteio vimos que cuando intoducimos una patícula en el espacio vacío, ésta lo modifica, haciendo cambia su geometía, de modo
Física º Bachilleato Tema 6: Campo Eléctico 6.1.- Intoducción En el capítulo anteio vimos que cuando intoducimos una patícula en el espacio vacío, ésta lo modifica, haciendo cambia su geometía, de modo
mv G 0 mv G mv G r GM Mm Mm Mm E E E E E Mm Mm Mm Mm 1 1 G E G E G G GMm
 FÓRMULAS Y DDUCCIONS QU HAY QU SABR VLOCIDAD D SCAP: (velocidad mínima con la que hay que lanza un objeto desde la supeficie de un planeta paa que escape a su atacción gavitatoia) M1 M c1 p1 0 1 Mm 1 Mm
FÓRMULAS Y DDUCCIONS QU HAY QU SABR VLOCIDAD D SCAP: (velocidad mínima con la que hay que lanza un objeto desde la supeficie de un planeta paa que escape a su atacción gavitatoia) M1 M c1 p1 0 1 Mm 1 Mm
Interacción gravitatoria
 Inteacción gavitatoia H. O. Di Rocco I.F.A.S., Facultad de Cs. Exactas, U.N.C.P.B.A. June 5, 00 Abstact Tatamos en esta clase de oto de los modelos fundamentales de la Física toda: el movimiento en campos
Inteacción gavitatoia H. O. Di Rocco I.F.A.S., Facultad de Cs. Exactas, U.N.C.P.B.A. June 5, 00 Abstact Tatamos en esta clase de oto de los modelos fundamentales de la Física toda: el movimiento en campos
EXAMEN FÍSICA 2º BACHILLERATO TEMA 1: CAMPO GRAVITATORIO
 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
Tema 3. Campo eléctrico
 Tema 3 Campo eléctico Pogama 1. Inteacción eléctica. Campo eléctico.. Repesentación mediante líneas de campo. Flujo eléctico: Ley de Gauss. 3. Enegía y potencial elécticos. Supeficies equipotenciales.
Tema 3 Campo eléctico Pogama 1. Inteacción eléctica. Campo eléctico.. Repesentación mediante líneas de campo. Flujo eléctico: Ley de Gauss. 3. Enegía y potencial elécticos. Supeficies equipotenciales.
Física 2º Bacharelato
 Física º Bachaelato DEPARTAMENTO DE FÍSICA E QUÍMICA Ondas y gavitación 14/1/07 Nombe: Poblema 1. Un satélite de 100 kg tada 100 minutos en descibi una óbita cicula alededo de la Tiea. Calcula: a) La enegía
Física º Bachaelato DEPARTAMENTO DE FÍSICA E QUÍMICA Ondas y gavitación 14/1/07 Nombe: Poblema 1. Un satélite de 100 kg tada 100 minutos en descibi una óbita cicula alededo de la Tiea. Calcula: a) La enegía
IES Rey Fernando VI San Fernando de Henares Departamento de Física y Química. Problemas Resueltos Segunda Parte. Campo Gravitatorio Fuerzas Centrales
 IES Rey Fenando VI San Fenando de Henaes Depatamento de Física y Química Poblemas Resueltos Segunda Pate Campo Gavitatoio Fuezas Centales Pofeso : Jesús Millán Cespo Gupo : Fisica o Bachilleato Fecha :
IES Rey Fenando VI San Fenando de Henaes Depatamento de Física y Química Poblemas Resueltos Segunda Pate Campo Gavitatoio Fuezas Centales Pofeso : Jesús Millán Cespo Gupo : Fisica o Bachilleato Fecha :
Apéndice 4. Introducción al cálculo vectorial. Apéndice 2. Tabla de derivadas y de integrales inmediatas. Ecuaciones de la trigonometría
 Apéndices Apéndice 1. Intoducción al cálculo vectoial Apéndice. Tabla de deivadas y de integales inmediatas Apéndice 3. Apéndice 4. Ecuaciones de la tigonometía Sistema peiódico de los elementos Apéndice
Apéndices Apéndice 1. Intoducción al cálculo vectoial Apéndice. Tabla de deivadas y de integales inmediatas Apéndice 3. Apéndice 4. Ecuaciones de la tigonometía Sistema peiódico de los elementos Apéndice
X I OLIMPIADA NACIONAL DE FÍSICA
 X I LIMPIADA NACINAL D FÍSICA FAS LCAL - UNIVSIDADS D GALICIA - 18 de Febeo de 2000 APLLIDS...NMB... CNT... PUBA BJTIVA 1) Al medi la masa de una esfea se obtuvieon los siguientes valoes (en gamos): 4,1
X I LIMPIADA NACINAL D FÍSICA FAS LCAL - UNIVSIDADS D GALICIA - 18 de Febeo de 2000 APLLIDS...NMB... CNT... PUBA BJTIVA 1) Al medi la masa de una esfea se obtuvieon los siguientes valoes (en gamos): 4,1
Soluciones ejercicios
 Soluciones ejecicios Capítulo 1 adie es pefecto, luego si encuenta eoes, tenga la gentileza de infomanos Ejecicio 1.1 Un cuepo descibe una óbita cicula de adio R =100 m en tono a un punto fijo con apidez
Soluciones ejecicios Capítulo 1 adie es pefecto, luego si encuenta eoes, tenga la gentileza de infomanos Ejecicio 1.1 Un cuepo descibe una óbita cicula de adio R =100 m en tono a un punto fijo con apidez
BLOQUE II - CUESTIONES Opción A Explica mediante un ejemplo el transporte de energía en una onda. Existe un transporte efectivo de masa?
 EXAMEN COMPLETO El alumno ealizaá una opción de cada uno de los bloques La puntuación máxima de cada poblema es de puntos, y la de cada cuestión es de 1,5 puntos. BLOQUE I Un satélite atificial de 500
EXAMEN COMPLETO El alumno ealizaá una opción de cada uno de los bloques La puntuación máxima de cada poblema es de puntos, y la de cada cuestión es de 1,5 puntos. BLOQUE I Un satélite atificial de 500
TRABAJO DE LABORATORIO Nº 2: Potencial Eléctrico Mapa de Campo Eléctrico
 Univesidad Nacional del Nodeste Facultad de Ingenieía Cáteda: Física III Pofeso Adjunto: Ing. Atuo Castaño Jefe de Tabajos Pácticos: Ing. Cesa Rey Auiliaes: Ing. Andés Mendivil, Ing. José Epucci, Ing.
Univesidad Nacional del Nodeste Facultad de Ingenieía Cáteda: Física III Pofeso Adjunto: Ing. Atuo Castaño Jefe de Tabajos Pácticos: Ing. Cesa Rey Auiliaes: Ing. Andés Mendivil, Ing. José Epucci, Ing.
PROBLEMAS DE SATÉLITES Ejemplos de resolución con la hoja de cálculo: «SatelitesEs.ods».
 Física P.A.U. PROBLEMAS DE SATÉLITES 1 PROBLEMAS DE SATÉLITES Ejemplos de esolución con la hoja de cálculo: «SatelitesEs.ods». 1. Un satélite atificial de 64,5 kg gia alededo de la Tiea en una óbita cicula
Física P.A.U. PROBLEMAS DE SATÉLITES 1 PROBLEMAS DE SATÉLITES Ejemplos de esolución con la hoja de cálculo: «SatelitesEs.ods». 1. Un satélite atificial de 64,5 kg gia alededo de la Tiea en una óbita cicula
INDUCCIÓN ELECTROMAGNÉTCA Y ENERGÍA DEL CAMPO MAGNÉTICO
 NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
a) Datos extraídos: = m R m =3, = 9, = h s R s + R m g 0m = 3,7 m s -2
 P1.- Un satélite de 500 kg de asa se ueve alededo de Mate, descibiendo una óbita cicula a 6 10 6 de su supeficie. abiendo que la aceleación de la gavedad en la supeficie de Mate es 3,7 /s y que su adio
P1.- Un satélite de 500 kg de asa se ueve alededo de Mate, descibiendo una óbita cicula a 6 10 6 de su supeficie. abiendo que la aceleación de la gavedad en la supeficie de Mate es 3,7 /s y que su adio
TEMA5 : gravitación Capitulo 2. Potencial
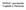 TEMA5 : gavitación Capitulo. Potencial Intoducción TEMA 5: Gavitación Capítulo. Potencial Enegía potencial gavitacional Velocidad de escape Agujeos negos Movimiento de satélites Maeas Enegía potencial
TEMA5 : gavitación Capitulo. Potencial Intoducción TEMA 5: Gavitación Capítulo. Potencial Enegía potencial gavitacional Velocidad de escape Agujeos negos Movimiento de satélites Maeas Enegía potencial
Modelo Pregunta 3A. El campo electrostático creado por una carga puntual q, situada en el
 Modelo 2014. Pegunta 3A. El campo electostático ceado po una caga puntual q, situada en el 9 1 oigen de coodenadas, viene dado po la expesión: E = u 2 N C, donde se expesa en m y u es un vecto unitaio
Modelo 2014. Pegunta 3A. El campo electostático ceado po una caga puntual q, situada en el 9 1 oigen de coodenadas, viene dado po la expesión: E = u 2 N C, donde se expesa en m y u es un vecto unitaio
100 Cuestiones de Selectividad
 Física de º Bachilleato 100 Cuestiones de Selectividad 1.- a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. (And-010-P1) La velocidad de escape es la mínima velocidad
Física de º Bachilleato 100 Cuestiones de Selectividad 1.- a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. (And-010-P1) La velocidad de escape es la mínima velocidad
TEMA 3 MOVIMIENTO CIRCULAR Y GRAVITACIÓN UNIVERSAL
 EMA 3 MOIMIENO CICULA Y GAIACIÓN UNIESAL El movimiento cicula unifome (MCU) Movimiento cicula unifome es el movimiento de un cuepo que tiene po tayectoia una cicunfeencia y descibe acos iguales en tiempos
EMA 3 MOIMIENO CICULA Y GAIACIÓN UNIESAL El movimiento cicula unifome (MCU) Movimiento cicula unifome es el movimiento de un cuepo que tiene po tayectoia una cicunfeencia y descibe acos iguales en tiempos
FORMACIÓN DE IMÁGENES EN ÓPTICA ADAPTATIVA
 Univesidad de Cantabia Tesis Doctoal FORMACIÓN DE IMÁGENES EN ÓPTICA ADAPTATIVA Vidal Fenández Canales Capítulo 1 LA TURBULENCIA ATMOSFÉRICA La atmósfea no se compota como un medio homogéneo paa la popagación
Univesidad de Cantabia Tesis Doctoal FORMACIÓN DE IMÁGENES EN ÓPTICA ADAPTATIVA Vidal Fenández Canales Capítulo 1 LA TURBULENCIA ATMOSFÉRICA La atmósfea no se compota como un medio homogéneo paa la popagación
Derivando dos veces respecto del tiempo obtenemos la aceleración del cuerpo:
 MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
VECTORES, DERIVADAS, INTEGRALES
 Física Tema 0-1 º Bachilleato Vectoes, deivadas, integales Tema 0 VECTORES, DERIVADAS, INTEGRALES 1.- Vectoes. Componentes de un vecto.- Suma y difeencia de vectoes 3.- Poducto de un vecto po un númeo
Física Tema 0-1 º Bachilleato Vectoes, deivadas, integales Tema 0 VECTORES, DERIVADAS, INTEGRALES 1.- Vectoes. Componentes de un vecto.- Suma y difeencia de vectoes 3.- Poducto de un vecto po un númeo
IES Al-Ándalus. Dpto. Física y Química. Curso 2004/05 Física 2º Bachillerato - 1 -
 IS Al-Ándalus. Dpto. Física y Quíica. Cuso 4/5 Física º Bachilleato - - FÍSICA º BACHIAO. XA AS 4, 5 - - 5 OPCIÓ A:. a) Caacteísticas de la inteacción anética. Difeencias con la inteacción electostática.
IS Al-Ándalus. Dpto. Física y Quíica. Cuso 4/5 Física º Bachilleato - - FÍSICA º BACHIAO. XA AS 4, 5 - - 5 OPCIÓ A:. a) Caacteísticas de la inteacción anética. Difeencias con la inteacción electostática.
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
Diferencia de potencial y potencial eléctricos. En el campo gravitatorio.
 Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Problemas de Física 1 o Bachillerato
 Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Campo eléctrico. Introducción a la Física Ambiental. Tema 7. Tema 7.- Campo eléctrico.
 Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
2º de Bachillerato Interacción Gravitatoria
 Física EA º de Bacilleato Inteacción avitatoia.- Aveiua cuál seía la duación del año teeste en el caso supuesto que la iea se acecaa al Sol de manea que la distancia fuea un 0 % meno que la eal. Y si se
Física EA º de Bacilleato Inteacción avitatoia.- Aveiua cuál seía la duación del año teeste en el caso supuesto que la iea se acecaa al Sol de manea que la distancia fuea un 0 % meno que la eal. Y si se
