Multiplicar por la potencia de 10 adecuada para convertirlo en entero. Despejar N 119. Simplificar la fracción, si es posible N = 50
|
|
|
- Víctor Luis Miguel Caballero Río
- hace 7 años
- Vistas:
Transcripción
1 .0 INTRODUCCIÓN º.0. ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NEGATIVOS -; ; 8... Decimles exctos :0,; ;... FRACCIONARIOS. Decimles periódicos puros : ;7,;... (Rcionles no enteros) ) Decimles periódicos mixtos :7,... ; - ; ; π;decimles no periódicos... º.0. PASAR DE FRACCIÓN A DECIMAL º Pr obtener l expresión deciml de un frcción, se efectú l división del numerdor entre el denomindor. º Ejemplos: 8 = Nturl 9 =, Deciml excto =,... =, ) Deciml periódico puro 7 =,... =, ) Deciml periódico mixto º.0. PASAR DE DECIMAL A FRACCIÓN º Decimles exctos: N =,8 00N = 8 8 N = 00 Multiplicr por l potenci de 0 decud pr convertirlo en entero. Despejr N 9 Simplificr l frcción, si es posible N = 0 º Decimles periódicos puros: N =, 8 00N = 8, 8 99N = N = 99 Multiplicr por l potenci de 0 decud pr obtener otro número con el mismo periodo. Restrlos (Se vn los periodos) Despejr N Simplificr l frcción, si es posible N = 99
2 º Decimles periódicos mixto: N =, 8 ) Multiplicr por l potenci de 0 decud pr convertirlo en periódico puro 0N =,8 00N = 8,8 90N = N = 90 Multiplicr por l potenci de 0 decud pr obtener otro número con el mismo periodo. Restrlos (Se vn los periodos) Despejr N Simplificr l frcción, si es posible N = 8. NÚMEROS IRRACIONALES º INTRODUCCIÓN º Números rcionles son los que se pueden poner como cociente de dos números enteros. Su expresión deciml es exct o periódic. º Números irrcionles son los no rcionles, es decir, los que no pueden obtenerse como cociente de dos números enteros. Su expresión deciml es infinit no periódic. º Hy infinitos números irrcionles, lgunos de los cules son especilmente interesntes. Vemos lguno: - L digonl del cudrdo de ldo : - Si p no es cudrdo perfecto, p es irrcionl. - En generl, si p es un número entero y n p no es un número entero (es decir, p no es un potenci n-ésim), entonces n p es irrcionl. + - L digonl de un pentágono de ldo unidd: φ = ( fi : Número áureo) - L relción entre l longitud de un circunferenci y su rdio: Π ( pi )
3 . LOS NÚMEROS REALES º.. DEFINICIÓN º El conjunto formdo por los números rcionles y los irrcionles se llm conjunto de números reles y se design por R. REALES (R) NATURALES (N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NO NATURALES -; ; 8... (Enteros negtivos) RACIONALES (Q) Decimles exctos :0,; ;... FRACCIONARIOS. Decimles periódicos puros : ;7,;... (Rcionles no enteros) ) Decimles periódicos mixtos :7,... IRRACIONALES (I) ; - ; ; π;decimles no periódicos... º Con los números reles podemos relizr ls misms operciones que hcímos con los números rcionles: sumr, restr, multiplicr y dividir (slvo por el cero) y se siguen mnteniendo ls misms propieddes. Tmbién podemos extrer ríces de culquier índice (slvo ríces de índice pr de números negtivos) y el resultdo sigue siendo un número rel. Eso no ocurrí con los números rcionles. º.. LA RECTA REAL º Si en un rect situmos un origen (el cero, 0) y mrcmos l longitud unidd, cd punto le corresponde un número rcionl o un número irrcionl. Es decir, cd punto de l rect le corresponde un número rel. Por eso, l rect numéric l llmmos rect rel. º.. REPRESENTACIÓN DE NÚMEROS SOBRE LA RECTA REAL º Todo número rel puede siturse sobre l rect rel, dependiendo de cómo se el número:
4 º Representción de nturles, enteros o decimles exctos º Ejemplo: ;, ,,,,,,,7,8,9,,,,,,,,7,8,9, º Deciml periódico: Pueden expresrse en form de frcción y representr l frcción (Se divide cd unidd en tnts prtes como teng en denomindor y se tomn tnts como teng el numerdor.) Ejemplo : 0,8.. = / 0 º Ejemplo : / = + / (Se divide igul pero l unidd entre el y el ) Ejemplo : -/ = - / (Se divide igul pero l unidd entre el y l ) º Representción de irrcionles cudráticos º Si un número irrcionl es rdicl cudrático o un combinción de ellos, se puede representr construyendo triángulos rectángulos (Se utiliz el teorem de Pitágors donde l hipotenus es lo que queremos dibujr.) ( 0 ) = +
5 º Representción de números irrcionles º Si un número irrcionl viene ddo por su expresión deciml, podemos representrlo, de form proximd: Ejemplo:, ,,,,,,,7,8,9,,,,,,,,7,8,9, Podemos finr tnto como quermos. Los números reles pueden ser representdos en l rect rel, según los csos, de form exct, o bien con tnt proximción como quermos.. INTERVALOS Y SEMIRRECTAS º Pr designr lgunos trmos de l rect rel, existe un nomencltur especil: º NOMBRE SÍMBOLO SIGNIFICADO REPRESENTACIÓN Intervlo bierto (, { x / < x < b } Nº comprendidos entre y b, sin incluir ni b Intervlo cerrdo [,b] { x / x b } Nº comprendidos entre y b, mbos incluidos. (,b] { x / < x b } Nº comprendidos entre y b, Intervlo semibierto incluido b pero no [, { x / x < b } Nº comprendidos entre y b, incluido pero no b (-,) { x / x < } Números menores que Semirrect (-,] { x / x } Nº menores que y el propio (,+ ) { x / < x } Números myores que [,+ ) { x / x } Nº myores que y el propio L propi rect rel se represent en form de intervlo, sí: R = (-,+ )
6 POTENCIAS º PROPIEDADES Y OPERACIONES CON POTENCIAS º [] 0 = [] m. n = m+n [] (. n = n.b n [8] -n = n [] = [] m : n = m-n [7](: n = n : b n n b b [9] = = n b [] ( m ) n = m.n n n. RAÍCES Y RADICALES º.. DEFINICIÓN º Se llm ríz n-ésim de un número y se escribe n, un número b que cumple l siguiente condición: n = b si b n = n se llm rdicl, rdicndo, y n, índice de l ríz. º.. ALGUNAS PECULIARIDADES DE LAS RAÍCES º Si 0, n existe culquier que se n Si < 0, sólo existe su ríz de índice impr. Aunque en generl, un número positivo,, tiene dos ríces cudrds: y -, con nos referimos su ríces positiv, es decir,. º.. FORMA EXPONENCIAL DE LOS RADICALES º Form exponencil de rdicles : n = n m = n m n º.. POTENCIAS Y RAÍCES CON CALCULADORA º Ríces cudrds: =,078 º Potencis: x y x y =,8707 9,
7 º Ríces con l tecl x y 0 8 = (8) 8 ( : ) =, = x y 0 /x =,77 º y Tecl x (En otrs clculdors x ) 0 = 0 x =, y. PROPIEDADES DE LOS RADICALES º Los rdicles tienen un serie de propieddes que se deducen de ls propieddes de ls potencis: º np p n. = n n n.. b = b n. n n = b b n n p. ( ) p = m n mn. = º. Sum o diferenci de rdicles : Dos rdicles distintos no pueden sumrse si no es obteniendo sus expresiones decimles proximds. Sólo puede sumrse rdicles idénticos. + = + = = = + + = 0 º 7. Pr multiplicr o dividir rdicles: Primero hy de reducirlos índice común. =. =. = =. 00 º 8. Rcionlizción de denomindores : A veces conviene suprimir ls ríces del denomindor. Pr ello hy que multiplicrlo por l expresión decud. Nturlmente, el numerdor tmbién se multiplicrá por es mism expresión. = =. = = = + = + = ( )
8 .7 NÚMEROS APROXIMADOS. NOTACIÓN CIENTÍFICA º 7. EXPRESIÓN APROXIMADA DE UN NÚMERO. CIFRAS SIGNIFICATIVAS. º Cundo utilizmos los números decimles pr expresr mediciones concrets, se deben dr con un cntidd decud de cifrs significtivs. º Se llmn cifrs significtivs quells con ls que se expres un número proximdo. Sólo de deben utilizr quells cuy exctitud nos conste. º Pr expresr un cntidd con un número determindo de cifrs significtivs recurriremos l redondeo, si l primer cifr que desprecimos es myor o igul que umentmos en un unidd l últim cifr significtiv y si es menor que cinco l dejmos como está. Ejemplos: Redonder con tres cifrs significtivs: Al redonder números decimles, normlmente, nos quedmos con dos decimles..7. CONTROL DEL ERROR COMETIDO º Cundo dmos un medid proximd, estmos cometiendo un error. º El Error Absoluto es l diferenci entre el Vlor Rel y el Vlor Aproximdo, en vlor bsoluto (en positivo) Error Absoluto = Vlor Rel Vlor Aproximdo El vlor excto, generlmente, es desconocido. Por tnto, tmbién se desconoce el error bsoluto. Lo importnte es poder cotrlo: el error bsoluto es menor que Un cot del error bsoluto se obtiene prtir de l últim cifr utilizd: (0, unidd de l últim cifr utilizd) º Pero no es lo mismo cometer un error de un centímetro l medir un tiz que un pizrr, por tnto definimos: El Error Reltivo como es el cociente entre el error bsoluto y el vlor rel Error Reltivo = Error Absoluto Vlor Rel Es tnto menor cuánts más cifrs significtivs se usn. º Llmmos cots de los errores cntiddes myores o igules que los errores con menor o igul número de cifrs significtivs.
9 .8 NOTACIÓN CIENTÍFICA º.8. INTRODUCCIÓN º Los números siguientes están puestos en notción científic:,8. 0 = ( cifrs prtir de l com) 7,. 0 - = 0, ( cifrs de l com l 7) º L notción científic tiene sobre l usul l siguiente ventj: ls cifrs se nos dn contds, con lo que el orden de mgnitud del número es evidente. Est notción es útil, sobre todo, pr expresr números muy grndes o muy pequeños. º.8. DEFINICIÓN º Un número puesto en notción científic const de : - Un prte enter formd por un sol cifr que no es el cero(l de ls uniddes) - El resto de ls cifrs significtivs puests como prte deciml. - Un potenci de bse 0 que d el orden de mgnitud del número. N =, bcd... x 0 n = Prte enter (sólo un cifr) bcd... = Prte deciml 0 n = Potenci enter de bse 0 º Si n es positivo, el número N es grnde Si n es negtivo, el número N es pequeño º.8. OPERACIONES CON NÚMEROS EN NOTACIÓN CIENTÍFICA º En sums y en rests hy que preprr los sumndos de modo que tengn todos l mism potenci de bse 0 y sí poder scr fctor común., ,9. 0 7,. 0 0 =, = = (, ). 0 9 = = 8, =,88. 0,8. 0 º El producto, el cociente y l potenci son inmeditos, teniendo en cuent: 0 b. 0 c = 0 b+c 0 b : 0 c = 0 b-c b b. c ( 0 ) = 0 (,. 0 ). (,. 0 8 ) = (,.,) =,0. 0 =,0. 0,. 0 (,. 0 ) : (,. 0 8 ) = (, :,). 0-8 = 0, = 8,7. 0-8,. 0 - (,. 0 ) = (,). 0. = 7,7. 0 =,77. 0,7. 0 c
10 CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8 Deciml excto, Frccionrio, Rcionl, Rel 0 = Nturl, Entero, Rcionl, Rel -, =, Deciml periódico puro, Frccionrio, Rcionl, Rel 7 Deciml no periódico, Irrcionl, Rel = Nturl, Entero, Rcionl, Rel Deciml no periódico, Irrcionl, Rel - Entero negtivo, Entero, Rcionl, Rel 7, Deciml periódico mixto, Frccionrio, Rcionl, Rel EJERCICIO : Sitú cd número en su lugr correspondiente dentro del digrm:,; ; ; 8; ; ; ;,... EJERCICIO : Represent sobre l rect los siguientes números: 7,; ;
11 EJERCICIO : Represent en l rect rel los siguientes números, utilizndo el Teorem de Pitágors: ) 0 8 ) 0 7 L hipotenus de un triángulo rectángulo de ctetos 7 y es l longitud pedid. Con el compás podemos trsldr est medid donde deseemos. 8 9 EJERCICIO : Represent en l rect rel los siguientes números, utilizndo el Teorem de Pitágors: ) 8 EJERCICIO : Represent en l rect rel: ),7, )
12 INTERVALOS Y SEMIRECTAS EJERCICIO 7 : Escribe en tods ls forms posibles los siguientes intervlos y semirrects: x / x b, c Números myores que - d, b x / x c, d [, 7] Intervlo semibierto Semirrect Semirrect Intervlo cerrdo Números comprendidos entre - y, incluido - Números menores o igules que - x / x x / x 7 Números comprendidos entre y 7, mbos incluidos FRACCIONES, POTENCIAS Y DECIMALES EJERCICIO 8 Oper y simplific el resultdo: b Simplific:, Expresmos N, en form de frcción: 00N,... 0N, N 0 N 90 Opermos y simplificmos: b EJERCICIO 9 Clcul y simplific el resultdo: b Simplific, usndo ls propieddes de ls potencis: Expresmos N 0,8 en form de frcción: 00N 8,... 0N 8, N 7 N 90 Opermos y simplificmos: 0,8 -
13 b 0 EJERCICIO 0 ) Efectú y simplific:, 9 Reduce un sol potenci: 0 ) Expresmos N, en form de frcción: 00N,... 0N, N 0 N 90 Opermos y simplificmos: : EJERCICIO Oper y simplific:, 8 b Reduce un sol potenci y clcul: Expresmos N, en form de frcción: 00N,... 0N,... : 9 90N 9 N 90 Opermos y simplificmos: b : : RAÍCES EJERCICIO : Averigu el vlor de k en cd cso: ) k 7 k c) k
14 ) k 7 7 k k 0 k k k c) k k k EJERCICIO : Expres como potenci de x y simplific. D el resultdo finl en form de ríz: ) c) x x x x x x ) x x x x 7 x x x 7 x x x x x x x x x x x x EJERCICIO : Extre del rdicl todos los fctores que se posible: ) 8 b c) x y z b c 7 ) 8 b b b b x y x y y z z z c) x x x x x x x 7 c) b c b c c EJERCICIO : Simplific y extre los fctores que pueds fuer del rdicl: ) c) ) c) 0 EJERCICIO : Expres como potenci de exponente frccionrio y simplific. D el resultdo finl en form de ríz: ) 0 c) 9 7
15 ) 0 0 / / c) 9 7 EJERCICIO 7 ) Oper y simplific: 00 Rcionliz y simplific: ) EJERCICIO 8 ) Clcul y simplific: 8 7 Rcionliz y simplific: ) EJERCICIO 9 ) Efectú y simplific: 0 8 Rcionliz y simplific: ) EJERCICIO 0 ) Oper y simplific: 8 00 Rcionliz y simplific: 8
16 ) EJERCICIO ) Efectú y simplific: Rcionliz y simplific: 8 7 ) EJERCICIO Clcul y simplific : b Rcionliz y simplific : b EJERCICIO Oper y simplific : 7 b Rcionliz y simplific : b EJERCICIO Oper y simplific: 00 b Rcionliz y simplific:
17 00 0 b 0 EJERCICIO : Clcul y simplific: ) 8 8 x x x ) x x x x x x x x x x EJERCICIO : Oper y simplific: ) 7 7 ) EJERCICIO 7 : Clcul y simplific el resultdo: ) ) EJERCICIO 8 : Oper y simplific: ) )
18 7 7 EJERCICIO 9 : Clcul y simplific: ) ) EJERCICIO 0 Simplific y extre los fctores que pueds fuer del rdicl: 9 I 7 0 II III b b Rcionliz y simplific : ) I II III b 9 b 0 b EJERCICIO : Expres como un solo rdicl: ) c) 7 7 ) c) EJERCICIO : Rcionliz y simplific: ) c) )
19 8 c) EJERCICIO : Rcionliz y simplific: ) c) ) c) EJERCICIO : Rcionliz y simplific: ) c) ) c) EJERCICIO : Rcionliz y simplific: ) 7 c) ) c) 8 7 7
20 APROXIMACIONES Y ERRORES EJERCICIO : Hll con yud de l clculdor, proximndo, cundo se necesrio, hst ls centésims: ) ) 7 8, 777 c) 7 c) 7,0 d),7 EJERCICIO 7 : Aproxim cd un de ls siguientes cntiddes, dndo dos cifrs significtivs: I Hy 7 estudintes en un instituto. II Victori pes 8, kg. b Hll el error bsoluto y el error reltivo cometidos l hcer ls proximciones. I 7 estudintes cientos de estudintes Error bsoluto Vlor rel Vlor proximdo = estudintes 7 Error _ reltivo 0,078..., II 8, kg 8 kg Error bsoluto 8, 8 0, kg 0, Error _ reltivo, ,9.0 8, EJERCICIO 8 Aproxim hst ls décims cd uno de los siguientes números: A,8 B 9,7 b Hll el error bsoluto y el error reltivo que se cometen l tomr ess proximciones. d) A,8,8 Error bsoluto Vlor rel Vlor proximdo =,8,8 0,0 0,0 Error _ reltivo 0,079...,8.0,8 B 9,7 9, Error bsoluto 9,7 9, 0,0 0,0 Error _ reltivo 0, ,.0 9,7 EJERCICIO 9 : D un cot pr el error bsoluto y otr pr el error reltivo cometidos l hcer ls siguientes proximciones: L ltur de un edificio es de metros. b En un bibliotec hy miles de libros. El error bsoluto es menor que medi unidd del orden de l últim cifr significtiv:error bsoluto Un cot pr el error reltivo es: Error reltivo Vlor proximdo
21 Por tnto: ) Error bsoluto 0, metros Error bsoluto 00 libros Error _ reltivo 0, 0,08...,.0 00 Error _ reltivo 8, ,9.0 EJERCICIO 0 Expres con un número rzonble de cifrs significtivs cd un de ls siguientes cntiddes: I 8 ejemplres vendidos de un libro. II Hemos gstdo,8 en nuestrs vcciones. b Qué error bsoluto estmos cometiendo l considerr 9 miles de hbitntes como proximción de 9 8? Y error reltivo? I 8 ejemplres 8 cientos de ejemplres II,8 cientos de b Error bsoluto Vlor rel Vlor proximdo hbitntes 8 Error _ reltivo 8, , EJERCICIO : En un librerí se hn vendido 7 ejemplres de un determindo libro,, cd uno. ) Cuánto dinero se h recuddo en l vent? Aproxim l cntidd obtenid dndo dos cifrs significtivs. Di cuál es el error bsoluto y cuál el error reltivo cometidos l hcer l proximción. ) 7, 7 0,9 7 decens de miles de Error bsoluto Vlor rel Vlor proximdo 7 0, ,9 0,9 Error _ reltivo,0...0,.0 70,9 NOTACIÓN CIENTÍFICA EJERCICIO Escribe en form deciml estos números: A, 0 B, 0 8 b Expres en notción científic ls siguientes cntiddes: C D 0, E A B 0, b C, 0 D 0 8 E 8, 0 EJERCICIO Al relizr con l clculdor l operción 0 hemos obtenido en l pntll lo siguiente: Expres en notción científic el número nterior. De cuánts cifrs es dicho número? b Aproxim el resultdo nterior dndo tres cifrs significtivs. D un cot pr el error bsoluto y otr pr el error reltivo cometidos l hcer l proximción.,089 0 Tiene cifrs
22 b Aproximción,0 0 Error bsoluto 0 0 Error reltivo 0, <,.0 - Vlor proximdo,0 0 EJERCICIO Si clculmos 0 con l clculdor, obtenemos en pntll: Expres el número nterior en notción científic y en form deciml. b Aproxim el resultdo nterior dndo dos cifrs significtivs. D un cot pr el error bsoluto y otr pr el error reltivo cometidos l hcer l proximción. 9,7 0 7 Notción científic 0, Notción deciml b Aproximción 9, 0 7 Error bsoluto Error reltivo 0,00. <,7.0-7 Vlor proximdo 9, 0 EJERCICIO : Clcul, expresndo el resultdo en notción científic con tres cifrs significtivs: ) c) I) I) I),8 0 8, II), 0 7,8 0, 0 8, 0, , 0, 0 0 II), 0 9, 0 8, 0 0 II), 0 8,0 0 9, 0 7,8 0 8,0 9,8, 0 7, ) I) 7,09 0 7, II), 0 7,8 0, 0 8 0, , , 0,9 0 8,9 0 8, 0,80,,8 0 9,0 0 ) I),80 0, II), 0 9, 0 8, 0 0, 0 8, ,, 0 8 8, 0 8,8 0 0, , 0,0 8,, 0 8,7 0 ) I), 0, II), 0 8,0 0 9, 0 7, , 0 7, 0, 0 7,79 0 7,79 0 9, 0 9 EJERCICIO : Ddos los números: A, 0 8 B,0 0 7 C 0 9
23 Efectú ls siguientes operciones, dndo el resultdo en notción científic con dos cifrs significtivs: I) A B C II) A B C 8 7, 0,0 0,,0 0,79 0 ) I) 7, , II), 0 8, , 0 7, ,, ,8 0 7,8 0 9, 0 9 EJERCICIO 7 ) Hll, con yud de l clculdor, el resultdo de ests operciones en notción científic con tres 8, 7 0, 0 cifrs significtivs:, 0, 0 D un cot pr el error bsoluto y otr pr el error reltivo cometidos l dr el resultdo proximdo. ) (.7 EXP 8. EXP ) (. EXP. EXP ) Por tnto: Error bsoluto 0,7 0, 0, 0, 0 8,9 0 Error reltivo Error reltivo 0,00 Vlor rel Vlor proximdo EJERCICIO 8 ) Hll, con yud de l clculdor, dndo el resultdo en notción científic con tres cifrs 9 8, 8 0, 0 significtivs:, 0, 0 D un cot pr el error bsoluto y otr pr el error reltivo cometidos l dr el resultdo proximdo. ) (.8 EXP 9. EXP 8 ) (. EXP /. EXP / ) ,8 0, 0, 0, Por tnto: Error bsoluto 0 7, 0 Error reltivo Error reltivo 0,000. <, 0 - Vlor rel Vlor proximdo EJERCICIO 9 : L velocidd de l luz, en el vcío, es km/s. Cuántos metros recorre l luz en un dí?. Expres el resultdo en notción científic. 8 dí =00=8.00 s e 0 8,0 =,90 m. 0
24 EJERCICIO 0 :Un determind bcteri mide.0 - m. Cuánts bcteris colocds en líne rect serín necesris pr cubrir metro de longitud? x 0 =0, bcteris. EJERCICIO : El diámetro de l lun es de 00 Km., proximdmente, cuánto tiempo trdrí en dr un vuelt complet un stélite cuy órbit se encuentr 00 Km. de l superficie lunr, si su velocidd medi es de m./h? L LUNA= r = 90 =, 0 Km =, 0 7 m. t =, 0 v e 0, 0 hors = hors, 8 minutos y segundos proximdmente. EJERCICIO : Un virus se duplic cd minutos. Podrís decir cuántos virus hbrá l cbo de un hor?, y de un dí? Inicio: virus A los min. : = virus A los min.: = virus... A los 0 min. 0 =, virus EJERCICIO : Sbemos que un ño luz equivle 9,.0 Km. Si l distnci de l Tierr Andrómed son,.0 ños luz. Cuántos kilómetros son l distnci que nos sepr de Andrómed? 9, 0, 0, Km. CALCULADORA EJERCICIO : Hll, con yud de l clculdor:, 0, 0, b 7 (, EXP 8, EXP 7 ), EXP / Por tnto:, 0, 0, , 0 b 7.x y ( ) Por tnto: 7,0 9 EJERCICIO : Utiliz l clculdor pr hllr el resultdo de ests operciones:, 0, 0, 0 0 b
25 (, EXP /, EXP / ) x, EXP Por tnto:, 0, 0, 0 0,0 0 8 b ( ) Por tnto: EJERCICIO : Hll, con yud de l clculdor:,,9 0, 0, b (,9 EXP 9, EXP 0 ), EXP /..078 Por tnto:,9 0, 0, 0 9 0, 0 b.x /y.88.. Por tnto:, EJERCICIO 7 : Utiliz l clculdor pr obtener el resultdo de ests operciones:,0 0, (,0 EXP /, EXP 7 / ) EXP Por tnto:,0 0, ,0 0 b ( X ) Por tnto:,99 EJERCICIO 8 : Hll con yud de l clculdor:,8 0, 0, 0 b (,8 EXP, EXP ), EXP /... Por tnto:,8 0, 0, 0 b x y.(..87., 0 Por tnto:,
26 CUESTIONES EJERCICIO 9 : Rzon si ls siguientes igulddes son verdders o flss: ) c) d) : 0 ) Flso, l expresión no puede ser reducid un único sumndo. c) Verddero. -(-) d) Flso, : = =. 0 Verddero, = =. EJERCICIO 0 : Rzon si ls siguientes igulddes son verdders o flss: b b ) b b b +b ) Flso, =. b b b d) Verddero, =. c) b b Flso. c) Verddero. b b d)
27 Clsificción y representción gráfic de números reles EJERCICIO : Represent sobre l rect rel los siguientes números y clsifíclos ) c) 0 d) 9/ e) / f) 8/ g) / EJERCICIO : Orden de myor menor los siguientes números, sócilos los conjuntos de números que correspond (N, Z, Q, R) y represéntlos: ; 0; -; 0,; -0,; ; ; -/; 7 ; -,;, ;,... ; 9 ; 7 Operciones con números decimles. Pso frcción genertriz EJERCICIO : Obtén el siguiente vlor en términos de frcción: ).(,, , x ) 0,... = EJERCICIO : Clcul: ) 0,.0, 0,ˆ 0, +, 0, Intervlos y semirrects EJERCICIO : Describe, en tods ls forms posibles: ) Intervlo bierto de extremos y [-,0) c) {x R / - < x } d) Números myores que e) (-, ] f) Potencis y ríces EJERCICIO : Escribe en form de un sol potenci: ) [( ) 7 : ( ) ] 0.( ) [(-) ].[(-) ] c) [(x-) - ] : [(x-) - ] d) (. ) : (. 7 ) e) ( ) : (.. ) f) [(+) : (+) - ] EJERCICIO 7 : Expres, en términos de ríces, ls siguientes expresiones: ) / 7 -/ c) (/) /7 d) (/) -/ EJERCICIO 8 : Agrup bjo un rdicl único: ). 7 : c). d) : e) /. / f) / x. x / EJERCICIO 9 : Extre todos los fctores que pueds de los siguientes rdicles: )...b 7.. b c) d). EJERCICIO 0 : Introducir en los rdicles los fctores que están fuer de ellos: )..b.. b c) 7.. d).b. b EJERCICIO : Clcul: ) c) d) e) f) EJERCICIO : Clcul: ) c)
28 d) e). / +. / + / 7 f) 80. EJERCICIO : Simplific: ) e). /. / c) 8. f) /. /. / g). d). x /. EJERCICIO : Rcionliz: ). 7 e) 7 i) f) j).. c) g) k) 7 d) h) l).... x y Errores y cots EJERCICIO : Hll ls cots del error bsoluto y del error reltivo l sustituir por, EJERCICIO : Se proxim el número 0, medinte redondeo, en ls milésims. Clcul el error reltivo de est proximción. EJERCICIO 7 : Si el resultdo de un medid es, con un error de 0,0, entre qué vlores se encuentr l medid exct? EJERCICIO 8 : El presupuesto de un reprción es de 00 euros con error posible del %. Entre qué vlores puede oscilr est reprción? EJERCICIO 9 : Al indicr el número de lumnos de un instituto se comete un error de lumnos. Si relmente hy 0 lumnos. Qué número se dio? Cuál es el error reltivo cometido?. Notción científic EJERCICIO 0 : Escribe en notción científic los siguientes números: ) c) d) 0, e) 7898, f) 0, g) 0, h) 0, EJERCICIO : Oper: ) (7,.0-7 ).(,0.0 ),0.0,0.0 c) (,0.0 0 ).(.0 9 ) d) e) 0,00 +,.0 - f),.0 - +, ,0.0 - EJERCICIO : Efectú en notción científic ls siguientes operciones, dndo el resultdo en notción científic con tres cifrs significtivs:,.0 7,8.0.(,.0 ),.0 7, ,.0 ),8.0,.0,.0,.0 c) 8,.0.0 9,8.0,.0, d).0,.0
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN:
 TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
Números racionales son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresar en forma de fracción.
 MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
LITERATURA Y MATEMÁTICAS. El código Da Vinci
 Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
3. Expresa los siguientes radicales mediante potencias de exponente fraccionario y simplifica: 625 d) 0, 25 e) c) ( ) 4 8
 POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
LÁMINA No. 1.1 LECTURA Y ESCRITURA DE UN NÚMERO
 6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
Los números enteros y racionales
 Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Respuesta: Con este resultado Anahí decide contratar a estos pintores.
 Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
TEMA 1. NÚMEROS REALES
 TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
Inecuaciones con valor absoluto
 Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
(lo podemos visualizar como el área de un cuadrado de lado 4) Pues bien, diremos que la base de dicha potencia, 4, es su raíz cuadrada exacta: 16 = 4.
 Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
Ejemplo: Para indicar el conjunto (que llamaremos M), formado por los números 4, 6 y 8, escribimos: M = { 4, 6, 8}
 NÚMEROS REALES. BREVE REPASO DE LA TEORÍA DE CONJUNTOS En est unidd utilizremos ls notciones l terminologí de conjuntos. L ide de conjunto se emple mucho en mtemátic se trt de un concepto básico del que
NÚMEROS REALES. BREVE REPASO DE LA TEORÍA DE CONJUNTOS En est unidd utilizremos ls notciones l terminologí de conjuntos. L ide de conjunto se emple mucho en mtemátic se trt de un concepto básico del que
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
NÚMEROS RACIONALES. Los números racionales son todos aquellos números de la forma b
 NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
EJERCICIOS DE RAÍCES
 EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Presentación Axiomática de los Números Reales
 Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
FUNCIONES. Analíticamente, la correspondencia anterior se escribe del modo siguiente:
 FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
pág. 71 LIMITES 1. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerda del curso pasado los límites de sucesiones.
 LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
OPERACIONES CON RADICALES
 OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
1. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN
 http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 3 1. NÚMEROS RACIONALES UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números
C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 3 1. NÚMEROS RACIONALES UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números
LA FUNCIÓN LOGARÍTMICA
 LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
Repaso de Matemática Básica
 Addison-Wesley s Repso de Mtemátic Básic Números Propieddes Importntes NÚMEROS NATURALES NÚMEROS ENTEROS NO NEGATIVOS {, 2, 3, 4, 5, } {0,, 2, 3, 4, } NÚMEROS ENTEROS {, 3, 2,, 0,, 2, } Rect Numéric 5
Addison-Wesley s Repso de Mtemátic Básic Números Propieddes Importntes NÚMEROS NATURALES NÚMEROS ENTEROS NO NEGATIVOS {, 2, 3, 4, 5, } {0,, 2, 3, 4, } NÚMEROS ENTEROS {, 3, 2,, 0,, 2, } Rect Numéric 5
1 Agrupa aquellos monomios de los que siguen que sean semejantes, y halla su suma: , cuando:
 Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
3º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa NÚMEROS REALES
 º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1. conjunto de todos ellos se les designa con la letra Q.
 Matemáticas B º E.S.O. Tema 1 Los números Reales 1 TEMA 1 LOS NÚMEROS REALES 1.1 CLASIFICACIÓN DE LOS NÚMEROS REALES º 1.1.1 TIPOS DE NÚMEROS º Los números naturales son : 1, 2,,..., 10, 11,..., 102, 10,....
Matemáticas B º E.S.O. Tema 1 Los números Reales 1 TEMA 1 LOS NÚMEROS REALES 1.1 CLASIFICACIÓN DE LOS NÚMEROS REALES º 1.1.1 TIPOS DE NÚMEROS º Los números naturales son : 1, 2,,..., 10, 11,..., 102, 10,....
OPERACIONES CON FRACIONES
 LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
pág. 87 LIMITES 1. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerda del curso pasado los límites de sucesiones.
 LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 + + + + 4 4 n n + es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de
LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 + + + + 4 4 n n + es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de
REPASO DE ECUACIONES (4º ESO)
 TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
LÍMITES CONCEPTO INTUITIVO DE LÍMITE
 Mrí Teres Szostk Ingenierí Comercil Mtemátic II Clse Nº, LÍMITES El concepto de ite, es uno de los pilres en que se bs el Análisis Mtemático, se encontrb en 8 en estdo potencil, ern más principios intuitivos
Mrí Teres Szostk Ingenierí Comercil Mtemátic II Clse Nº, LÍMITES El concepto de ite, es uno de los pilres en que se bs el Análisis Mtemático, se encontrb en 8 en estdo potencil, ern más principios intuitivos
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
Ejercicios Tema 1. a) b) c) d) e) f) Ejercicio 6. Escribe en forma de intervalo y representa:
 Ejercicios Tema 1 Números Reales Ejercicio 1. Clasifica los siguientes números en el lugar que conjunto que corresponde: a) b) c) Ejercicio 2. Clasifica los siguientes números: Ejercicio 3. a) Cuáles de
Ejercicios Tema 1 Números Reales Ejercicio 1. Clasifica los siguientes números en el lugar que conjunto que corresponde: a) b) c) Ejercicio 2. Clasifica los siguientes números: Ejercicio 3. a) Cuáles de
Las matemáticas son una ciencia experimental que basa su desarrollo en la intuición y la lógica.
 L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
Guía de Trabajo n 1 Octavo año básico Refuerzo Contenido y Aprendizaje N. Cero (restitución de aprendizajes) Números
 Colegio Antil Mwid Deprtmento de Mtemátic Profesor: Nthlie Sepúlved Guí de Trjo n Octvo ño ásico Refuerzo Contenido y Aprendizje N Fech Tiempo 2 Hors Nomre del/l lumno/ Unidd Nº Núcleos temáticos de l
Colegio Antil Mwid Deprtmento de Mtemátic Profesor: Nthlie Sepúlved Guí de Trjo n Octvo ño ásico Refuerzo Contenido y Aprendizje N Fech Tiempo 2 Hors Nomre del/l lumno/ Unidd Nº Núcleos temáticos de l
El conjunto de los números reales se forma mediante la unión del conjunto de los números racionales y el conjunto de los números irracionales.
 El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
1 Halla las razones trigonométricas del ángulo a en cada uno de estos triángulos: a) b) c)
 Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
Se desea calcular la longitud de un lado de una pista de baile de forma cuadrada, cuya área es 16 u 2. Sustituyendo el valor del área
 Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
11 Perímetros y áreas de figuras planas
 86464 _ 0371-0384.qxd 1//07 09:4 Págin 371 Perímetros y áres de figurs plns INTRODUCCIÓN En est unidd repsmos ls uniddes de longitud y superficie. Se introducen tmbién lguns uniddes de medid del sistem
86464 _ 0371-0384.qxd 1//07 09:4 Págin 371 Perímetros y áres de figurs plns INTRODUCCIÓN En est unidd repsmos ls uniddes de longitud y superficie. Se introducen tmbién lguns uniddes de medid del sistem
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
Las matemáticas son una ciencia experimental que basa su desarrollo en la intuición y la lógica.
 L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
CENTRO DE FORMACIÓN PROFESIONAL. REVILLAGIGEDO Jesuitas - Gijón JOSÉ MANUEL FERNÁNDEZ GARCÍA
 CENTRO DE FORACIÓN PROFESIONAL REVILLAGIGEDO Jesuits - Gijón PRONTUARIO DE ATEÁTICAS PARA ELECTRÓNICOS Y ELÉCTRICOS JOSÉ ANUEL FERNÁNDEZ GARCÍA CÁLCULO NUÉRICO. Redondeo. Dependiendo de ls mgnitudes con
CENTRO DE FORACIÓN PROFESIONAL REVILLAGIGEDO Jesuits - Gijón PRONTUARIO DE ATEÁTICAS PARA ELECTRÓNICOS Y ELÉCTRICOS JOSÉ ANUEL FERNÁNDEZ GARCÍA CÁLCULO NUÉRICO. Redondeo. Dependiendo de ls mgnitudes con
Se llama logaritmo en base a de P, y se escribe log a P, al exponente al que hay que elevar la base a para obtener P.
 Log P X Se llm ritmo en bse de P, y se escribe P, l eponente l que hy que elevr l bse pr obtener P. Log P P Ejemplo: 8 8 L l it b d 8 Leemos, ritmo en bse de 8 es porque elevdo es 8. Anámente podemos decir:
Log P X Se llm ritmo en bse de P, y se escribe P, l eponente l que hy que elevr l bse pr obtener P. Log P P Ejemplo: 8 8 L l it b d 8 Leemos, ritmo en bse de 8 es porque elevdo es 8. Anámente podemos decir:
Propiedades de la Potencia. Observación: La potencia no es distributiva con respecto a la suma ni a la resta.
 Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
( ) 4. Colegio Diocesano Sagrado Corazón de Jesús. MATEMÁTICAS I / 1º Bachillerato C y T LOGARTIMOS. log. log. log. 1 log log 3.
 Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Formalización de los Números Reales. M. en I. Gerardo Avilés Rosas
 Formlizción de los Números Reles M. en I. Gerrdo Avilés Ross Agosto de 016 Tem Formlizción de los Números Reles Objetivo: El lumno plicrá ls propieddes de los números reles y sus subconjuntos, pr demostrr
Formlizción de los Números Reles M. en I. Gerrdo Avilés Ross Agosto de 016 Tem Formlizción de los Números Reles Objetivo: El lumno plicrá ls propieddes de los números reles y sus subconjuntos, pr demostrr
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidd de Cádiz Deprtmento de Mtemátics MATEMÁTICAS pr estudintes de primer curso de fcultdes y escuels técnics Tem 1 Nociones mtemátics básics. Los números. Operciones Elbordo por l Profesor Doctor
Universidd de Cádiz Deprtmento de Mtemátics MATEMÁTICAS pr estudintes de primer curso de fcultdes y escuels técnics Tem 1 Nociones mtemátics básics. Los números. Operciones Elbordo por l Profesor Doctor
CURSO DE NIVELACIÓN 2012 EJERCITARIO TEÓRICO DE MATEMÁTICA I
 CURSO DE NIVELACIÓN 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I. Con relción l potencición, se firm que es un operción: ) Conmuttiv. ) Distriutiv respecto l sum. 3) Distriutiv
CURSO DE NIVELACIÓN 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I. Con relción l potencición, se firm que es un operción: ) Conmuttiv. ) Distriutiv respecto l sum. 3) Distriutiv
MATEMÁTICAS PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 25 AÑOS LOGARITMOS
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
LÍMITES DE FUNCIONES
 LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
1. Cuales son los números naturales?
 Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Máximo común divisor. 2. Descomposición en primos Ejemplo. Encontrar mcd 504,300 Se descomponen ambos números en primos 504 2 252 2 126 2 63 3 21 3
 Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
TEMA 1: FUNCIONES. LÍMITES Y CONTINUIDAD
 Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
Ejercicios de números reales
 Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Resolver inecuaciones como las siguientes. Expresar la solución en forma gráfica y algebraica. Comparar las soluciones de los ejercicios e), f) y g).
 64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
TEMA 3: PROPORCIONALIDAD Y PORCENTAJES.
 TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
Actividades propuestas
 Cpítulo 1: Números reles TEORÍA. Mtemátics º de ESO En este primer cpítulo vmos repsr muchs coss que y conoces, como ls operciones con los números, representr los números en un rect, ls potencis Si todo
Cpítulo 1: Números reles TEORÍA. Mtemátics º de ESO En este primer cpítulo vmos repsr muchs coss que y conoces, como ls operciones con los números, representr los números en un rect, ls potencis Si todo
NÚMEROS COMPLEJOS. Números reales Intervalos El conjunto R 2 Discos Números complejos Teorema fundamental del Álgebra
 NÚMEROS COMPLEJOS Números reles Intervlos El conjunto R 2 Discos Números complejos Teorem fundmentl del Álgebr NÚMEROS REALES Números nturles, enteros rcionles e irrcionles En mtemátics son importntes
NÚMEROS COMPLEJOS Números reles Intervlos El conjunto R 2 Discos Números complejos Teorem fundmentl del Álgebr NÚMEROS REALES Números nturles, enteros rcionles e irrcionles En mtemátics son importntes
UNIDAD DIDÁCTICA 4: LOGARITMOS
 Tem 4 UNIDAD DIDÁCTICA 4: LOGARITMOS 1. ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función rítmic ritmos 4. Ecuciones eponenciles rítmics 2. INTRODUCCIÓN GENERAL A LA UNIDAD Y ORIENTACIONES
Tem 4 UNIDAD DIDÁCTICA 4: LOGARITMOS 1. ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función rítmic ritmos 4. Ecuciones eponenciles rítmics 2. INTRODUCCIÓN GENERAL A LA UNIDAD Y ORIENTACIONES
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
NÚMEROS RACIONALES ABSOLUTOS
 NÚMEROS RACIONALES ABSOLUTOS Frcción: es un pr ordendo de números nturles con l segund componente distint de cero. (, ) pr ordendo frcción es un frcción N N EQUIVALENCIA DE FRACCIONES * Frcciones diferentes,
NÚMEROS RACIONALES ABSOLUTOS Frcción: es un pr ordendo de números nturles con l segund componente distint de cero. (, ) pr ordendo frcción es un frcción N N EQUIVALENCIA DE FRACCIONES * Frcciones diferentes,
Tutorial MT-m3. Matemática Tutorial Nivel Medio. Función cuadrática
 12345678901234567890 M te m átic Tutoril MT-m3 Mtemátic 2006 Tutoril Nivel Medio Función cudrátic Mtemátic 2006 Tutoril Función Cudrátic Mrco Teórico 1. Función cudrátic: Está representd por: y = x 2 +
12345678901234567890 M te m átic Tutoril MT-m3 Mtemátic 2006 Tutoril Nivel Medio Función cudrátic Mtemátic 2006 Tutoril Función Cudrátic Mrco Teórico 1. Función cudrátic: Está representd por: y = x 2 +
O(0, 0) verifican que. Por tanto,
 Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES 2º PARCIAL
 Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
INTEGRACIÓN. CÁLCULO DE
 Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
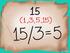 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
4. NÚMEROS REALES. José Gallegos Fernández 49. irreducible 2 = = hemos simplificado la fracción hasta llegar a 2,
 4. NÚMEROS REALES. 4.1. Introducción. En l époc de Pitágors, se creí que los únicos números que existín ern los nturles (los que emplemos pr contr) y los rcionles (frcciones). Sin embrgo, los pitgóricos
4. NÚMEROS REALES. 4.1. Introducción. En l époc de Pitágors, se creí que los únicos números que existín ern los nturles (los que emplemos pr contr) y los rcionles (frcciones). Sin embrgo, los pitgóricos
Integral de Riemann. Introducción a la integración numérica.
 Cálculo Mtemático (Práctics) M. I. Berenguer Mldondo mribel@ugr.es. 1 Integrl de Riemnn. Introducción l integrción numéric. En est práctic usremos l clculdor ClssPd pr trtr el problem de integrción. Se
Cálculo Mtemático (Práctics) M. I. Berenguer Mldondo mribel@ugr.es. 1 Integrl de Riemnn. Introducción l integrción numéric. En est práctic usremos l clculdor ClssPd pr trtr el problem de integrción. Se
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
Manual de teoría: Álgebra Matemática Bachillerato
 Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
OPERACIONES CON RADICALES
 OPERACIONES CON RADICALES Como consecuenci de ls fórmuls fundmentles de rdicles, se pueden relizr ls siguientes operciones. Se requiere que en los rdicles sólo h productos o cocientes. Si huier sumndos
OPERACIONES CON RADICALES Como consecuenci de ls fórmuls fundmentles de rdicles, se pueden relizr ls siguientes operciones. Se requiere que en los rdicles sólo h productos o cocientes. Si huier sumndos
CURSO DE MATEMÁTICA 1. Facultad de Ciencias
 CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
Taller de Matemáticas I
 Tller de Mtemátics I Semn y Tller de Mtemátics I Universidd CNCI de México Tller de Mtemátics I Semn y Temrio. Los números positivos.. Representción de números positivos... Frcciones... Decimles... Porcentjes..4.
Tller de Mtemátics I Semn y Tller de Mtemátics I Universidd CNCI de México Tller de Mtemátics I Semn y Temrio. Los números positivos.. Representción de números positivos... Frcciones... Decimles... Porcentjes..4.
open green road Guía Matemática FRACCIONES ALGEBRAICAS profesor: Nicolás Melgarejo .co
 Guí Mtemátic FRACCIONES ALGEBRAICAS profesor: Nicolás Melgrejo.co . Introducción El mnejo lgebrico es un herrmient básic que nos permite comunicr ides en el mbiente científico sin importr l lengu que ellos
Guí Mtemátic FRACCIONES ALGEBRAICAS profesor: Nicolás Melgrejo.co . Introducción El mnejo lgebrico es un herrmient básic que nos permite comunicr ides en el mbiente científico sin importr l lengu que ellos
Sistema de los Números Reales
 Sistem de los Números Reles El Conjunto de los Números Rcionles Ysel Ocho Tpi Ysel Ocho Tpi Sistem de los Números Reles /2 Introducción Los rcionles: Q Los números rcionles permiten expresr medids. Cundo
Sistem de los Números Reles El Conjunto de los Números Rcionles Ysel Ocho Tpi Ysel Ocho Tpi Sistem de los Números Reles /2 Introducción Los rcionles: Q Los números rcionles permiten expresr medids. Cundo
